简读 || A Belief Propagation Algorithm for Multipath-Based SLAM

原文链接：A Belief Propagation Algorithm for Multipath-Based SLAM | IEEE Journals & Magazine | IEEE Xplore

开源代码：https://www2.spsc.tugraz.at/people/eriklei/BP-SLAM/

 

 

摘要：文章提出了一种基于无线电信号和几何镜面多路径分量 (MPC)的SLAM算法。本文的方法，平面上的镜面反射是根据虚拟锚点 (VA) 来描述的，虚拟锚点是物理锚点 (PA) 关于反射面的镜像。这些 VA 的位置以及可能还有 PA 的位置是未知的。本文开发了 SLAM 问题的贝叶斯模型，并用因子图表示它，这使得可以使用置信传播 (BP) 来有效地边缘化联合后验分布。由此产生的基于 BP 的 SLAM 算法检测与 PA 关联的 VA，并联合估计移动代理的时变位置和 VA 的位置，可能还有 PA 的位置，从而利用无线电信号中的 MPC 来提高准确性和代理本地化的稳健性。该算法具有较低的计算复杂度，并且在所有相关系统参数中都具有良好的可扩展性。使用合成测量和真实超宽带无线电信号的实验结果证明了该算法在具有挑战性的室内环境中的出色性能。

 

关键词：SLAM、多路径通道、数据关联、因子图、消息传递、和积算法。

 

1、介绍

        SLAM是估计移动代理和周围环境的地图，来自一个或多个传感器提供的测量值。 SLAM 在许多领域都很重要，包括机器人技术 [1]、自动驾驶 [3]、位置感知通信 [4] 和稳健的室内定位 [5]-[9]。在以严酷的多径信道条件为特征的室内环境中，稳健地达到所需的精度水平仍然难以实现。因此，大多数支持多径信道的现有系统要么使用减轻多径效应的传感技术 [10]，要么融合多个信息源 [11]、[12]。

        在多径辅助室内定位 [5]、[8]、[9]、[13]-[16] 中，多径分量 (MPC) 与局部几何结构的关系可能将多径传播从损害转变为优势。本文提出了一种基于无线电信号的鲁棒室内定位 SLAM 算法。无线电信号从移动代理传输到基站，基站称为物理锚点 (PA)。由镜面反射引起的 MPC 由虚拟锚点 (VA) 建模，虚拟锚点是 PA 的镜像 [17]。本文的算法检测PA 及与之关联的 VA，并估计 VA 以及可能的 PA 位置以及移动代理的时变位置。该算法旨在应对恶劣的多径信道条件，这些条件往往会导致测量出现大量误报和漏检。虽然 MPC 可以由各种传播现象（例如镜面反射、散射和衍射）生成，但我们的模型侧重于与 PA/VA 相关的 MPC；所有其他 MPC 都被建模为干扰，即使它们包含几何信息。我们注意到在 [13] 中使用的特征模型中考虑了与散点相关的 MPC。

 

A. 基于特征的SLAM

        文章所提出的算法遵循基于特征的 SLAM 方法 [2]、[18]、[19]。该地图由具有未知空间位置的未知数量的特征表示，其状态以顺序（时间递归）方式估计。在本文的模型中，特征由 PAs 和 VAs 给出。突出的基于特征的 SLAM 算法包括：扩展卡尔曼滤波器 SLAM（EKF-SLAM）[18]，Rao-Blackwellized（RB）-SLAM（称为 FastSLAM）[2]，[13]，[20]，基于变分推理的 SLAM [21] ]、[22] 和基于集合的 SLAM [19]、[23]、[24]。最近，引入了利用无线电信号中的位置相关信息的基于特征的 SLAM 方法 [13]、[15]、[16]、[25]-[27]。这些方法中的大多数都对与 MPC 相关的估计参数进行操作。距离、到达角 (AoAs) 或出发角 (AoDs) [28]–[32]。这些参数是在预处理阶段从信号中估计出来的，并被 SLAM 方法视为“测量”。一个重要方面是这些测量值与 PAs 或 VAs 之间的数据关联 (DA)。

        基于特征的 SLAM 与多目标跟踪 (MTT) 密切相关，MTT 方法已经适用于基于特征的 SLAM [19]、[23]、[33]。适用于 SLAM 的 MTT 方法包括联合概率 DA (JPDA) 滤波器 [34] 和联合集成概率 DA (JIPDA) 滤波器 [35]。 [36]、[37] 中介绍的方法采用了类似于 JIPDA 过滤器的方法。最近，在 [40] 中的 MTT 和 [41]-[43] 中的多传感器 MTT 中引入了置信传播 (BP) [38]、[39] 的概率 DA。特别是，[41]-[43] 中的 BP 算法基于多传感器 MTT 问题的因子图表示，并且计算复杂度仅在对象（目标）数量上成二次方，在传感器数量上线性增加。 [41]、[44]、[45] 中介绍了基于随机有限集并嵌入概率 DA 的 BP 算法的 MTT 方法。最后注意到，本文基于特征的 SLAM 方法也与使用贝叶斯方法 [46] 的不确定传感器位置的多传感器目标跟踪有关。

 

B. 论文的贡献和结构

        文章提出了一种基于 BP 的贝叶斯检测和估计算法，用于使用无线电信号的 SLAM。我们的算法联合执行概率 DA 和顺序估计移动代理的状态和表征地图的“潜在特征”（PF）。我们对特征存在使用概率模型，其中每个 PF 状态都由二进制存在变量增强并与存在概率相关联，这也是估计的。所提出的算法受到[42]中提出的用于多传感器MTT的BP算法的启发，因此将简称为BP-SLAM算法。通过在代表 SLAM 问题的统计结构的因子图 [38]、[39] 上运行 BP 来执行概率 DA 和状态估计。 BP 方法利用条件统计独立性来实现低复杂性和高可扩展性。事实上，与 EKF-SLAM 和 RB-SLAM 等传统 SLAM 算法相比，所提出的 BP-SLAM 算法假设在每个时间步中代理状态和所有特征状态都是先验独立的。

        DA 概率模型和特征存在不确定性允许 BP-SLAM 算法在特别具有挑战性的仅范围 SLAM 问题 [47] 中取得成功，这不能通过已建立的 SLAM 技术 [1]，[2] 直接解决。仅从距离测量执行 SLAM 具有挑战性，因为（i）当初始化新特征时，PAs/VAs 的概率分布呈环形，因此不能很好地用高斯分布表示； (ii) 与机器人技术中的经典 SLAM 问题相比，DA 更加困难，因为在不同位置的 PA/VA 可以生成几乎相同的距离测量值。特别地，[47]的算法是能够处理仅范围测量模型，但不能处理 DA 不确定性。所提出的算法——连同[33]中提出的初步版本——是第一个用于基于特征的 SLAM 和概率 DA 的 BP 算法，它也适用于基于范围的 SLAM。

        本文的主要创新贡献包括：

• 为基于特征的 SLAM 建立贝叶斯模型，该模型使用从无线电信号中提取的 MPC 参数作为输入测量值，并对 P As/VAs 的出现和消失以及 DA 不确定性进行概率建模。

 

• 基于该模型的因子图表示，我们开发了一种可扩展的 BP 算法，用于估计移动代理的状态以及 PA/VA 的数量和位置。

 

• 我们评估所提出的算法在合成数据和真实数据上的性能。我们的实验结果证明了该算法的高精度和鲁棒性。

 

        将提出的 BP-SLAM 算法应用于具有挑战性的仅范围测量模型设置。然而，方位信息（MPC 的 AoA 和 AoD）或来自惯性测量单元传感器的信息可以很容易地合并到 BP-SLAM 算法中，这将带来显着的性能增益。为简单起见，我们假设 PA 和移动代理之间的时间同步。然而，BP-SLAM 算法可以沿着 [13] 的思路扩展到非同步 PA-agent 链接（基于相关几何信息也包含在 MPC [14]、[48] 的时间差中这一事实）或按照 [49] 的方式联合 SLAM 和同步。此外，我们假设初步信号分析阶段（产生测量）检测无线电信号特征的概率是已知的；然而，可以按照 [33]、[43]、[50] 的思路获得对未知和时变检测概率的自适应扩展。

        本文优于会议论文 [33]，因为它通过改进的贝叶斯技术取代了其中用于确定新 PF 初始分布的启发式方法。此外，[33] 的因子图和 BP 算法通过引入“新 PF”得到扩展，即首次生成测量值的特征。

        本文的其余部分安排如下。第二部分考虑了接收到的无线电信号和 MPC 参数。第三部分描述了系统模型并提供了 SLAM 问题的统计公式。状态的联合后验分布和相应的因子图在第四节中导出。在第五节中，提出了所提出的 BP-SLAM 算法。第六节报告了数值实验的结果。第七节总结了本文。

 

2、无线电信号和 MPC 参数

        基于无线电信号的 SLAM [5]、[13]、[25]、[26] 将根据接收信号估计的镜面 MPC 参数与“几何预期”参数相关联，例如距离（与延迟相关）、AoA 和 AoD。这些参数是根据移动代理和 PAs 或 VAs 的位置建模。 VA 位置是 PA 位置的镜像，由平面（通常是墙壁）的反射引起，因此取决于周围环境（平面图）[17]。对于每个反射路径，从 PA（通过平面）到移动代理的长度等于从 VA 到移动代理的长度。即使移动代理移动，只要 PA 和平面（平面图）是静态的，VA 就会保持静态。请注意，VA 位置未知，因为平面图未知。例如，图 1 描绘了一个平面图，其中包含两个 PA 和一些相应的一阶 VA，以及一个属于一些较大平面的二阶 VA。还显示了移动代理位置 p350 的三个反射路径（对于两个 PA）。 [51, Ch.2] 中描述了高阶 VAs 的构造。

 

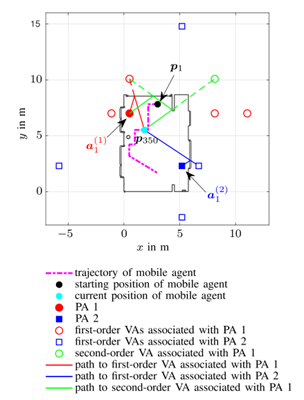
图1

 

 

3、系统模型和统计公式

A. 代理状态和 PF 状态

 

B.关联向量

 

C.先验概率

 

D.似然函数

 

四、联合后验PDF和因子图

A.排除约束的冗余公式

 

B.联合后验pdf

 

 

 

 

 

 

 

五、BP-SLAM 算法

        所提出的 BP-SLAM 算法执行相关状态的贝叶斯检测和估计。通过在图 2 中的因子图上使用 BP 消息传递 [39]，以高效的时间递归方式计算所需的后验分布。

 

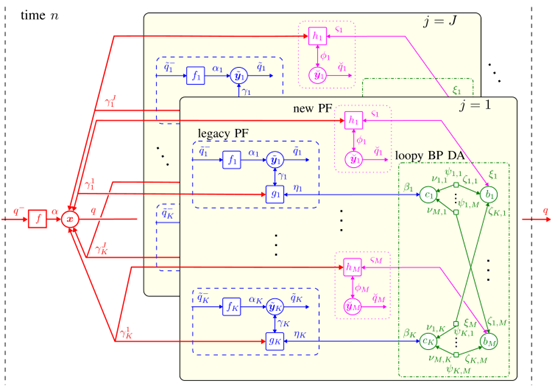
图2 因子图

A.检测和估计

 

B.信息传递算法

 

六、实验结果

A.分析设置

1）状态演化模型。

2）测量模型

3）通用仿真参数

 

B.综合测量结果

1）不同参数比较

        在 SLAM 1 和 SLAM 2 中，使用检测概率 Pd = 0.95 和平均误报数 μ(j) FA = 1。代理状态、旧 PF 状态和新 PF 状态分别由 100.000（SLAM 1）或 30.000（SLAM 2）粒子表示。在 SLAM 3 中，使用 Pd = 0.5 和 μ(j) FA =2 来分析 BP-SLAM 算法对极差无线电信号条件的鲁棒性，即，对于以现有 MPC 不存在的高概率为特征的场景检测到或检测到不存在的 MPC；此外，代理状态和 PF 状态均由 100.000 个粒子表示。

 

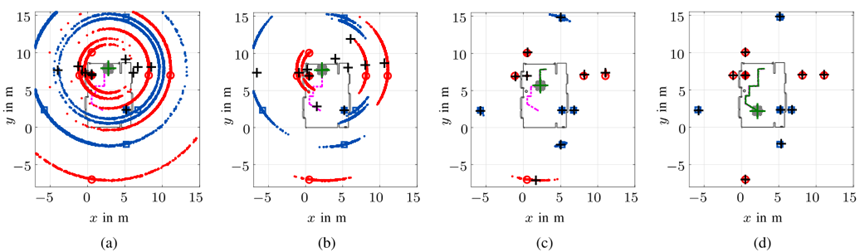
图3

        代表移动代理状态（灰色）和检测到的 PF 状态（红色代表 PA 1，蓝色代表 PA 2）的后验 pdf 的粒子显示在 (a) n = 3 0, ( b ) n = 9 0, ( c ) n = 3 0 0, a n d ( d ) n = 9 0 0。PA 1 和 PA 2 的位置分别用红色圆框和蓝色方框表示，对应的几何期望 V A 位置由红色圆圈和蓝色方块组成。绿线表示过去移动代理位置的 MMSE 估计，绿色交叉表示当前移动代理位置的 MMSE 估计。黑色十字表示检测到的 PF 位置的 MMSE 估计。

 

 

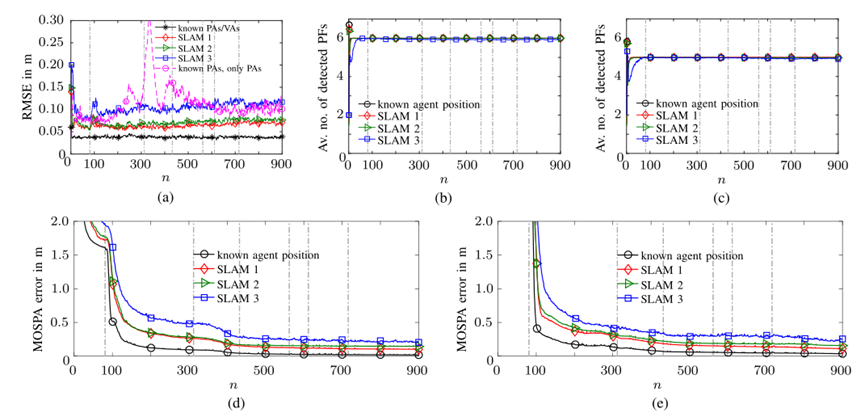
图4

        (a) 代理位置 RMSE，(b) 和 (c) 分别检测到与 PA 1 和 2 相关的 PF 的平均数量，(d) PA 1 和相关 VAs 的 MOSPA 误差，以及（e ) PA 2 和相关 V As 的 MOSPA 误差。在 (a) 中，标记为“known PAs/V As”的曲线显示了与基准算法的比较，该算法假定了解特征图，即 PA 和 VA 位置，以及标记为“known PAs, only PAs”的曲线显示了与仅使用两个 PA 位置（即没有 VA 位置）的基准算法的比较。在 (b)–(e) 中，标记为“已知代理位置”的曲线显示了代理位置已知的情况。

 

2）与 Rao-Blackwellized SLAM 的比较：将 BP-SLAM 算法的准确性和复杂性（运行时）与 RB-SLAM [2]、[13]、[20] 的算法进行比较，后者是一种重要的最新方法。我们注意到，RB-SLAM 可以通过将代理状态和所有特征状态堆叠到一个高维联合状态并使用粒子滤波器跟踪联合状态的想法来激发。由于维数灾难 [1]，直接实现这个想法通常是不可行的，我们的仅范围测量模型进一步加剧了这种情况。事实上，即使在仿真设置 SLAM 1 中使用的 100.000 个粒子也完全不足以表示联合状态向量。RB-SLAM 算法通过利用特征状态的条件独立性（以代理状态为条件）并将 Rao-Blackwellization 应用于联合状态 [1]，[20，Sec. 13]。

        因为本文的测量模型是高度非线性的，所以采用了 [13] 中提出的 RB-SLAM 实现，它使用粒子滤波器而不是 EKF 来估计特征状态。 （请注意，只实现了 [13] 中提出的 SLAM 算法，而不是包含通道估计器/跟踪器的完整两阶段方法。）由于测量特征关联未知，我们分别对每个粒子执行基于蒙特卡罗的 DA，因为它通常在经典 RB-SLAM [2]、[20] 中完成。经典的 RB-SLAM 算法对漏检和杂波测量非常敏感，特别是对于我们的 range-only 测量模型，这意味着很强的 DA 不确定性。因此，为了避免 RB-SLAM 发散的风险，我们在模拟中假设没有漏检或误报，即我们使用 Pd =1 和 μ(j) FA =0 生成数据。

 

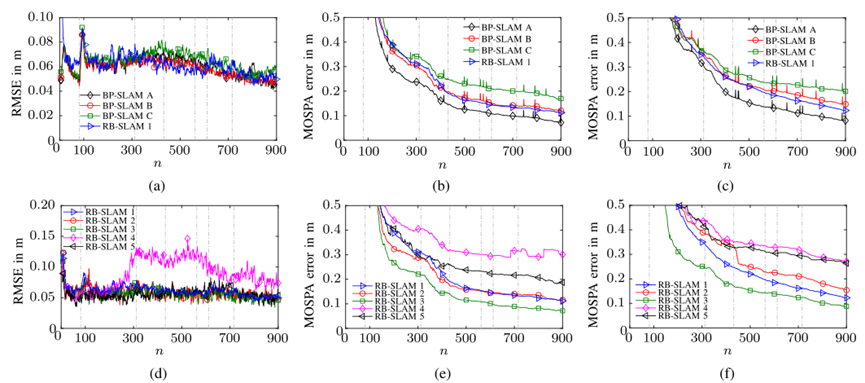
图5

 

        图 5 显示了估计代理位置的 RMSE 和两个 PAs 和相关 VAs 的 MOSPA 误差。对于 BP-SLAM，我们考虑了三种不同的参数设置，称为 BP-SLAM A-C，其中每个后验状态 pdf（对于代理状态、每个遗留 PF 状态和每个新 PF 状态）由 50.000（BP- SLAM A）、10.000（BP-SLAM B）或 5.000（BP-SLAM C）粒子。对于 RB-SLAM，考虑了五种不同的参数设置，称为 RB-SLAM 1-5，其中代理状态的后验 pdf 和每个特征状态的后验 pdf 分别由 50 和 10.000 表示（RB-SLAM 1)、100 和 5.000 (RB-SLAM 2)、100 和 10.000 (RB-SLAM 3)、500 和 1.000 (RB-SLAM 4)，或 1.000 和 1.000 (RB-SLAM 5) 粒子。在图 5（a）中，可以看出使用 BP-SLAM A-C 和 RB-SLAM 1 获得的代理位置 RMSE 通常非常相似。另一方面，图 5(b) 和 (c) 表明，正如所料，BP-SLAM 的 MOSPA 误差对于更多的粒子来说更小。RB-SLAM 1 的 MOSPA 误差仅略小于 BP-SLAM B（这是比较的良好基础，因为 RB-SLAM 1 也为每个特征状态使用 10.000 个粒子）。鉴于 BP-SLAM 假定代理状态和所有特征状态的先验独立性这一事实，这是值得注意的。 BP-SLAM A 甚至比 RB-SLAM 具有更小的 MOSPA 错误。图 5(d)–(f)比较不同RB-SLAM参数设置的RMSE和MOSPA误差结果；现在将讨论这些结果。

        BP-SLAM 比 RB-SLAM 1 复杂得多；特别是 BP-SLAM B 的运行时间——即使用与RB-SLAM 1 相同参数，只导致性能稍差——小了 10 多倍。这是因为 RB-SLAM 计算了每个代理状态粒子到每个特征状态粒子的距离。因此，RB-SLAM 的复杂性与代理粒子数量和特征粒子总数的乘积呈线性关系；相比之下，BP-SLAM 的复杂性与所有粒子的数量呈线性关系。可以得出结论，相对于 BP-SLAM B，RB-SLAM 的准确度稍微好一些，但代价是复杂度高得多。我们注意到，使用粒子来表示特征状态的 RB-SLAM 算法的复杂性可以通过 [27] 中提出的自适应重采样算法来降低。

从这些运行时结果和图。从图 5(d)–(f) 可以进一步得出以下结论：(i) 增加 RB-SLAM 中代理粒子的数量只会略微增加代理状态和 VA 位置估计的准确性，但会显着增加计算复杂度。(ii) 减少 RB-SLAM 中 VA 粒子的数量会显着降低代理状态和 VA 位置估计的准确性，甚至可能导致代理状态发散，因为 VA 粒子会聚到错误的位置。（在这里，如果误差超过 30 厘米并继续增加，我们认为模拟运行是发散的。请注意，图 5(d)-(f) 中绘制的代理位置 RMSE 和 PA/VA MOSPA 误差是计算出来的仅对各自的参数设置使用收敛的模拟运行. 对于参数设置 RB-SLAM 1–3，所有模拟运行都收敛了。对于参数设置 RB-SLAM 4 和 RB-SLAM 5，分别只有 73% 和 87% 的模拟运行收敛。）

C.实际测量结果

        为了使用实际测量来评估所提出的 BP-SLAM 算法的性能，选择 Pd = 0.6 和 μ(j) FA = 2。这解释了由于室内环境中存在的扩散多径，初步信道估计表现出较低的检测概率和较高的误报概率。

        这些测量值取自先前在 [33]、[60] 中使用的研讨室场景。它们对应于五个紧密间隔的平行轨迹，每个轨迹由 900 个代理位置组成，沿每个轨迹的间距为 0.01m，轨迹之间的间距为 0.01m，总共有 4500 个代理位置。图 1 中的洋红色线代表五个轨迹之一。[60] 中提供了有关测量的更多详细信息；特别是，[60，图 1] 中显示了五个轨迹的特写。在每个代理位置，代理发送超宽带信号，由两个静态 PA 接收。该信号是使用频率范围为 3–10 GHz 的 M 序列相关信道发声器和在方位角平面上具有近似均匀辐射图的天线以及在地板和天花板方向上具有零点的天线测量的。在测量频带内，实际信号频带由具有升余弦脉冲响应、滚降系数为 0.5、两侧 3 dB 带宽为 2 GHz、中心频率为 7 GHz 的滤波器选择。进行了 30 次模拟运行。每个状态的 pdf 由 30.000 个粒子表示。每个单独的轨迹都是独立处理的，即轨迹的估计 PF 位置不用作另一个轨迹的先验知识。

 

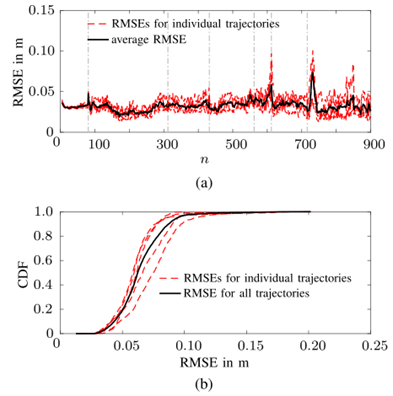
图6

        图 6(a) 显示了针对五个轨迹单独获得的 BP-SLAM 代理位置 RMSE 随时间 n 的变化，以及在五个轨迹上平均的整体 RMSE。图 6(b) 显示了单个 RMSE 的经验累积分布函数 (CDF) 和五个 RMSE 的经验累积分布函数。可以看出，在 RMSE 等于 0.12m 甚至更小时，各个 CDF 已经非常接近 1。所有单个 RMSE 的最大值在所有情况下都低于 0.2m，在所有情况下的 90% 都低于 0.083m。

 

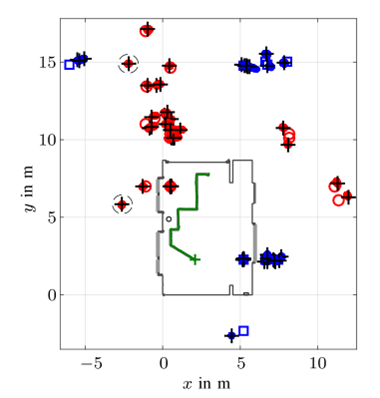
图7

        对于示例性模拟运行，图 7 描绘了代表检测到的 PF 状态的后验 pdf 的粒子，以及对五个轨迹在当前时刻检测到的 PF 位置的 MMSE 估计。此外，图 7 描述了过去和当前移动代理位置的 MMSE 估计。几乎所有估计的 PF 位置都可以与几何上预期的 VA 位置相关联。这表明 BP-SLAM 算法能够利用无线电信号中包含的位置相关信息来进行准确和稳健的定位。

七、结论和未来展望

        提出了一种基于无线电信号的具有概率 DA 的 SLAM 算法。底层系统模型描述具有未知且可能随时间变化的位置的 VAs 方面的镜面 MPC。为了解决 DA 问题，即 MPC 与 V As 的未知关联，我们对整个 SLAM 问题进行了建模，包括贝叶斯框架中的概率 DA。然后，我们用因子图表示联合后验分布的因式分解，并应用 BP 对联合后验分布进行近似边缘化。这种方法允许为概率 DA 合并一个有效的 BP 算法，该算法最初是为 MTT [40]、[42] 提出的。我们的因子图通过新的潜在特征的状态扩展了 [33] 的因子图。

        使用合成数据的仿真结果表明，即使在强杂波和低检测概率的情况下，所提出的 BP-SLAM 算法也能以高精度和鲁棒性估计时变代理位置和特征图。此外，在室内环境中使用真实超宽带无线电信号进行的实验分析表明，BP-SLAM 算法在现实场景中的表现同样出色；观察到 100% 的代理位置误差低于 0.2m，90% 的所有测量值低于 0.083m。

        未来研究的有前途的方向是利用更多的 MPC 参数，如 AoAs 和 AoDs，以包括其他类型的特征，如散点，并重新定义要扩展对象的特征。最后，研究非同步传感器网络中的操作和分布式（去中心化）操作模式会很有趣。

 参考文献

[1] S. Thrun, W. Burgard, and D. Fox, Probabilistic Robotics. Cambridge,MA, USA: MIT Press, 2006.

一本书，以概率分布的观点思考机器人技术问题，是SLAM初期的理论

 

[2] H. Durrant-Whyte and T. Bailey, “Simultaneous localization and mapping: Part I,” IEEE Robot. Autom. Mag., vol. 13, no. 2, pp. 99–110,Jun. 2006.

FastSLAM ，SLAM最早被提出来的文章，这是Part 1 ，还有一个Part 2。

 

[3] G. Bresson, Z. Alsayed, L. Y u, and S. Glaser, “Simultaneous localization and mapping: A survey of current trends in autonomous driving,” IEEE Trans. Intell. Veh., vol. 2, no. 3, pp. 194–220, Sep. 2017.

概述了SLAM的不同分支，然后详细介绍了在自动驾驶领域的经典方法和未来趋势。

 

[4] R. Di Taranto, S. Muppirisetty, R. Raulefs, D. Slock, T. Svensson, and H. Wymeersch, “Location-aware communications for 5G networks: How location information can improve scalability, latency, and robustness of 5G,” IEEE Signal Process. Mag., vol. 31, no. 6, pp. 102–112, Nov. 2014.

5G中位置感知技术的展望，预测趋势和面临的问题

 

[5] K. Witrisal et al., “High-accuracy localization for assisted living: 5G systems will turn multipath channels from foe to friend,” IEEE Signal Process. Mag., vol. 33, no. 2, pp. 59–70, Mar. 2016.

5G系统多径信息MPC用于高精度室内定位

 

[6] S. Bartoletti, A. Conti, A. Giorgetti, and M. Z. Win, “Sensor radar networks for indoor tracking,” IEEE Wireless Commun. Lett., v o l . 3 ,no. 2, pp. 157–160, Apr. 2014.

室内环境用雷达追踪目标的算法

 

[7] D . Dardari, P. Closas, and P.M. Djuri´c, “Indoor tracking: Theory,methods, and technologies,” IEEE Trans. Veh. Technol., vol. 64, no. 4,pp. 1263–1278, Apr. 2015.

室内，无线定位的多种方法，包括SLAM

 

[8] F. Guidi, A. Guerra, and D. Dardari, “Personal mobile radars withmillimeter-wave massive arrays for indoor mapping,” IEEE Trans.Mobile Comput., vol. 15, no. 6, pp. 1471–1484, Jun. 2016.

毫米波，使用MPC，大规模阵列天线雷达，室内测绘建图

 

[9] E. Leitinger, F. Meyer, P. Meissner, K. Witrisal, and F. Hlawatsch,“Belief propagation based joint probabilistic data association formultipath-assisted indoor navigation and tracking,” in Proc. Int. Conf.Localization GNSS (ICL-GNSS), Barcelona, Spain, Jun. 2016, pp. 1–6.

BP算法，利用MPC，室内定位跟踪

 

[10] H. Wymeersch, S. Marano, W. M. Gifford, and M. Z. Win, “A machine learning approach to ranging error mitigation for UWB localization,”IEEE Trans. Commun., vol. 60, no. 6, pp. 1719–1728, Jun. 2012.

在物理层上，使用SVG和高斯过程改进UWB定位

 

[11] Y . Shen, S. Mazuelas, and M. Z. Win, “Network navigation: Theory and interpretation,” IEEE J. Sel. Areas Commun., vol. 30, no. 9,pp. 1823–1834, Oct. 2012.

网格导航，提升精度，融合时空信息

 

[12] M. Z. Win, Y . Shen, and W. Dai, “A theoretical foundation of network localization and navigation,” Proc. IEEE, vol. 106, no. 7,pp. 1136–1165, Jul. 2018.

与[11]相同，时空信息合作的网格导航

 

[13] C. Gentner, T. Jost, W. Wang, S. Zhang, A. Dammann, and U.-C. Fiebig, “Multipath assisted positioning with simultaneous localization and mapping,” IEEE Trans. Wireless Commun., vol. 15, no. 9,pp. 6104–6117, Sep. 2016.

FastSLAM，利用多径MPC对移动代理进行位置估计的算法。应用基于递归贝叶斯过滤的新算法，称为Channel-SLAM。考虑多次反射，散射等MPC路径组合

 

[14] E. Leitinger, P. Meissner, C. Rüdisser, G. Dumphar, and K. Witrisal,“Evaluation of position-related information in multipath components for indoor positioning,” IEEE J. Sel. Areas Commun., vol. 33, no. 11,pp. 2313–2328, Nov. 2015.

利用MPC，提出一个同一框架来研究固定锚点的信号传输、代理之间的协作传输或类似雷达的单站传输的位置相关信息。

 

[15] A. Guerra, F. Guidi, J. Dall’Ara, and D. Dardari, “Occupancy grid mapping for personal radar applications,” in Proc. IEEE SSP, Freiburg, Germany, Jun. 2018, pp. 766–770.

个人雷达，网格占用的建图方法

 

[16] H. Zhang and S. Y . Tan, “TOA based indoor localization and tracking via single-cluster PHD filtering,” in Proc. IEEE Global Commun. Conf.,Singapore, Dec. 2017, pp. 1–6.

利用多径MPC，测量TOA，粒子-高斯混合的PHD滤波器

 

[17] J. Borish, “Extension of the image model to arbitrary polyhedra,” J. Acoust. Soc. Amer., vol. 75, no. 6, pp. 1827–1836, Mar. 1984.

任意多面体反射位置的算法，VA/PA

 

[18] M. W. M. G. Dissanayake, P . Newman, S. Clark, H. F. Durrant-Whyte,and M. Csorba, “A solution to the simultaneous localization and map building (SLAM) problem,” IEEE Trans. Robot. Autom., vol. 17, no. 3,pp. 229–241, Jun. 2001.

EKF，SLAM早期文章

 

[19] J. Mullane, B.-N. V o, M. D. Adams, and B.-T. V o, “A random-finite-set approach to Bayesian SLAM,” IEEE Trans. Robot., vol. 27, no. 2,pp. 268–282, Apr. 2011.

贝叶斯框架，PHD滤波器的一阶解，基于集合（set）的SLAM

 

[20] M. Montemerlo, S. Thrun, D. Koller, and B. Wegbreit, “FastSLAM: A factored solution to the simultaneous localization and mapping problem,”in Proc. AAAI, Edmonton, AB, Canada, Jul. 2002, pp. 593–598.

FastSLAM的源文章

 

[21] M. Lundgren, L. Svensson, and L. Hammarstrand, “Variational Bayesian expectation maximization for radar map estimation,” IEEE Trans. Signal Process., vol. 64, no. 6, pp. 1391–1404, Mar. 2016.

贝叶斯变分，雷达的自我定位，

 

[22] M. Fatemi, L. Svensson, L. Hammarstrand, and M. Lundgren, “Variational Bayesian EM for SLAM,” in Proc. IEEE CAMSAP, Cancun, Mexico, Dec. 2015, pp. 501–504.

贝叶斯变分，雷达，数据融合

 

[23] H. Deusch, S. Reuter, and K. Dietmayer, “The labeled multi-Bernoulli SLAM filter,” IEEE Signal Process. Lett., vol. 22, no. 10,pp. 1561–1565, Oct. 2015.

基于集合set的SLAM，多伯努利滤波器的SLAM

 

[24] M. Fatemi, K. Granström, L. Svensson, F. J. R. Ruiz, and L. Hammarstrand, “Poisson multi-Bernoulli mapping using Gibbs sampling,” IEEE Trans. Signal Process., vol. 65, no. 11,pp. 2814–2827, Jun. 2017.

基于集合set的SLAM，吉布斯采样，

 

[25] E. Leitinger, P. Meissner, M. Lafer, and K. Witrisal, “Simultaneous localization and mapping using multipath channel information,” in Proc. IEEE ICCW, London, U.K., Jun. 2015, pp. 754–760.

MPC的SLAM，使用VA特征。

 

[26] M. Zhu, J. Vieira, Y . Kuang, K. Astrom, A. F. Molisch, and F. Tufvesson, “Tracking and positioning using phase information from estimated multi-path components,” in Proc. IEEE ICCW, London, U.K., Jun. 2015, pp. 712–717.

EKF获得MPC相位，TDOA定位移动设备

 

[27] C. Gentner, R. Pöhlmann, M. Ulmschneider, T. Jost, and S. Zhang,“Positioning using terrestrial multipath signals and inertial sensors,” Mobile Inf. Syst., vol. 2017, Oct. 2017, Art. no. 9170746.

粒子滤波，channel-SLAM，MPC，IMU

 

[28] B. H. Fleury, M. Tschudin, R. Heddergott, D. Dahlhaus, and K. I. Pedersen, “Channel parameter estimation in mobile radio environments using the SAGE algorithm,” IEEE J. Sel. Areas Commun.,vol. 17, no. 3, pp. 434–450, Mar. 1999.

信道建模，从MPC提取

 

[29] A. Richter, “Estimation of Radio Channel Parameters,” Ph.D. dissertation, Inst. Commun. Meas., Ilmenau Univ. Technol.,Ilmenau, Germany, 2005.

估计信道参数

 

[30] D. Shutin and B. H. Fleury, “Sparse variational Bayesian SAGE algorithm with application to the estimation of multipath wireless channels,” IEEE Trans. Signal Process., vol. 59, no. 8, pp. 3609–3623, Aug. 2011.

SAGE估计信道MPC参数

 

[31] J. Salmi, A. Richter, and V . Koivunen, “Detection and tracking of MIMO propagation path parameters using state-space approach,” IEEE Trans. Signal Process., vol. 57, no. 4, pp. 1538–1550, Apr. 2009.

密集多径分量DMC，测量多径信道参数

 

[32] M. A. Badiu, T. L. Hansen, and B. H. Fleury, “Variational Bayesian inference of line spectra,” IEEE Trans. Signal Process., vol. 65, no. 9, pp. 2247–2261, May 2017.

变分推理，线谱估计

 

[33] E. Leitinger, F. Meyer, F. Tufvesson, and K. Witrisal, “Factor graph based simultaneous localization and mapping using multipath channel information,” in Proc. IEEE ICC, Paris, France, May 2017, pp. 652–658.

BP算法，因子图，使用MPC

 

[34] Y . Bar-Shalom, P. K. Willett, and X. Tian, Tracking and Data Fusion: A Handbook of Algorithms. Storrs, CT, USA: Y aakov Bar-Shalom, 2011.

多目标跟踪的一本书，估计理论

 

[35] D. Musicki and R. Evans, “Joint integrated probabilistic data association: JIPDA,” IEEE Trans. Aerosp. Electron. Syst., vol. 40, no. 3,pp. 1093–1099, Jul. 2004.

杂波干扰下多目标跟踪的联合集成概率数据关联JIPDA滤波器，可从杂波干扰中找到先验信息。

 

[36] P. Horridge and S. Maskell, “Searching for, initiating and tracking multiple targets using existence probabilities,” in Proc. 12th Int. Conf. Inf. Fusion, Seattle, W A, USA, Jul. 2009, pp. 611–617.

JIPDA滤波器，用于搜索和跟踪多个目标，使用存在概率来执行跟踪管理。使用存在概率来启动新的轨道。

 

[37] P. R. Horridge and S. Maskell, “Using a probabilistic hypothesis density filter to confirm tracks in a multi-target environment,” in Proc. INFORMATIK, Berlin, Germany, Jul. 2011, pp. 1–12.

PHD滤波器，多目标检测

 

[38] H.-A. Loeliger, “An introduction to factor graphs,” IEEE Signal Process. Mag., vol. 21, no. 1, pp. 28–41, Jan. 2004.

因子图源文章，梯度方法，卡尔曼滤波和粒子方法都可以用作因子图的组件，BP传播

 

[39] F. R. Kschischang, B. J. Frey, and H.-A. Loeliger, “Factor graphs and the sum-product algorithm,” IEEE Trans. Inf. Theory, vol. 47, no. 2, pp. 498–519, Feb. 2001.

消息传递算法（总和乘积算法），因子图，涉及BP传播

 

[40] J. Williams and R. Lau, “Approximate evaluation of marginal association probabilities with belief propagation,” IEEE Trans. Aerosp. Electron. Syst., vol. 50, no. 4, pp. 2942–2959, Oct. 2014.

BP传播，多目标检测MTT。

 

[41] F. Meyer et al., “Message passing algorithms for scalable multitarget tracking,” Proc. IEEE, vol. 106, no. 2, pp. 221–259, Feb. 2018.

BP算法，MTT，非线性非高斯，单/多传感器场景，随机有限集RFS

 

[42] F. Meyer, P. Braca, P. Willett, and F. Hlawatsch, “A scalable algorithm for tracking an unknown number of targets using multiple sensors,” IEEE Trans. Signal Process., vol. 65, no. 13, pp. 3478–3493, Jul. 2017.

BP传播，MTT

 

[43] G. Soldi, F. Meyer, P. Braca, and F. Hlawatsch, “Self-tuning algorithms for multisensor-multitarget tracking using belief propagation,” IEEE Trans. Signal Process., vol. 67, no. 15, pp. 3922–3937, Aug. 2019.

BP传播，MTT

 

[44] J. L. Williams, “Marginal multi-Bernoulli filters: RFS derivation of MHT, JIPDA, and association-based MeMBer,” IEEE Trans. Aerosp. Electron. Syst., vol. 51, no. 3, pp. 1664–1687, Jul. 2015.

随机有限集RFS，BP方法，MTT，有开源

 

[45] T. Kropfreiter, F. Meyer, and F. Hlawatsch, “Sequential Monte Carlo implementation of the track-oriented marginal multi-Bernoulli/Poisson filter,” in Proc. FUSION, Heidelberg, Germany, Jul. 2016, pp. 972–979.

TOMB/P-SMC滤波器，RFS，BP，MTT

 

[46] A. D. Marrs, “Asynchronous multi-sensor tracking in clutter with uncertain sensor locations using Bayesian sequential Monte Carlo methods,” in Proc. IEEE Aerosp. Conf., Big Sky, MT, USA, vol. 5, Mar. 2001,pp. 2171–2178.

贝叶斯方法，多传感器且位置不确定，应对高不确定性场景

 

[47] J. Blanco, J. Gonzalez, and J. Fernandez-Madrigal, “A pure probabilistic approach to range-only SLAM,” in Proc. IEEE ICRA, Pasadena, CA, USA, May 2008, pp. 1436–1441.

允许引入新信标，处理仅距离信息的SLAM

 

[48] C. Gentner and T. Jost, “Indoor positioning using time difference of arrival between multipath components,” in Proc. IPIN, Montbeliard-Belfort, France, Oct. 2013, pp. 1–10.

MPC的TOA定位，只用时差。

 

[49] B. Etzlinger, F. Meyer, F. Hlawatsch, A. Springer, and H. Wymeersch, “Cooperative simultaneous localization and synchronization in mobile agent networks,” IEEE Trans. Signal Process., vol. 65, no. 14, pp. 3587–3602, Jul. 2017.

BP置信传播算法，代理与基站的同步

 

[50] E. Leitinger, S. Grebien, X. Li, F. Tufvesson, and K. Witrisal, “On the use of MPC amplitude information in radio signal based SLAM,” in Proc. IEEE SSP, Freiburg, Germany, Jun. 2018, pp. 633–637.

利用MPC幅度，以时变的方式调整检测无线电信号中特征的概率

 

[51] P. Meissner, “Multipath-assisted indoor positioning,” Ph.D. dissertation, Signal Process. Speech Commun. Lab., Graz Univ. Technol.,Graz, Austria, 2014.

有高阶VA的描述

 

[52] T. Jost, W. Wang, U.-C. Fiebig, and F. Pérez-Fontán, “Detection and tracking of mobile propagation channel paths,” IEEE Trans. Antennas Propag., vol. 60, no. 10, pp. 4875–4883, Oct. 2012.

检测MPC信道参数

 

[53] J. Vermaak, S. J. Godsill, and P. Perez, “Monte Carlo filtering for multitarget tracking and data association,” IEEE Trans. Aerosp. Electron.Syst., vol. 41, no. 1, pp. 309–332, Jan. 2005.

多目标的数据联合，

 

[54] S. Kay, Fundamentals of Statistical Signal Processing: Estimation Theory, vol. 1. Upper Saddle River, NJ, USA: Prentice-Hall, 1993.

统计信号过程，MMSE

 

[55] F. Meyer, O. Hlinka, H. Wymeersch, E. Riegler, and F. Hlawatsch, “Distributed localization and tracking of mobile networks including noncooperative objects,” IEEE Trans. Signal Inf. Process. Net., v o l . 2 ,no. 1, pp. 57–71, Mar. 2016.

基于粒子的BP，分布式多代理定位

 

[56] Y . Bar-Shalom, T. Kirubarajan, and X.-R. Li, Estimation With Applications to Tracking and Navigation. New Y ork, NY , USA: Wiley, 2002.

一本书

 

[57] D. Schuhmacher, B.-T. V o, and B.-N. V o, “A consistent metric for performance evaluation of multi-object filters,” IEEE Trans. Signal Process., vol. 56, no. 8, pp. 3447–3457, Aug. 2008.

多对象指标评估

 

[58] A. S. Rahmathullah, Á. F. García-Fernández, and L. Svensson, “Generalized optimal sub-pattern assignment metric,” in Proc. FUSION, X i ’ a n , China, Jul. 2017, pp. 1–8.

最优子模式赋值 （OSPA） 指标的升级GOSPA

 

[59] A. W. Moore, “Very fast EM-based mixture model clustering using multiresolution kd-trees,” in Proc. NIPS, Denver, CO, USA, Dec. 1998, pp. 543–549.

几何数据结构kd-trees，降低复杂度

 

[60] P. Meissner, E. Leitinger, and K. Witrisal, “UWB for robust indoor tracking: Weighting of multipath components for efficient estimation,” IEEE Wireless Commun. Lett., vol. 3, no. 5, pp. 501–504, Oct. 2014.

实际的数据集，2D平面