基于矩阵分解的推荐算法,简单入门
本文将要讨论基于矩阵分解的推荐算法,这一类型的算法通常会有很高的预测精度,也活跃于各大推荐系统竞赛上面,前段时间的百度电影推荐最终结果的前10名貌似都是把矩阵分解作为一个单模型,最后各种ensemble,不知道正在进行的阿里推荐比赛(http://102.alibaba.com/competition/addDiscovery/index.htm),会不会惊喜出现。。。。好了,闲话不扯了,本文打算写一篇该类型推荐算法的入门篇
目录
一,基于矩阵分解的推荐算法相关理论介绍
二,C++代码实现
三,总结跟展望一下
四,后续计划
一,基于矩阵分解的推荐算法相关理论介绍
我们知道,要做推荐系统,最基本的一个数据就是,用户-物品的评分矩阵,如下图1所示

图1
矩阵中,描述了5个用户(U1,U2,U3,U4 ,U5)对4个物品(D1,D2,D3,D4)的评分(1-5分),- 表示没有评分,现在目的是把没有评分的 给预测出来,然后按预测的分数高低,给用户进行推荐。
如何预测缺失的评分呢?对于缺失的评分,可以转化为基于机器学习的回归问题,也就是连续值的预测,对于矩阵分解有如下式子,R是类似图1的评分矩阵,假设N*M维(N表示行数,M表示列数),可以分解为P跟Q矩阵,其中P矩阵维度N*K,P矩阵维度K*M。

式子1
对于P,Q矩阵的解释,直观上,P矩阵是N个用户对K个主题的关系,Q矩阵是K个主题跟M个物品的关系,至于K个主题具体是什么,在算法里面K是一个参数,需要调节的,通常10~100之间。

式子2
对于式子2的左边项,表示的是R^ 第i行,第j列的元素值,对于如何衡量,我们分解的好坏呢,式子3,给出了衡量标准,也就是损失函数,平方项损失,最后的目标,就是每一个元素(非缺失值)的e(i,j)的总和 最小

式子3
OK,目前现在评分矩阵有了,损失函数也有了,该优化算法登场了,下面式子4是,基于梯度下降的优化算法,p,q里面的每个元素的更新方式


式子4
然而,机器学习算法都喜欢加一个正则项,这里面对式子3稍作修改,得到如下式子5,beita 是正则参数

式子5
相应的p,q矩阵各个元素的更新也换成了如下方式

式子6
至此,P,Q矩阵元素求出来了之后,计算某个用户i对某个物品j的评分计算就是p(i,1)*q(1,j)+p(i,2)*q(2,j)+....+p(i,k)*q(k,j)。
二,C++代码实现
第一部分已经给出了,基于矩阵分解的推荐算法的整个流程,下面是该算法编程实现(C/C++),代码加一些注释有助于理解
1 /**
2
3 评分矩阵R如下
4
5 D1 D2 D3 D4
6
7 U1 5 3 - 1
8
9 U2 4 - - 1
10
11 U3 1 1 - 5
12
13 U4 1 - - 4
14
15 U5 - 1 5 4
16
17 ***/
18
19 #include<iostream>
20
21 #include<cstdio>
22
23 #include<cstdlib>
24
25 #include<cmath>
26
27 using namespace std;
28
29
30
31 void matrix_factorization(double *R,double *P,double *Q,int N,int M,int K,int steps=5000,float alpha=0.0002,float beta=0.02)
32
33 {
34
35 for(int step =0;step<steps;++step)
36
37 {
38
39 for(int i=0;i<N;++i)
40
41 {
42
43 for(int j=0;j<M;++j)
44
45 {
46
47 if(R[i*M+j]>0)
48
49 {
50
51 //这里面的error 就是公式6里面的e(i,j)
52
53 double error = R[i*M+j];
54
55 for(int k=0;k<K;++k)
56
57 error -= P[i*K+k]*Q[k*M+j];
58
59
60
61 //更新公式6
62
63 for(int k=0;k<K;++k)
64
65 {
66
67 P[i*K+k] += alpha * (2 * error * Q[k*M+j] - beta * P[i*K+k]);
68
69 Q[k*M+j] += alpha * (2 * error * P[i*K+k] - beta * Q[k*M+j]);
70
71 }
72
73 }
74
75 }
76
77 }
78
79 double loss=0;
80
81 //计算每一次迭代后的,loss大小,也就是原来R矩阵里面每一个非缺失值跟预测值的平方损失
82
83 for(int i=0;i<N;++i)
84
85 {
86
87 for(int j=0;j<M;++j)
88
89 {
90
91 if(R[i*M+j]>0)
92
93 {
94
95 double error = 0;
96
97 for(int k=0;k<K;++k)
98
99 error += P[i*K+k]*Q[k*M+j];
100
101 loss += pow(R[i*M+j]-error,2);
102
103 for(int k=0;k<K;++k)
104
105 loss += (beta/2) * (pow(P[i*K+k],2) + pow(Q[k*M+j],2));
106
107 }
108
109 }
110
111 }
112
113 if(loss<0.001)
114
115 break;
116
117 if (step%1000==0)
118
119 cout<<"loss:"<<loss<<endl;
120
121 }
122
123 }
124
125
126
127 int main(int argc,char ** argv)
128
129 {
130
131 int N=5; //用户数
132
133 int M=4; //物品数
134
135 int K=2; //主题个数
136
137 double *R=new double[N*M];
138
139 double *P=new double[N*K];
140
141 double *Q=new double[M*K];
142
143 R[0]=5,R[1]=3,R[2]=0,R[3]=1,R[4]=4,R[5]=0,R[6]=0,R[7]=1,R[8]=1,R[9]=1;
144
145 R[10]=0,R[11]=5,R[12]=1,R[13]=0,R[14]=0,R[15]=4,R[16]=0,R[17]=1,R[18]=5,R[19]=4;
146
147
148
149 cout<< "R矩阵" << endl;
150
151 for(int i=0;i<N;++i)
152
153 {
154
155 for(int j=0;j<M;++j)
156
157 cout<< R[i*M+j]<<',';
158
159 cout<<endl;
160
161 }
162
163
164
165 //初始化P,Q矩阵,这里简化了,通常也可以对服从正态分布的数据进行随机数生成
166
167 srand(1);
168
169 for(int i=0;i<N;++i)
170
171 for(int j=0;j<K;++j)
172
173 P[i*K+j]=rand()%9;
174
175
176
177 for(int i=0;i<K;++i)
178
179 for(int j=0;j<M;++j)
180
181 Q[i*M+j]=rand()%9;
182
183 cout <<"矩阵分解 开始" << endl;
184
185 matrix_factorization(R,P,Q,N,M,K);
186
187 cout <<"矩阵分解 结束" << endl;
188
189
190
191 cout<< "重构出来的R矩阵" << endl;
192
193 for(int i=0;i<N;++i)
194
195 {
196
197 for(int j=0;j<M;++j)
198
199 {
200
201 double temp=0;
202
203 for (int k=0;k<K;++k)
204
205 temp+=P[i*K+k]*Q[k*M+j];
206
207 cout<<temp<<',';
208
209 }
210
211 cout<<endl;
212
213 }
214
215 free(P),free(Q),free(R);
216
217 return 0;
218
219 }
执行的结果如下图所示,
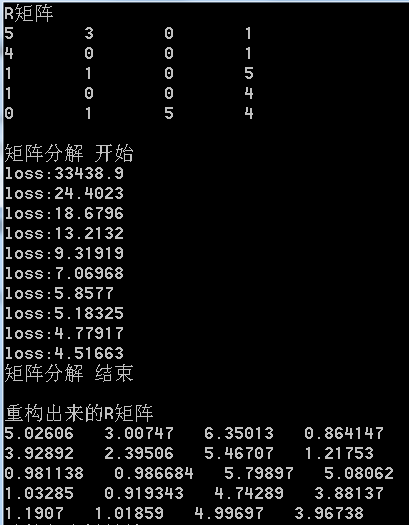
三,展望
前两个部分,已经简单的介绍了最基本的基于矩阵分解的推荐算法,基于该算法的一些变种,类似svd++,pmf等,都是针对某一些特定的数据场景进行的一些改进,那有没有统一的框架来整合这些场景呢??前两年在KDDcup大赛,大出风头的Factorization Machine(FM),其中FM的核心理论在于用Factorization来刻画feature跟feature之间的关系,如下面公式
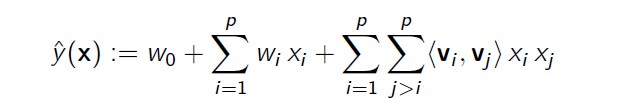
<Vi,Vj>正是刻画了xi,xj的关系,上面式子可以理解为FM=SVM+Factorization Methods,后续准备开一篇博文,来阐释FM模型,跟其作者开源的LibFM工具箱,最后贴一张八卦的图,图中讲的是bickson(graphlab/graphchi的里面推荐工具包的作者),在一次会议上,对steffen(libfm的作者)问的一个问题

四,后续计划
1),介绍FM模型
2),LibFM源码剖析
参考资料
1),bickson.blogspot.com/2012/08/steffen-rendle-libfm.html
2),S. Rendle.Factorization machines.In Proceedings of the 10th IEEE International Conference on Data Mining. IEEE Computer Society, 2010.

