「组合数学」一:什么是组合数学
好怪的标题
前言
组合数学所关心的问题就是把某个集合中的对象排列成某种模式,使其满足一些指定的规则。
排列的存在性和排列的列举或分类是两种反复出现的通用问题
排列数量较小时我们可以枚举,当数量较大时我们就要考虑在不列出它们的情况下确定这些排列的技术问题
还有另外两种常常出现的组合问题:研究已知排列和构造最优排列
因此,关于组合数学的一般描述也许就是:\(组合数学是研究离散构造的存在、计数、分析和优化等问题的一门学科\)。
组合数学验证发现的主要工具之一是\(数学归纳法\)。
通常用数学归纳法证明一个较强的结果比证明一个较弱的结果更容易
组合数学的一个典型解决方法可能包含下面几个步骤:
\(1.\)建立数学模型
\(2.\)研究模型
\(3.\)计算若干小样例(打表)
\(4.\)推理计算出答案(找规律)
例一:棋盘的完美覆盖问题
先考虑一张普通\(8*8\)棋盘,有一些\(1*2\)的多米诺骨牌,是否能够把\(32\)张多米诺骨牌不重不漏地摆放在棋盘上,形成棋盘的多米诺完美覆盖。
我们可以很简单地求得一个方案,也可以不是很简单地算出方案数\(12988816=2^4*17^2*53^2\)
更一般地,有\(m*n\)的棋盘,此时它的完美覆盖不一定存在。比如对于\(3*3\)的棋盘来说就不存在完美覆盖。不难看出,当\(n,m\)中至少有一个数是偶数时,或者是棋盘格子的总数是偶数时才存在完美覆盖
\(Fischer\)得出了计算\(m*n\)的棋盘的不同完美覆盖的一般公式,这个公式中含有三角函数
再考虑\(8*8\),去掉一条对角线上两个对角的方格,剩下的\(62\)个方格不存在完美覆盖,可以用黑白染色来证明,去掉的两个格子一定同色
更一般地,取一个\(m*n\)棋盘黑白染色,随机去掉一些方格,存在完美匹配的必要条件是剩下的黑格和白格数量相等
充要条件以后再谈
再拓展,对于\(m*n\)棋盘,用\(1*b\)的牌完美覆盖问题
为了有完美覆盖,\(b\)必须是\(mn\)的一个因子。
显然存在完美覆盖的一个充分条件是,\(b\)必须是\(m\)或\(n\)的一个因子
当\(b\)是素数时,上述条件是充要条件
当\(b\)不是素数时,假设完美覆盖存在,我们要证明\(m\)或\(n\)被\(b\)整除时余数是\(0\),设
不妨设\(b\)是\(m\)的因子,于是我们要证明\(r=0\)
现在把黑白染色推广到\(b\)种颜色的情况,按下列方式染色
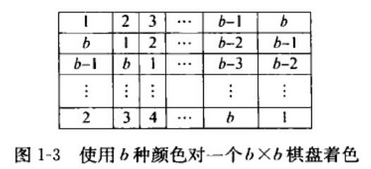
完美覆盖的每一张\(b\)格牌覆盖\(b\)个方格,且每一个方格覆盖一种颜色。于是,棋盘上每一种颜色的方格数一定相同
我们将棋盘分为三部分,上方\(pb*n\)部分,左下方\(r*qb\)部分,右下方\(r*s\)部分,易证前两部分颜色数一定相同,只考虑右下方\(r*s\)部分,若要每种颜色格数相同,只有\(r\neq 0,s=b\)或\(r=0\)
由此得出:
\(m*n棋盘有1*b牌的完美覆盖当且仅当b是m或n的一个因子\)
根据上述染色方法我们还可以改述上述结论:
如果完美覆盖中所有\(1*b\)牌都是水平或竖直放置,则称这样的完美覆盖是平凡的。存在完美覆盖当且仅当存在平凡覆盖
下面考虑一个很有特色的多米诺骨牌问题:
考虑\(4*4\)的棋盘,用\(8\)张多米诺骨牌可以完美覆盖,证明:
总可以把这个棋盘横着或竖着切成非空两块而不切断任意一张多米诺骨牌
称这样的切割直线为这个完美覆盖的断层线。因此,一条水平断层线表示这个\(4*4\)的棋盘的完美覆盖是由两个完美覆盖组成的:对于某个\(k=1,2,3,…,\)一个是\(k*4\)的完美覆盖,另一个是\((4*k)*4\)的完美覆盖。
假设\(4*4\)的棋盘存在一个不存在断层线的完美覆盖,设\(x_1,x_2,x_3\)分别是被三条水平切割线切到的多米诺骨牌数
因为不存在断层线,所以\(x_1,x_2,x_3>0\),一个水平方向多米诺骨牌在一行覆盖两个方格,一个竖直方向多米诺骨牌在两行上分别覆盖一个方格,由此可以得出\(x_1,x_2,x_3\)都是偶数,即
而且在这个完美覆盖中至少有\(6\)个竖直方向上的多米诺骨牌。
用类似的方法我们可以得出至少有\(6\)个水平方向上的多米诺骨牌。
而\(6+6=12>8\),所以\(4*4\)棋盘的完美覆盖一定存在断层线
例二:幻方
\(n\)阶幻方中所有整数的和是:
上面的和利用了算术级数的求和公式
\(n\)阶幻方有\(n\)行,且幻和是\(s\),则有\(ns=\frac{n^2(n^2+1)}{2}\),因此,任意两个\(n\)阶幻方都有相同的幻和,即
幻方的一种构造方法:
\(n\)是奇数时
\(1.\)先把\(1\)放在第一行的中间
\(2.\)放好一个数后的下一个数放在当前数字的右上方
\(3.\)若右上方已有数字,则放入正下方
三阶幻方满足的性质:
与这个立方体的边平行的直线、每个平面截面的两条对角线、四条空间对角线的幻和相等
\(s=\frac{n^4+n}{2}\),下面证明不存在三阶幻方体:
如果存在,那么幻和\(s=42\)。考虑任意\(3*3\)截面
根据幻方体定义,有
前三个式子相加减去后两个等式后得到\(y=14\),说明每个截面的中心都必须是\(14\),而幻方中只能填入一个\(14\),所以不存在三阶幻方体
例三:四色问题
相邻国家不同色的染色问题,已经证明最多五种颜色可以给任何一张地图染色,且目前依靠计算机计算可以证明仅用四种颜色可以给每一张平面地图染色
例四:36军官问题
给定来自\(6\)种军衔和\(6\)个军团的\(36\)名军官,能不能把他们排列成一个\(6*6\)的编队,使得每一行和每一列上满足每个军衔有一名军官且每个军团有一名军官呢?
可以给一名军官指定一个有序对\((i,j)\),其中\(i(i=1,2,…6)\)表示他的军衔,\(j(j=1,2,…6)\)表示他的军团,于是这个问题要问:
能不能把这\(36\)个有序对\((i,j)\)排列成一个\(6*6\)的矩阵,使得每一行和每一列上整数\(1,2,…,6\)都能以某种顺序出现在有序对的第一个位置上,且都能以某种顺序出现在有序对的第二个位置上?
我们可以把这样的矩阵分割成两个\(6*6\)的矩阵,其中一个对应\(i\),另一个对应\(j\),
问题又可以变为,是否存在两个\(6*6\)的矩阵,它们的项都取自于整数\(1,2,…,6\),使得
\(1.\)在这两个矩阵种的每一行和每一列上整数\(1,2,…,6\)都能以某种顺序出现
\(2.\)当并置这两个矩阵时,所有有序对\((i,j)\)全部出现
于是这个问题的一个解是
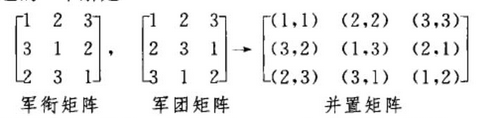
前面的军衔矩阵和军团矩阵是三阶拉丁方,整数\(1,2,3\)在每一行和每一列仅出现一次
这两个三阶拉丁方是正交的,因为当把它们并置时生成所有可能的\(9\)个有序对\((i,j)\)
所以问题可以改为研究:
存在两个六阶正交拉丁方吗?
至于这个问题后面再讨论(也可能不讨论了((
例五:最短路径问题
没说正经东西
例六:相互重叠的圆
设\(h_n\)等于构建的区域数,平凡地\(h_1\)=2,接下来有\(h_2=4,h_3=8\),因此猜测\(h_4=16\)
但下图证明\(h_4=14\)

解决这一类问题通常用增量法
设我们有\(h_{n-1}\),现在加入第\(n\)个圆,前\(n-1\)个圆与第\(n\)个圆每个最多有\(2\)个交点,所以会新产生最多\(2(n-1)\)个交点,这些交点第\(n\)个圆分割成\(2(n-1)\)条弧,每条弧都创建出一个新的区域,所以
例七:Nim游戏
\(n\)堆硬币,每堆硬币数量不等,玩家轮流每次至少从其中一堆硬币种取走至少一个硬币,取走最后一枚硬币的玩家获胜
先考虑仅有两堆的Nim游戏,后手可以保持永远让两堆数量相等来取胜
再推广到\(k\)堆,后手可以通过让每堆石子的所有二进制的每一位上加起来永远是偶数取胜


 浙公网安备 33010602011771号
浙公网安备 33010602011771号