LeetCode-矩阵对角线元素的和

题目

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

示例 1：

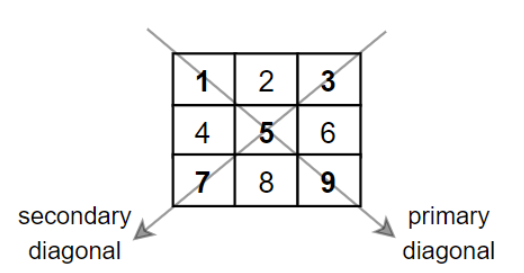
输入：mat = [[1,2,3],
[4,5,6],
[7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。
示例 2：

输入：mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]]
输出：8
示例 3：

输入：mat = [[5]]
输出：5

我的解答

class Solution {
    public int diagonalSum(int[][] mat) {
        int len=mat.length;
        int result=0;
        for(int i=0;i<len;i++){
            result+=mat[i][i];
        }
        for(int i=len-1;i>=0;i--){
            if(i==len-1-i){
                continue;
            }
            result+=mat[i][len-1-i];
        }
        return result;
    }
}

官方题解

方法一：遍历矩阵
思路与算法

我们知道矩阵中某个位置 (i,j) 处于对角线上，则一定满足下列条件之一：

i=j；
i+j=n−1；
根据上述结论，我们可以遍历整个矩阵，如果当前坐标 (i,j) 满足 i=j 或者 i+j=n−1 则表示该位置一定在对角线上，则把当前的数字加入到答案之中。

class Solution {
    public int diagonalSum(int[][] mat) {
        int n = mat.length, sum = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j || i + j == n - 1) {
                    sum += mat[i][j];
                }
            }
        }
        return sum;
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/matrix-diagonal-sum/solutions/441166/ju-zhen-dui-jiao-xian-yuan-su-de-he-by-leetcode-so/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

方法二：枚举对角线元素
思路与算法

逐行遍历，记当前的行号为 i，则当前行中处于对角线的元素为： 坐标 (i,i) 和坐标 (i,n−i−1)，因此我们把 (i,i) 与 (i,n−i−1) 处的数字加入到答案中。
如果 n 是奇数的话，则主对角线与副对角线存在交点 (⌊
2
n
​
⌋,⌊
2
n
​
⌋)，该点会被计算两次。所以当 n 为奇数的时候，需要减掉交点处的值。

class Solution {
    public int diagonalSum(int[][] mat) {
        int n = mat.length, sum = 0, mid = n / 2;
        for (int i = 0; i < n; ++i) {
            sum += mat[i][i] + mat[i][n - 1 - i];
        }
        return sum - mat[mid][mid] * (n & 1);
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/matrix-diagonal-sum/solutions/441166/ju-zhen-dui-jiao-xian-yuan-su-de-he-by-leetcode-so/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

思考

官方题解1中反对角线的坐标i+j=n-1，这是数学问题。
官方题解2中n&1，这是java的按位与问题。
两个问题，我都不清楚，遗忘的东西真的是太多了。
最近这段时间我一直在思考，有必要刷算法题吗？对工作来说没有任何帮助，但是今天隐隐有开窍的感觉，工作中的问题，可能大部分都是数学问题，最后可能真的得去深入学习数学。