素数

素数又称质数。所谓素数是指除了 1 和它本身以外，不能被任何整数整除的数，例如17就是素数，因为它不能被 2~16 的任一整数整除。

思路1)：因此判断一个整数m是否是素数，只需把 m 被 2 ~ m-1 之间的每一个整数去除，如果都不能被整除，那么 m 就是一个素数。

思路2)：另外判断方法还可以简化。m 不必被 2 ~ m-1 之间的每一个整数去除，只需被 2 ~ 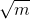 根号m之间的每一个整数去除就可以了。如果 m 不能被 2 ~ 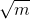根号m 间任一整数整除，m 必定是素数。例如判别 17 是是否为素数，只需使 17 被 2~4 之间的每一个整数去除，由于都不能整除，可以判定 17 是素数。

原因：因为如果 m 能被 2 ~ m-1 之间任一整数整除，其二个因子必定有一个小于或等于 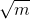，另一个大于或等于 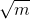。例如 16 能被 2、4、8 整除，16=2*8，2 小于 4，8 大于 4，16=4*4，4=√16，因此只需判定在 2~4 之间有无因子即可。

/*输出1到n之间的素数*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int pansu(int m)
{
	int flag = 0;
	for (int i=1; i<=(int)sqrt((float)m); i++)
	{
		//printf("%d\n", m % i);
		if ((m%i)==0)
		{
			flag++;
		}
		else
			continue;
	}
	if (flag==1)
		printf("%d\n", m);
	return 0;
}

int main()
{
	int n;
	scanf_s("%d", &n);
	for (int i = 1; i <= n; i++)
		pansu(i);
	return 0;
}

　　注意1不是素数，需要将其排除