OO第二次博客作业

OO第二次博客作业（PTA第四次、第五次作业及期中考试）

一、作业总结

　　作业四：作业四整体上难度适中，7-1和7-3难度较小，7-1重点考察同学审题的能力和对正则表达式的熟练度，7-3考察基本的设计类的能力，这两道题的通过率也很高，后面不做赘述。本次作业的难点集中在7-2凸四边形的计算上，本题也是“多边形系列”的题，不仅考察同学关于四边形相关问题的思考能力，还检验同学是否真正理解了面向对象设计的思想，想要做好这道题，需要将之前的三角形类设计好并且没有bug，而本题的四边形类也要设计的便于使用，因为作业五也需要用到，所以下面会重点介绍如何设计好类。

　　作业五：本次作业作为“多边形系列”的最终篇，可以说也是坑很多，非常考验同学对类的设计能力，如果之前的三角形类和四边形类没有设计好的话，做起来可以说很困难，所以想要“舒服”地搞定这道题，还是要稳扎稳打，从点到线到三角形到四边形，每一个类都要设计的很有逻辑。

　　期中考试：本次考试相较于之前折磨同学很久的“多边形系列”，可以说难度下降了不知道多少个档次，基本没有需要动脑子思考的部分，只考验同学明不明白“多态”的基本使用即可，只要对多态部分的知识学的比较扎实的话，相信对于同学们来说难度很低，后续也简单介绍一下多态的基本知识。

二、设计与分析

7-2 点线形系列4-凸四边形的计算：　　

用户输入一组选项和数据，进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

点击查看题目

　　分析：“多边形系列”题目的共同点就在于要“层层递进”，从点到线到三角形，每个类都要设计的很有逻辑，才能大幅降低后续更复杂的问题，这里先贴一下我的点Point，线Line，三角形triangle类：

 1  @SuppressWarnings("all")
 2     class Point {
 3 
 4         private double x;
 5         private double y;
 6 
 7         @Override
 8         public String toString() {
 9            /* if(x == -0.0)
10                 x = 0.0;
11              if(y == -0.0)
12                 y = 0.0;
13             */
14             return x + "," + y;
15         }
16 
17         public Point(double x, double y) {
18             this.x = x;
19             this.y = y;
20         }
21 
22         public double getX() {
23             return x;
24         }
25 
26         public void setX(double x) {
27             this.x = x;
28         }
29 
30         public double getY() {
31             return y;
32         }
33 
34         public void setY(double y) {
35             this.y = y;
36         }
37 
38         public double distance(Point point) {
39 
40             return Math.sqrt((x - point.x) * (x - point.x) + (y - point.y) * (y - point.y));
41         }
42 
43         @Override
44         public boolean equals(Object obj) {
45             Point obj1 = (Point) obj;
46             if (obj1.getX() == this.x && this.y == obj1.getY())
47                 return true;
48             else
49                 return false;
50 
51         }
52     }

点击查看Point类

　　里面存储了点的x和y两个二维坐标以及一些基本的获取与设置信息的方法和distance（Point p）{求与p点的距离}方法，以及重写了祖宗类Object的tostring方法和equals方法，方便后续进行输出和比较

  1 @SuppressWarnings("all")
  2 class Line {
  3     private double k = 0;
  4     private double yd;
  5     private boolean nok = false;
  6     private double x;
  7     public double a;
  8     public double b;
  9     public double c;
 10     public Point A;
 11     public Point B;
 12 
 13     public double getK() {
 14 
 15         return k;
 16     }
 17 
 18     public double getYd() {
 19         return yd;
 20     }
 21 
 22     public Line(Point p1, Point p2) {
 23         this.a = p1.getY() - p2.getY();
 24         this.b = p2.getX() - p1.getX();
 25         this.c = p1.getX() * p2.getY() - p2.getX() * p1.getY();
 26         if ((p1.getX() - p2.getX()) == 0) {
 27             nok = true;
 28             x = p1.getX();
 29             k = Double.NaN;
 30 
 31             if (p1.getY() > p2.getY()) {
 32                 A = p2;
 33                 B = p1;
 34             } else {
 35                 A = p1;
 36                 B = p2;
 37             }
 38         } else {
 39             this.k = -(a / b);
 40             this.yd = -(c / b);
 41             if (p1.getX() < p2.getX()) {
 42                 A = p1;
 43                 B = p2;
 44             } else {
 45                 A = p2;
 46                 B = p1;
 47 
 48             }
 49 
 50         }
 51     }
 52 
 53     public double getX(double y) {
 54 
 55 
 56         return -((c + b * y) / a);
 57     }
 58 
 59     public double getY(double x) {
 60 
 61 
 62         return -((c + a * x) / b);
 63     }
 64 
 65     public double distance(Point p) {
 66 
 67 
 68         double mol = Math.abs(a * p.getX() + b * p.getY() + c);
 69         double den = Math.sqrt(a * a + b * b);
 70         return mol / den;
 71     }
 72 
 73     public boolean isParallel(Line line) {
 74 
 75         if (Math.abs(a * line.b - b * line.a) < 0.000001)
 76             return true;
 77         else
 78             return false;
 79 
 80     }
 81 
 82     public boolean isOne(Line line) {
 83         if (!isParallel(line))
 84             return false;
 85         else {
 86             if (Math.abs(a * line.c - line.a * c) < 0.00001 && Math.abs(a * line.b - line.a * b) < 0.00001 && Math.abs(b * line.c - line.b * c) < 0.00001)
 87                 return true;
 88             else
 89                 return false;
 90         }
 91 
 92     }
 93 
 94     public double seglen() {
 95 
 96         return A.distance(B);
 97     }
 98 
 99 
100     public boolean isOnSeg(Point p) {
101 
102         if (!isOn(p))
103             return false;
104 
105         if (!nok) {
106 
107             if (p.getX() >= A.getX() && p.getX() <= B.getX())
108                 return true;
109             else return false;
110         } else {
111 
112             if (p.getY() >= A.getY() && p.getY() <= B.getY())
113                 return true;
114             else return false;
115 
116         }
117 
118     }
119 
120     public boolean isOnSegRan(Point p) {
121         if (!nok) {
122 
123             if (p.getX() >= A.getX() && p.getX() <= B.getX())
124                 return true;
125             else return false;
126         } else {
127 
128             if (p.getY() >= A.getY() && p.getY() <= B.getY())
129                 return true;
130             else return false;
131 
132         }
133 
134     }
135 
136     public boolean isOn(Point p) {
137 
138         if (nok) {
139             if (p.getX() == this.x)
140                 return true;
141             else
142                 return false;
143         }
144         double t = getY(p.getX());
145         if (Math.abs(t - p.getY()) < 0.000001)
146             return true;
147         else
148             return false;
149 
150     }
151 
152     public Point point(Line line) {
153 
154         double x, y;
155         x = (c * line.b - line.c * b) / (line.a * b - a * line.b);
156         y = (a * line.c - line.a * c) / (line.a * b - a * line.b);
157 
158 
159         return new Point(x, y);
160 
161     }
162 
163 
164     public static boolean isLine(Point a, Point b) {
165 
166         if (a.getX() == b.getX() && a.getY() == b.getY())
167             return false;
168         else
169             return true;
170     }
171 
172     public static boolean isColl(Point p1, Point p2, Point p3) {
173         if (p1.equals(p2)) {
174             return true;
175         } else {
176             Line line = new Line(p1, p2);
177             if (line.isOn(p3)) {
178                 return true;
179             } else
180                 return false;
181 
182         }
183 
184     }
185 }

点击查看Line类

　　线类的构造方法需要两个点（两点组成一条线），前提是两点不能重复，所以需要在创建Line对象时进行判断两点是否相同，如若相同就不可以创建对象；线的属性有组成该线的两个点A和B（该线类不仅可以表达直线，也可以表示一条线段），组成一条直线的各个参数（这里推荐使用直线的一般式ax+by+c=0来表示直线，可以避免很多情况的讨论）a，b，c，由于我一开始使用的是y=kx+b来表示，需要对x=k这一斜率不存在的直线单独考虑，出现了很多错误，后续更改为一般式的时候，也没有完全作废掉原来的，所以我的Line类有些冗余，里面还保留了k（斜率），nok（表示斜率是否存在），x（就是斜率不存在时，x=k里面的k），特此提醒；线的方法可以很丰富，甚至在后续三角形、四边形等类中为了方便其设计，还要在Line类里面添加新的方法，所以，方法这一块可以很多，这里只列举几个常用的方法getX(double y)和getY(double x)，给定x（或者y），来求直线上改点对应的y（或者x）， distance(Point p)求直线到p点的距离，isParallel(Line line)该直线是否与line直线平行，isOne(Line line)该直线是否与line直线是同一条直线，seglen()返回该线段的长度，isOnSeg(Point p)p点是否处于该线段上，isOn(Point p)p点是否处于该直线上，Point point(Line line)求两直线交点。

  1 @SuppressWarnings("all")
  2 class triangle extends Shape {
  3 
  4     Point A, B, C;
  5     Line AB, AC, BC;
  6 
  7     public triangle(Point a, Point b, Point c) {
  8         if (!triangle.isTriangle(a, b, c))
  9             return;
 10         A = a;
 11         B = b;
 12         C = c;
 13         AB = new Line(a, b);
 14         AC = new Line(a, c);
 15         BC = new Line(b, c);
 16     }
 17 
 18     public static boolean isTriangle(Point a, Point b, Point c) {
 19 
 20         if (!Line.isLine(a, b)) {
 21 
 22             return false;
 23         }
 24 
 25         Line line = new Line(a, b);
 26         if (line.isOn(c)) {
 27 
 28             return false;
 29         } else
 30             return true;
 31 
 32     }
 33 
 34     public double per() {
 35 
 36         return A.distance(B) + B.distance(C) + A.distance(C);
 37     }
 38 
 39     public double area() {
 40 
 41         double h = AB.distance(C);
 42         return h * A.distance(B) / 2;
 43 
 44     }
 45 
 46     @Override
 47     public double perimeter() {
 48         return AB.seglen() + AC.seglen() + BC.seglen();
 49     }
 50 
 51     public Point core() {
 52 
 53         double x = (A.getX() + B.getX() + C.getX()) / 3;
 54         double y = (A.getY() + B.getY() + C.getY()) / 3;
 55         return new Point(x, y);
 56     }
 57 
 58     public boolean isIn(Point p) {
 59 
 60         double d1 = (AB.seglen() * AB.distance(p)) / 2;
 61         double d2 = (AC.seglen() * AC.distance(p)) / 2;
 62         double d3 = (BC.seglen() * BC.distance(p)) / 2;
 63 
 64 
 65         if (Math.abs(d1 + d2 + d3 - this.area()) < 0.00001) {
 66             return true;
 67         } else {
 68             return false;
 69         }
 70     }
 71 
 72     public int cutting(Line line, double[] ds, Point[] ps) {
 73         if (this.AB.isOne(line) || this.BC.isOne(line) || this.AC.isOne(line)) {
 74 
 75             return -1;
 76         }
 77         Point p1 = null, p2 = null, p3 = null, tool = null;
 78 
 79         if (this.AB.isParallel(line)) {
 80             p1 = null;
 81         } else {
 82             tool = this.AB.point(line);
 83             if (this.AB.isOnSeg(tool)) {
 84                 p1 = tool;
 85             } else
 86                 p1 = null;
 87         }
 88         if (this.BC.isParallel(line)) {
 89             p2 = null;
 90         } else {
 91             tool = this.BC.point(line);
 92             if (this.BC.isOnSeg(tool)) {
 93                 p2 = tool;
 94             } else
 95                 p2 = null;
 96         }
 97         if (this.AC.isParallel(line)) {
 98             p3 = null;
 99         } else {
100             tool = this.AC.point(line);
101             if (this.AC.isOnSeg(tool)) {
102                 p3 = tool;
103             } else
104                 p3 = null;
105         }
106 
107         if (p1 == null && p2 == null && p3 == null) {
108             return 0;
109         }
110         if (p1 == null) {
111             if (p2.equals(p3)) {
112                 return 1;
113             } else {
114 
115                 double d1 = new triangle(p2, p3, this.C).area();
116                 double d2 = this.area() - d1;
117                 ps[0] = this.C;
118                 ps[1] = null;
119                 ds[0] = d1;
120                 ds[1] = d2;
121                 return 2;
122             }
123         }
124         if (p2 == null) {
125             if (p1.equals(p3)) {
126                 return 1;
127             } else {
128 
129                 double d1 = new triangle(p1, p3, this.A).area();
130                 double d2 = this.area() - d1;
131                 ps[0] = this.A;
132                 ps[1] = null;
133                 ds[0] = d1;
134                 ds[1] = d2;
135                 return 2;
136             }
137         }
138         if (p3 == null) {
139             if (p1.equals(p2)) {
140                 return 1;
141             } else {
142 
143                 double d1 = new triangle(p1, p2, this.B).area();
144                 double d2 = this.area() - d1;
145                 ps[0] = this.B;
146                 ps[1] = null;
147                 ds[0] = d1;
148                 ds[1] = d2;
149                 return 2;
150             }
151         }
152 
153 
154         if (p1.equals(p2)) {
155 
156             double d1 = new triangle(this.A, this.B, p3).area();
157             double d2 = this.area() - d1;
158 
159             ps[0] = this.A;
160             ps[1] = this.C;
161             ds[0] = d1;
162             ds[1] = d2;
163 
164         }
165         if (p1.equals(p3)) {
166 
167             double d1 = new triangle(this.A, p2, this.C).area();
168             double d2 = this.area() - d1;
169             ps[0] = this.C;
170             ps[1] = this.B;
171             ds[0] = d1;
172             ds[1] = d2;
173         }
174         if (p2.equals(p3)) {
175 
176             double d1 = new triangle(p1, this.C, this.A).area();
177             double d2 = this.area() - d1;
178             ps[0] = this.A;
179             ps[1] = this.B;
180             ds[0] = d1;
181             ds[1] = d2;
182         }
183         return 2;
184     }
185 
186 }

点击查看triangle类

　　Triangle类的构造方法需要三个点，属性有三个点A，B，C和三条边AB，BC，AC，方法也同Line类，可以不断丰富完善，boolean isTriangle(Point a, Point b, Point c)三点能否组成一线，double per()，public double area(), public Point core() 返回三角形的周长，面积和重心坐标

　　接下来设计我们本次要用到的四边形类，其属性有四个点以及四条边，方法可以有很多很多，每个同学也可以玩出不同的花样，比如求面积、周长，与直线的切割方法等：

  1 @SuppressWarnings("all")
  2 class Quadrangle extends Shape {
  3 
  4     Point A;
  5     Point B;
  6     Point C;
  7     Point D;
  8     Line AB;
  9     Line BC;
 10     Line CD;
 11     Line DA;
 12 
 13     public int cutting(Line line, double[] ds, Point[] ps) {
 14 
 15 
 16         if (this.AB.isOne(line) || this.BC.isOne(line) || this.CD.isOne(line) || this.DA.isOne(line)) {
 17             return -1;
 18         }
 19         double[] ds1 = new double[2];
 20         Point[] ps1 = new Point[2];
 21         double[] ds2 = new double[2];
 22         Point[] ps2 = new Point[2];
 23         triangle t1 = new triangle(this.A, this.B, this.D);
 24         triangle t2 = new triangle(this.B, this.C, this.D);
 25         int i1 = t1.cutting(line, ds1, ps1);
 26         int i2 = t2.cutting(line, ds2, ps2);
 27         Line l = new Line(this.B, this.D);
 28         Line ll = new Line(this.A, this.C);
 29         if (l.isOne(line)) {
 30 
 31             ds[0] = t1.area();
 32             ds[1] = t2.area();
 33             ps[0] = B;
 34             ps[1] = D;
 35             return 2;
 36         }
 37         if (ll.isOne(line)) {
 38             ds[0] = new triangle(this.A, this.C, this.B).area();
 39             ds[1] = new triangle(this.A, this.C, this.D).area();
 40             ps[0] = A;
 41             ps[1] = C;
 42             return 2;
 43 
 44         }
 45         if (i1 == 0 && i2 == 0) {
 46             return 0;
 47         }
 48         if (i1 == 1 && i2 == 1) {
 49             return 1;
 50         }
 51         if (i1 + i2 == 1) {
 52             return 1;
 53         }
 54         if (i1 == 2) {
 55 
 56             if (i2 == 0) {
 57 
 58                 double d1 = ds1[0];
 59                 double d2 = ds1[1] + t2.area();
 60                 ds[0] = d1;
 61                 ds[1] = d2;
 62                 ps[0] = null;
 63                 ps[1] = null;
 64 
 65 
 66             }
 67             if (i2 == 1) {
 68                 if (ps1[0].equals(this.A)) {
 69                     double d1 = ds1[0];
 70                     double d2 = ds1[1] + t2.area();
 71                     ds[0] = d1;
 72                     ds[1] = d2;
 73                     ps[0] = null;
 74                     ps[1] = null;
 75                 } else {
 76                     double d1 = ds1[1];
 77                     double d2 = ds1[0] + t2.area();
 78                     ds[0] = d1;
 79                     ds[1] = d2;
 80                     ps[0] = null;
 81                     ps[1] = null;
 82                 }
 83             }
 84              if (ps1[1] != null && ps2[1] == null) {
 85                     ps[0] = ps2[0];
 86                     ps[1] = null;
 87                     if (ps1[0].equals(ps2[0])) {
 88                         double d1 = ds1[0] + ds2[0];
 89                         double d2 = this.area() - d1;
 90                         ds[0] = d1;
 91                         ds[1] = d2;
 92                     } else {
 93                         double d1 = ds1[1] + ds2[0];
 94                         double d2 = this.area() - d1;
 95                         ds[0] = d1;
 96                         ds[1] = d2;
 97                     }
 98                 }
 99                 //134 233
100                 if (ps1[1] == null && ps2[1] != null){
101                     ps[0] = ps1[0];
102                     ps[1] = null;
103                     if (ps2[0].equals(ps1[0])) {
104                         double d1 = ds1[0] + ds2[0];
105                         double d2 = this.area() - d1;
106                         ds[0] = d1;
107                         ds[1] = d2;
108                     } else {
109                         double d1 = ds1[0] + ds2[1];
110                         double d2 = this.area() - d1;
111                         ds[0] = d1;
112                         ds[1] = d2;
113                     }
114                     
115                 }
116                 
117                 //134 234
118                 if(ps1[1] == null&&ps2[1] == null){
119                     
120                     if(ps1[0].equals(this.B)&&ps2[0].equals(this.B)){
121                         ps[0] = B;
122                         ps[1] = null;
123                         double d1 = ds1[0] + ds2[0];
124                         double d2 = this.area() - d1;
125                         ds[0] = d1;
126                         ds[1] = d2;
127                     }
128                     if(ps1[0].equals(this.D)&&ps2[0].equals(this.D)){
129                         ps[0] = D;
130                         ps[1] = null;
131                         double d1 = ds1[0] + ds2[0];
132                         double d2 = this.area() - d1;
133                         ds[0] = d1;
134                         ds[1] = d2;
135                     }
136                     if(ps1[0].equals(this.B)&&ps2[0].equals(this.D)){
137                         ps[0] = B;
138                         ps[1] = C;
139                         double d1 = ds1[0] + ds2[1];
140                         double d2 = this.area() - d1;
141                         ds[0] = d1;
142                         ds[1] = d2;
143                     }
144                     if(ps1[0].equals(this.D)&&ps2[0].equals(this.B)){
145                         ps[0] = A;
146                         ps[1] = B;
147                         double d1 = ds1[1] + ds2[0];
148                         double d2 = this.area() - d1;
149                         ds[0] = d1;
150                         ds[1] = d2;
151                     }
152                     
153                 }
154             return 2;
155         }
156         if (i2 == 2) {
157 
158             if (i1 == 0) {
159                 double d1 = ds2[0];
160                 double d2 = ds2[1] + t1.area();
161                 ds[0] = d1;
162                 ds[1] = d2;
163                 ps[0] = null;
164                 ps[1] = null;
165             }
166             if (i1 == 1) {
167                 if (ps2[0].equals(this.C)) {
168                     double d1 = ds2[0];
169                     double d2 = ds2[1] + t1.area();
170                     ds[0] = d1;
171                     ds[1] = d2;
172                     ps[0] = null;
173                     ps[1] = null;
174                 } else {
175                     double d1 = ds2[1];
176                     double d2 = ds2[0] + t1.area();
177                     ds[0] = d1;
178                     ds[1] = d2;
179                     ps[0] = null;
180                     ps[1] = null;
181                 }
182             }
183             /*
184                  if (i1 == 2) {
185                 if (ps2[1] == null) {
186                     if (ps1[0].equals(ps2[0])) {
187                         double d1 = ds1[0] + ds2[0];
188                         double d2 = this.area() - d1;
189                         ds[0] = d1;
190                         ds[1] = d2;
191                         ps[0] = null;
192                         ps[1] = null;
193                     } else {
194                         double d1 = ds1[1] + ds2[0];
195                         double d2 = this.area() - d1;
196                         ds[0] = d1;
197                         ds[1] = d2;
198                         ps[0] = null;
199                         ps[1] = null;
200                     }
201                 } else {
202                     if (ps2[0].equals(ps1[0])) {
203                         double d1 = ds1[0] + ds2[0];
204                         double d2 = this.area() - d1;
205                         ds[0] = d1;
206                         ds[1] = d2;
207                         ps[0] = null;
208                         ps[1] = null;
209                     } else {
210                         double d1 = ds1[0] + ds2[1];
211                         double d2 = this.area() - d1;
212                         ds[0] = d1;
213                         ds[1] = d2;
214                         ps[0] = null;
215                         ps[1] = null;
216                     }
217                 }
218 
219             }
220             */
221        
222             return 2;
223         }
224         return 5;
225     }
226 
227     public Quadrangle(Point a, Point b, Point c, Point d) {
228         A = a;
229         B = b;
230         C = c;
231         D = d;
232         AB = new Line(A, B);
233         BC = new Line(B, C);
234         CD = new Line(C, D);
235         DA = new Line(D, A);
236     }
237 
238     //0-非四边形，1-普通四边形，2-平行四边形
239     public static int shape1(Point p1, Point p2, Point p3, Point p4) {
240 
241         if (p1.equals(p2) || p1.equals(p3) || p1.equals(p4) || p2.equals(p3) || p2.equals(p4) || p3.equals(p4)) {
242             return 0;
243         }
244 
245         Line line1 = new Line(p1, p2);
246         if (line1.isOn(p3) || line1.isOn(p4)) {
247             return 0;
248         }
249 
250         Line line2 = new Line(p2, p3);
251         if (line2.isOn(p1) || line2.isOn(p4)) {
252 
253             return 0;
254         }
255 
256         Line line3 = new Line(p3, p4);
257         if (line3.isOn(p1) || line3.isOn(p2)) {
258             return 0;
259         }
260 
261         Line line4 = new Line(p1, p4);
262         if (line4.isOn(p2) || line4.isOn(p3)) {
263             return 0;
264         }
265 
266         if (!line4.isParallel(line2)) {
267             Point p = line4.point(line2);
268             if (line4.isOnSeg(p) && line2.isOnSeg(p))
269                 return 0;
270         }
271         if (!line1.isParallel(line3)) {
272             Point p = line1.point(line3);
273             if (line1.isOnSeg(p) && line3.isOnSeg(p))
274                 return 0;
275         }
276         if (line1.isParallel(line3) && line1.seglen() == line3.seglen())
277             return 2;
278 
279 
280         return 1;
281     }
282 
283     //0-不是平行四边形,1-菱形,2-矩形,3-正方形,4-普通平行四边形
284     public static int shape2(Point p1, Point p2, Point p3, Point p4) {
285 
286         if (shape1(p1, p2, p3, p4) != 2) {
287             return 0;
288         }
289 
290         Line l1 = new Line(p1, p2);
291         Line l2 = new Line(p2, p3);
292         Line l3 = new Line(p3, p4);
293         Line l4 = new Line(p1, p4);
294         Line l5 = new Line(p1, p3);
295         if (l1.seglen() == l2.seglen()) {
296             if (Math.abs(Math.pow(l1.seglen(), 2) + Math.pow(l2.seglen(), 2) - Math.pow(l5.seglen(), 2)) < 0.00001) {
297 
298                 return 3;
299             } else {
300 
301                 return 1;
302             }
303 
304 
305         }
306 
307         if (Math.abs(Math.pow(l1.seglen(), 2) + Math.pow(l2.seglen(), 2) - Math.pow(l5.seglen(), 2)) < 0.00001)
308             return 2;
309         else
310             return 4;
311     }
312 
313     //判断是否可以组成三角形
314     public static triangle shape3(Point p1, Point p2, Point p3, Point p4) {
315 
316         if (p1.equals(p2) && p1.equals(p3) && p1.equals(p4) && p2.equals(p3)) {
317             return null;
318         }
319 
320         if (p1.equals(p2)) {
321             if (triangle.isTriangle(p1, p3, p4)) {
322                 return new triangle(p1, p3, p4);
323             }
324         }
325         if (p1.equals(p3)) {
326             if (triangle.isTriangle(p1, p2, p4)) {
327                 return new triangle(p1, p2, p4);
328             }
329         }
330         if (p1.equals(p4)) {
331             if (triangle.isTriangle(p1, p2, p3)) {
332                 return new triangle(p1, p2, p3);
333             }
334         }
335         if (p2.equals(p3)) {
336             if (triangle.isTriangle(p1, p3, p4)) {
337                 return new triangle(p1, p3, p4);
338             }
339         }
340         if (p2.equals(p4)) {
341             if (triangle.isTriangle(p1, p3, p4)) {
342                 return new triangle(p1, p3, p4);
343             }
344         }
345         if (p3.equals(p4)) {
346             if (triangle.isTriangle(p1, p2, p3)) {
347                 return new triangle(p1, p2, p3);
348             }
349         }
350 
351         if (!p1.equals(p2)) {
352             if (Line.isColl(p1, p2, p3) && Line.isColl(p1, p2, p4))
353                 return null;
354         }
355         if (!p2.equals(p3)) {
356             if (Line.isColl(p1, p2, p3) && Line.isColl(p3, p2, p4))
357                 return null;
358         }
359         if (!p3.equals(p4)) {
360             if (Line.isColl(p1, p4, p3) && Line.isColl(p3, p2, p4))
361                 return null;
362         }
363         if (!p1.equals(p4)) {
364             if (Line.isColl(p1, p2, p4) && Line.isColl(p1, p3, p4))
365                 return null;
366         }
367 
368 
369         if (Line.isColl(p1, p2, p3)) {
370 
371             Line l = new Line(p1, p3);
372             if (l.isOnSeg(p2)) {
373                 return new triangle(p1, p3, p4);
374             } else
375                 return null;
376 
377         }
378         if (Line.isColl(p1, p2, p4)) {
379 
380             Line l = new Line(p2, p4);
381             if (l.isOnSeg(p1)) {
382                 return new triangle(p2, p3, p4);
383             } else
384                 return null;
385 
386         }
387         if (Line.isColl(p2, p3, p4)) {
388 
389             Line l = new Line(p2, p4);
390             if (l.isOnSeg(p3)) {
391                 return new triangle(p1, p2, p4);
392             } else
393                 return null;
394 
395         }
396         if (Line.isColl(p1, p3, p4)) {
397 
398             Line l = new Line(p1, p3);
399             if (l.isOnSeg(p4)) {
400                 return new triangle(p1, p2, p3);
401             } else
402                 return null;
403 
404         }
405 
406 
407         return null;
408     }
409 
410 
411     //是否为凹
412     public boolean isConcave() {
413 
414         double d1 = new triangle(A, B, C).area();
415         double d2 = new triangle(A, D, C).area();
416         double d3 = new triangle(B, A, D).area();
417         double d4 = new triangle(B, C, D).area();
418         if (Math.abs(d1 + d2 - d3 - d4) < 0.00001)
419             return false;
420         else
421             return true;
422 
423     }
424 
425     public double perimeter() {
426         Line l1 = new Line(A, B);
427         Line l2 = new Line(B, C);
428         Line l3 = new Line(C, D);
429         Line l4 = new Line(D, A);
430         return l1.seglen() + l2.seglen() + l3.seglen() + l4.seglen();
431 
432     }
433 
434     public double area() {
435         double d1 = new triangle(A, B, C).area();
436         double d2 = new triangle(A, D, C).area();
437         double d3 = new triangle(B, A, D).area();
438         double d4 = new triangle(B, C, D).area();
439         double s1 = d1 + d2;
440         double s2 = d3 + d4;
441         if (Math.abs(s1 - s2) < 0.00001)
442             return s1;
443         else {
444             if (s1 < s2)
445                 return s1;
446             else
447                 return s2;
448         }
449 
450     }
451 
452     public static double qualArea(Point p1, Point p2, Point p3, Point p4) {
453 
454         triangle t = Quadrangle.shape3(p1, p2, p3, p4);
455         if (t == null)
456             return new Quadrangle(p1, p2, p3, p4).area();
457         else
458             return t.area();
459 
460     }
461 
462 
463 }

点击查看四边形Quadrangle类

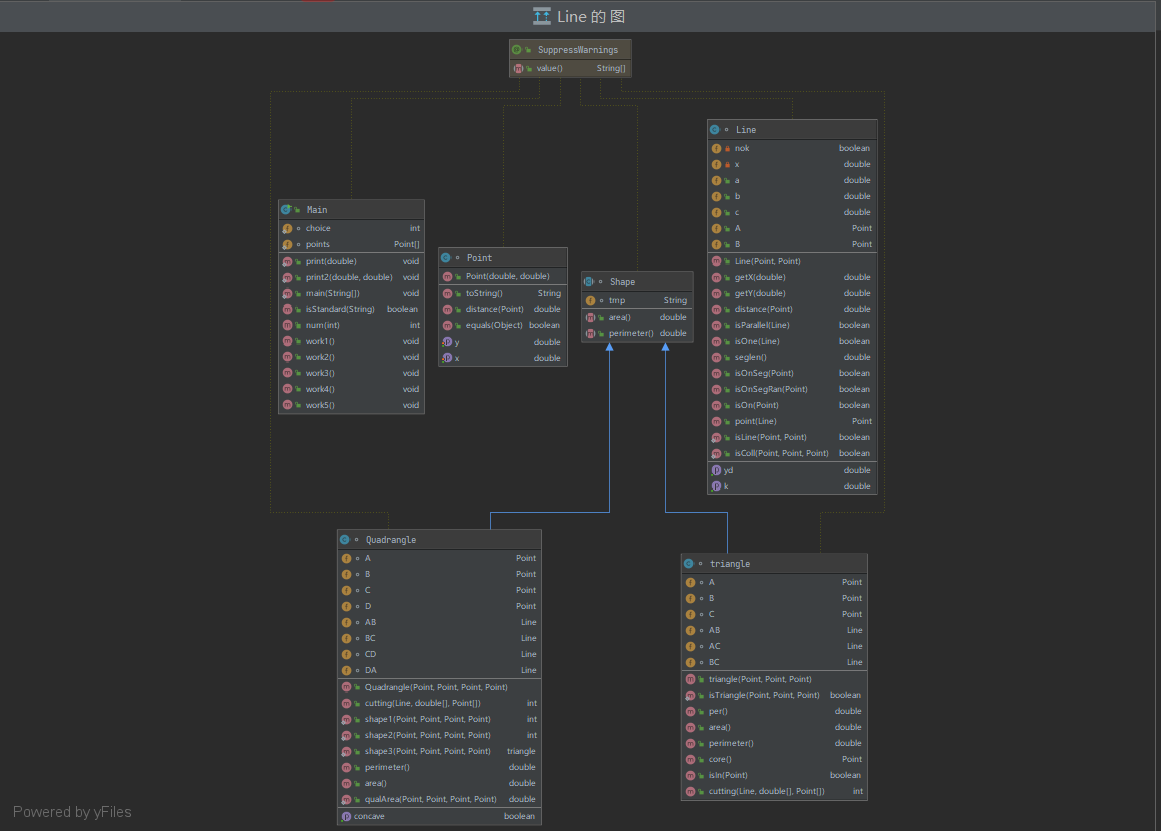
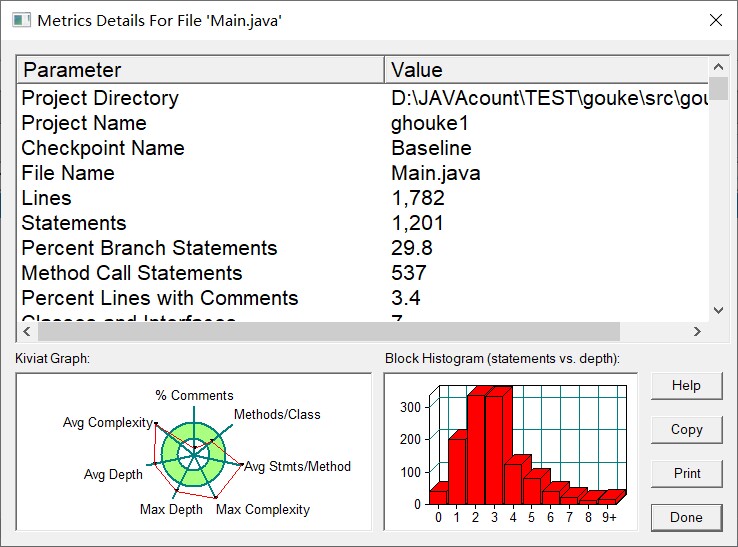
　　　　选项一判断四个点能不能组成四边形，原理就是不能出现三、四点共线（重复点也不行）以及非邻边不能有交点：

 1  //0-非四边形，1-普通四边形，2-平行四边形
 2     public static int shape1(Point p1, Point p2, Point p3, Point p4) {
 3 
 4         if (p1.equals(p2) || p1.equals(p3) || p1.equals(p4) || p2.equals(p3) || p2.equals(p4) || p3.equals(p4)) {
 5             return 0;
 6         }
 7 
 8         Line line1 = new Line(p1, p2);
 9         if (line1.isOn(p3) || line1.isOn(p4)) {
10             return 0;
11         }
12 
13         Line line2 = new Line(p2, p3);
14         if (line2.isOn(p1) || line2.isOn(p4)) {
15 
16             return 0;
17         }
18 
19         Line line3 = new Line(p3, p4);
20         if (line3.isOn(p1) || line3.isOn(p2)) {
21             return 0;
22         }
23 
24         Line line4 = new Line(p1, p4);
25         if (line4.isOn(p2) || line4.isOn(p3)) {
26             return 0;
27         }
28 
29         if (!line4.isParallel(line2)) {
30             Point p = line4.point(line2);
31             if (line4.isOnSeg(p) && line2.isOnSeg(p))
32                 return 0;
33         }
34         if (!line1.isParallel(line3)) {
35             Point p = line1.point(line3);
36             if (line1.isOnSeg(p) && line3.isOnSeg(p))
37                 return 0;
38         }
39         if (line1.isParallel(line3) && line1.seglen() == line3.seglen())
40             return 2;
41 
42 
43         return 1;
44 }

　　选项二判断是不是菱形、矩形、正方形，优先要通过选项一确定是四边形，然后根据四边的相等情况，以及勾股定理进行判断：

 1  //0-不是平行四边形,1-菱形,2-矩形,3-正方形,4-普通平行四边形
 2     public static int shape2(Point p1, Point p2, Point p3, Point p4) {
 3 
 4         if (shape1(p1, p2, p3, p4) != 2) {
 5             return 0;
 6         }
 7 
 8         Line l1 = new Line(p1, p2);
 9         Line l2 = new Line(p2, p3);
10         Line l3 = new Line(p3, p4);
11         Line l4 = new Line(p1, p4);
12         Line l5 = new Line(p1, p3);
13         if (l1.seglen() == l2.seglen()) {
14             if (Math.abs(Math.pow(l1.seglen(), 2) + Math.pow(l2.seglen(), 2) - Math.pow(l5.seglen(), 2)) < 0.00001) {
15 
16                 return 3;
17             } else {
18 
19                 return 1;
20             }
21 
22 
23         }
24 
25         if (Math.abs(Math.pow(l1.seglen(), 2) + Math.pow(l2.seglen(), 2) - Math.pow(l5.seglen(), 2)) < 0.00001)
26             return 2;
27         else
28             return 4;
29     }

　　　　选项三判断四边形凹凸性，原理连接两组对顶点，连线分别和另外两点组成两个三角形，如果两组三角形面积之和相等，则为凸四边形，反之为凹：

 1 //是否为凹
 2     public boolean isConcave() {
 3 
 4         double d1 = new triangle(A, B, C).area();
 5         double d2 = new triangle(A, D, C).area();
 6         double d3 = new triangle(B, A, D).area();
 7         double d4 = new triangle(B, C, D).area();
 8         if (Math.abs(d1 + d2 - d3 - d4) < 0.00001)
 9             return false;
10         else
11             return true;
12 
13     }

　　选项四最为麻烦，直线切割问题，首先进行判断是三角形还是四边形，三角形则调用三角形类之间封装切割方法即可，四边形就切割成两个三角形分别调用、根据返回信息进行判断即可，非常考验同学之前三角形类设计的能力

 1  //判断是否可以组成三角形
 2     public static triangle shape3(Point p1, Point p2, Point p3, Point p4) {
 3 
 4         if (p1.equals(p2) && p1.equals(p3) && p1.equals(p4) && p2.equals(p3)) {
 5             return null;
 6         }
 7 
 8         if (p1.equals(p2)) {
 9             if (triangle.isTriangle(p1, p3, p4)) {
10                 return new triangle(p1, p3, p4);
11             }
12         }
13         if (p1.equals(p3)) {
14             if (triangle.isTriangle(p1, p2, p4)) {
15                 return new triangle(p1, p2, p4);
16             }
17         }
18         if (p1.equals(p4)) {
19             if (triangle.isTriangle(p1, p2, p3)) {
20                 return new triangle(p1, p2, p3);
21             }
22         }
23         if (p2.equals(p3)) {
24             if (triangle.isTriangle(p1, p3, p4)) {
25                 return new triangle(p1, p3, p4);
26             }
27         }
28         if (p2.equals(p4)) {
29             if (triangle.isTriangle(p1, p3, p4)) {
30                 return new triangle(p1, p3, p4);
31             }
32         }
33         if (p3.equals(p4)) {
34             if (triangle.isTriangle(p1, p2, p3)) {
35                 return new triangle(p1, p2, p3);
36             }
37         }
38 
39         if (!p1.equals(p2)) {
40             if (Line.isColl(p1, p2, p3) && Line.isColl(p1, p2, p4))
41                 return null;
42         }
43         if (!p2.equals(p3)) {
44             if (Line.isColl(p1, p2, p3) && Line.isColl(p3, p2, p4))
45                 return null;
46         }
47         if (!p3.equals(p4)) {
48             if (Line.isColl(p1, p4, p3) && Line.isColl(p3, p2, p4))
49                 return null;
50         }
51         if (!p1.equals(p4)) {
52             if (Line.isColl(p1, p2, p4) && Line.isColl(p1, p3, p4))
53                 return null;
54         }
55 
56 
57         if (Line.isColl(p1, p2, p3)) {
58 
59             Line l = new Line(p1, p3);
60             if (l.isOnSeg(p2)) {
61                 return new triangle(p1, p3, p4);
62             } else
63                 return null;
64 
65         }
66         if (Line.isColl(p1, p2, p4)) {
67 
68             Line l = new Line(p2, p4);
69             if (l.isOnSeg(p1)) {
70                 return new triangle(p2, p3, p4);
71             } else
72                 return null;
73 
74         }
75         if (Line.isColl(p2, p3, p4)) {
76 
77             Line l = new Line(p2, p4);
78             if (l.isOnSeg(p3)) {
79                 return new triangle(p1, p2, p4);
80             } else
81                 return null;
82 
83         }
84         if (Line.isColl(p1, p3, p4)) {
85 
86             Line l = new Line(p1, p3);
87             if (l.isOnSeg(p4)) {
88                 return new triangle(p1, p2, p3);
89             } else
90                 return null;
91 
92         }
93 
94 
95         return null;
96     }

点击查看判断是否可以组成三角形的方法

  1  public int cutting(Line line, double[] ds, Point[] ps) {
  2         if (this.AB.isOne(line) || this.BC.isOne(line) || this.AC.isOne(line)) {
  3 
  4             return -1;
  5         }
  6         Point p1 = null, p2 = null, p3 = null, tool = null;
  7 
  8         if (this.AB.isParallel(line)) {
  9             p1 = null;
 10         } else {
 11             tool = this.AB.point(line);
 12             if (this.AB.isOnSeg(tool)) {
 13                 p1 = tool;
 14             } else
 15                 p1 = null;
 16         }
 17         if (this.BC.isParallel(line)) {
 18             p2 = null;
 19         } else {
 20             tool = this.BC.point(line);
 21             if (this.BC.isOnSeg(tool)) {
 22                 p2 = tool;
 23             } else
 24                 p2 = null;
 25         }
 26         if (this.AC.isParallel(line)) {
 27             p3 = null;
 28         } else {
 29             tool = this.AC.point(line);
 30             if (this.AC.isOnSeg(tool)) {
 31                 p3 = tool;
 32             } else
 33                 p3 = null;
 34         }
 35 
 36         if (p1 == null && p2 == null && p3 == null) {
 37             return 0;
 38         }
 39         if (p1 == null) {
 40             if (p2.equals(p3)) {
 41                 return 1;
 42             } else {
 43 
 44                 double d1 = new triangle(p2, p3, this.C).area();
 45                 double d2 = this.area() - d1;
 46                 ps[0] = this.C;
 47                 ps[1] = null;
 48                 ds[0] = d1;
 49                 ds[1] = d2;
 50                 return 2;
 51             }
 52         }
 53         if (p2 == null) {
 54             if (p1.equals(p3)) {
 55                 return 1;
 56             } else {
 57 
 58                 double d1 = new triangle(p1, p3, this.A).area();
 59                 double d2 = this.area() - d1;
 60                 ps[0] = this.A;
 61                 ps[1] = null;
 62                 ds[0] = d1;
 63                 ds[1] = d2;
 64                 return 2;
 65             }
 66         }
 67         if (p3 == null) {
 68             if (p1.equals(p2)) {
 69                 return 1;
 70             } else {
 71 
 72                 double d1 = new triangle(p1, p2, this.B).area();
 73                 double d2 = this.area() - d1;
 74                 ps[0] = this.B;
 75                 ps[1] = null;
 76                 ds[0] = d1;
 77                 ds[1] = d2;
 78                 return 2;
 79             }
 80         }
 81 
 82 
 83         if (p1.equals(p2)) {
 84 
 85             double d1 = new triangle(this.A, this.B, p3).area();
 86             double d2 = this.area() - d1;
 87 
 88             ps[0] = this.A;
 89             ps[1] = this.C;
 90             ds[0] = d1;
 91             ds[1] = d2;
 92 
 93         }
 94         if (p1.equals(p3)) {
 95 
 96             double d1 = new triangle(this.A, p2, this.C).area();
 97             double d2 = this.area() - d1;
 98             ps[0] = this.C;
 99             ps[1] = this.B;
100             ds[0] = d1;
101             ds[1] = d2;
102         }
103         if (p2.equals(p3)) {
104 
105             double d1 = new triangle(p1, this.C, this.A).area();
106             double d2 = this.area() - d1;
107             ps[0] = this.A;
108             ps[1] = this.B;
109             ds[0] = d1;
110             ds[1] = d2;
111         }
112         return 2;
113     }

点击查看直线切割三角形方法

　　如果是四边形，就切割进行分别调用：

 1  Quadrangle quadrangle = new Quadrangle(points[2], points[3], points[4], points[5]);
 2             double[] ds = new double[2];
 3             Point[] ps = new Point[2];
 4             int cutting = quadrangle.cutting(line, ds, ps);
 5             if (cutting == 0)
 6                 System.out.println("0");
 7             else if(cutting == 1)
 8                 System.out.println("1");
 9             else if(cutting == -1)
10                 System.out.println("The line is coincide with one of the lines");
11             else if(cutting == 2){
12                  System.out.print("2 ");
13                 print2(ds[0],ds[1]);
14             }

　　作业五：点线形系列5-凸五边形的计算

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。
以上3选项中，若输入的点无法构成多边形，则输出"not a polygon"。输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y
用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
4：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），判断它们两个之间是否存在包含关系（一个多边形有一条或多条边与另一个多边形重合，其他部分都包含在另一个多边形内部，也算包含）。
两者存在六种关系：1、分离（完全无重合点） 2、连接（只有一个点或一条边重合） 3、完全重合 4、被包含（前一个多边形在后一个多边形的内部）5、交错 6、包含（后一个多边形在前一个多边形的内部）。
各种关系的输出格式如下：
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），输出两个多边形公共区域的面积。注：只考虑每个多边形被另一个多边形分割成最多两个部分的情况，不考虑一个多边形将另一个分割成超过两个区域的情况。
6：输入六个点坐标，输出第一个是否在后五个点所构成的多边形（限定为凸多边形，不考虑凹多边形），的内部（若是五边形输出in the pentagon/outof the pentagon，若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。输入入错存在冗余点要排除，冗余点的判定方法见选项5。如果点在多边形的某条边上，输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

点击查看题目

　　由于选项四五六存在很多重复操作，可以创建一个工具类，进行集合-数组转化、对点进行顺逆时针排序（可以采用极坐标或者向量叉乘的几何含义进行判断），我采用的是向量叉乘

  1 @SuppressWarnings("all")
  2 class Tool {
  3 
  4     ArrayList<Point> arrp1;
  5     ArrayList<Point> arrp2;
  6     ArrayList<Line> arrl1;
  7     ArrayList<Line> arrl2;
  8 
  9     public Tool(ArrayList<Point> arrp1, ArrayList<Point> arrp2, ArrayList<Line> arrl1, ArrayList<Line> arrl2) {
 10         this.arrp1 = arrp1;
 11         this.arrp2 = arrp2;
 12         this.arrl1 = arrl1;
 13         this.arrl2 = arrl2;
 14     }
 15 
 16     public Point[] Unite() {
 17         ArrayList<Point> arr = new ArrayList<>();
 18         for (int i = 0; i < arrl1.size(); i++) {
 19             for (int j = 0; j < arrl2.size(); j++) {
 20                 if (!arrl1.get(i).isParallel(arrl2.get(j))) {
 21                     Point t = arrl1.get(i).point(arrl2.get(j));
 22                     if (arrl1.get(i).isOnSeg(t) && arrl2.get(j).isOnSeg(t) && Tool.isIn(t, Tool.to(arrp1)) != 0 && Tool.isIn(t, Tool.to(arrp2)) != 0)
 23                         arr.add(t);
 24                 }
 25             }
 26         }
 27         for (int i = 0; i < arrp1.size(); i++) {
 28             if (Tool.isIn(arrp1.get(i), Tool.to(arrp1)) != 0 && Tool.isIn(arrp1.get(i), Tool.to(arrp2)) != 0)
 29                 arr.add(arrp1.get(i));
 30         }
 31         for (int i = 0; i < arrp2.size(); i++) {
 32             if (Tool.isIn(arrp2.get(i), Tool.to(arrp1)) != 0 && Tool.isIn(arrp2.get(i), Tool.to(arrp2)) != 0)
 33                 arr.add(arrp2.get(i));
 34         }
 35 
 36         return Tool.to(arr);
 37     }
 38 
 39     public static int isIn(Point p, Point... x) {
 40         int i = 0;
 41         if (x.length == 3)
 42             i = new triangle(x[0], x[1], x[2]).isIn(p);
 43         if (x.length == 4)
 44             i = new Quadrangle(x[0], x[1], x[2], x[3]).isIn(p);
 45         if (x.length == 5)
 46             i = new Pentagon(x[0], x[1], x[2], x[3], x[4]).isIn(p);
 47         return i;
 48     }
 49 
 50     public static Point[] to(ArrayList arrayList) {
 51         Point[] ps = new Point[arrayList.size()];
 52         Object[] objects = arrayList.toArray();
 53         for (int i = 0; i < ps.length; i++) {
 54             ps[i] = (Point) objects[i];
 55         }
 56         return ps;
 57     }
 58 
 59 
 60     public static Point[] distinct(Point[] ps) {
 61         Point[] result = null, t = null;
 62         if (ps == null || ps.length == 0)
 63             return null;
 64         int i = 0;
 65         boolean flag = true;
 66         result = new Point[i + 1];
 67         result[i] = ps[i];
 68         i++;
 69         for (int j = 1; j < ps.length; j++) {
 70             flag = true;
 71             for (int k = 0; k < j; k++) {
 72                 if (ps[k].equals(ps[j])) {
 73                     flag = false;
 74                 }
 75             }
 76             if (flag) {
 77                 t = result;
 78                 result = new Point[i + 1];
 79                 result[i] = ps[j];
 80                 i++;
 81                 for (int k = 0; k < i - 1; k++) {
 82                     result[k] = t[k];
 83                 }
 84             }
 85         }
 86 
 87         return result;
 88     }
 89 
 90     //求叉乘值正负性
 91     public static double work(Point p, Point A, Point B) {
 92         double d = (A.getX() - p.getX()) * (B.getY() - p.getY()) - (B.getX() - p.getX()) * (A.getY() - p.getY());
 93         return d;
 94     }
 95 
 96     public static void sort(Point[] ps) {
 97 
 98         double x = 0, y = 0;
 99         for (int i = 0; i < ps.length; i++) {
100             x += ps[i].getX();
101             y += ps[i].getY();
102         }
103         x = x / ps.length;
104         y = y / ps.length;
105         Point p = new Point(x, y);
106         Point t = null;
107         for (int i = 0; i < ps.length - 1; i++) {
108             for (int j = 0; j < ps.length - 1 - i; j++) {
109                 if (isAnti(p, ps[j], ps[j + 1])) {
110 
111                     t = ps[j];
112                     ps[j] = ps[j + 1];
113                     ps[j + 1] = t;
114 
115                 }
116 
117             }
118         }
119 
120     }
121 
122     public static boolean isAnti(Point p, Point A, Point B) {
123 /*
124 if (A.getX() >= 0 && B.getX() < 0)
125             return true;
126         if (A.getX() == 0 && B.getX() == 0)
127             return A.getY() > B.getY();
128 
129 
130 */
131         
132         double d = (A.getX() - p.getX()) * (B.getY() - p.getY()) - (B.getX() - p.getX()) * (A.getY() - p.getY());
133         if (d < 0)
134             return true;
135         if (d > 0)
136             return false;
137         double d1 = A.distance(p);
138         double d2 = B.distance(p);
139         return d1 > d2;
140 
141     }
142 
143 
144     public static double area(Point[] ps) {
145 
146         if (ps.length < 3)
147             return 0;
148         int index = 0;
149         Point p1 = ps[index], p2 = ps[index + 1];
150         double result = 0;
151         while (p2 != ps[ps.length - 1]) {
152 
153             result += (p1.getX() * p2.getY()) - (p1.getY() * p2.getX());
154 
155             index++;
156             p1 = ps[index];
157             p2 = ps[index + 1];
158         }
159         result += (p1.getX() * p2.getY()) - (p1.getY() * p2.getX());
160 
161         index++;
162         p1 = ps[index];
163         p2 = ps[0];
164         result += (p1.getX() * p2.getY()) - (p1.getY() * p2.getX());
165         return result / 2;
166 
167     }
168 
169 }

点击查看工具Tool类

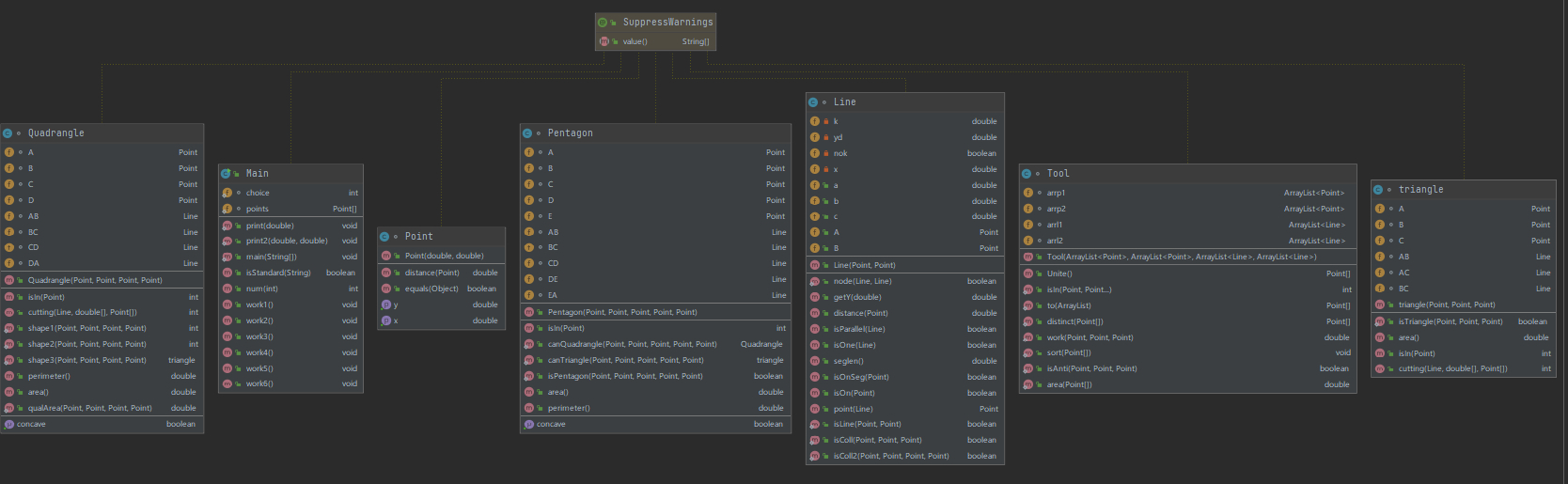
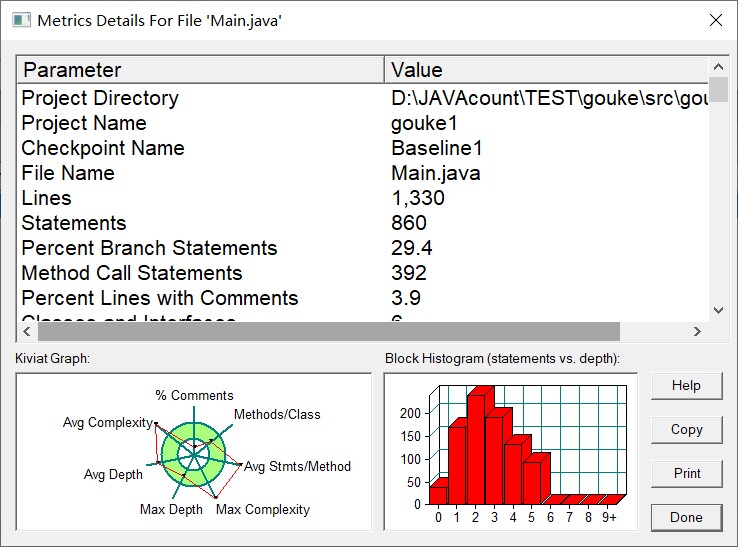
　　选项一判断是否组成五边形，原理还是不能有若干点共线情况以及非邻边不能有交点进行判断即可。

　　选项二判断凹凸性，可以使用每次连续读取三点，直至全部读完，三点构建两个向量，又向量叉乘进行判断：

 1  //是否为凹
 2     public boolean isConcave() {
 3 
 4         double d1 = Tool.work(B, A, C);
 5         double d2 = Tool.work(C, B, D);
 6         double d3 = Tool.work(D, C, E);
 7         double d4 = Tool.work(E, D, A);
 8         double d5 = Tool.work(A, E, B);
 9         if ((d1 > 0 && d2 > 0 && d3 > 0 && d4 > 0 && d5 > 0) || (d1 < 0 && d2 < 0 && d3 < 0 && d4 < 0 && d5 < 0))
10 
11             return false;
12         else
13             return true;
14 }

　　选项三直线切割问题，同样先进行判断五个点围成的图形，三角形就调用三角形切割方法，四边形就调用四边形切割方法，五边形就切割成三角形和四边形两部分分别调用即可

  1  //五边形情况
  2         if (pentagon) {
  3             Pentagon pentagon1 = new Pentagon(points[2], points[3], points[4], points[5], points[6]);
  4             if (line.isOne(pentagon1.AB) || line.isOne(pentagon1.BC) || line.isOne(pentagon1.CD) || line.isOne(pentagon1.DE) || line.isOne(pentagon1.EA)) {
  5                 System.out.println("The line is coincide with one of the lines");
  6                 System.exit(0);
  7             }
  8             if (line.isOne(new Line(pentagon1.A, pentagon1.C))) {
  9                 System.out.print("2 ");
 10                 print2(new triangle(pentagon1.A, pentagon1.B, pentagon1.C).area(), new Quadrangle(pentagon1.A, pentagon1.C, pentagon1.D, pentagon1.E).area());
 11                 System.exit(0);
 12             }
 13             if (line.isOne(new Line(pentagon1.A, pentagon1.D))) {
 14                 System.out.print("2 ");
 15                 print2(new triangle(pentagon1.A, pentagon1.D, pentagon1.E).area(), new Quadrangle(pentagon1.A, pentagon1.B, pentagon1.C, pentagon1.D).area());
 16                 System.exit(0);
 17             }
 18             if (line.isOne(new Line(pentagon1.C, pentagon1.E))) {
 19                 System.out.print("2 ");
 20                 print2(new triangle(pentagon1.C, pentagon1.D, pentagon1.E).area(), new Quadrangle(pentagon1.A, pentagon1.B, pentagon1.C, pentagon1.E).area());
 21                 System.exit(0);
 22             }
 23             triangle triangle1 = new triangle(pentagon1.A, pentagon1.B, pentagon1.C);
 24             Quadrangle quadrangle1 = new Quadrangle(pentagon1.A, pentagon1.C, pentagon1.D, pentagon1.E);
 25             double[] ds1 = new double[2];
 26             double[] ds2 = new double[2];
 27             Point[] ps1 = new Point[2];
 28             Point[] ps2 = new Point[2];
 29             int cutting1 = triangle1.cutting(line, ds1, ps1);
 30             int cutting2 = quadrangle1.cutting(line, ds2, ps2);
 31             if (cutting1 == 0 && cutting2 == 0) {
 32                 System.out.println("0");
 33                 System.exit(0);
 34             }
 35             if (cutting1 == 1 && cutting2 == 0) {
 36                 System.out.println("1");
 37                 System.exit(0);
 38             }
 39             if (cutting2 == 1 && cutting1 == 0) {
 40                 System.out.println("1");
 41                 System.exit(0);
 42             }
 43             if (cutting1 == 1 && cutting2 == 1) {
 44                 System.out.println("1");
 45                 System.exit(0);
 46             }
 47             if (cutting1 == 2) {
 48                 System.out.print("2 ");
 49                 if (cutting2 == 0) {
 50                     double d1 = ds1[0];
 51                     double d2 = ds1[1] + quadrangle1.area();
 52                     print2(d1, d2);
 53                     System.exit(0);
 54                 }
 55                 if (cutting2 == 1) {
 56                     if (ps1[0].equals(pentagon1.B)) {
 57                         double d1 = ds1[0];
 58                         double d2 = ds1[1] + quadrangle1.area();
 59                         print2(d1, d2);
 60                         System.exit(0);
 61                     } else {
 62                         double d1 = ds1[1];
 63                         double d2 = ds1[0] + quadrangle1.area();
 64                         print2(d1, d2);
 65                         System.exit(0);
 66                     }
 67                 }
 68                 if (cutting2 == 2) {
 69                     //133 234
 70                     if (ps1[1] != null && ps2[1] == null) {
 71                         if (ps1[0].equals(ps2[0])) {
 72                             double d1 = ds1[0] + ds2[0];
 73                             double d2 = pentagon1.area() - d1;
 74                             print2(d1, d2);
 75                             System.exit(0);
 76                         } else {
 77                             double d1 = ds1[1] + ds2[0];
 78                             double d2 = pentagon1.area() - d1;
 79                             print2(d1, d2);
 80                             System.exit(0);
 81                         }
 82                     }//133 244
 83                     else if (ps1[1] != null && ps2[1] != null) {
 84                         if (ps2[0].equals(ps1[0]) || ps2[1].equals(ps1[0])) {
 85                             double d1 = ds1[0] + ds2[0];
 86                             double d2 = pentagon1.area() - d1;
 87                             print2(d1, d2);
 88                             System.exit(0);
 89 
 90                         } else {
 91                             double d1 = ds1[1] + ds2[0];
 92                             double d2 = pentagon1.area() - d1;
 93                             print2(d1, d2);
 94                             System.exit(0);
 95                         }
 96 
 97                     }//134 234
 98                     else if (ps1[1] == null && ps2[1] == null) {
 99 
100                         if (ps1[0].equals(ps2[0])) {
101                             double d1 = ds1[0] + ds2[0];
102                             double d2 = pentagon1.area() - d1;
103                             print2(d1, d2);
104                             System.exit(0);
105                         } else {
106                             double d1 = ds1[1] + ds2[0];
107                             double d2 = pentagon1.area() - d1;
108                             print2(d1, d2);
109                             System.exit(0);
110                         }
111 
112                     } else {
113                         if (ps2[0].equals(ps1[0]) || ps2[1].equals(ps1[0])) {
114                             double d1 = ds1[0] + ds2[0];
115                             double d2 = pentagon1.area() - d1;
116                             print2(d1, d2);
117                             System.exit(0);
118 
119                         } else {
120                             double d1 = ds1[1] + ds2[0];
121                             double d2 = pentagon1.area() - d1;
122                             print2(d1, d2);
123                             System.exit(0);
124                         }
125 
126                     }
127 
128 
129                 }
130 
131 
132             }
133             if (cutting2 == 2) {
134                 System.out.print("2 ");
135                 if (cutting1 == 0) {
136                     if (ps2[1] == null) {
137                         double d1 = ds2[0];
138                         double d2 = ds2[1] + triangle1.area();
139                         print2(d1, d2);
140                         System.exit(0);
141                     } else {
142                         if (ps2[0].equals(pentagon1.E) || ps2[1].equals(pentagon1.E)) {
143                             double d1 = ds2[0];
144                             double d2 = ds2[1] + triangle1.area();
145                             print2(d1, d2);
146                             System.exit(0);
147                         } else {
148                             double d1 = ds2[1];
149                             double d2 = ds2[0] + triangle1.area();
150                             print2(d1, d2);
151                             System.exit(0);
152                         }
153                     }
154                 }
155                 if (cutting1 == 1) {
156                     if (ps2[0].equals(pentagon1.E) || ps2[0].equals(pentagon1.D)) {
157                         double d1 = ds2[0];
158                         double d2 = ds2[1] + triangle1.area();
159                         print2(d1, d2);
160                         System.exit(0);
161                     } else {
162                         double d1 = ds2[1];
163                         double d2 = ds2[0] + triangle1.area();
164                         print2(d1, d2);
165                         System.exit(0);
166                     }
167                 }
168 
169 
170             }
171 
172 
173         }

　　选项四五六推荐倒着做，因为六五四是又简到繁，且会用到之前的：

　　选项六较为简单，可以统一根据面积法进行判断，所求点和多边形每条边组成若干个三角形，每个面积和相加与多边形面积是否相同来进行判断

 1  public int isIn(Point p) {
 2 
 3         if (AB.isOnSeg(p) || BC.isOnSeg(p) || CD.isOnSeg(p) || DA.isOnSeg(p)) {
 4             return -1;
 5         }
 6         if (new Line(B, D).isOnSeg(p))
 7             return 1;
 8         if (new triangle(A, B, D).isIn(p) == 1 || new triangle(B, C, D).isIn(p) == 1)
 9             return 1;
10         return 0;
11     }

　　选项五将前五个点组成的多边形的每个点放到一个集合里面，每条边放到另一个集合里面，后五个点执行同样的操作，然后求两个边集合所有边的相交情况，如果有交点且在两条线段之内，就保存到unite集合里面，然后遍历两个点集合，如果该点同时存在两个多边形之内，也保存到unite集合里面，然后对unite集合进行去重、顺逆时针排序，利用鞋带定理求得面积即可：

 1 public void work5() {
 2 
 3         ArrayList<Point> p1 = new ArrayList<>();
 4         ArrayList<Point> p2 = new ArrayList<>();
 5         ArrayList<Line> l1 = new ArrayList<>();
 6         ArrayList<Line> l2 = new ArrayList<>();
 7         boolean b1 = Pentagon.isPentagon(points[0], points[1], points[2], points[3], points[4]);
 8         boolean b2 = Pentagon.isPentagon(points[5], points[6], points[7], points[8], points[9]);
 9         triangle t1 = Pentagon.canTriangle(points[0], points[1], points[2], points[3], points[4]);
10         triangle t2 = Pentagon.canTriangle(points[5], points[6], points[7], points[8], points[9]);
11         Quadrangle q1 = Pentagon.canQuadrangle(points[0], points[1], points[2], points[3], points[4]);
12         Quadrangle q2 = Pentagon.canQuadrangle(points[5], points[6], points[7], points[8], points[9]);
13         if (b1) {
14             Pentagon pentagon1 = new Pentagon(points[0], points[1], points[2], points[3], points[4]);
15             p1.add(pentagon1.A);
16             p1.add(pentagon1.B);
17             p1.add(pentagon1.C);
18             p1.add(pentagon1.D);
19             p1.add(pentagon1.E);
20             l1.add(pentagon1.AB);
21             l1.add(pentagon1.BC);
22             l1.add(pentagon1.CD);
23             l1.add(pentagon1.DE);
24             l1.add(pentagon1.EA);
25         } else if (t1 != null) {
26             p1.add(t1.A);
27             p1.add(t1.B);
28             p1.add(t1.C);
29             l1.add(t1.AB);
30             l1.add(t1.BC);
31             l1.add(t1.AC);
32         } else if (q1 != null) {
33             p1.add(q1.A);
34             p1.add(q1.B);
35             p1.add(q1.C);
36             p1.add(q1.D);
37             l1.add(q1.AB);
38             l1.add(q1.BC);
39             l1.add(q1.CD);
40             l1.add(q1.DA);
41 
42         }
43         if (b2) {
44             Pentagon pentagon2 = new Pentagon(points[5], points[6], points[7], points[8], points[9]);
45             p2.add(pentagon2.A);
46             p2.add(pentagon2.B);
47             p2.add(pentagon2.C);
48             p2.add(pentagon2.D);
49             p2.add(pentagon2.E);
50             l2.add(pentagon2.AB);
51             l2.add(pentagon2.BC);
52             l2.add(pentagon2.CD);
53             l2.add(pentagon2.DE);
54             l2.add(pentagon2.EA);
55         } else if (t2 != null) {
56             p2.add(t2.A);
57             p2.add(t2.B);
58             p2.add(t2.C);
59             l2.add(t2.AB);
60             l2.add(t2.BC);
61             l2.add(t2.AC);
62         } else if (q2 != null) {
63             p2.add(q2.A);
64             p2.add(q2.B);
65             p2.add(q2.C);
66             p2.add(q2.D);
67             l2.add(q2.AB);
68             l2.add(q2.BC);
69             l2.add(q2.CD);
70             l2.add(q2.DA);
71         }
72         Tool tool = new Tool(p1, p2, l1, l2);
73         Point[] unite = tool.Unite();
74         unite = Tool.distinct(unite);
75         Tool.sort(unite);
76         double area = Tool.area(unite);
77         print(area);
78 
79     }

点击查看代码

　　选项四可以直接用选项五里面经过去重排序之后的unite集合来判断：

如果集合大小为0，就是“分离”；

集合大小为1或者2，就是“连接”；

集合所有点和多边形1和多边形2的点重复，就是“完全重合”；

跟一个多边形的点重复而另一个不等，就是“包含”/“被包含”;

全部都不是就是“交错”；

同时还要记录多边形1和多边形2的形状，输出时要用到：

  1  public void work4() {
  2         ArrayList<Point> p1 = new ArrayList<>();
  3         ArrayList<Point> p2 = new ArrayList<>();
  4         ArrayList<Line> l1 = new ArrayList<>();
  5         ArrayList<Line> l2 = new ArrayList<>();
  6         boolean b1 = Pentagon.isPentagon(points[0], points[1], points[2], points[3], points[4]);
  7         boolean b2 = Pentagon.isPentagon(points[5], points[6], points[7], points[8], points[9]);
  8         triangle t1 = Pentagon.canTriangle(points[0], points[1], points[2], points[3], points[4]);
  9         triangle t2 = Pentagon.canTriangle(points[5], points[6], points[7], points[8], points[9]);
 10         Quadrangle q1 = Pentagon.canQuadrangle(points[0], points[1], points[2], points[3], points[4]);
 11         Quadrangle q2 = Pentagon.canQuadrangle(points[5], points[6], points[7], points[8], points[9]);
 12         String[] str = {"triangle", "quadrilateral", "pentagon"};
 13         int i1 = 0, i2 = 0;
 14         if (b1) {
 15             Pentagon pentagon1 = new Pentagon(points[0], points[1], points[2], points[3], points[4]);
 16             p1.add(pentagon1.A);
 17             p1.add(pentagon1.B);
 18             p1.add(pentagon1.C);
 19             p1.add(pentagon1.D);
 20             p1.add(pentagon1.E);
 21             l1.add(pentagon1.AB);
 22             l1.add(pentagon1.BC);
 23             l1.add(pentagon1.CD);
 24             l1.add(pentagon1.DE);
 25             l1.add(pentagon1.EA);
 26             i1 = 2;
 27         } else if (t1 != null) {
 28             p1.add(t1.A);
 29             p1.add(t1.B);
 30             p1.add(t1.C);
 31             l1.add(t1.AB);
 32             l1.add(t1.BC);
 33             l1.add(t1.AC);
 34             i1 = 0;
 35         } else if (q1 != null) {
 36             p1.add(q1.A);
 37             p1.add(q1.B);
 38             p1.add(q1.C);
 39             p1.add(q1.D);
 40             l1.add(q1.AB);
 41             l1.add(q1.BC);
 42             l1.add(q1.CD);
 43             l1.add(q1.DA);
 44             i1 = 1;
 45         }
 46         if (b2) {
 47             Pentagon pentagon2 = new Pentagon(points[5], points[6], points[7], points[8], points[9]);
 48             p2.add(pentagon2.A);
 49             p2.add(pentagon2.B);
 50             p2.add(pentagon2.C);
 51             p2.add(pentagon2.D);
 52             p2.add(pentagon2.E);
 53             l2.add(pentagon2.AB);
 54             l2.add(pentagon2.BC);
 55             l2.add(pentagon2.CD);
 56             l2.add(pentagon2.DE);
 57             l2.add(pentagon2.EA);
 58             i2 = 2;
 59         } else if (t2 != null) {
 60             p2.add(t2.A);
 61             p2.add(t2.B);
 62             p2.add(t2.C);
 63             l2.add(t2.AB);
 64             l2.add(t2.BC);
 65             l2.add(t2.AC);
 66             i2 = 0;
 67         } else if (q2 != null) {
 68             p2.add(q2.A);
 69             p2.add(q2.B);
 70             p2.add(q2.C);
 71             p2.add(q2.D);
 72             l2.add(q2.AB);
 73             l2.add(q2.BC);
 74             l2.add(q2.CD);
 75             l2.add(q2.DA);
 76             i2 = 1;
 77         }
 78         Tool tool = new Tool(p1, p2, l1, l2);
 79         Point[] unite = tool.Unite();
 80         unite = Tool.distinct(unite);
 81         if (unite == null) {
 82 
 83             System.out.println("no overlapping area between the previous "+str[i1]+" and the following "+str[i2]);
 84             System.exit(0);
 85         }
 86         if(unite.length == 1||unite.length == 2){
 87 
 88             System.out.println("the previous "+str[i1]+" is connected to the following "+str[i2]);
 89             System.exit(0);
 90         }
 91         boolean f1 = true,f2 = true;
 92         ArrayList<Point> arrayList = new ArrayList<>();
 93         for (int i = 0; i < unite.length; i++) {
 94             arrayList.add(unite[i]);
 95         }
 96         for (int i = 0; i < p1.size(); i++) {
 97             if(Tool.isIn(p1.get(i),Tool.to(arrayList))==0)
 98                 f1 = false;
 99         }
100         for (int i = 0; i < p2.size(); i++) {
101             if(Tool.isIn(p2.get(i),Tool.to(arrayList))==0)
102                 f2 = false;
103         }
104 
105     //    System.out.println("the previous "+str[1]+" coincides with the following "+str[1]);
106 
107         if(f1&&f2){
108 
109             System.out.println("the previous "+str[i1]+" coincides with the following "+str[i2]);
110             System.exit(0);
111         }
112         if(f1&&(!f2)){
113 
114             System.out.println("the previous "+str[i1]+" is inside the following "+str[i2]);
115             System.exit(0);
116         }
117 
118         if(f2&&(!f1)){
119 
120             System.out.println("the previous "+str[i1]+" contains the following "+str[i2]);
121             System.exit(0);
122         }
123 
124 
125 
126             System.out.println("the previous "+str[i1]+" is interlaced with the following "+str[i2]);
127             System.exit(0);
128 
129 
130 
131 
132     }

点击查看代码

　　期中考试7-1点与线（类设计）：

设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format


设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息，输出格式如下：

  ```
      The line's color is:颜色值
      The line's begin point's Coordinate is:
      (x1,y1)
      The line's end point's Coordinate is:
      (x2,y2)
      The line's length is:长度值
  ```

其中，所有数值均保留两位小数，建议可用String.format("%.2f", data)方法。



输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色，中间可用一个或多个空格、tab或者回车分隔。
输出格式:
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值

点击查看题目

本题只需要按照题目的意思一步步走即可，依题意设计Point类和Line类：

 1 class Point {
 2 
 3     private double x;
 4     private double y;
 5 
 6     public Point(double x, double y) {
 7         this.x = x;
 8         this.y = y;
 9     }
10 
11     public double distance(Point point) {
12 
13         return Math.sqrt((x - point.x) * (x - point.x) + (y - point.y) * (y - point.y));
14     }
15 
16     public double getX() {
17         return x;
18     }
19 
20     public void setX(double x) {
21         this.x = x;
22     }
23 
24     public double getY() {
25         return y;
26     }
27 
28     public void setY(double y) {
29         this.y = y;
30     }
31 
32     public void display() {
33         System.out.println(this);
34     }
35 
36     @Override
37     public String toString() {
38         return "(" + Main.t(this.x) + "," + Main.t(this.y) + ")";
39     }
40 }
41 
42 
43 class Line {
44 
45     private Point A;
46     private Point B;
47     private String color;
48 
49     public Line(Point a, Point b, String color) {
50         A = a;
51         B = b;
52         this.color = color;
53     }
54 
55     public double getDistance() {
56         return A.distance(B);
57     }
58 
59     public void display() {
60 
61         System.out.println("The line's color is:" + this.color);
62         System.out.println("The line's begin point's Coordinate is:");
63         System.out.println(this.A);
64         System.out.println("The line's end point's Coordinate is:");
65         System.out.println(this.B);
66         System.out.print("The line's length is:");
67         Main.print(this.getDistance());
68     }
69 
70     public Point getA() {
71         return A;
72     }
73 
74     public void setA(Point a) {
75         A = a;
76     }
77 
78     public Point getB() {
79         return B;
80     }
81 
82     public void setB(Point b) {
83         B = b;
84     }
85 
86     public String getColor() {
87         return color;
88     }
89 
90     public void setColor(String color) {
91         this.color = color;
92     }
93 }

点击查看Point和Line类

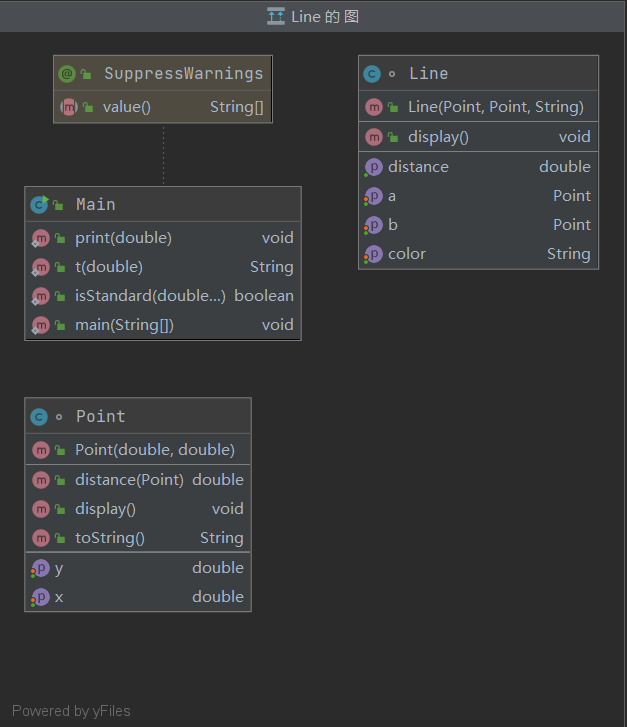
主程序里只需要进行读取数据，并判断数据是否，然后构建Line对象调用display方法即可。我使用isStandard方法（可变参数）来判断传进去的各个数据是否有不合理的数据：

1 public static boolean isStandard(double... doubles) {
2 
3         for (int i = 0; i < doubles.length; i++) {
4             if (doubles[i] <= 0 || doubles[i] > 200)
5                 return false;
6         }
7         return true;
8     }

 1   public static void main(String[] args) {
 2 
 3         double x1 = 0, y1 = 0, x2 = 0, y2 = 0;
 4         String str = "";
 5         Scanner scanner = new Scanner(System.in);
 6         x1 = scanner.nextDouble();
 7         y1 = scanner.nextDouble();
 8         x2 = scanner.nextDouble();
 9         y2 = scanner.nextDouble();
10         str = scanner.next();
11         if (!isStandard(x1, y1, x2, y2)) {
12             System.out.println("Wrong Format");
13             System.exit(0);
14         }
15         Line line = new Line(new Point(x1, y1), new Point(x2, y2), str);
16         line.display();
17 
18 
19     }

　　期中考试7-2 点线面问题重构（继承与多态）

在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。
对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性。示例代码如下：
      element = p1;//起点Point
      element.display();
      
      element = p2;//终点Point
      element.display();
      
      element = line;//线段
      element.display();
      
      element = plane;//面
      element.display();

输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色，中间可用一个或多个空格、tab或者回车分隔。
输出格式:
(x1,y1)
(x2,y2)
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
The Plane's color is:颜色值

点击查看题目

同样，依题意设计Element抽象类，并设计Plane类，和之前的点线类都继承Element类：

1 abstract class Element {
2     abstract void display();
3 }

主程序进行读取数据、构建对象、调用display方法即可：

 1  public static void main(String[] args) {
 2 
 3         double x1 = 0, y1 = 0, x2 = 0, y2 = 0;
 4         String str = "";
 5         Scanner scanner = new Scanner(System.in);
 6         x1 = scanner.nextDouble();
 7         y1 = scanner.nextDouble();
 8         x2 = scanner.nextDouble();
 9         y2 = scanner.nextDouble();
10         str = scanner.next();
11         if (!isStandard(x1, y1, x2, y2)) {
12             System.out.println("Wrong Format");
13             System.exit(0);
14         }
15         Point p1 = new Point(x1, y1);
16         Point p2 = new Point(x2, y2);
17         Plane plane = new Plane(str);
18         Line line = new Line(p1, p2, str);
19         Element element = null;
20         element = p1;//起点Point
21         element.display();
22 
23         element = p2;//终点Point
24         element.display();
25 
26         element = line;//线段
27         element.display();
28 
29         element = plane;//面
30         element.display();
31 
32 
33 
34 }

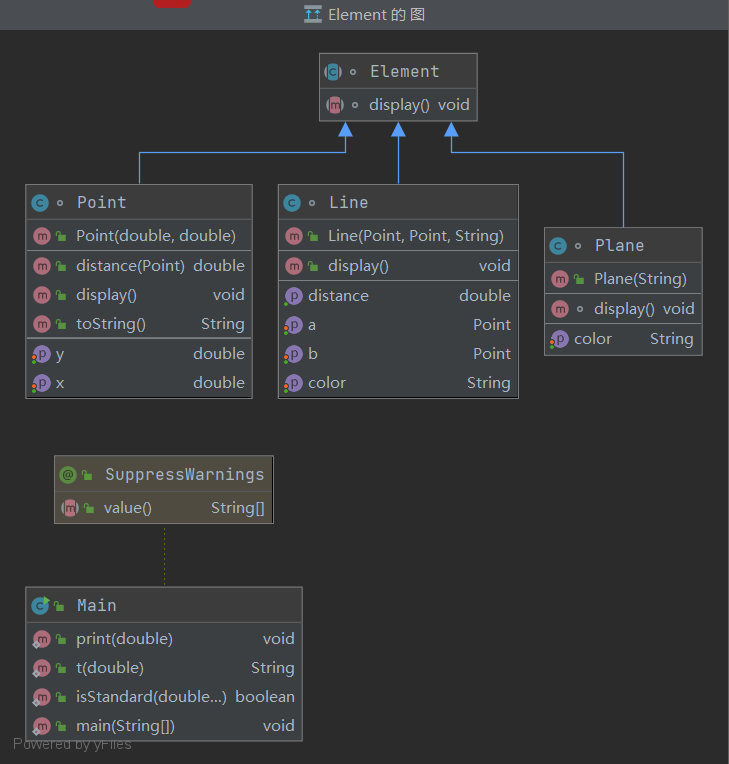
　　7-3 点线面问题再重构（容器类）

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。
在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象
在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：
1：向容器中增加Point对象
2：向容器中增加Line对象
3：向容器中增加Plane对象
4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
0：输入结束
输入格式:
switch(choice) {
            case 1://insert Point object into list 
              输入“点”对象的x，y值
                break;
            case 2://insert Line object into list
                输入“线”对象两个端点的x，y值
                break;
            case 3://insert Plane object into list
                输入“面”对象的颜色值
                break;
            case 4://delete index - 1 object from list
                输入要删除的对象位置（从1开始）
                ...
            }
输出格式:
Point、Line、Plane的输出参考题目2
删除对象时，若输入的index超出合法范围，程序自动忽略该操作

点击查看题目

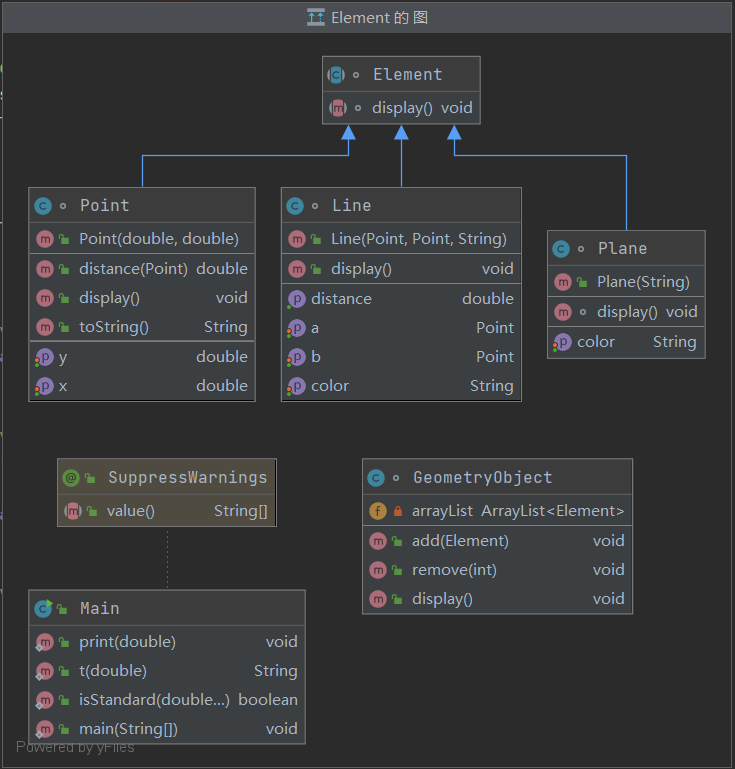
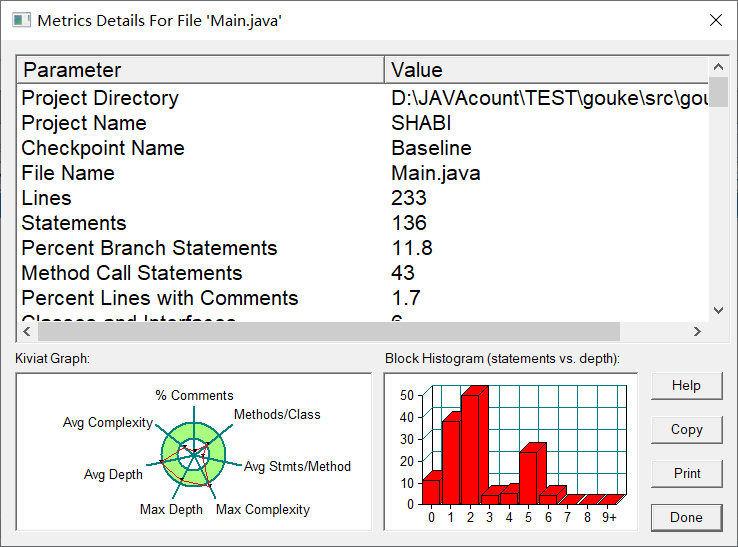
　　在第二题的基础上再设计GeometryObject类，同样参照题目的提示即可，主程序进行读取数据、构建对象、调用display方法即可：

 1 class GeometryObject {
 2 
 3     private ArrayList<Element> arrayList = new ArrayList<>();
 4 
 5     public void add(Element element) {
 6         arrayList.add(element);
 7     }
 8 
 9    public void remove(int index) {
10         if (index<=0||index>arrayList.size())
11             return;
12         arrayList.remove(index - 1);
13     }
14 
15     public void display(){
16         for (Element element : arrayList) {
17             element.display();
18         }
19 
20     }
21 
22 }

 1  public static void main(String[] args) {
 2 
 3 
 4         double x1 = 0, y1 = 0, x2 = 0, y2 = 0;
 5         String str = "";
 6         Scanner scanner = new Scanner(System.in);
 7         GeometryObject geometryObject = new GeometryObject();
 8 
 9 
10         Point p1 = null, p2 = null;
11         Plane plane = null;
12         Line line = null;
13 
14         int choice = scanner.nextInt();
15         while (choice != 0) {
16             switch (choice) {
17                 case 1://insert Point object into list
18                     x1 = scanner.nextDouble();
19                     y1 = scanner.nextDouble();
20                     if (!isStandard(x1, y1)) {
21                         System.out.println("Wrong Format");
22                         System.exit(0);
23                     }
24                     p1 = new Point(x1, y1);
25                     geometryObject.add(p1);
26                     break;
27                 case 2://insert Line object into list
28                     x1 = scanner.nextDouble();
29                     y1 = scanner.nextDouble();
30                     x2 = scanner.nextDouble();
31                     y2 = scanner.nextDouble();
32                     if (!isStandard(x1, y1, x2, y2)) {
33                         System.out.println("Wrong Format");
34                         System.exit(0);
35                     }
36                     str = scanner.next();
37                     p1 = new Point(x1, y1);
38                     p2 = new Point(x2, y2);
39                     line = new Line(p1, p2, str);
40                     geometryObject.add(line);
41                     break;
42                 case 3://insert Plane object into list
43                     str = scanner.next();
44                     plane = new Plane(str);
45                     geometryObject.add(plane);
46                     break;
47                 case 4://delete index - 1 object from list
48                     int index = scanner.nextInt();
49                     geometryObject.remove(index);
50 
51             }
52             choice = scanner.nextInt();
53         }
54 
55         geometryObject.display();
56 
57 
58 }

点击查看主方法

三、踩坑心得

- 1.作业四：7-2前三个选项的输出有优先级，当不能组成四边形时输出“not a quadrilateral”，有重复点输出“points coincide”，可有重复点不然无法组成四边形，经测试应该输出“not a quadrilateral”而不是另一个，这一点很坑。还有选项四考虑四个点可以组成四边形的情况时，题目的描述很难理解，而且应该先进行去重，我自己在做的时候就没太读懂，没有先进行去重导致错误。
- 2.作业五：“多边形系列”题阴间的地方在于测试点很多很多，本题五边形可以说达到了顶点，而且还要调用之前的点、线、三角形、四边形类，非常考验对之前类的设计，可以说容易出错的地方极多极多，比如少考虑了什么特殊情况，又或者是之前的四个类有什么没有发现的bug（这种情况是最难发现的，因为你一遍都会在本次的设计中去找寻错误，而很少去想之前的是不是出了问题），可以说及其考验设计能力、耐心、细心度、找寻错误的能力，可能踩的小坑数不胜数，每个人遇到的情况也不完全一样……总之，在遇到这类“大型”题目的时候，一定要静下心来，找寻各个需求的共同点，多去包装类，每个类都要进行多次验证确保无误，一个一个选项攻破，切不可心急！！！
- 3.期中考试：考试内容较为简单，基本没什么坑，很直白都，只要理解了多态的使用，就可以很顺利的做出来

四、改进建议

　　作业四和作业五作为“多边形”系列最复杂的两道题，会调用到很多之前包装过的类的方法，而之前在设计类的时候，可能没想过后续还会用到，从而设计的不符合逻辑，很难后续调　　用，可以对之前的Point、Line、triangle类进行重构，把无用的方法舍去，把有效的方法进一步重构的更合理，更统一，才能在调用方法的时候不至于在这些基本方面而犯迷糊，而把工作重心放在如何解决问题本身上。

五、心得体会

1.如果有需要设计多个类来解决问题的时候，一定要对每一个类多次测试验证，把错误率降到最低，循序渐进，这样也能尽量避免盲目找寻bug的情况。

　　2.要做到深刻理解面向对象的思想，永远都要先想着工作由谁来做，而不是怎么去做，这样设计出的程序结构会更加明朗。

3.通过这几次的PTA大作业，最大的感受就是个人的能力是有限的，有时候自己实在找不到自己漏掉了什么情况，一定要找同学帮忙，同时学习别人的算法思路，看看是否比自己的简便。

posted @ 2022-10-29 11:00 WK666 阅读(60) 评论(0) 收藏举报

刷新页面返回顶部

kmld

OO第二次博客作业

OO第二次博客作业（PTA第四次、第五次作业及期中考试）

目录

一、作业总结

二、设计与分析

作业五：点线形系列5-凸五边形的计算

三、踩坑心得

四、改进建议

五、心得体会

公告