二分法边界思考(续)

二分法边界思考(续)

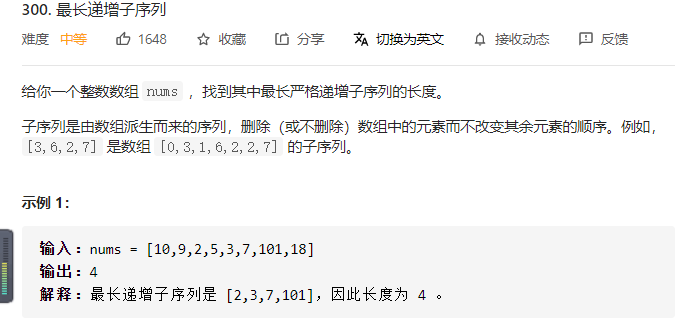
本题思路是使相同长度下序列增长要尽可能慢

package leetCode.动态规划;

/**
 * @author km
 * @date 2021年06月11日
 **/
public class LongestIncreasingSubsequence {
    public static void main(String[] args) {
        LongestIncreasingSubsequence main = new LongestIncreasingSubsequence();
        System.out.println(main.lengthOfLIS(new int[]{4,10,4,3,8,9}));
    }
    public int lengthOfLIS(int[] nums) {
        int length = nums.length;
        int[] tail = new int[length + 1];
        tail[1] = nums[0];
        int len = 1;
        for (int i = 1; i < length; i++) {
            if (nums[i] > tail[len]) {
                tail[++len] = nums[i];
            } else {
                int left = 1, right = len, pos = 0;
                while (left <= right) {
                    int mid = left + ((right - left) >> 1);
                    if (tail[mid] >= nums[i]) {
                        right = mid - 1;
                        pos = right;
                    } else {
                        left = mid + 1;
                    }
                }
                tail[pos + 1] = nums[i];
            }
        }
        return len;
    }
}

在使用二分法的时候，最后需要返回的位置应该如何思考？

• 需要确定目标位置，是最后一个不小于的位置，大于的位置，这关系到if判断时需不需要用等号
  • 在本题中需要确定的是不大于的下界位置，需要在if判断时用等号
• 确定需要替换的位置
  • 例如在本题中最后区间的位置应该是，逻辑位置的下沿间隙中(可以借鉴间隙锁)，想象成小数，0.5是处在0与1的间隙
  • 需要替换的是下沿的后面第一个位置，所以+1