动态规划梳理笔记（一）

动态规划梳理笔记（一）

解决的问题

• 计数
  • 有多少种方法走到右下角
  • 有多少种从k个数中选出和为sum的选法
• 求取最大最小值
  • 左上角至右下角路径的最大和
  • 最长上升子序列的长度
• 求存在性
  • 能不能选出k个数使得和是sum

确定状态

• 最后一步：最优策略中的最后一步决策
• 子问题：最优策略除去最后一步子问题与原问题相比规模更小

初始条件与边界条件

• 需要设置由转移状态方程不可正确设置的初始状态

实例

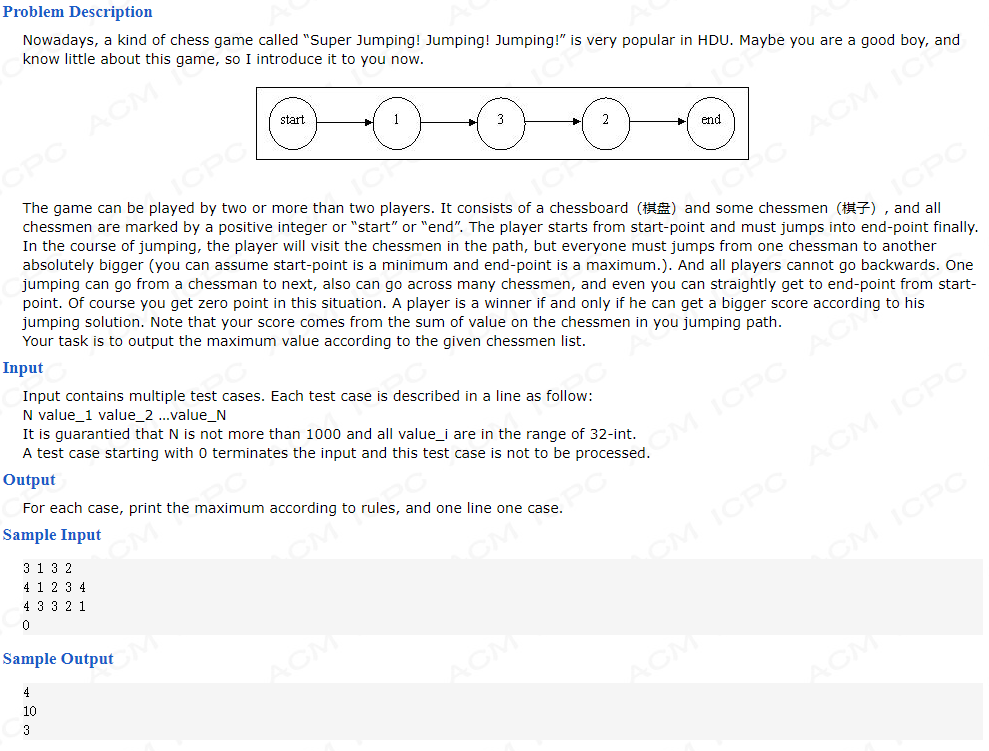
• 一个典型的动态规划问题，求取最大的上升序列的和，于此类似的是求取最大上升子序列的长度

• 考虑最后一步，在列表中到达序号为i的最后一个数字，其能够组成的最大长度应该是，前序列表中所有比新加入数字小的数字中最大和，与本数字的组和。

• 子问题是：到达序列i-1的所能有的最大和

• 核心代码：

  int[] dp = Arrays.copyOf(list, list.length);
  int max = dp[0];
  for (int i = 0; i < list.length; i++) {
      for (int j = 0; j < i; j++) {
          if (list[i] > list[j]) {
              dp[i] = Math.max(dp[i], dp[j] + list[i]);
              if (dp[i] > max){
                  max = dp[i];
              }
          }
      }
  }
  

实例

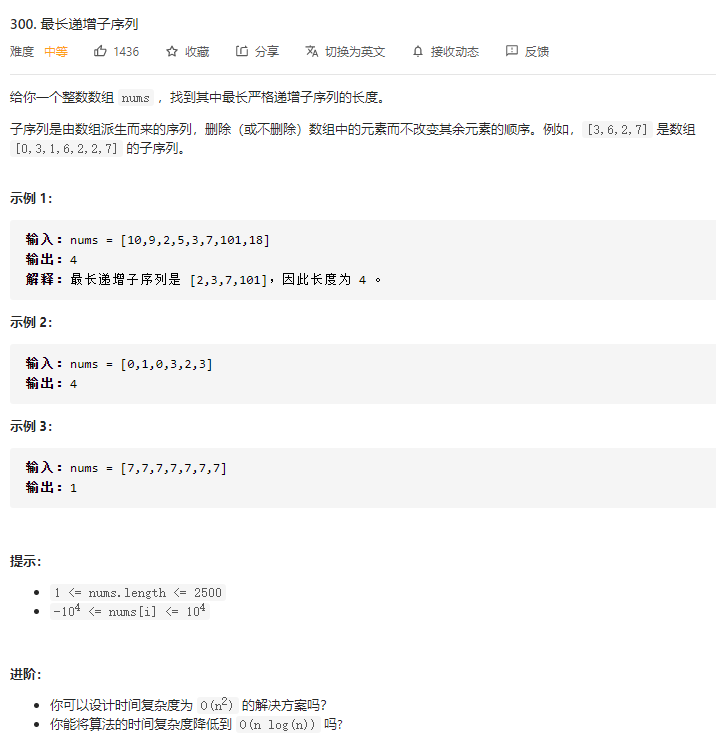
• 求取最长上升子序列的长度时动态规划的经典问题

• 最后一步所加入的数字是前序所有较小数字中长度最大值+ 1

• 可以发现动态规划问题最后一步的一个经典方法是dp[i]中i代表索引，通过索引的增加直至数据全部遍历完成既可以得到最优解

• 优化：

  • 我们关注的是上升序列尾值的情况，同一长度尾部值越小，其越有可能构成最长上升子序列
  • 如果将dp[i- 1]指示为长度为i - 1的上升子序列的尾部值，在当前值大于尾部值时更新dp[i]为当前值，在当前值小于尾部值时，更新1~i- 1中相应位置的尾部，最后根据数字长度获取最大上升子序列的长度。

• 核心代码：

  int len = 1;
  for (int i = 1; i < nums.length; i++) {
      if (nums[i] > tail[len]) {
          tail[++len] = nums[i];
      } else {
          int l = 1, r = len, pos = 0; //通过二分查找获取相应位置
          while (l <= r) {
              int mid = (l + r) >> 1;
              if (tail[mid] < nums[i]) {
                  l = mid + 1;
                  pos = mid; //获得第一个大于nums[i]数字的左沿
              } else {
                  r = mid - 1;
              }
          }
          tail[pos + 1] = nums[i];
      }
  }
  return len;
  

新的情况

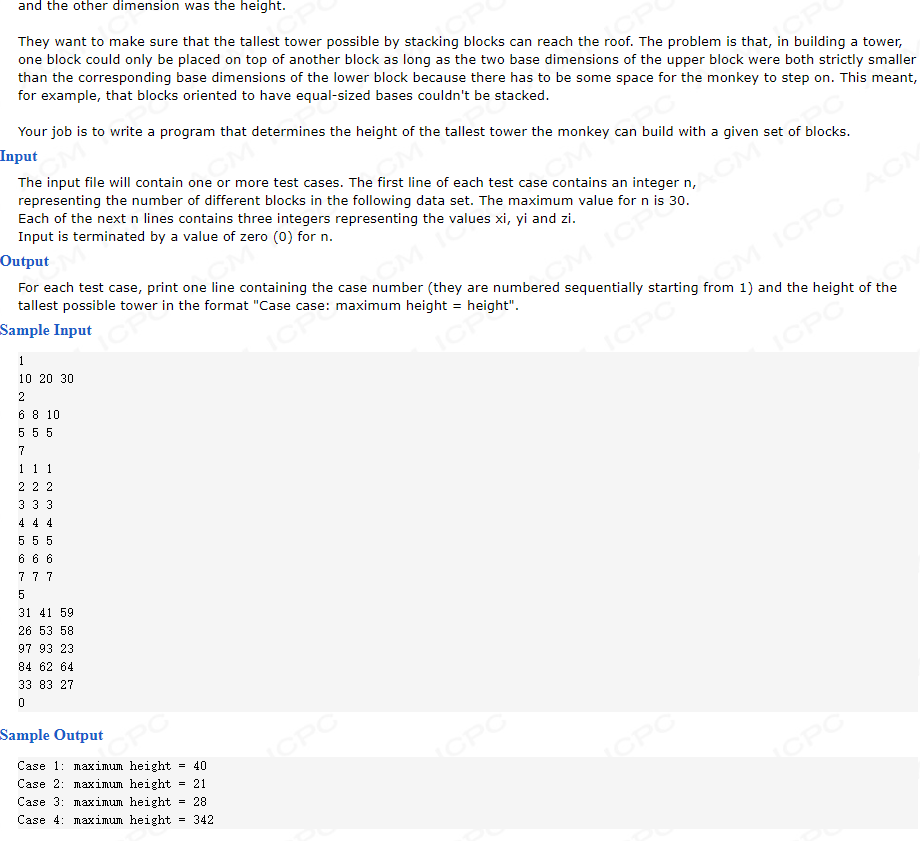
• 在本问题中需要获得塔的最大高度，只有长和宽均满足绝对增长才能符合条件，其与上一题类似，都是求取最长上升序列的最大路径和，不同的是本题要求两组数字均为绝对向上增长，如何解决？

• 如果我们能过够确定一个变量，那么只需要检测另外一个变量最大上升递增就行的高和就可以获得答案，解决办法是按照长升序排序，这样我们只需关注宽的递增就行，问题是长可能相等，导致在检测宽时有不必要的元素选取。解决思路是将同长时的宽按照降序排列，这样同长时必定只选取了一种宽的情况。

• 核心代码：

  static class rectangle implements Comparable<rectangle>{
      int x,y,height;
      rectangle(int x,int y,int height){
          this.x=x;
          this.y=y;
          this.height=height;
      }
      @Override
      public int compareTo(rectangle r) {
          if(this.x>r.x)
              return 1;
          else if(this.x<r.x)
              return -1;
          else
              return this.y-r.y;
      }
  }
  Collections.sort(arr);
  int a[]=new int[6*n];
  for(int i=0;i<6*n;i++){
      a[i]=arr.get(i).height;
  }
  int sum=a[0];
  for(int i=0;i<arr.size();i++){
      int tmp=arr.get(i).height;
      for(int j=0;j<i;j++){
          if(arr.get(i).x>arr.get(j).x&&arr.get(i).y>arr.get(j).y){
              a[i]=Math.max(a[i], a[j]+tmp);
          }
      }
      if(sum<a[i]){
          sum=a[i];
      }
  }
  

实例

• 本题需要求取最长的公共子串，如何解决？

• 若用dp[i] [j]指示两字符串索引位置分别为i j时的最长公共子序列长度，推断下一个状态，若相同，则是上一个状态 + 1,若不同，取值在之前状态种寻找。

• 核心代码：

  int[][] dp = new int[1005][1005];
  for (int i = 1; i <= len1; i++) {
      for (int j = 1; j <= len2; j++) {
          if (s1[i - 1] == s2[j - 1])
              dp[i][j] = dp[i - 1][j - 1] + 1;
          else if (dp[i-1][j] >= dp[i][j-1])
              dp[i][j] = dp[i-1][j];
          else
              dp[i][j] = dp[i][j-1];
      }
  }
  

实例

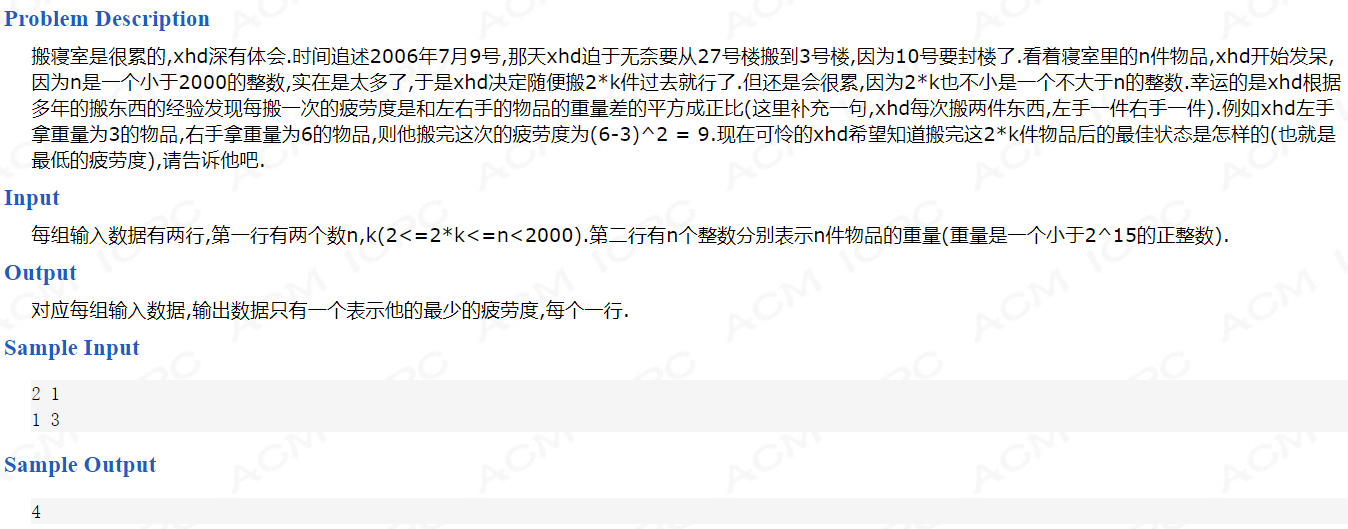
• 一个猜想，动态规划问题的一个解决思路，根据加入数据来进行演绎，在上一题中，通过变化i，j索引来控制数据的加入，推进得到最终结果。

• 显然最小疲劳度是在物品重量升序时产生的，在本题中抉择第i个物品时，有两个选择，选择i,则结果是dp[i - 1] + i与i-1的疲劳度，不选择i则继承dp[i]的疲劳度

• 核心代码：

  for (int i = 2; i <= len - 1; i++) {
      for (int j = 1; 2 * j <= i && j <= k; j++) {
          dp[i][j] = Math.min(dp[i - 1][j], dp[i - 2][j - 1] + (int) Math.pow((goods[i]-goods[i - 1]),2));
      }
  }
  

• 一点想法：动态规划就是一种遍历，不同之处在于会将各层次的结果进行存储，在尝试进行动态规划的时候需要演绎限制条件与变化，寻找各层次变化之间的关系也就是状态转移方程。