背包问题总结

背包问题总结

01背包问题

• 01背包问题解决一个这样的问题，即在付出的代价有限，选取的物品也有限的条件(拿与不拿）下如何达到最优解的问题。
• 面临的棘手情况是，并不是代价可以承受的情况下总是选择拿取物品，所获得的价值会达到最大，可能出现由于首先拿取一个低价值的物品导致无法后续高价值的物品无法拿取错失最优价值的情况。

解决办法：

• 如果我们遍历所有可能，通过比较那么我们一定可以得到最优解，但是代价过于高昂，存在许多子问题的冗余计算的过程，若要解决子问题的冗余，能否将子问题的状态保存，之后再在需要时找出，这样就能避免大量的计算。

• 动态规划将大问题分解为一个个子问题，父问题的最优解有赖于子问题最优解的来实现，譬如：如果我们拥有 i- 1种物品在0_{n**种代价限制的情况下的最优解，我们能否找出**i**种物品**0}n情况的最优解呢？

• 在是否选择第i件物品的当口，我们有两种选择：

  • 不选择：直接继承i-1在代价限制条件下的最优解

  • 选择：那么在付出代价之后我们可以将付出代价后的最优解与i物品的价值组合获得最优解

  • 目标是获得选择/不选择情况下的最优解，所以可以选择其中的最大值

  • 代码实现：

    if(j<space[i])
        dp[i][j]=dp[i-1][j];
    else 
        dp[i][j]=max(dp[i-1][j],dp[i-1][j-space[i]]+val[i]);
    

• 空间优化：

  • 如用一个一维数组记录，通过逆序遍历，通过比较dp[i]与dp[i - w] + v(倒序情况下dp[i-w]没有被更新)既可以获得最优解

  • 代码实现：

    for(i=1;i<=N;i++)//遍历n种物品选择情况
    {
        for(j=C;j>=space[i];j--)//倒序同时保证代价能够承受
        {
            dp[j]=max(dp[j],dp[j-space[i]]+val[i]);
        }
    }
    

实际问题分析

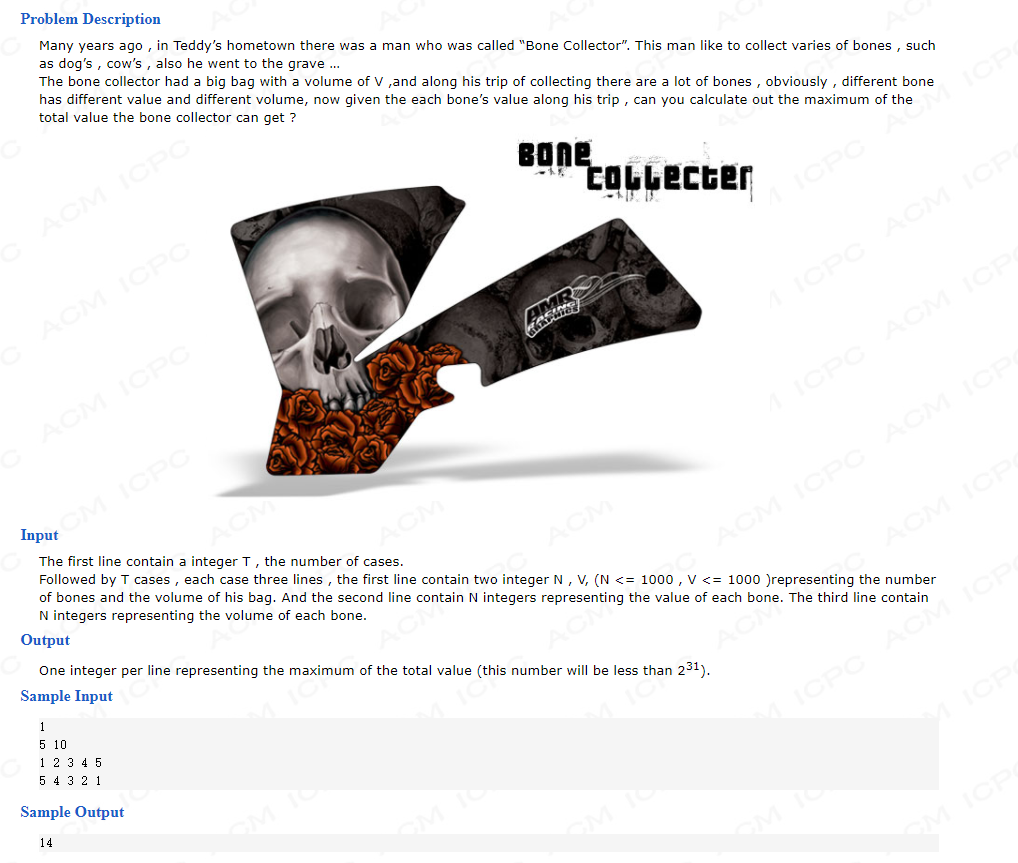
• 这是一个典型的01背包问题，在背包体积有限为V的情况下有N件物品进行选择，每件物品都有相应的价值与代价

一个有趣的问题

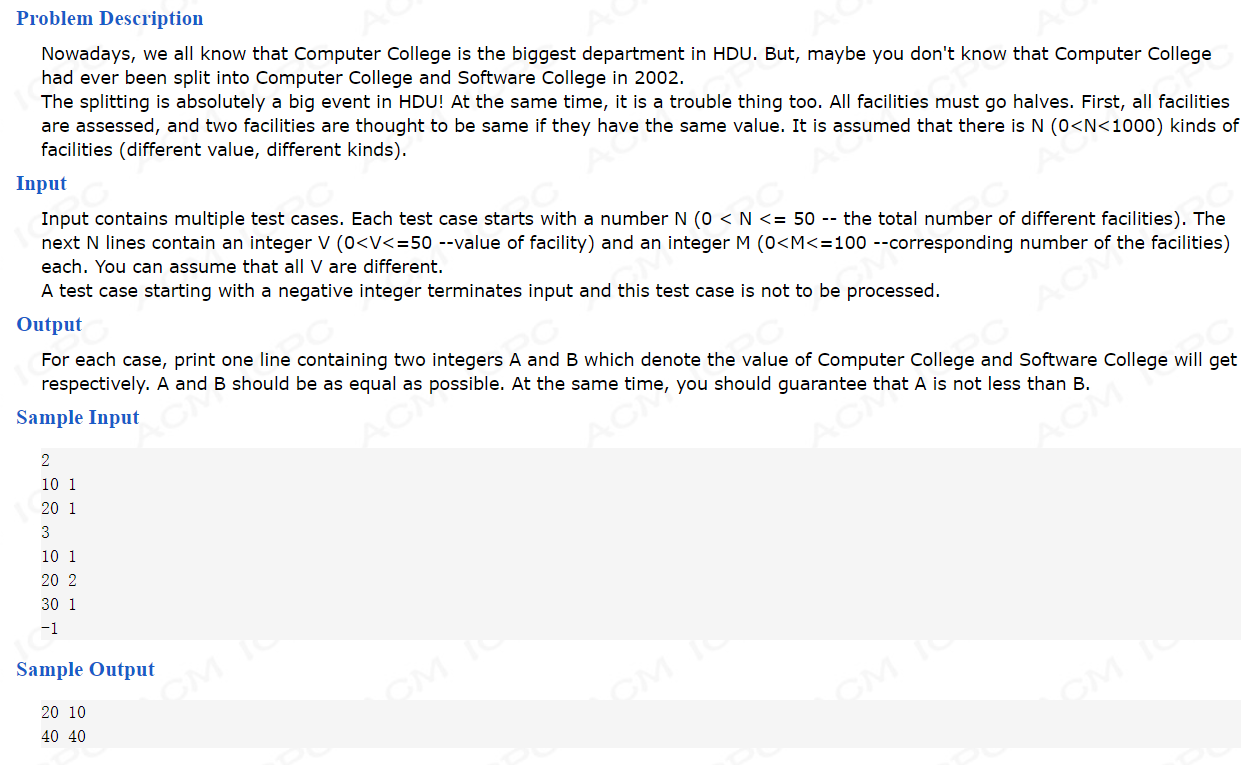
• 这个问题需要解决如何将物品分割，使得物品分隔相对均匀且A堆不小于B堆
  • 这同样是01背包问题，01背包问题可解决的是背包空间有限的情况下，所能获取到的最大资源的问题。
  • 该问题“背包的空间”即是物品的价值，如果我们求解出在总量一半约束下所能获取到的最大值即是B堆所能获取的最大值。
  • 该问题的思考：
    • 物品本身的价值可能就是代价，而不是有其他诸如重量的限制
    • 01背包问题能够解决代价有限的情况下的获取最大价值的问题

完全背包

• 思考方向与01背包类似，不同的是物品数量相对代价是无限的，只要条件允许就可以尝试放入背包中

  for(i=1;i<=N;i++)
  {
      for(j=space[i];j<=C;j++)
      {
          dp[j]=max(dp[j],dp[j-space[i]]+val[i]);
      }
  }
  

• 不同于01背包的逆序，完全背包为顺序，01背包在第i个物品时抉择取与不取时顺序会导致一个物品可能多次选取，在抉择序列位置靠后时前序记录已经被污染。

问题分析

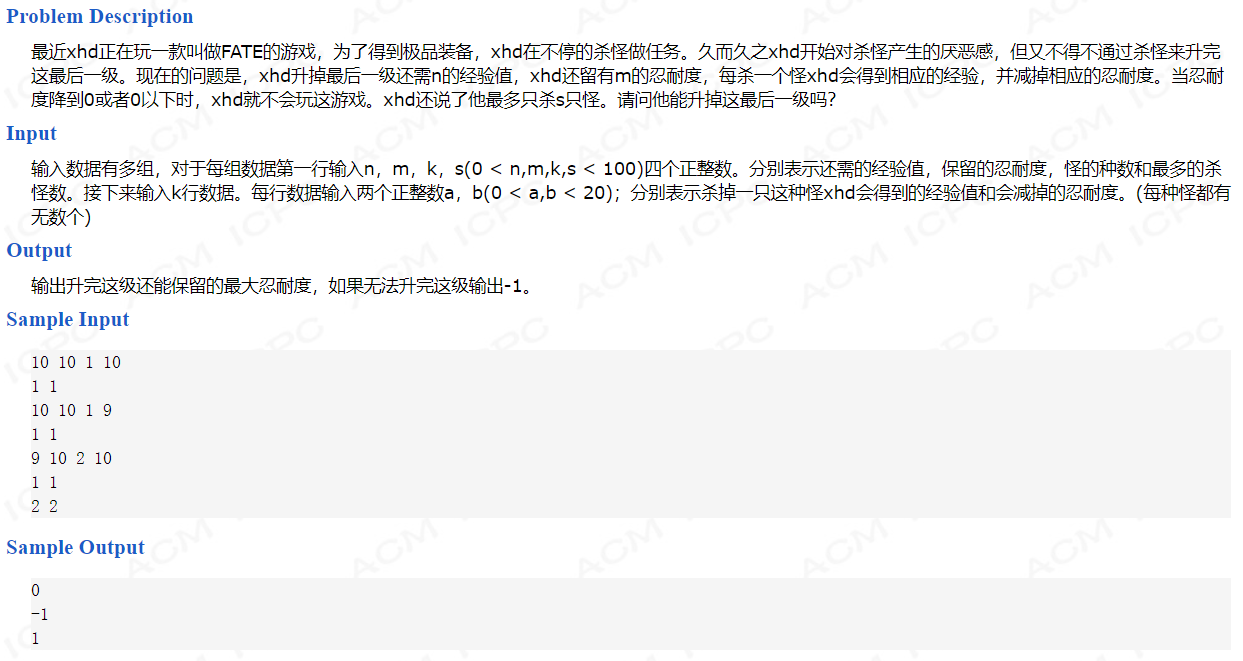
• 在这个问题中存在着双重限制，即杀怪的数量与忍耐度，目标是获取达成目标经验的最小耐力损耗

• 思考过程：

  • 分解问题，我们能否获得符合要求的所有结果，然后从中获取最小的耐力损耗

  • 启发之处在于背包问题能够解决一定代价限制下的最优解问题，又存在两方限制，即对代价需要两重循环，再加上是完全背包，所以代价为两重顺序循环，只要或得到经验超过目标经验既可以加入结果集中找出其中耐力损耗最小者。

  • 核心代码：

    for (int i = 0; i < k; i++) {
        for (int j = monster[i][1]; j <= m; j++) { //耐力代价
            for (int l = 1; l <= s; l++) { //数量代价
                dp[j][l] = Math.max(dp[j][l], dp[j - monster[i][1]][l - 1] + monster[i][0]);
                if (dp[j][l] >= n){ //符合的最小值
                    ans = Math.min(ans,j);
                }
            }
        }
    }
    

二进制背包优化

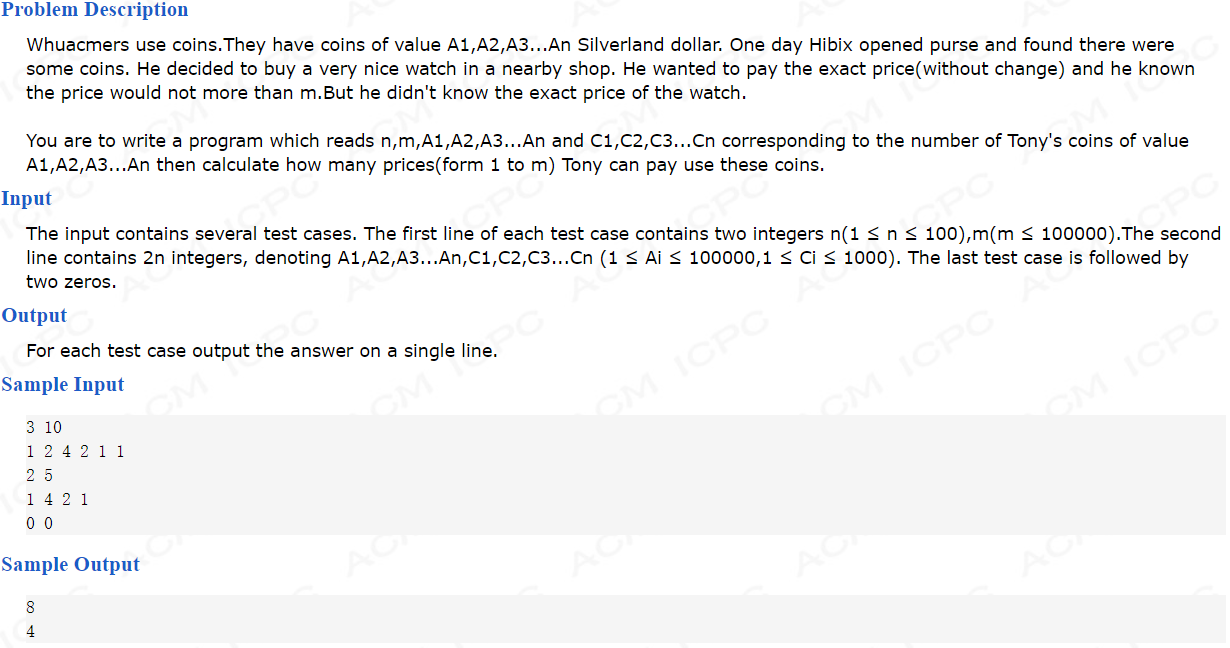
• 本问题需通过组合硬币获取最大组合数

• 若设硬币价值为约束，则能获取到某一价值约束下的最大值，而可能的最大值就为约束，当最大值与价值约束(背包空间)相等时即为一种情况

• 在本问题中存在存在一个优化：

  • 如果我们将硬币分散计算每一枚硬币的置入状态问题规模为：A1 * C1，若使用二进制优化，将优化到log(A1 * C1)的水平。

  • 当硬币总价值不小于背包空间时是为完全背包，此时可以使用二进制优化：n = 1 + 2 + 4 +...+k,我们只需要组合1，2，4，...,k即可以实现0~n内的所有选取组合，如：3 = 1 + 2。

  • 代码实现：

    private static void multiplePack(int value, int count) {
        if (value * count >= m) {
            completePack(value);
        } else {
            int i = 1;
            while (i <= count) {
                zero_one_Pack(i * value);
                count -= i;
                i = i << 1;
            }
            zero_one_Pack(count * value);
        }
    }
    private static void zero_one_Pack(int value) { //01背包的逆序
        for (int i = m; value != 0 && i >= value; i--) {
            dp[i] = Math.max(dp[i], dp[i - value] + value);
        }
    }
    private static void completePack(int value) { //完全背包的顺序
        for (int i = value; value != 0 && i <= m; i++) {
            dp[i] = Math.max(dp[i], dp[i - value] + value);
        }
    }