螺旋队列-打印-查找-步数解法-边界解法
1. 简述
螺旋队列也是常考题目之一,被程序员面试宝典收录了。这里写一写我对螺旋队列的理解,两种螺旋队列,两种操作。
两种队列的不同点是:一个从左上角开始扩展,一个从中间开始扩展。相同点是:初始点的数值都是1,数值逐渐增加,而且都是沿着右下左上的顺序进行扩展的。螺旋队列举例,如下所示:
第一种螺旋队列: 第二种螺旋队列:
1 2 3 4 7 8 9 10
12 13 14 5 6 1 2 11
11 16 15 6 5 4 3 12
10 9 8 7 16 15 14 13
两种操作,打印和查找。打印:指定矩阵长度N,将矩阵打印出来,例如指定N=4,就要输出上面的矩阵。查找:螺旋队列中数值为1的元素所在的左边认为是(0,0),给出一个坐标(x,y)找到该坐标位置上的值,例如指定坐标为(2,2),第一个队列返回的值为15,第二个队列返回的值为13。
2. 第一种螺旋队列
一般考察的是打印操作。使用模拟的方法,开辟一个A[N][N]的数组,按照数值的顺序,逐个将1,2,3,...,N*N放到数组的合适位置中。放置的方法就是,先把1放进去,然后先向右走,可以走就放进去,不能走就转向下走,直到不能走就向左,然后向上,最后再向右依次类推。判断能不能走可以使用四个边界,比如RightBound,初始值是3,即从A[0][0],最多可以走到A数值4的位置,此后修改RightBound的值为2,因为下次做多走到数值14的位置,其他方向的初始值类似。
对于N的初始值,向左的边界为0,向上的边界为1,向右的边界为N-1,向下的边界为N-1。注意上边界初始不能是0,否则就又回到原点了,会出现错误的。
using namespace std;
#define N 5
#define RIGHT 0
#define DOWN 1
#define LEFT 2
#define UP 3
int main() {
int A[N][N];
// get A
int RightBound,DownBound,LeftBound,UpBound;
RightBound = N-1; DownBound = N-1; LeftBound = 0; UpBound = 1; // 注意UpBound初始值为1
int direction, x, y, value, maxValue;
A[0][0] = 1; x = y = 0; value = 1; direction = RIGHT; maxValue =N*N;
while(value <= 24) { // 结束值不能错,否则会产生错误的
switch(direction) {
case RIGHT:
if(y+1 > RightBound) {
direction = (direction+1) % 4;
RightBound--;
}
else
A[x][++y] = ++value;
break;
case DOWN:
if(x+1 > DownBound) {
direction = (direction+1) % 4;
DownBound--;
}
else
A[++x][y] = ++value;
break;
case LEFT:
if(y-1 < LeftBound) {
direction = (direction+1) % 4;
LeftBound++;
}
else
A[x][--y] = ++value;
break;
case UP:
if(x-1 < UpBound) {
direction = (direction+1) % 4;
UpBound++;
}
else
A[--x][y] = ++value;
break;
}
// cout << x << ", " << y << ", direction:" << direction <<endl;
}
// print A
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
if(A[i][j] < 10)
cout << " " << A[i][j] << " ";
else
cout << A[i][j] << " ";
}
cout << endl;
}
system("PAUSE");
return 0;
}
输出结果如下:
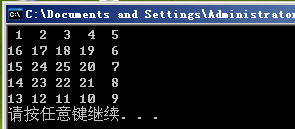
对于查找问题,可以直接把能够包含指定坐标的矩阵构造出来,然后把坐标上的值返回,比如指定坐标为(4,5),那么矩阵N=max{4,5}+1=6,开辟一个int A[6][6]的数组,把数值填充好了,然后返回A[4][5]就好了。不过这样会浪费很大的存储的空间,实际上,构造矩阵的过程中,每次根据方向和方向界限可以得到坐标和数值的对应,因此,不用开辟A[6][6],循环部分保留,每次检查一下当前坐标是否是指定的坐标,如果是的话,就把对应数值输出,否则继续循环。
由于在循环中,数值和坐标是对应产生的,实际上如果题目变为给数值,找坐标,也是一样的。
考察具体分有三种:打印矩阵,给坐标找数值,给数值找坐标,核心在于预测队列的从(0,0)开始的每一步的坐标,因为矩阵的长度和每一步的数值都十分要预测,下一步坐标是通过右左下上的顺序和对应边界的更新实现的。
3. 第二种螺旋队列
前面已经分析了,无论是打印矩阵,还是给坐标找数值,还是给数值找坐标,管家你是预测队列从(0,0)开始的每一步的坐标。第一种螺旋队列的预测是一种模拟的方法,即试着取走,如果碰过边界就转方向。第二种螺旋队列的预测,我还不知道怎么进行模拟,不过有公式可以用,即方向是右下左上,步数依次是1,1,2,2,3,3,4,4,5,5...。
另外螺旋队列打印的话,需要首先计算一下中心的坐标,所以对于这种队列,题目一般考察给坐标预测值,降低了程序的复杂度。
代码实现:
using namespace std;
#define N 4
#define RIGHT 0
#define DOWN 1
#define LEFT 2
#define UP 3
bool check(int x,int y, int index_x, int index_y) {
return (x==index_x&&y==index_y);
}
int main() {
int RightNum, DownNum, LeftNum, UpNum;
RightNum = DownNum = 1;
LeftNum = UpNum = 2;
int index_x = 2, index_y = 1; // 坐标(2,1)
int value, x, y, direction;
x = y = 0; direction = RIGHT; value = 1;
bool found = check(x,y,index_x,index_y); // 检查一下初始点
while(!found) {
if(value >= 25)
break;
switch(direction) {
case RIGHT:
for(int i=0; i<RightNum; i++) {
++x; ++value;
found = check(x,y,index_x,index_y);
if(found)
break;
}
RightNum += 2;
direction = (direction + 1) % 4;
break;
case DOWN:
for(int i=0; i<DownNum; i++) {
--y; ++value;
found = check(x,y,index_x,index_y);
if(found)
break;
}
DownNum += 2;
direction = (direction + 1) % 4;
break;
case LEFT:
for(int i=0; i<LeftNum; i++) {
--x; ++value;
found = check(x,y,index_x,index_y);
if(found)
break;
}
LeftNum += 2;
direction = (direction + 1) % 4;
break;
case UP:
for(int i=0; i<UpNum; i++) {
++y; ++value;
found = check(x,y,index_x,index_y);
if(found)
break;
}
UpNum += 2;
direction = (direction + 1) % 4;
break;
}
}
cout << value << endl;
system("PAUSE");
return 0;
}
输出结果为:10。
4. 重点分析
4.1 x,y随方向的变化
第一个螺旋队列,坐标原点在左上角,x,y是数组的下标,x表示数组行,是纵坐标,y表示数组列,是横坐标。向右++y,向左--y,向上--x,向下++x。
第二个螺旋队列,坐标原点在右下角,x表示横坐标,y表示纵坐标。向右++x,向左--x,向上++y,向下--y。
4.2 边界与步数
第一个队列用的是边界和方向,第二个队列用的是步数与方向,实际上这两种方法在两个队列上都可以用。
· 第一个队列边界+方向
从(0,0)开始,方向顺序为右下左上,初始边界为RighBound=N-1,DownBound=N-1,LeftBound=0,UpBound=1,边界更新为RightBound--,DownBound--,LeftBound++,UpBound++。
· 第一个队列步数+方向
从(-1,0)开始,方向顺序为右上左下,初始步数N,N-1,N-1,N-2,N-2,步数更新每次递减2。以N=4为例,步数序列为4,3,3,2,2,1,1,1。
· 第二个队列边界+方向
从(0,0)开始,方向顺序为右下左上,初始边界为RightBound=1,DownBound=1,LeftBound=-1,UpBound=-1,边界更新为RightBound++,DownBound++,LeftBound--,UpBound--。
· 第二个队列步数+方向
从(0,0)开始,方向顺序为右下左上,初始步数1,1,2,2,步数更新每次递增2。以N=4为例,步数序列为1,1,2,2,3,3,4。
5. 参考
程序员面试宝典(第二版)92页
螺旋矩阵的算法 http://www.cppblog.com/issayandfaye/archive/2009/11/15/100976.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号