第10章 树

树

树的定义与性质

无向树

• 无向树、森林的定义：
  
• 无向树的等价定义（或者性质）：
  

任意非平凡树$T=(n,m)$都至少有两片叶（使用握手定理和树的性质m=n-1可证）

生成树

生成树

• 定义：（注意树是生成子图）
  
• 生成树存在的充要条件：一个图$G=<V,E>$存在生成树$T_G=<V_T,E_T>$的充分必要条件是$G$是连通的
• 求连通图中生成树的方法：
  • 破圈法：每次删除回路中的一条边直到无回路。其删除的边的总数为m-n+1
  • 避圈法：每次选取G中一条与已选取的边不构成回路的边。选取的边的总数为n—1
  • 广度优先搜索算法：
    

使用广度优先搜索求生成树的例子：

最小生成树

最小生成树：

• 定义：
  
• 构造方法：
  • Kruskal算法：避圈选小边
    
  • Prim算法：无需避圈，选小邻边（选邻接点）
    

根树

根树的定义与分类

有向树：一个有向图，若略去所有有向边的方向所得到的无向图是一棵树，则这个有向图称为有向树
根树

• 定义：（平凡树不是根树）
  
  
• 画法：使用“倒置法”，可以省去全部箭头，不会发生误解，例：
  

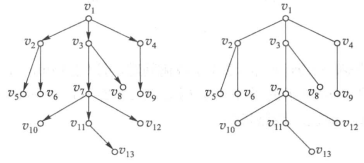
有序树：如果在根树中规定了每一层上结点的次序，这样的根树称为有序树
k元树

• 定义：
  
• k元完全树中分支点与叶结点数目之间的关系：
  在k元完全树中，若叶数为$t$，分支点数为$i$，则有$(k-1)\times i=t-1$.（可用握手定理和树的性质m=n-1证明）

根树的遍历

3种遍历方式：先序、中序、后序
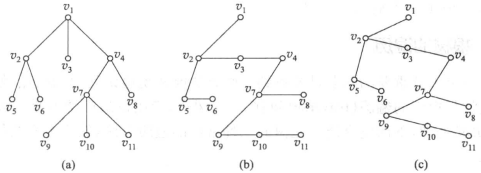
根树转二元树：即构造兄弟孩子树

例如：（a,b,c对应转换过程）

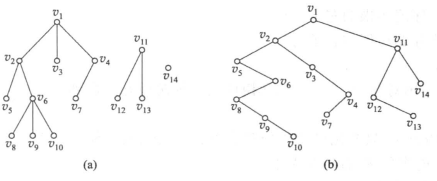
森林转二元树：将每个树的根视作兄弟，然后运用“根树转二元树”的方法

例如：（a,b对应转换过程）

最优树与赫夫曼算法（哈夫曼算法）

即构造哈夫曼树
多用于解决的问题：识别不同频率的东西，使得时间最优/最少

前缀和前缀码：

最优树：

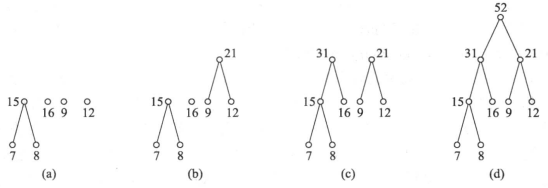
构造哈夫曼树：（权值均不同则哈夫曼树唯一，否则不唯一）

哈夫曼树构造例子：

根树的应用

波兰符号法与逆波兰符号法：

• 中序遍历算式树：中缀符号法
• 先序遍历算式树：前缀符号法（波兰符号法）
• 后序遍历算式树：后缀符号法（逆波兰符号法）

决策树：在决策树中，分支点是问题，分支是问题的选择，叶子是决策
关键道路法：

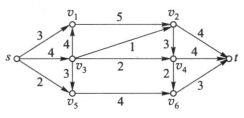
• 事件活动拓扑图：是有向无环图，其中顶点表示事件，边表示活动，活动进行的条件是事件已开始，事件开始的条件是该事件之前的活动均已完成
• 关键道路/PERT图/最长道路：完成所有任务的最关键（没有时间缓冲）路径（有一条或多条）
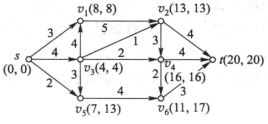
• 关键道路算法：计算每个事件的最早发生时间$ve(k)$：$ve(k)=Max\{ve(j)+w(v_j,v_k)\}$，计算时得到$ve(t)$的路径即关键路径
  或者采用书上的做法：
  

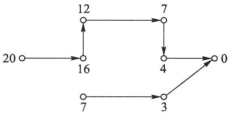
寻找关键路径例子：



其中可见关键路径为$P=sv_3v_1v_2v_4t$