概率论笔记（5）

第五章 大数定律与中心极限定理

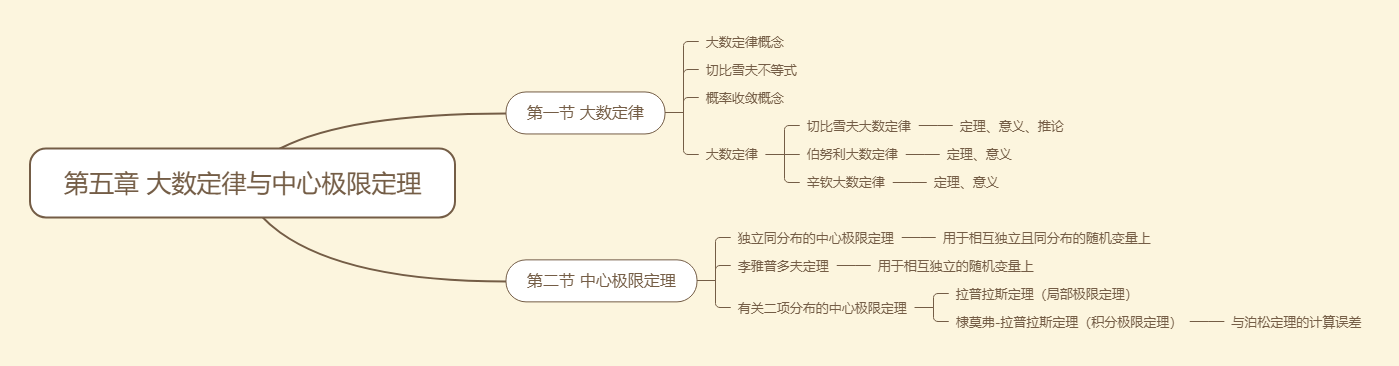
第一节 大数定律

大数定律概念：概率论中用来阐明大量随机现象的平均值的稳定性的一系列定律

切比雪夫不等式：

设随机变量\(X\)存在有限方差\(D(X)\)，则对任意\(\varepsilon >0\),有
\(P\left \{ \left | X-E(X) \right |\geq \varepsilon \right \}\leq \frac{D(X)}{\varepsilon ^{2}}\)

概率收敛：

设\(Y_{1},Y_{2},...,Y_{n},...\)是一个随机变量序列，\(a\)是一个常数，若对于任意正数\(\varepsilon\)，有
\(\lim_{n\rightarrow \infty}P\left \{ |Y_{n}-a|<\varepsilon \right \}=1\)
则称序列$$依概率收敛于\(a\)，记为\(Y_{n}\overset{P}{\rightarrow}a\)

切比雪夫大数定律：

设\(X_{1},X_{2},...\)是相互独立的随机变量序列，各有数学期望\(E(X_{1}),E(X_{2}),...\)及方差\(D(X_{1}),D(X_{2}),...\)
并且对于所有\(i=1,2,...\)都有\(D(X_{i})<l\)，其中l是与i无关的常数，则对任给的\(\varepsilon >0\)有
\(\lim_{n\rightarrow \infty}P\left \{ \left | \frac{1}{n}\sum_{i=1}^{n}X_{i}-\frac{1}{n}\sum_{i=1}^{n}E(X_{i}) \right |<\varepsilon \right \}=1\)

• 意义：当n充分大时随机变量\(Y=\frac{\sum_{i=1}^{n}X_{i}}{n}\)的离散程度是很小的
• 推论：
  设随机变量\(X_{1},X_{2},...,X_{n},...\)相互独立，且具有相同的数学期望和方差：
  \(E(X_{k})=\mu,D(X_{k})=\sigma ^{2},k=1,2,...\)
  作前n个随机变量的算术平均\(Y_{n}=\frac{1}{n}\sum_{k=1}^{n}X_{k}\)，则对于任意正数\(\varepsilon\)，有
  \(\lim_{n\rightarrow \infty}P\left \{ \left | Y_{n}-\mu \right |<\varepsilon \right \}=1\)

伯努利大数定律：

设\(n_{A}\)是n次独立重复试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则对于任意正数\(\varepsilon\)，有
\(\lim_{n\rightarrow \infty}P\left \{ \left | \frac{n_{A}}{n}-p \right |<\varepsilon \right \}=1\)

• 意义：试验的次数很大时，就可以用事件发生的频率代替事件发生的概率

辛钦大数定律：

设随机变量\(X_{1},X_{2},...,X_{n},...\)相互独立，服从同一分布，且具有数学期望\(E(X_{k})=\mu, k=1,2,...\)，则对于任意正数\(\varepsilon\)，有
\(\lim_{n \to \infty}P\left \{ \left | \frac{1}{n}\sum_{k=1}^{n}X_{k}-\mu \right |<\varepsilon \right \}=1\)

• 意义：当n足够大时，取\(\frac{1}{n}\sum_{i=1}^{n}X_{i}\)作为a的近似值，可以认为所发生的误差是很小的

第二节 中心极限定理

中心极限定理概念：有关论证 独立随机变量之和的极限分布 是 正态分布 的一系列定理

独立同分布的中心极限定理：

设随机变量\(X_{1},X_{2},...,X_{n},...\)相互独立，服从同一分布，且具有数学期望和方差
\(E(X_{k})=\mu ,D(X_{k})=\sigma ^{2}\neq 0, k=1,2,...\)
则随机变量
\(Y_{n}=\frac{\sum_{k=1}^{n}X_{k}-E(\sum_{k=1}^{n}X_{k})}{\sqrt{D(\sum_{k=1}^{n}X_{k})}}=\frac{\sum_{k=1}^{n}X_{k}-n\mu}{\sqrt{n}\sigma }\)
的分布函数\(F_{n}(x)\)对于任意x，满足：
\(\lim_{n \to \infty}F_{n}(x)=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^{2}}{2}}dt\)
所以当n充分大时，近似有
\(Y_{n}=\frac{\sum_{k=1}^{n}X_{k}-n\mu}{\sqrt{n\sigma ^{2}}}\sim N(0,1)\)，或
\(\sum_{k=1}^{n}X_{k} \sim N(n\mu ,n\sigma ^{2})\)

李雅普多夫定理：

设随机变量\(X_{1},X_{2},...,X_{n},...\)相互独立，它们具有数学期望和方差：
\(E(X_{k})=\mu ,D(X_{k})=\sigma ^{2}\neq 0, k=1,2,...\)
记\(B_{n}^{2}=\sum_{k=1}^{n}\sigma _{n}^{2}\)，若存在正数\(\delta\)，使得当\(n \to \infty\)时，
\(\frac{1}{B_{n}^{2+\delta }}\sum_{k=1}^{n}E\left \{ \left | X_k-\mu _{k} \right |^{2+\delta } \right \}\rightarrow 0\)
则随机变量
\(Z_{n}=\frac{\sum_{k=1}^{n}X_{k}-E(\sum_{k=1}^{n}X_{k})}{\sqrt{D(\sum_{k=1}^{n}X_{k})}}=\frac{\sum_{k=1}^{n}X_{k}-\sum_{k=1}^{n}\mu _{k}}{B_{n}}\)
的分布函数\(F_{n}(x)\)对于任意x，满足
\(\lim_{n \to \infty}F_{n}(x)=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^{2}}{2}}dt\)

• 意义：
  当n很大时，随机变量\(Z_{n}\)近似服从正态分布N(0,1)
  即\(\sum_{k=1}^{n}X_{k}=B_{n}Z_{n}+\sum_{k=1}^{n}\mu_{k}\)近似服从正态分布\(N\left ( \sum_{k=1}^{n}\mu_{k},B_{n}^{2} \right )\)
  （PS：感觉是独立同分布的中心极限定理的扩展）

有关二项分布的中心极限定理：

设X服从参数为n，p的二项分布，则

• 拉普拉斯定理（局部极限定理）：
  当\(n \to \infty\)时
  \(P\left \{ X=k \right \}=\frac{1}{\sigma}\varphi \left ( \frac{k-\mu}{\sigma} \right )\)
  其中\(\mu=np,\sigma=\sqrt{np(1-p)},k=0,1,2,...,n,\varphi (x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2}}\)
• 棣莫弗-拉普拉斯定理（积分极限定理）：
  对于任意的x，恒有
  \(\lim_{n \to \infty}P\left \{ \frac{X-\mu}{\sigma }\leq x \right \}=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2}}dt\)
  其中\(\mu=np,\sigma=\sqrt{np(1-p)}\)

棣莫弗-拉普拉斯定理与泊松定理：

正态分布和泊松分布均是二项分布的极限分布，但后者以\(n \to \infty, p \to 0, np \to \lambda\)为条件，前者只要求\(n \to \infty\)
所以一般当n很大p很小时，二项分布用正态分布近似计算不如泊松分布准确