数据库系统概论笔记（2）

第二章 关系数据库

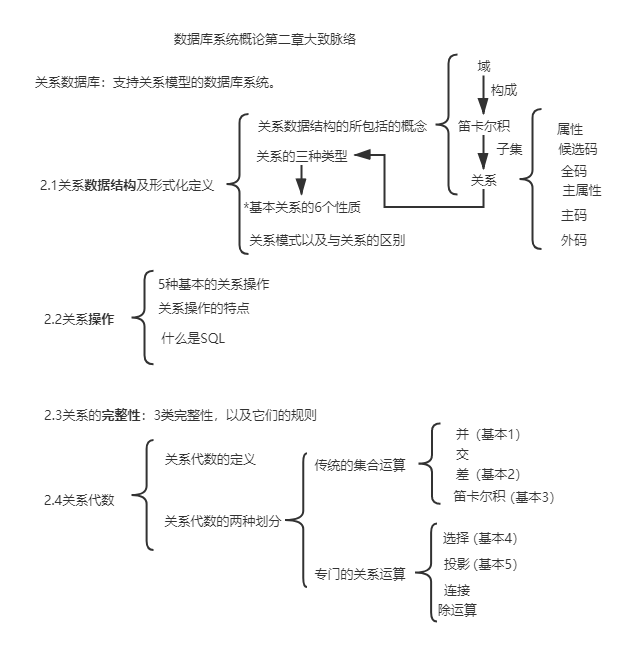
关系数据库：支持关系模型的数据库系统。

2.1关系数据结构及形式化定义

关系：

• 域：一组具有相同数据类型的值的集合。（蕴含列的取值范围）
• 域的基数：一个域允许的不同取值个数。
• 笛卡尔积：（域上的集合运算）
  所有域（\(D_{1},D_{2},...,D_{n}\)）所有取值的组合（一个组合是一个元组，元组中有n个分量（值）称为n元组）
  组合不能重复（不允许冗余）
• 关系：笛卡尔积的有限子集称为在域\(D_{1},D_{2},...,D_{n}\)上的关系。
  一般表示为\(R(D_{1},D_{2},...,D_{n})\)（\(R\)是关系的名字，\(n\)是关系的目或度，n为多少就称为n元关系）
  关系中的每个元素是关系中的元组，通常用\(t\)来表示。
  属性：每列的名字，用来区分域（域可以相同，属性一定不同）
  候选码：某一最少属性组的值能唯一标识一个元组。（候选码可以有多个）
  全码：关系模式的所有属性组成该关系模式的候选码。
  主属性：候选码的所有属性称为主属性，不在任何候选码内的属性称为非主属性。
  主码：在多个候选码中选定其中一个为主码。
  外码：设\(F\)是基本关系R的一个或一组属性，但不是关系\(R\)的码，\(K_{s}\)是基本关系\(S\)的的主码，若\(F\)与\(K_{s}\)相对应，则称\(F\)是\(R\)的外码。（\(R\)是参照关系，\(S\)是被参照关系，两者可以为同一关系）
  外码是用来和其他表建立联系用的，当然建立连接也可以不用外键

关系的三种类型：基本关系（基本表/基表）、查询表、视图表。

• 基本关系：实际存在的表（实际存储数据的逻辑表示）。
• 查询表：查询结果对应的表。
• 视图表：由基本表或其他视图表导出的表（虚表）。

基本关系的6个性质：

1. 列是同质的
2. 一域可有多列，一列即一属性，不同列属性名不同。
3. 行顺序无所谓
4. 列顺序无所谓
5. 任意两个元组的候选码不能取相同的值。
6. 分量必须取原子值。（关系第一范式（规范化的关系称为范式））

关系模式：关系的描述，可表示为\(R(U,D,DOM,F)\)

• \(R\)：关系名
• \(U\)：组成该关系的属性名集合
• \(D\)：\(U\)中属性所来自的域
• \(DOM\)：属性到域的映像集合
• *\(F\)：属性间数据的依赖关系集合

关系数据库的值是关系模式在某一时刻对应的关系的集合，通常就称为关系数据库。
关系模式是稳定的，关系是变化的

2.2关系操作

5种基本的关系操作：选择、投影、并、差、笛卡尔积。
关系操作特点：集合操作方式，操作的对象和结果都是集合。
*早期的关系操作能力通常用代数方式或逻辑方式来表示，分别称为关系代数和关系演算。
SQL：结构化查询语言

2.3关系的完整性

三类完整性约束：实体完整性、参照完整性、用户定义完整性。（前两个是必须满足的，称为关系的两个不变性）

实体完整性规则：主属性的值不能取空值。（空值包括不存在/无意义/未知）
参照完整性规则：每一个元组在外码F上的值 或为空值 或等于S中某个元组的主码值。（外码F对应基本关系S的主码）
用户定义的完整性：针对某一具体关系数据库的约束条件。

2.4关系代数

关系代数：一种抽象的查询语言，用关系的运算表达查询
关系代数按运算符的不同可分为

• 传统的集合运算（从行的角度进行）
• 专门的关系运算（涉及行和列）
  

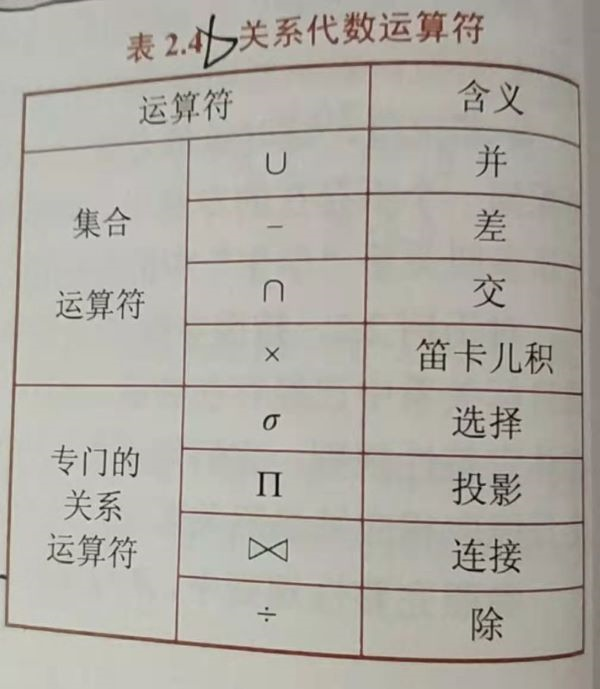
传统的集合运算：

（交并差操作要求 目数相同 且 属性取自同一个域（可比））

• 并：关系\(R\)与关系\(S\)的并，记作：\(R\cup S=\left\{ t|t\in R\vee t\in S \right\}\)
• 差：关系\(R\)与关系\(S\)的差，记作：\(R-S=\left\{ t|t\in R\wedge t\notin S \right\}\)
• 交：关系\(R\)与关系\(S\)的交，记作：\(R\cap S=\left\{ t|t\in R\wedge t\in S \right\}\)（也可以表示成\(R\cap S=R-(R-S)\)）
• 笛卡尔积：关系\(R\)与关系\(S\)的笛卡尔积（广义），记作：\(R\times S=\left\{ \widehat{t_{r}t_{s}}|t_{r}\in R\wedge t_{s}\in S \right\}\)

专门的关系运算：

\(t[A_{i}]\)：元组\(t\)（某行） 相应于 属性\(A_{i}\)的一个分量（某列）。
\(t[A]=(t[A_{i1}],t[A_{i2}],...,t[A_{ik}])\)表示元组t（某行） 在属性列（属性组）\(A=\left\{A_{i1},A_{i2},...,A_{ik}\right\}\)上诸分量（多列） 的集合。（\(t[\overline{A}]\)同理）
\(\widehat{t_{r}t_{s}}\)：元组\(t_{r}\)和\(t_{s}\)的连接（串接）。（\(t_{r}\in R,t_{s}\in S\)，若\(R\)为\(m\)目\(S\)为\(n\)目，则\(\widehat{t_{r}t_{s}}\)为\(m+n\)目）
象集：\(R\)中属性组\(X\)上值为\(x\)的诸元组在\(Z\)上分量的集合，记为\(Z_{x}=\left\{t[Z]\mid t\in R, t[X]=x\right\}\)

• 选择（限制）：关系\(R\)中满足给定条件的诸元组，记作\(\sigma _{F}(R)=\left\{t\mid t\in R \wedge F(t)='真'\right\}\)。（行的角度）
  （\(F\)表示选择条件，是一个逻辑表达式，基本形式为\(X_{1}\theta Y_{1}\)，\(\theta\)是比较运算符（“不等于”表达为“\(<>\)”其它一样），另外可用逻辑运算符\(乛,\wedge ,\vee\)）
• 投影：从\(R\)中选择出若干属性列组成新的关系，记作\(\prod _{A}(R)=\left\{t[A]\mid t\in R\right\}\)（\(A\)为\(R\)中的属性列）（列的角度）
• 连接（\(\theta\)连接）：从两个关系的笛卡尔积中选取属性间满足一定条件的元组，记作\(R\Join S=\left\{\widehat{t_{r}t_{s}}\mid t_{r}\in R\wedge t_{s}\in S\wedge t_{r}[A]\theta t_{s}[B]\right\}\)（除了自然连接，其他都是行的角度）
  （\(A\)和\(B\)分别为\(R\)和\(S\)上列数相等且可比的属性组，\(\theta\)是比较运算符）
  等值相连：\(\theta\)为\(=\)的连接运算
  自然连接：一种特殊的等值连接，两个关系中进行比较的分量必须是同名的属性组
  悬浮元组：自然连接时，关系\(R\)（或关系\(S\)）上的某些元组因在关系\(S\)（或关系\(R\)）中找不到公共属性上值相等的元组而被舍弃，被舍弃的元组称为悬浮元组
  外连接（全连接）：把悬浮元组也保存在结果关系中，其他属性上填NULL，称为外连接。
  左外连接：只保留左边关系\(R\)中的悬浮元组。
  右外连接：只保留右边关系\(S\)中的悬浮元组。
• 除运算：给定关系\(R(X,Y)\)和\(S(Y,Z)\)，\(R.Y\)和\(S.Y\)出自相同域集，元组在\(X\)上分量值\(x\)的象集\(Y_{x}\)包含\(S\)在\(Y\)上投影的集合，记作\(R\div S=\left\{t_{r}[X]\mid t_{r}\in R\wedge \prod _{Y}(S)\subseteq Y_{x}\right\}\)（同时从行和列的角度进行运算）
  （关系\(R\)除以关系\(S\)的结果为关系\(T\)，则\(T\)包含所有在\(R\)但不在\(S\)中的属性及其值，且\(T\)的元组与\(S\)的元组的所有组合都在\(R\)中）

相关例子可以看书P56

关系运算的5种基本运算：并、差、笛卡尔积、选择、投影。（其它运算均可以用这5中基本运算来表达）

*2.5关系运算

略（不讲）