AP CSA algorithm notes

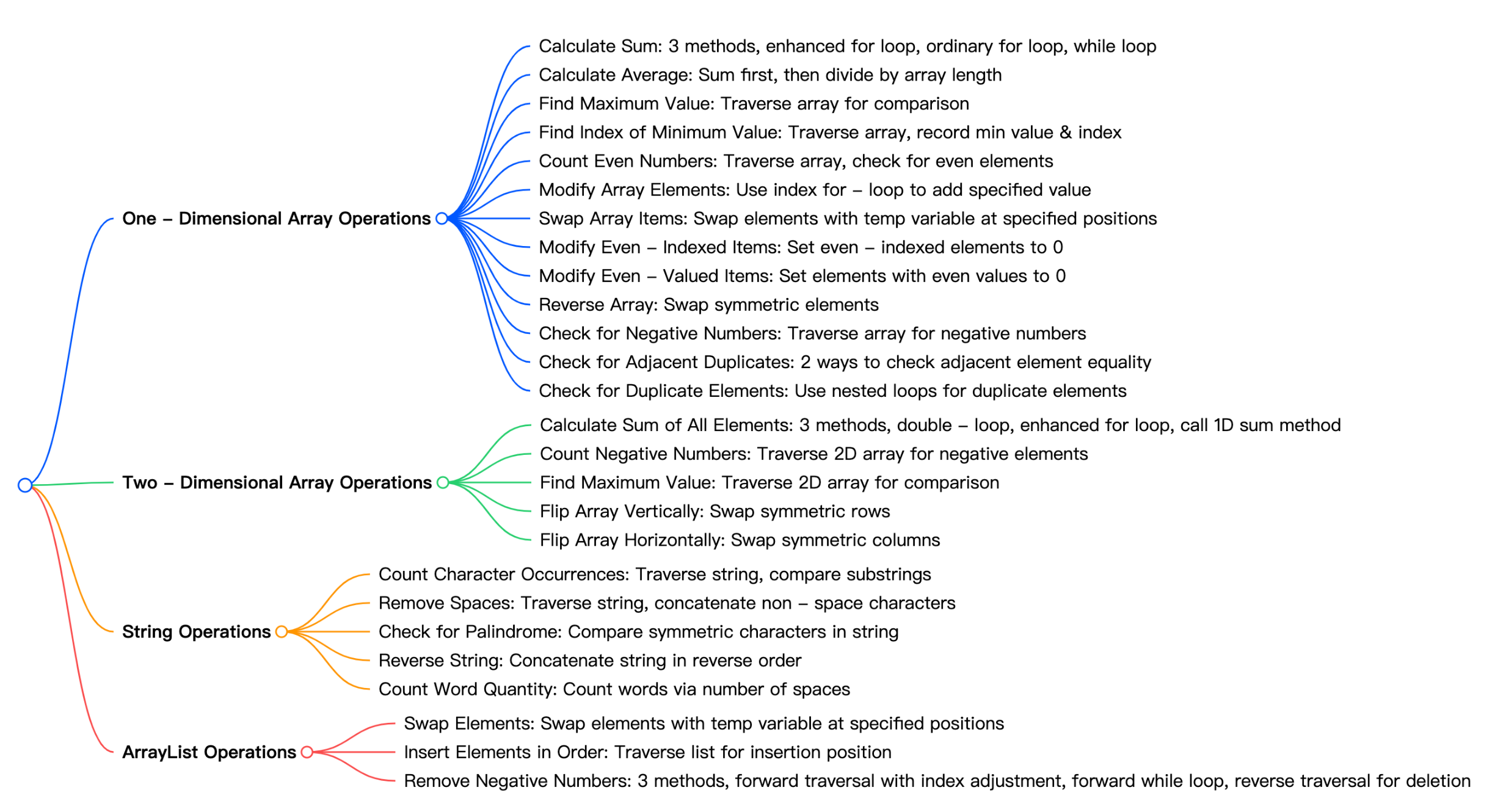
One - Dimensional Array Operations

• Calculate Sum: 3 methods, enhanced for loop, ordinary for loop, while loop
• Calculate Average: Sum first, then divide by array length
• Find Maximum Value: Traverse array for comparison
• Find Index of Minimum Value: Traverse array, record min value & index
• Count Even Numbers: Traverse array, check for even elements
• Modify Array Elements: Use index for - loop to add specified value
• Swap Array Items: Swap elements with temp variable at specified positions
• Modify Even - Indexed Items: Set even - indexed elements to 0
• Modify Even - Valued Items: Set elements with even values to 0
• Reverse Array: Swap symmetric elements
• Check for Negative Numbers: Traverse array for negative numbers
• Check for Adjacent Duplicates: 2 ways to check adjacent element equality
• Check for Duplicate Elements: Use nested loops for duplicate elements

Two - Dimensional Array Operations

• Calculate Sum of All Elements: 3 methods, double - loop, enhanced for loop, call 1D sum method
• Count Negative Numbers: Traverse 2D array for negative elements
• Find Maximum Value: Traverse 2D array for comparison
• Flip Array Vertically: Swap symmetric rows
• Flip Array Horizontally: Swap symmetric columns

String Operations

• Count Character Occurrences: Traverse string, compare substrings
• Remove Spaces: Traverse string, concatenate non - space characters
• Check for Palindrome: Compare symmetric characters in string
• Reverse String: Concatenate string in reverse order
• Count Word Quantity: Count words via number of spaces

ArrayList Operations

• Swap Elements: Swap elements with temp variable at specified positions
• Insert Elements in Order: Traverse list for insertion position
• Remove Negative Numbers: 3 methods, forward traversal with index adjustment, forward while loop, reverse traversal for deletion

One-dimensional Array Operations

• There are 3 methods to calculate the sum of a one-dimensional array.
• The average value of a one-dimensional array can be calculated.
• The index of the minimum value in a one-dimensional array can be found.

Two-dimensional Array Operations

• There are 3 calculation methods to find the sum of a two-dimensional array.
• The number of negative numbers in a two-dimensional array can be counted.
• The two-dimensional array can be flipped vertically and horizontally.

String Processing

• The number of occurrences of characters and substrings in a string can be counted.
• Spaces in a string can be removed.
• Whether a string is a palindrome can be determined.

ArrayList Operations

• Two elements in an ArrayList can be swapped.
• An element can be inserted into an ordered ArrayList.
• Negative numbers in an ArrayList can be removed.

1. One - Dimensional Arrays

1. sumOfArray01(int[] arr):
   • Code:

public int sumOfArray01(int[] arr) { 
    int sum = 0; 
    for (int num : arr) 
        sum += num; 
    return sum; 
} 

• Explanation: This method calculates the sum of all elements in a one - dimensional array. It uses an enhanced for loop (foreach loop) to iterate through each element in the arr array and adds it to the sum variable. Finally, it returns the calculated sum.
• Comment: The enhanced for loop simplifies the iteration process, making the code more concise.

2. sumOfArray02(int[] arr):
   • Code:

public int sumOfArray02(int[] arr) { 
    int sum = 0; 
    for (int i = 0; i < arr.length; i++)
        sum += arr[i]; 
    return sum; 
} 

• Explanation: This is another way to calculate the sum of an array. It uses a traditional for loop with an index variable i. By accessing each element through the index i, it accumulates the values into the sum variable and returns the sum at the end.
• Comment: The traditional for loop gives more control over the iteration index, which can be useful in some cases.

3. sumOfArray03(int[] arr):
   • Code:

public int sumOfArray03(int[] arr) { 
    int sum = 0; 
    int i = 0; 
    while(i < arr.length ) { 
        sum += arr[i]; 
        i++; 
    } 
    return sum; 
}

• Explanation: This method uses a while loop to calculate the sum of the array elements. It initializes an index variable i to 0 and keeps adding the elements at index i to the sum variable while i is less than the length of the array. After the loop, it returns the sum.
• Comment: The while loop is more flexible when the iteration condition is more complex than a simple range - based iteration.

4. aveArray(int[] arr):
   • Code:

public double aveArray(int[] arr) { 
    int s = 0; 
    for (int i = 0; i < arr.length; i++) 
        s += arr[i]; 
    return (double) s / arr.length; 
}

• Explanation: First, it calculates the sum of all elements in the array, similar to the sum - calculating methods above. Then, it divides the sum by the length of the array to get the average. The result is cast to a double to ensure precision in case the sum and length values result in a non - integer average.
• Comment: Casting to double is crucial to avoid integer division truncation.

5. maxOfArray(int[] arr):
   • Code:

public int maxOfArray(int[] arr) { 
    int max = arr[0]; 
    for (int num : arr) 
        if (max < num) 
            max = num; 
    return max; 
}

• Explanation: It initializes the max variable with the first element of the array. Then, it iterates through each element in the array using an enhanced for loop. If an element is greater than the current max, it updates the max variable. Finally, it returns the maximum value found in the array.
• Comment: Initializing max with the first element is a common approach, but it may need to be adjusted if the array could be empty.

6. indexOfMin(int[] arr):
   • Code:

public int indexOfMin(int[] arr) { 
    int min = arr[0]; 
    int minIndex = 0; 
    for (int i = 1; i < arr.length; i++) 
        if (arr[i] < min) { 
            min = arr[i]; 
            minIndex = i; 
        } 
    return minIndex; 
}

• Explanation: This method finds the index of the smallest element in the array. It starts by assuming the first element is the minimum and stores its value in min and its index in minIndex. Then, it iterates through the remaining elements. If it finds an element smaller than the current min, it updates min and minIndex. At the end, it returns the index of the minimum element.
• Comment: It only works correctly when the array is not empty.

7. countEven(int[] arr):
   • Code:

public int countEven(int[] arr) { 
    int count = 0; 
    for (int num : arr) 
        if (num % 2 == 0) 
            count++; 
    return count; 
}

• Explanation: It iterates through each element in the array using an enhanced for loop. For each element, it checks if the element is even (using the modulo operator %). If it is even, it increments the count variable. Finally, it returns the count of even elements in the array.
• Comment: The modulo operator is a simple and effective way to check for even numbers.

8. addNum(int[] arr, int n):
   • Code:

public void addNum(int[] arr, int n) { 
    for (int i = 0; i < arr.length; i++) { 
        arr[i] += n; 
    } 
}

• Explanation: This method adds a given number n to each element in the arr array. It uses a traditional for loop to access each element by its index and updates the element by adding n to it.
• Comment: Remember that you can't use a foreach loop to modify the elements of an array directly.

9. swap(int[] arr, int i, int j):
   • Code:

public void swap(int[] arr, int i, int j) { 
    int temp = arr[i]; 
    arr[i] = arr[j]; 
    arr[j] = temp; 
}

• Explanation: This method swaps the elements at indices i and j in the arr array. It uses a temporary variable temp to hold the value of the element at index i so that it can be safely overwritten with the value at index j, and then the value in temp is assigned to the element at index j.
• Comment: Swapping elements is a common operation in sorting and other array - manipulation algorithms.

10. changeEven(int[] arr):

• Code:

public void changeEven(int[] arr) { 
    for (int i = 0; i < arr.length; i += 2)
        arr[i] = 0; 
}

• Explanation: This method changes all elements at even - numbered indices (0, 2, 4, etc.) in the arr array to 0. It uses a for loop with a step of 2 to access the even - indexed elements and assigns 0 to them.
• Comment: The step of 2 in the for loop is the key to accessing only the even - indexed elements.

11. changeEven(int[] arr) (overloaded method):

• Code:

public static void changeEven(int[] arr) 
    for (int i = 0; i < arr.length; i++) 
        if(arr[i] % 2 == 0) 
            arr[i] = 0; 
}

• Explanation: This overloaded method changes all elements in the arr array that are even to 0. It iterates through each element using a traditional for loop, checks if the element is even, and if so, assigns 0 to it.
• Comment: The overloading allows for different functionality based on the input requirements.

12. reverseArray(int[] arr):

• Code:

public void reverseArray(int[] arr) { 
    int mid = arr.length / 2; 
    for (int i = 0; i < mid; i++) { 
        int temp = arr[i]; 
        arr[i] = arr[arr.length - i - 1]; 
        arr[arr.length - i - 1] = temp; 
    } 
}

• Explanation: This method reverses the order of elements in the arr array. It calculates the middle index of the array. Then, it iterates from the start to the middle of the array. For each iteration, it swaps the element at index i with the element at the corresponding index from the end of the array (arr.length - i - 1).
• Comment: Reversing an array is a common operation in many algorithms.

13. hasNegtive(int[] arr):

• Code:

public static boolean hasNegtive(int[] arr){ 
    for(int i = 0; i < arr.length; i++) 
        if(arr[i] < 0) 
            return true;
    return false; 
}

• Explanation: This method checks if the arr array contains any negative elements. It iterates through each element in the array using a for loop. If it finds a negative element, it immediately returns true. If it reaches the end of the array without finding a negative element, it returns false.
• Comment: Early return improves the efficiency when a negative element is found quickly.

14. hasDuplicates(int[] arr) (first version):

• Code:

public static boolean hasDuplicates(int[] arr) { 
    for(int i = 0; i < arr.length - 1; i++) 
        if(arr[i] == arr[i + 1]) 
            return true; 
    return false; 
}

• Explanation: This method checks if there are any adjacent duplicate elements in the arr array. It iterates through the array until the second - last element. For each element, it checks if it is equal to the next element. If it finds a pair of adjacent equal elements, it returns true. Otherwise, it returns false when it reaches the end of the array.
• Comment: This version only checks for adjacent duplicates.

15. hasDuplicates(int[] arr) (second version):

• Code:

public static boolean hasDuplicates(int[] arr) { 
    for(int i = 1; i < arr.length; i++) 
        if(arr[i] == arr[i - 1]) 
            return true; 
    return false; 
}

• Explanation: Similar to the first version, but it starts iterating from the second element and checks if the current element is equal to the previous one. If a duplicate is found, it returns true; otherwise, it returns false at the end.
• Comment: Different starting points in the loop can be useful depending on the context.

16. hasDuplicates(int[] arr) (third version):

• Code:

public static boolean hasDuplicates(int[] arr) { 
    for(int i = 0; i < arr.length - 1; i++) { 
        for(int j = i + 1; j < arr.length; j++) 
            if(arr[i] == arr[j]) 
                return true; 
    } 
    return false; 
}

• Explanation: This method checks if there are any duplicate elements (not just adjacent) in the arr array. It uses a nested for loop. The outer loop iterates through each element, and the inner loop starts from the next element and checks if it is equal to the element in the outer loop. If a duplicate is found, it returns true. If no duplicates are found after checking all possible pairs, it returns false.
• Comment: The nested loop approach is less efficient for large arrays but checks for all possible duplicates.

2. Two - Dimensional Arrays

1. sumOfMat_1(int[][] mat):
   • Code:

public int sumOfMat_1(int[][] mat){
    int sum = 0; 
    for (int r = 0; r < mat.length; r++)
        for (int c = 0; c < mat[r].length; c++)
            sum += mat[r][c];
    return sum;
}

• Explanation: This method calculates the sum of all elements in a two - dimensional array mat. It uses a nested for loop. The outer loop iterates through each row, and the inner loop iterates through each column in the current row. For each element mat[r][c], it adds the value to the sum variable. Finally, it returns the sum of all elements.
• Comment: Nested loops are a common way to iterate through two - dimensional arrays.

2. sumOfMat_2(int[][] mat):
   • Code:

public int sumOfMat_2(int[][] mat){ 
    int sum = 0;
    for (int[] row : mat)
        for (int element : row)
            sum += element;
    return sum;
}

• Explanation: This method also calculates the sum of all elements in the two - dimensional array. It first uses an enhanced for loop to iterate through each row in the mat array. Then, for each row, it uses another enhanced for loop to iterate through each element in that row and adds it to the sum variable.
• Comment: Enhanced for loops simplify the code for iterating through rows and elements.

3. sumOfMat_3(int[][] mat):
   • Code:

public int sumOfMat_3(int[][] mat){
    int sum = 0;
    for (int[] row : mat)
        sum += sumOfArray(row);
    return sum;
}

• Explanation: This method calculates the sum of all elements in the two - dimensional array by using a previously defined sumOfArray method. It iterates through each row in the mat array using an enhanced for loop and adds the sum of each row (calculated by sumOfArray(row)) to the sum variable.
• Comment: Reusing existing methods can make the code more modular and easier to maintain.

4. countNegs(int[][] mat):
   • Code:

public static int countNegs (int[][] mat ) 
    int count = 0; 
    for (int[] row : mat) 
        for (int num : row) 
            if (num < 0) 
                count++; 
    return count; 
}

• Explanation: This method counts the number of negative elements in a two - dimensional array mat. It uses a nested enhanced for loop. The outer loop iterates through each row, and the inner loop iterates through each element in the current row. If an element is negative, it increments the count variable. Finally, it returns the count of negative elements.
• Comment: Nested enhanced for loops are convenient for iterating through two - dimensional arrays in this case.

5. maxOfTwoDArray(int[][] mat):
   • Code:

public int maxOfTwoDArray(int[][] mat) { 
    int max = mat[0][0]; 
    for (int[] row : mat) 
        for (int element : row) 
            if(element > max) 
                max = element; 
    return max; 
}

• Explanation: This method finds the maximum element in a two - dimensional array mat. It initializes the max variable with the first element of the array. Then, it uses a nested enhanced for loop to iterate through all elements in the array. If an element is greater than the current max, it updates the max variable. Finally, it returns the maximum value found.
• Comment: Initializing max with the first element assumes the array is not empty.

6. reverseRow_01(int[][] mat):
   • Code:

public void reverseRow_01(int[][] mat) { 
    for (int r = 0; r < mat.length/2; r++) { 
        int[] temp = mat[r]; 
        mat[r] = mat[mat.length - r - 1]; 
        mat[mat.length - r - 1] = temp; 
    } 
}

• Explanation: This method reverses the order of rows in a two - dimensional array mat. It iterates from the start to the middle of the number of rows. For each iteration, it swaps the current row with the corresponding row from the end of the array using a temporary array variable temp.
• Comment: Reversing rows can be useful in various matrix - related operations.

7. reverseCol_01(int[][] mat):
   • Code:

public void reverseCol_01(int[][] mat) {
    int mid = mat[0].length / 2; 
    for (int r = 0; r < mat.length; r++) { 
        for (int c = 0; c < mid; c++) { 
            int temp = mat[r][c]; 
            mat[r][c] = mat[r][mat[r].length - c - 1]; 
            mat[r][mat[r].length - c