基于python的数学建模---场线与数值解（微分方程）

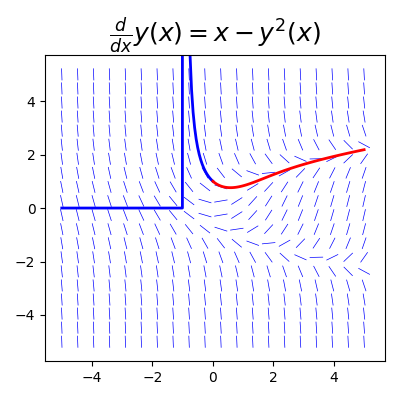
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
import sympy


def plot_direction_field(x, y_x, f_xy, x_lim=(-5, 5), y_lim=(-5, 5), ax=None):
    f_np = sympy.lambdify((x, y_x), f_xy, 'numpy')
    x_vec = np.linspace(x_lim[0], x_lim[1], 20)
    y_vec = np.linspace(y_lim[0], y_lim[1], 20)

    if ax is None:
        _, ax = plt.subplots(figsize=(4, 4))
    # dx相邻两值的距离
    dx = x_vec[1] - x_vec[0]
    dy = y_vec[1] - y_vec[0]

    for m, xx in enumerate(x_vec):
        for n, yy in enumerate(y_vec):
            Dy = f_np(xx, yy) * dx
            Dx = 0.8 * dx ** 2 / np.sqrt(dx ** 2 + Dy ** 2)
            Dy = 0.8 * Dy * dy / np.sqrt(dx ** 2 + Dy ** 2)
            ax.plot([xx - Dx / 2, xx + Dx / 2], [yy - Dy / 2, yy + Dy / 2], 'b', lw=0.5)

    ax.axis('tight')
    # y对x的偏导=f_xy
    ax.set_title(r"$%s$" % (sympy.latex(sympy.Eq(y_x.diff(x), f_xy))), fontsize=18)

    return ax


# 自变量
x = sympy.symbols('x')
# 因变量
y = sympy.Function('y')
f = x - y(x) ** 2

f_np = sympy.lambdify((y(x), x), f)
y0 = 1
xp = np.linspace(0, 5, 100)
# func  初始值 x的范围
yp = integrate.odeint(f_np, y0, xp)
xn = np.linspace(0, -5, 100)
yn = integrate.odeint(f_np, y0, xn)

# 画场线图
fig, ax = plt.subplots(1, 1, figsize=(4, 4))
plot_direction_field(x, y(x), f, ax=ax)
ax.plot(xn, yn, 'b', lw=2)
ax.plot(xp, yp, 'r', lw=2)
plt.show()

 

 

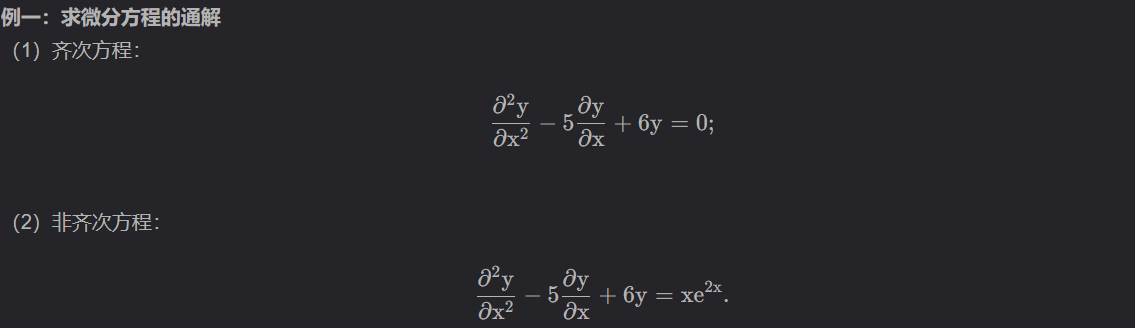
from sympy import *
x = symbols("x")
y = symbols("y",cls=Function)
eq1 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)
eq2 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)-x*exp(2*x)
res = dsolve(eq1,y(x))
res2 = dsolve(eq2, y(x))
print(res)
print(res2)

Eq(y(x), (C1 + C2*exp(x))*exp(2*x))
Eq(y(x), (C1 + C2*exp(x) - x**2/2 - x)*exp(2*x))

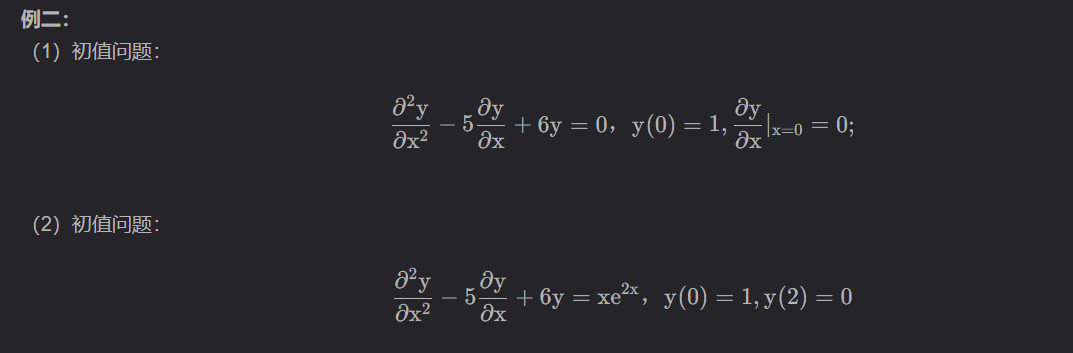
from sympy import *
x = symbols("x")
y = symbols("y",cls=Function)


eq1 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)
eq2 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)-x*exp(2*x)

res1 = dsolve(eq1,y(x),ics={y(0):1,diff(y(x),x).subs(x,0):0})
res2 = dsolve(eq2,y(x),ics={y(0):1,y(2):0})
print(res1)
print(res2)

Eq(y(x), (3 - 2*exp(x))*exp(2*x))
Eq(y(x), (-x**2/2 - x + 3*exp(x)/(-1 + exp(2)) + (-4 + exp(2))/(-1 + exp(2)))*exp(2*x))