KMP复习 + AC自动机
前言
因为学AC自动机,所以来复习trie树和KMP
看到了一篇讲的很好的文章,就一时兴起,写写KMP咯
KMP部分
前置芝士

求解问题
-
在一个文本串S中查找一个模式串t的出现位置
-
也可以引申为求t在s中的出现次数
暴力解法
-
每次i回溯到之前匹配的开头后一位,会导致许多次不必要的重复的匹配,所以有一个很尴尬的时间复杂度,极其不推荐,当然除了你啥也不会了,能拿分就尽量拿吧

KMP数组介绍
-
next[i] : 代表当前字符下标以前的字符串中,前缀和后缀相同的最长长度;
-
next 数组相当于告诉我们:当模式串中的某个字符跟文本串中的某个字符匹配失配时,模式串下一步应该跳到哪个位置。避免像暴力一样尴尬地瞎pp
eg : ABCDAB
从0作为下标开始
next[6] = 2代表下标为0 ~ 5中最长的
相等的前后缀长度为2(就是AB);
-
next求法
首先,蓝书上有对于next[i - 1]的“候选项”为next[i - 1] + 1 或者 next[next[i - 1]]等等有着详细的介绍和解释,我就不多说了(才不是因为我懒)
因为我从0开始存字符,所以我的j又是长度又是下一个该匹配字符的下标
eg : ABACKWABAD
next[8] = 2(即是AB)
同时对于next[9]也该从下标为2的A处继续匹配,并继承next[8]
如果失配了,就一直去找更次的“候选项”,就是next[next[i - 1]]等等
跳出之后判一下下一位(下标就是j所以不用加1)可不可以计入
对于结束的while循环,或者匹配成功,或者j = 0
1. 如果匹配成功,则有s[i] == s[j],nxt[i] = j + 1
2. 如果j = 0, 则有 nxt[i] = (s[i] == s[j])
void get_nxt(const char s[]) {
int len = strlen(s);
nxt [0] = 0;
for(int i = 1; i < len; i ++) {
//下标从0开始, 那么j既是真前后缀的长度,也是下一个该匹配的字符的下标,多循环了一位,从1开始
int j = nxt[i - 1];
while(j > 0 && s[i] != s[j]) {j = nxt[j - 1];}//不配,去找次长
if(s[i] == s[j]) ++j;
nxt[i] = j;//j = 0 | j = 1 | j = k + 1
}
}
- 也给出一个从1开始存的
void get_nxt(const char s[]) {
int len = strlen(s + 1);
nxt[1] = 0;
for(int i = 2, j = 0; i <= len; i ++) {
while(j && s[i] != s[j + 1])j = nxt[j];
if(s[i] == s[j + 1])nxt[i] = ++j;
else nxt[i] = 0;
}
}
KMP进行中
- 分别给出从1和从0开始存的代码,可以自己看一下下标的区别
code展示
- 出现次数,从0开始存
int num_match(char s[], char t[]) { //text串和s串
int n = strlen(s);
int m = strlen(t);
for(int i = 0, j = 0; i < m; i ++) {
while(j > 0 && t[i] != s[j]) j = nxt[j - 1];
if(t[i] == s[j])++j;
if(j == n) {
++ans;
j = nxt[j - 1];
}
}
return ans;
}
- 有没有出现过(从1开始存)
int match(char s[], char t[]) {
int m = strlen(s + 1);
int n = strlen(t + 1);
for (int i = 1, j = 0; i <= n; ++i) {
while (j && t[i] != s[j + 1]) j = next[j];
if (t[i] == s[j + 1]) ++j;
if (j == m) return i - j + 1;
}
}
-
代码解释
对于(j == n)是判断有没有重叠的部分
其他的跟暴力没啥区别,就是加了个next的挂,然后他就起飞了,哎,有挂的算法就是强
AC自动机部分、
没错,它不仅不能让你AC还能让你自动WA
概念明析
- 自动机 : 一个自动机M ,若它能识别(接受)字符串 ,那么M(S) = True,否则M(s) =
False 。(比如有Trie树,回文自动机,后缀自动机,子序列自动机,KMP自动机(除了Trie树全不会咋整)) - AC(其实它是人名...) : 当一个自动机读入一个字符串时,从根节点起按照转移函数一个一个字符
地转移。如果读入完一个字符串的所有字符后处于一个接受状态(可以被匹配),那么我们称这个自动
机接受(AC)这个字符串,否则称这个自动机 不接受这个字符串。 - 它是AC自动机,不是自动AC机!
原理
- 以Trie的结构为基础 ,结合KMP的思想
步骤
- 将所有的模式串构成一棵Trie
- 对Trie树上所有的结点构造失配指针
求解问题
- 进行多模式匹配,一个S串跟一坨t串匹配(毕竟一个一个KMP那不就\(n^{2}\)
过百万了)
各种解释
-
最初建起的Trie树就是最普通的Trie树,你之前怎么写现在就怎么写就行
-
对于Trie的结点含义 : 表示某个模式串的前缀,也可以叫做状态,一个不同的节点表示不同的状态,Trie的边就是状态的转移
-
失配指针fail :
-
与next的对比
- 共同点 : 两者同样是在失配的时候用于跳转的指针。
- 不同点 : KMP要求的是前后缀相等的最长,而AC自动机只需要相同后缀即可。
(因为KMP只对一个模式串做匹配,而AC自动机要对多个模式串做匹配) - 有可能fail 指针指向的结点对应着另一个模式串,两者前缀不同。也就是说,AC自动机在对匹配串做逐位匹配时,同一位上可能匹配多个模式串。因此fail指针会在字典树上的结点来回穿梭,而不像KMP在线性结构上跳转。
-
对于fail的理解
- fail[i]为与以i节点为结尾的串的后缀有最大公共长度的前缀的结尾编号
-
-
num指以当前子母为末尾的单词个数
Code时间
- 建树,就是普普通通的Trie树
struct Trie {
int fail;//失配
int num;//有几个字串以当前字母作为结尾
int ch[28];//子节点位置
}tr[maxn];//tri树
fuc(void, build) (string s) {
int len = s.length();
int now = 0;
for (Re i = 0; i < len; i++) {//没有当前节点
int tmp = s[i] - 'a';
if (tr[now].ch[tmp] == 0)tr[now].ch[tmp] = ++cnt;//存一下节点
now = tr[now].ch[tmp];//向下建树
}
tr[now].num++;//一个单词存完
}
-
构建fail数组
- 先放代码
fuc(void, get_fail)() {
queue<int> q;//bfs处理fail
//因为fail是看已经处理好的,所以我在处理当前层的fail时,上面层的必须都处理好
for (Re i = 0; i < 26; i++) {
if (tr[0].ch[i] != 0) {
tr[tr[0].ch[i]].fail = 0;//指向根
q.push(tr[0].ch[i]);
}
}
while (!q.empty()) {
int top = q.front();
q.pop();
for (Re i = 0; i < 26; i++) {
if (tr[top].ch[i] != 0) {//存在当前点
tr[tr[top].ch[i]].fail = tr[tr[top].fail].ch[i];
//子节点的fail指针指向当前节点的fail指针所指向的节点的相同子节点
q.push(tr[top].ch[i]);
}
else {
tr[top].ch[i] = tr[tr[top].fail].ch[i];
//当前节点的这个子节点指向当前节点fail指针的这个子节点
//因为我没有这个儿子,所以我去找我fail可能我fail也没有
//我fail直接指向了fail的fail所以最终指向有这个儿子的或者直接指回根
//可以理解为路径压缩或者换链
}
}
}
}
-
开始解释
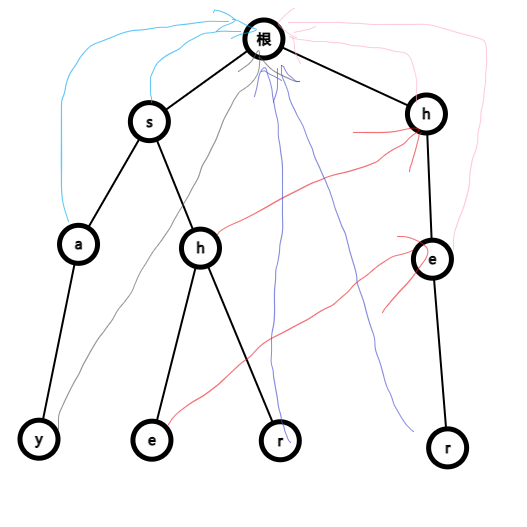
- fail指的是最长的能和 另外一个串 前缀匹配的后缀,所以如果一个点a有一个儿子点t, 那么t的fail实际上就是a的fail的t儿子(假如a和a的fail都有t这个儿子)
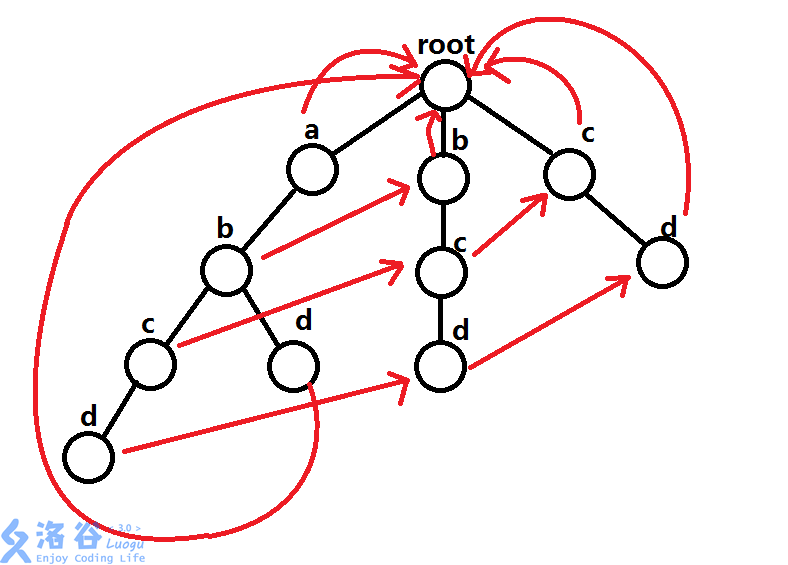
-
(
借用luogu上一个大佬的tu,跟ta申请了)- 在这样一个树上去匹配abcde,找到d之后发现没有e,然后就可以一直套娃下去了
话说我代码里写的不比这里详细吗
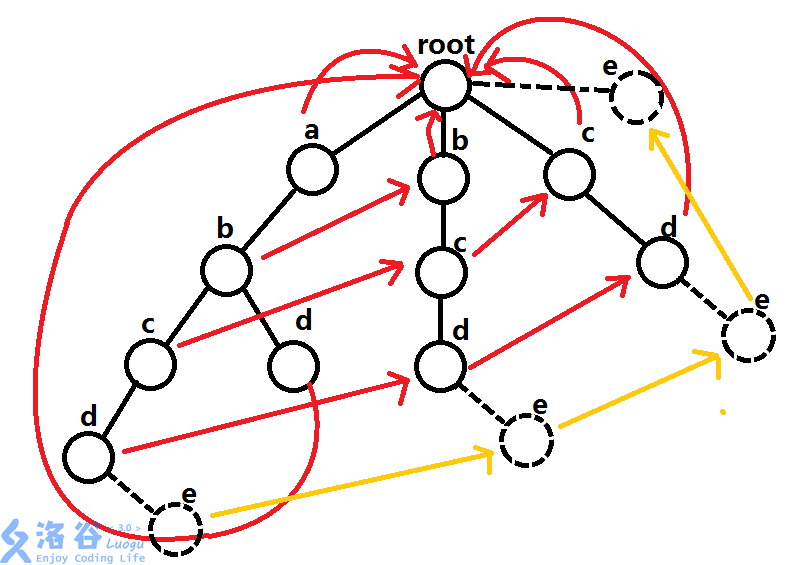
- 在这样一个树上去匹配abcde,找到d之后发现没有e,然后就可以一直套娃下去了
-
- fail指的是最长的能和 另外一个串 前缀匹配的后缀,所以如果一个点a有一个儿子点t, 那么t的fail实际上就是a的fail的t儿子(假如a和a的fail都有t这个儿子)
-
query
-这里以LuoguP3808为例
-这个代码挺好理解的吧,就不解释了
fuc(int, query)(string s) {
int len = s.length();
int now = 0, ans = 0;
for (Re i = 0; i < len; i++) {
now = tr[now].ch[s[i] - 'a'];
for (Re tmp = now; tmp && tr[tmp].num != -1; tmp = tr[tmp].fail) {
ans += tr[tmp].num;
tr[tmp].num = -1;
}
}
return ans;
}
- 说一个我理解时的误区
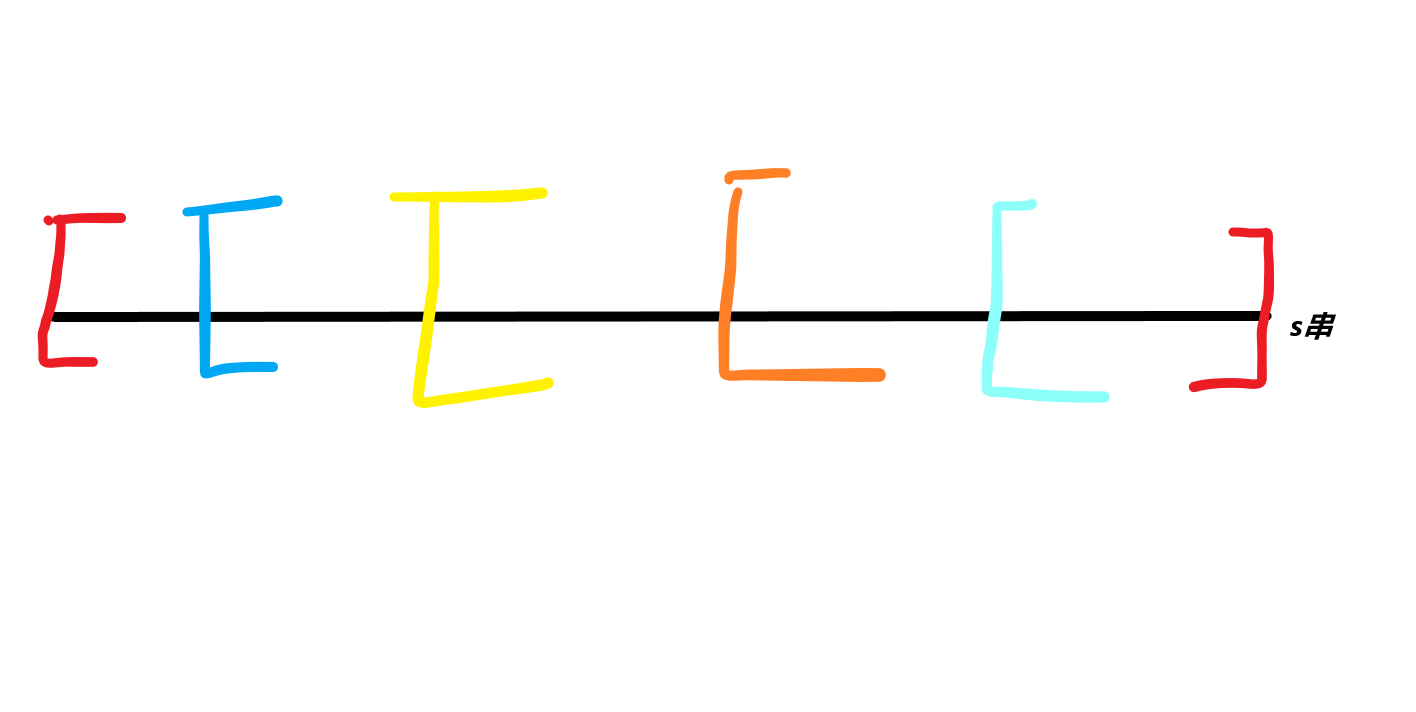
- 我先去匹配红色的,当红色的失配之后我是去匹配蓝色(跳fail跳到最大后缀)的,此时相当于我已经换串了,是蓝色到红色的串而非红色到红色的串,所以AC自动机能做到很快匹配一坨,因为他同时处理...虽然可能很傻逼,但是确实是我当时没理解的。

 KMP复习 + AC自动机
KMP复习 + AC自动机

 浙公网安备 33010602011771号
浙公网安备 33010602011771号