HAOI2007覆盖问题

这个题吧，什么叫思路啊

可能这个思路已经有人写过了，但还是加一点自己的理解吧
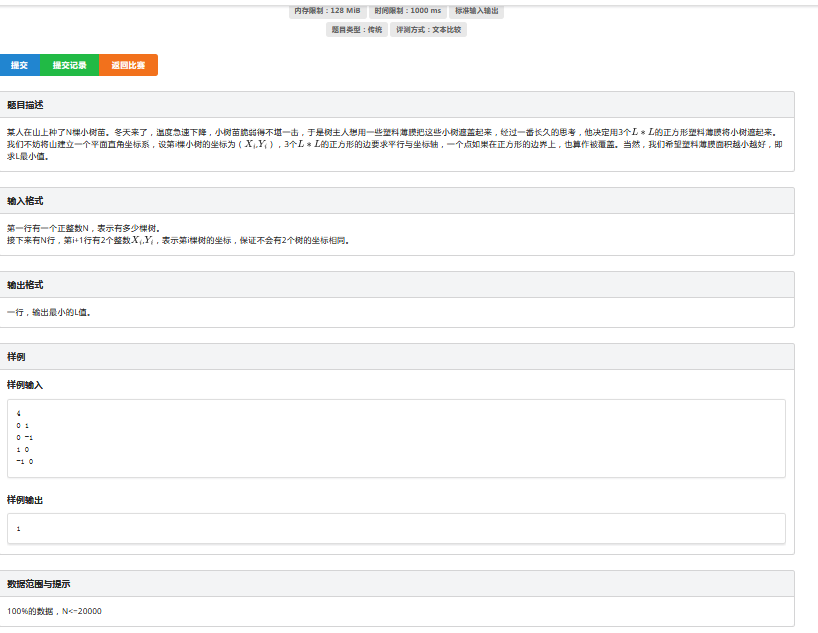
首先去将所有点的极差（左右，上下）求出来构造一个初始的矩形，能够覆盖所有的点，又因为要放三个正方形，那么必须要有一个正方形在矩形的四个角，那么之后我们只需要枚举第一个正方形在四个角之后，再去放另外两个正方形
那么我们在考虑用两个正方形去填满一个新的大矩形（用没被第一个正方形覆盖的点去构造，还是极差），手模之后会发现只有两种情况，一个在左上，一个在右下，或者一个在右上，一个在左下
假设是 一个在左上一个在右下
我们能知道在左上的正方形一定要盖住横坐标最左的
和纵坐标最上的点 　
同理，那么处于右下方的正方形也同样
于是，我们可以愉快地开始coding了

点击查看代码

#include <bits/stdc++.h>
using namespace std;
	

namespace kiritokazuto {
	template <typename T> inline void in(T &x) {
		int f = 0; x = 0; char c = getchar();
		while(c < '0' || c > '9')f |= c == '-', c = getchar();
		while(c >= '0' && c <= '9')x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
		x = f ? -x : x;
	}
	template <typename T> inline void ot(T x) {
		if(x < 0)putchar('-'), x = -x;
		if(x > 9)ot(x / 10);putchar(x % 10 | '0');
	}
}

using namespace kiritokazuto;

namespace work {
	#define Re register int
	#define ki kiritokazuto
	#define LL long long 
	static const int maxn = 1e4 + 10, Inf = 2147483647;
	struct WMX{
		int x, y;
	}a[maxn];
	int n, m, L, R;
	int cobe[maxn];
	int num = 0;
	inline bool cover(int len) {
		if(!num)return true;
		Re i;
		int l, r, up, down;
		l = down = Inf;
		r = up = -Inf;
		for(i = 1; i <= num; i++) {
			l = min(l, a[cobe[i]].x);
			r = max(r, a[cobe[i]].x);
			up = max(up, a[cobe[i]].y);
			down = min(down, a[cobe[i]].y);
		}
	    /*一个角建好，枚举剩余两个正方形 
	    枚举这两个正方形放在哪里，才能尽量覆盖全部点
　　    一种是一个在左上一个在右下
        另外一种是 一个在右上一个在左下。
		*/
		for(i = 1; i <= num; i ++) {
			if(!(a[cobe[i]].x <= l + len && a[cobe[i]].y <= down + len ||
				 a[cobe[i]].x >= r - len && a[cobe[i]].y >= up - len) )break;
		}
		if(i > num)return true;//没有跳出i = num + 1全覆盖，true
		for(i = 1; i <= num; i ++) {
			if(!(a[cobe[i]].x <= l + len && a[cobe[i]].y >= up - len ||
				 a[cobe[i]].x >= r - len && a[cobe[i]].y <= down + len) )break;
		}
		if(i > num)return true;
		else return false;
	}

	
	inline void creat(int l, int r, int down, int up){
		Re i;//此处不可将Re放进去，否则会重新定义一个局部的num，而非全局 
		for(i = 1, num = 0; i <= n; i ++) {
			if(a[i].x < l || a[i].x > r || a[i].y < down || a[i].y > up) {
				cobe[++num] = i;
			}
		}
	}


	inline void kirito() {
		in(n);
		int l, r, up, down;
		l = down = Inf;
		r = up = -Inf;
		for(int i = 1; i <= n; i ++) {
			in(a[i].x);
			in(a[i].y);
			l = min(l, a[i].x);
			r = max(r, a[i].x);
			up = max(up, a[i].y);
			down = min(down, a[i].y);
		}
		L = 0;
		R = max(up - down, r - l);//先构造出能覆盖所有点的矩形
		Re i;
		while(L < R) { 
			int mid = (L + R) / 2;
			for(i = 1; i <= 4; i++) {//枚举四个角 
				if(i == 1)creat(l, l + mid, down, down + mid);
				else if(i == 2)creat(l, l + mid, up - mid, up);
				else if(i == 3)creat(r - mid, r, down, down + mid);
				else if(i == 4)creat(r - mid, r, up - mid, up);
				if(cover(mid))break;
			}
			if(i <= 4) R = mid;//终止条件没有等于 
			else L = mid + 1;//四个角都不行，加长
			//如果for执行完i = 5; 
		}
		ot(L);
	
	}
}

signed main() {
	work :: kirito();
}