DS复习

Exam

第一章绪论：基本概念和术语/程序时间复杂度计算

数据/数据元素/数据字段/数据项/数据对象/数据结构DS = {D, S} D为数据对象，S为该对象中所有数据成员之间的关系的有限集合

四个基本结构：集合、线性结构、树形结构、网状结构（逻辑结构：线性、非线性/物理结构：顺序、链接、索引、散列）

抽象数据类型ADT：数据结构+定义在此数据结构上的一组操作 = {D, S, P}

算法分析：有穷性/确定性/可行性/输入/输出 算法性能标准：正确性/可读性/效率/健壮性

时间复杂度：算法中语句重复执行次数的数量级\(T(n) = O(f(n))\)

空间复杂度：变量/递归栈/new、delete

第二章线性表：线性表、顺序表、链表的基本操作/循环链表、双向循环链表基本操作

线性表(逻辑结构)：n个数据元素的有限序列

顺序表(物理结构)：线性表的顺序存储表示(数组存储)——插入、删除、查找

链表(物理结构Node:data|link)：线性表的链接存储表示(单链表/静态链表/循环链表/双向循环链表)——插入(前/后插法建立单链表)、删除、单链表清空、查找

静态链表：用一维数组描述线性链表

循环链表：最后一个结点指向头结点

双向循环链表：Node:prior|data|link

第三章栈和队列：栈的定义、特点；顺序栈和链式栈/队列的定义、特点；链队列；循环队列/递归：定义是递归的、 数据结构是递归的、问题的解法是递归的

栈：仅在表尾进行插入或删除操作的线性表(top栈顶)(LIFO)——进栈、出栈、取栈顶

顺序栈：top指针在最后一个元素的下一位置

链式栈：top为头结点，指向栈顶元素

进制转换/行编辑程序(#退格#退行)/迷宫求解/表达式求值(前/中/后缀，需要2个栈)

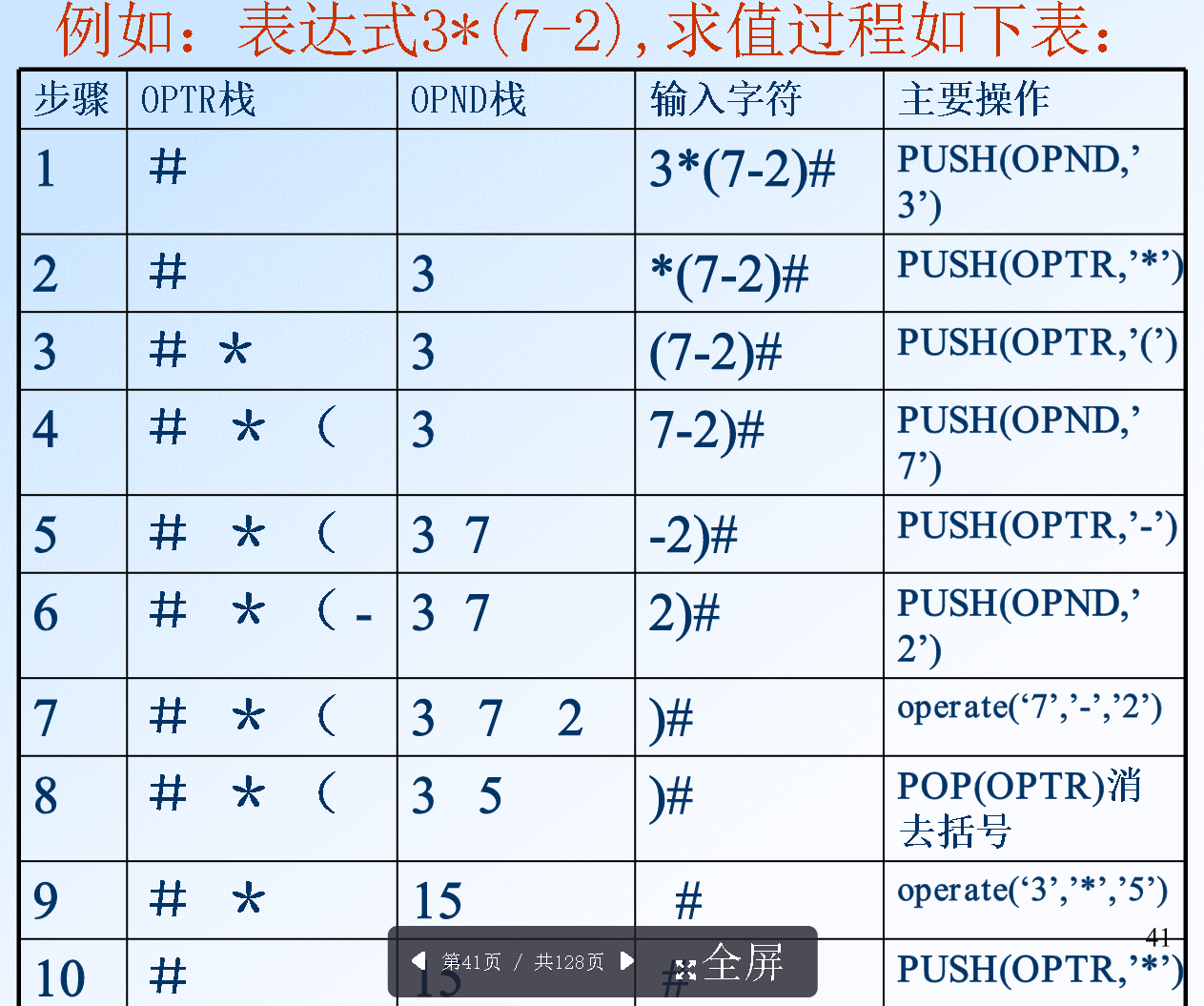
队列：在表一段插入，另一端删除(rear队尾、front队头)(FIFO)——入队、出队、取队头

链队列：Node：data|next 有front、rear指针

循环队列：数组存储，环状空间。头指针指向队头，尾指针指向队尾的下一个位置(入队：Q->rear = (Q->rear+1)%MAXSIZE出队：Q->front = (Q->front+1)%MAXSIZE)

优先队列：优先级最高的出队，堆实现

杨辉三角

定义是递归的：阶乘函数、斐波那契数列

数据结构是递归的：单链表的遍历操作

问题的解法是递归的：汉诺塔

非递归化：用栈保存中间结果(图章节中，非递归DFS)

第六章树和二叉树：*二叉树的定义、性质、二叉树的构建/二叉树遍历及算法；二叉树应用/*二叉树计数，树和森林与二叉树间的转换/哈夫曼树的构建，哈夫曼编码

根结点、结点、叶结点、结点的度、子女、兄弟、祖先、子孙、结点层次、树的深度、树的高度、有序树、森林

二叉树：每个结点至多只有两棵子树(不存在度大于2的结点)

满二叉树、完全二叉树 顺序表示、链表表示Node:lchild|data|rchild/lchild|data|parent|rchild

二叉树遍历：前/中/后序 递归/非递归(栈)

递归计算二叉树结点个数/叶子结点个数/高度//复制二叉树/判断二叉树等价/交换左右子树

？线索二叉树：Node:lchild|lthread|data|rthread|rchild
lthread = 0->lchild为左子女指针
lthread = 1->lchild为前驱线索
rthread = 0->rchild为右子女指针
rthread = 1->rchild为后继线索

*二叉树计数：由前序、中序表示可唯一确定一棵二叉树

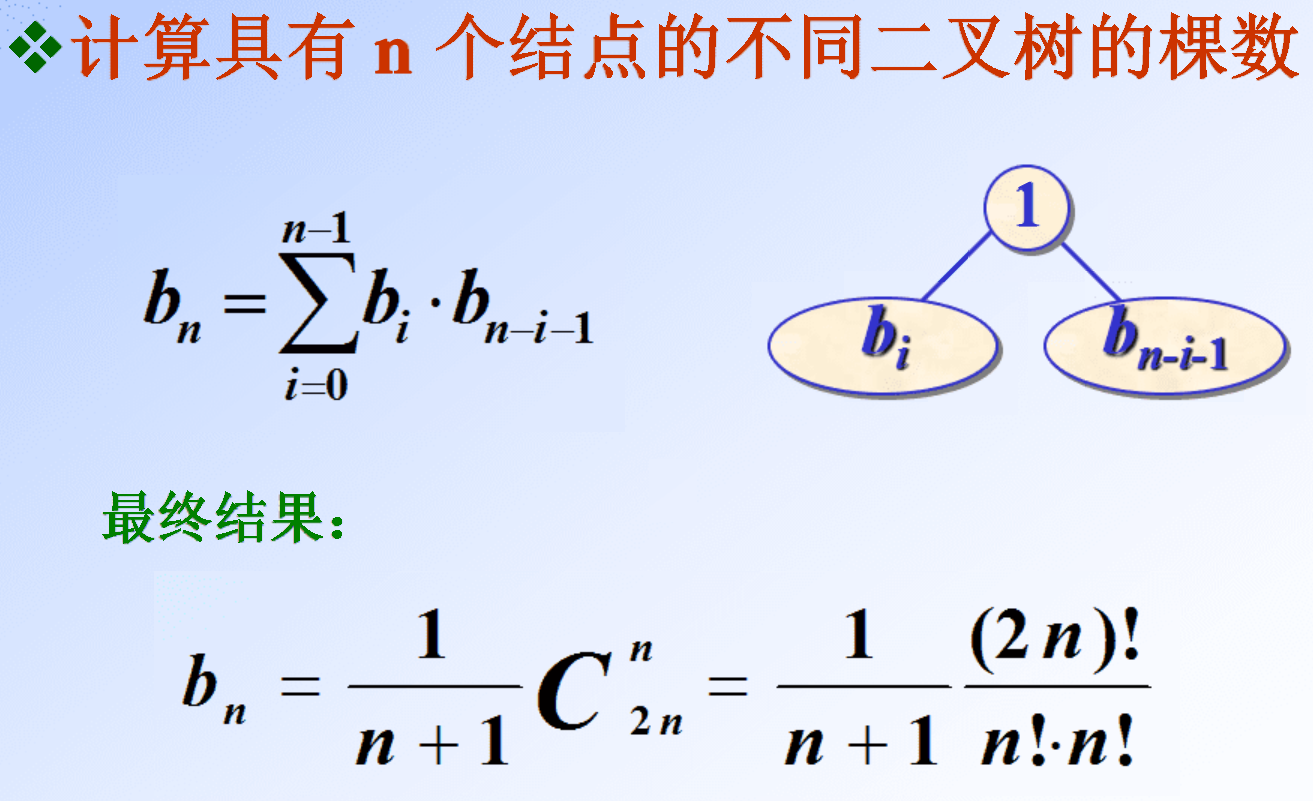
*森林与二叉树的转换：父子变成左子树、兄弟变成右子树

路径长度(Path Length, PL) = EPL(叶节点到根结点的路径长度之和) + IPL(内结点到根结点的路径长度之和)

带权路径长度(WPL)：路径长度乘权重之和

哈夫曼树：带权路径长度最小的二叉树(权值大的结点离根最近)

如何构造？权值最小的两个叶节点为兄弟，递归构造

哈夫曼编码：按各个字符出现的概率不同，赋予不等长的编码。

如何求？以概率为权值，建立哈夫曼树，左分支赋予0，右分支赋予1

第七章图:图的基本概念/*图的定义、图的存储结构/*图的遍历（广度优先遍历、深度优先遍历）/*拓扑排序、利用Prim算法构造最小生成树的实现过程、基于Dijkstra算法的最短路径实现过程、关键路径实现过程

图：顶点集合+顶点间的关系集合 G = (V, E)

无向图\(E = \{(v, w)|v, w \in V\}\)

有向图\(E = \{<v, w>|v, w \in V\}\)

完全图、稀疏图/稠密图、带权图、子图、连通图与连通分量/强连通图与强连通分量、

邻接结点、度/入度/出度TD = ID + OD、路径、简单路径、简单回路、路径长度

生成树：假设一个连通图有 n 个顶点和 e 条边，其中 n-1 条边和 n 个顶点构成一个极小连通子图，称该极小连通子图为此连通图的生成树。

对非(强)连通图，则称由各个连通分量的生成树的集合为此非(强)连通图的生成森林。

*图的存储结构：邻接矩阵、邻接表 带权？

*图的遍历：DFS/BFS(可求连通分量)从图中某一顶点出发访遍图中所有的顶点，且使每个顶点仅被访问一次 辅助数组visited[]

*DFS(递归/栈，O(n+e)/O(n^2))：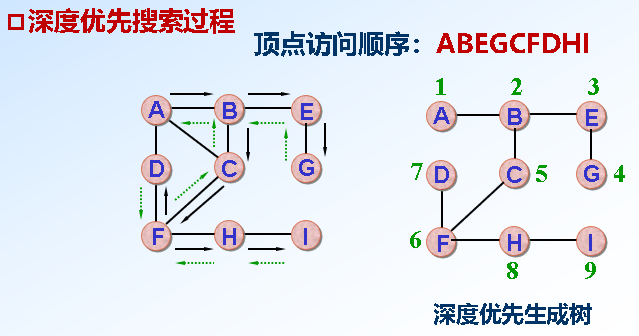

*BFS(队列，O(n+e)/O(n^2))：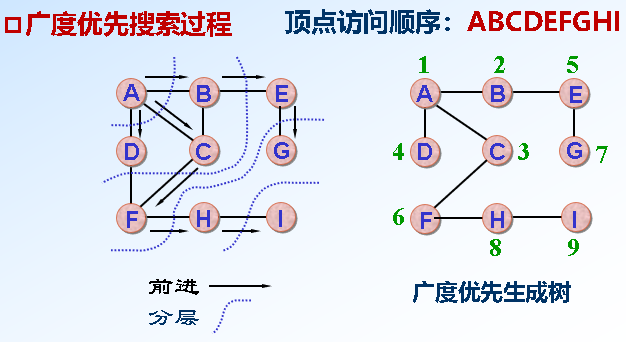

*Prim算法：贪心，遍历点，O(n^2)，适用于边稠密，邻接矩阵

*拓扑排序(AOV网络，判断有向图是否有环，邻接表，入度为零的栈)：

*关键路径(AOE网络，顺拓扑、逆拓扑)：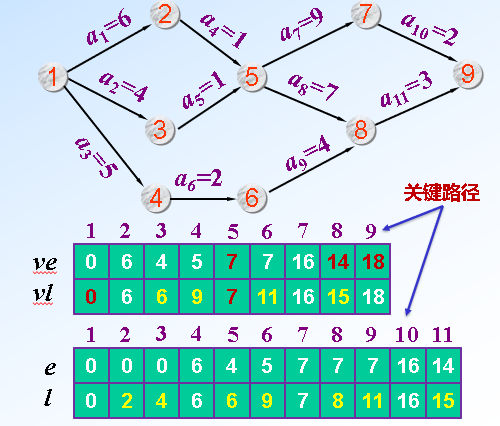

*Dijkstra算法(无负权单源最短路径)：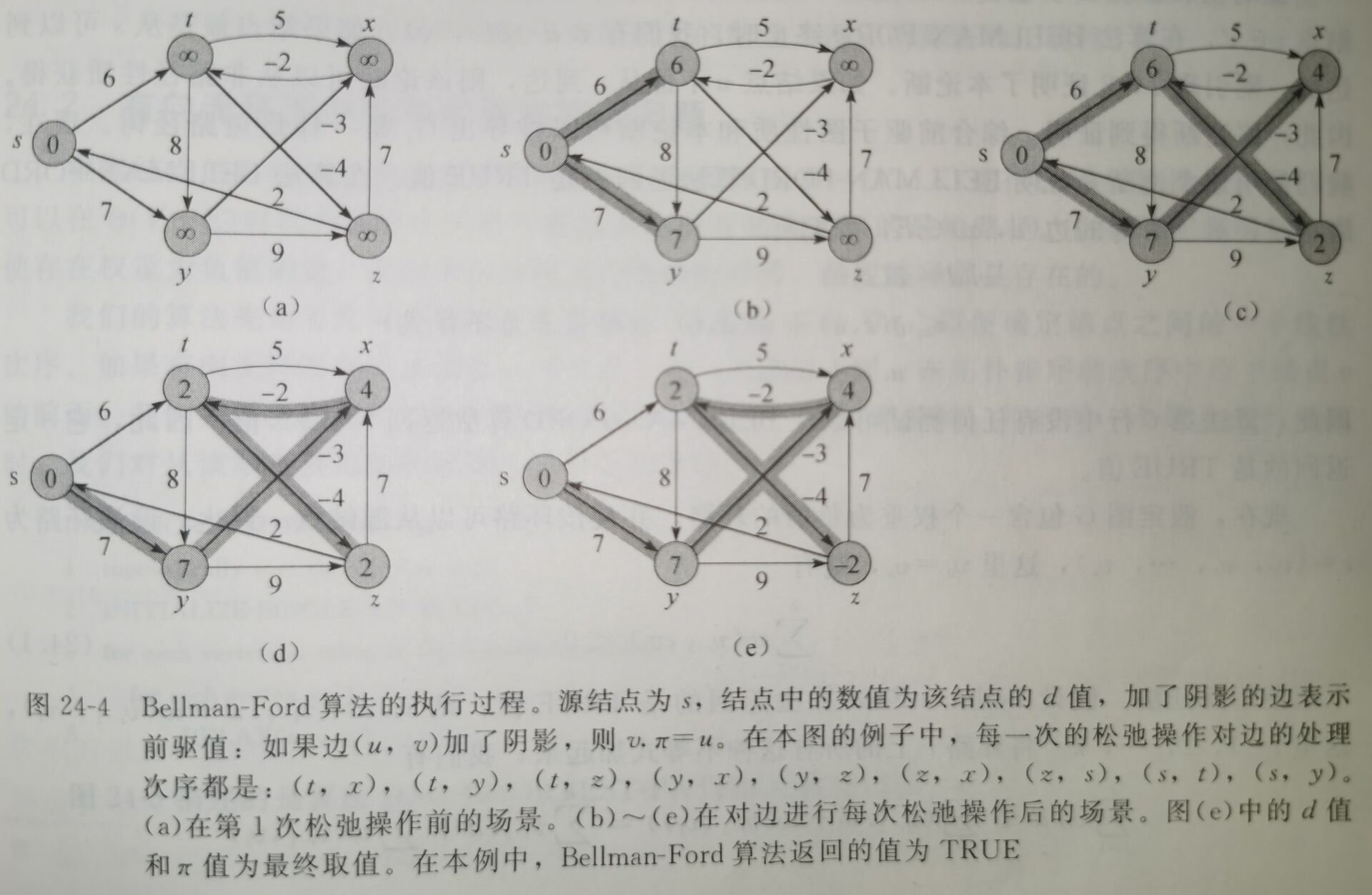

第八章查找：查找的分类、折半查找的算法以及实现过程/*二叉平衡树构建过程/*B-树和B+树操作/*哈希表的构建过程，用除留余数法解决冲突

有序表的折半查找O(logn)：每次将待查记录所在区间缩小一半(begin+end越界？)

*AVL树(单旋转、双旋转)：树中每个结点的左、右子树深度之差的绝对值不大于1

*B树：一种平衡的多路查找树(point value:m/2取上界)

查找：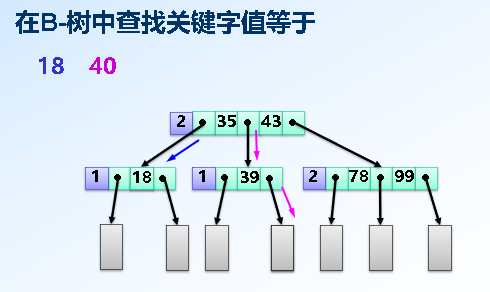

插入：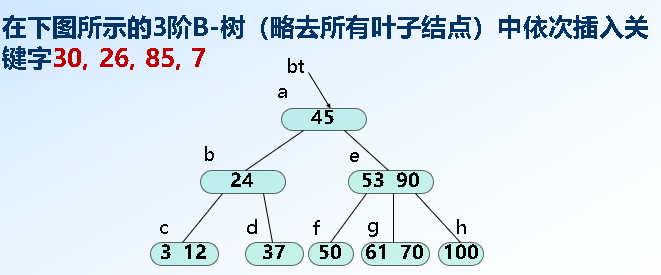

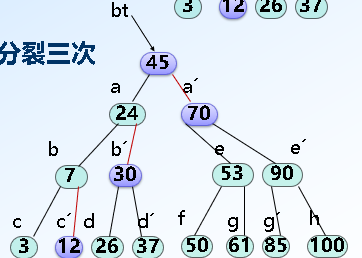
删除：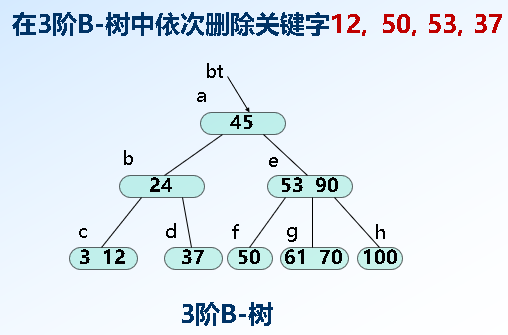

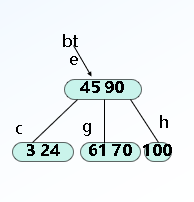
*B+树：区别：关键字个数和子树个数一样多、所有叶子结点中包含全部关键字信息、所有非终端结点可看成索引，结点中仅含有其子树中的最大（或最小）关键字

查找：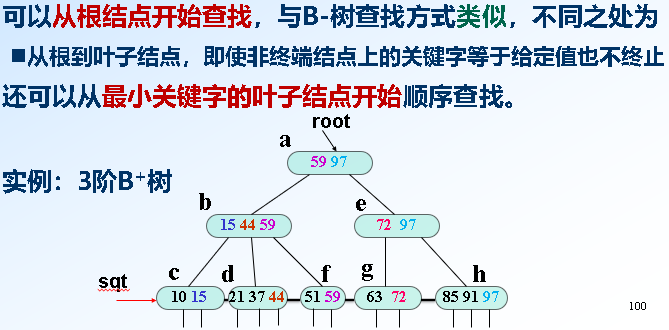

*哈希表：映射

除留余数法：

处理冲突：为产生冲突的地址寻找下一个哈希地址

第九章内排序:内排序的分类/直接插入排序实现过程/直接选择排序实现过程/起泡排序实现过程/*快速排序及一趟排序实现过程/*大顶堆和小顶堆构建过程及堆排序的实现过程

内排序的分类：按方法/按时间复杂度

直接插入排序(稳定)：

希尔排序(不稳定)：先将整个待排记录序列分割成为若干子序列分别进行直接插入排序|待整个序列中的记录基本有序时，再对全体记录进行一次直接插入排序(取gap递减，分组插入排序)

冒泡排序(稳定)：n-1趟排序，依次排出最大数放在n-i处

*快速排序(不稳定，可递归，O(nlogn))：选基准pivot，小于防左边，大于等于放右边

直接选择排序(不稳定)：n-1趟排序，依次选择最小的放在i处

堆：是一棵完全二叉树/每个节点的值都大于或等于其子节点的值，为大顶堆；反之为小顶堆

大顶堆和小顶堆构建过程：将无序序列看成完全二叉树，从最后一个元素开始自下向上逐步调整为小顶堆/大顶堆

堆排序的实现过程(不稳定，O(nlogn))：建立大顶堆，输出根结点，并与最后一个元素交换，剩下结点重新建立大顶堆，直到所有结点都排序完成

归并排序(稳定，O(nlogn))：分而治之

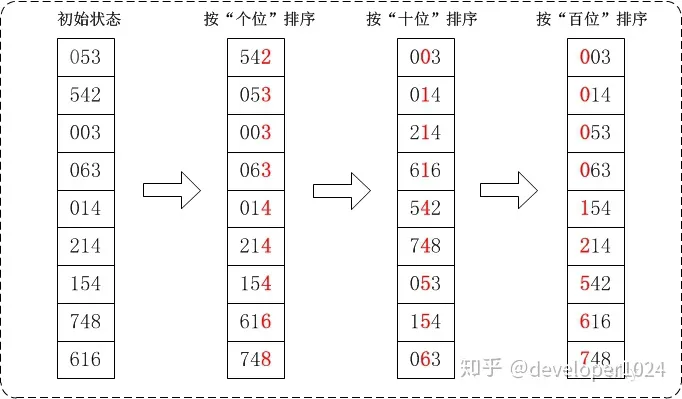
基数排序：将整数按位数切割成不同的数字，然后按每个位数分别比较。MSD(最高位优先法)：先从高位开始进行排序，在每个关键字上，可采用计数排序；LSD(最低位优先法)：先从低位开始进行排序，在每个关键字上，可采用桶排序