数据结构与算法分析——C语言描述（第4章树）

4.1 预备知识
- 4.1.1 树的实现
- 4.1.2 树的遍历及应用
4.2 二叉树(binary tree)
- 4.2.1 实现
- 4.2.2 表达式树(expression tree)
  - 构造一棵表达式树
4.3 查找树ADT——二叉查找树
- 平均情形分析
4.4 AVL树
4.5 伸展树(splay tree)
- 4.5.1 一个简单的想法
- 4.5.2 展开(splaying)
4.6 树的遍历
4.7 B树(B-tree)

4.1 预备知识

一棵树(tree)是一些节点的集合。这个集合可以是空集；若非空，则一棵树由称作根(root)的节点\(r\)以及0个或多个非空的（子）树\(T_1\), …, \(T_k\)组成，这些子树中每一棵的根都被来自根\(r\)的一条有向的边(edge)所连接。
从递归的定义中可以发现，一棵树是\(N\)个节点和\(N-1\)条边的集合。

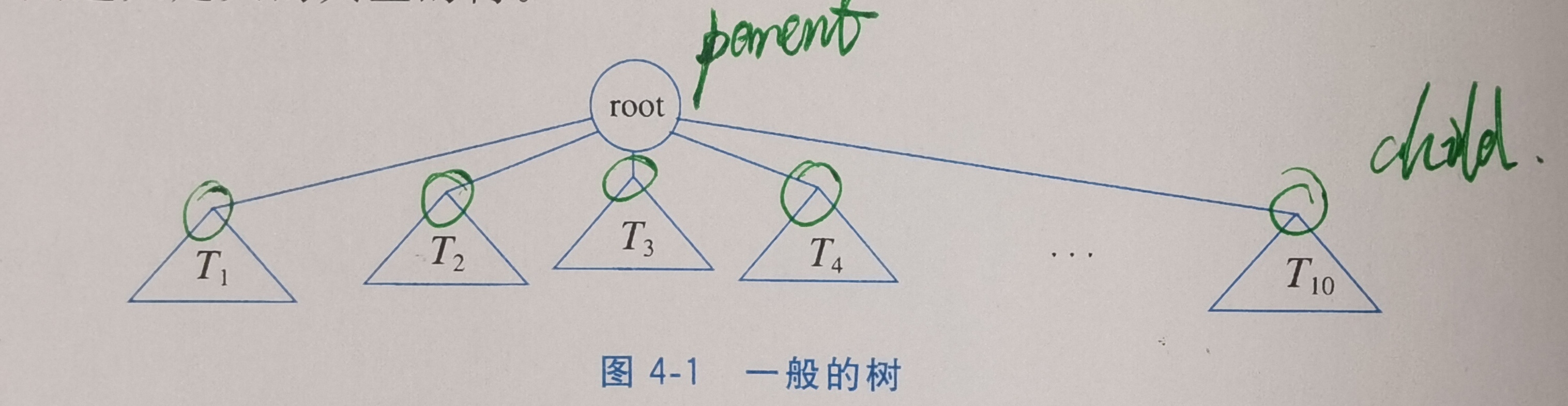
每一棵子树的根叫作根\(r\)的儿子(child)，而\(r\)是每一棵子树的根的父亲(parent)。（同理有祖父(grandparent)和孙子(grandchild)关系）
没有儿子的节点称为树叶(leaf)。
具有相同父亲的节点称为兄弟(sibling)。
节点到节点的路径(path)定义为途径节点的一个序列，这个路径的长(length)为该路径上面的边的条数。
节点的深度(depth)定义为从根到节点的唯一路径的长。（根的深度为0）
节点的高(height)定义为节点到一片树叶的最长路径的长。
如果存在从\(n_1\)到\(n_2\)的一条路径，那么\(n_1\)是\(n_2\)的一位祖先(ancestor)，而\(n_2\)是\(n_1\)的一个后裔(descendant)。如果\(n_1≠n_2\)，那么\(n_1\)是\(n_2\)的一位真祖先(proper ancestor)，而\(n_2\)是\(n_1\)的一个真后裔(proper descendant)。

4.1.1 树的实现

实现树的一种方法可以是将每个节点的所有儿子都放在树节点的链表中。
树的节点声明：

typedef struct TreeNode *PtrToNode;

struct TreeNode
{
 ElementType Element;
 PtrToNode FirstChild;
 PtrToNode NextSibling;
}

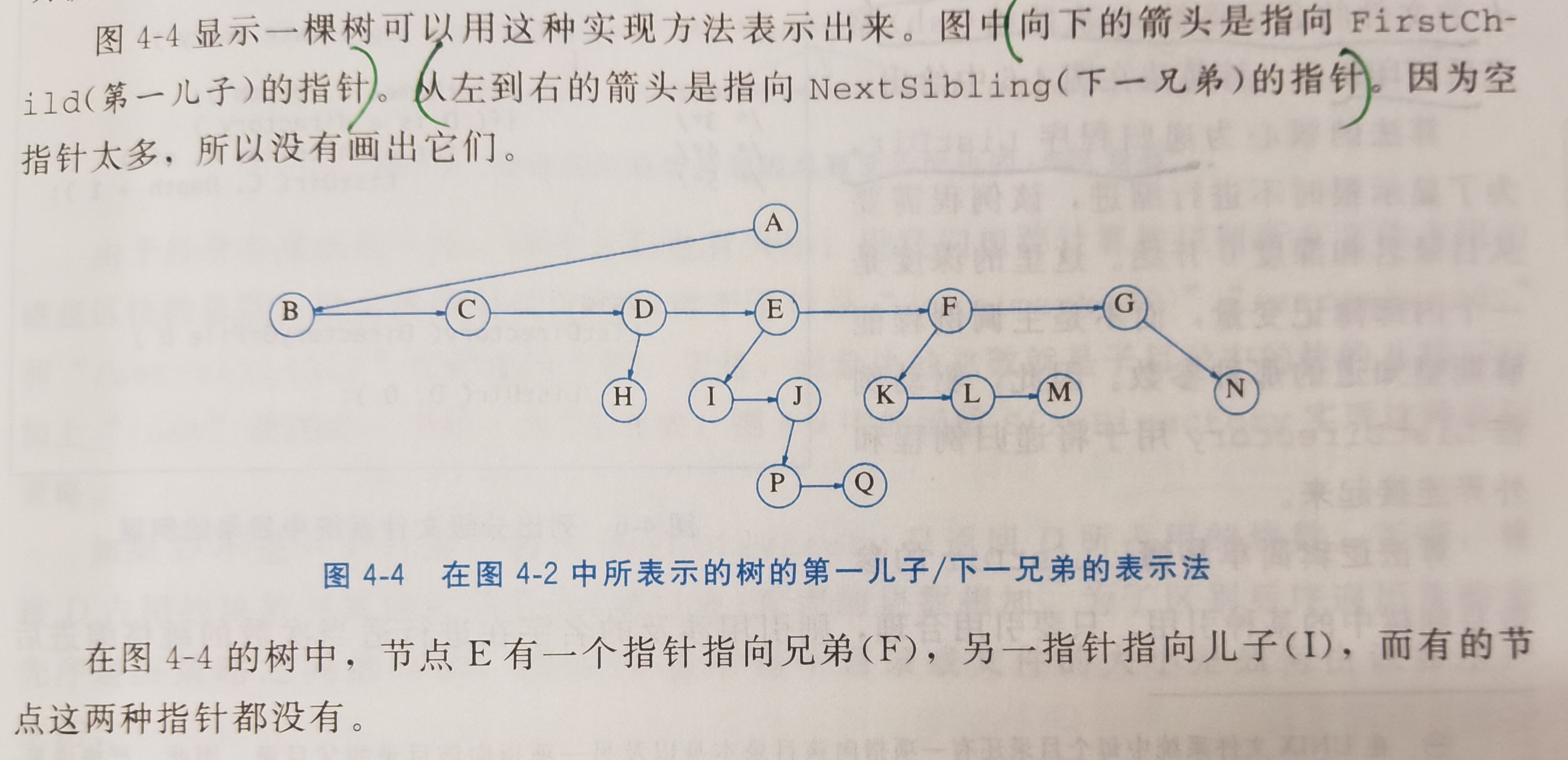
4.1.2 树的遍历及应用

典型应用——常用操作系统的目录结构。

遍历树的策略：

先序遍历(preorder traversal)

后序遍历(postorder traversal)

中序遍历(inorder traversal)

层序遍历(level-order traversal)

具体的遍历方式将在4.6详细介绍。

4.2 二叉树(binary tree)

特征：每个节点的儿子都不能多于两个。
二叉树的一个性质是平均二叉树的深度要比\(N\)小的多，平均深度为\(O(\sqrt{N})\)；对于二叉查找树(binary search tree)，平均深度为\(O(\log{N})\)。（最坏情况下为\(N-1\)）

4.2.1 实现

二叉树节点声明：

typedef struct TreeNode *PtrToNode;
typedef struct PtrToNode Tree;

struct TreeNode
{
 ElementType Element;
 Tree Left;
 Tree Right;
}

特别地，当进行一次插入时，必须调用\(malloc\)创建一个节点。节点可以在调用\(free\)删除后释放。

二叉树实际上就是图(graph)。

二叉树的主要用处之一是在编译器的设计领域。

4.2.2 表达式树(expression tree)

特征：树叶是操作数(operand)，其他的节点为操作符(operator)。

中序遍历：先通过递归产生一个带括号的左表达式，然后打印出在根处的运算符，最后再递归地产生一个带括号的右表达式而得到一个（对两个括号整体进行运算的）中缀表达式(infix expression)。
后序遍历：递归打印出左子树、右子树，然后打印运算符。对于上述例子输出“a b c * + d e * f + g * +”。
先序遍历：先打印出运算符，然后递归地打印出右子树和左子树。对于上述例子输出“+ + a * b c * + * d e f g”。（不太常用的前缀(prefix)记法）

构造一棵表达式树

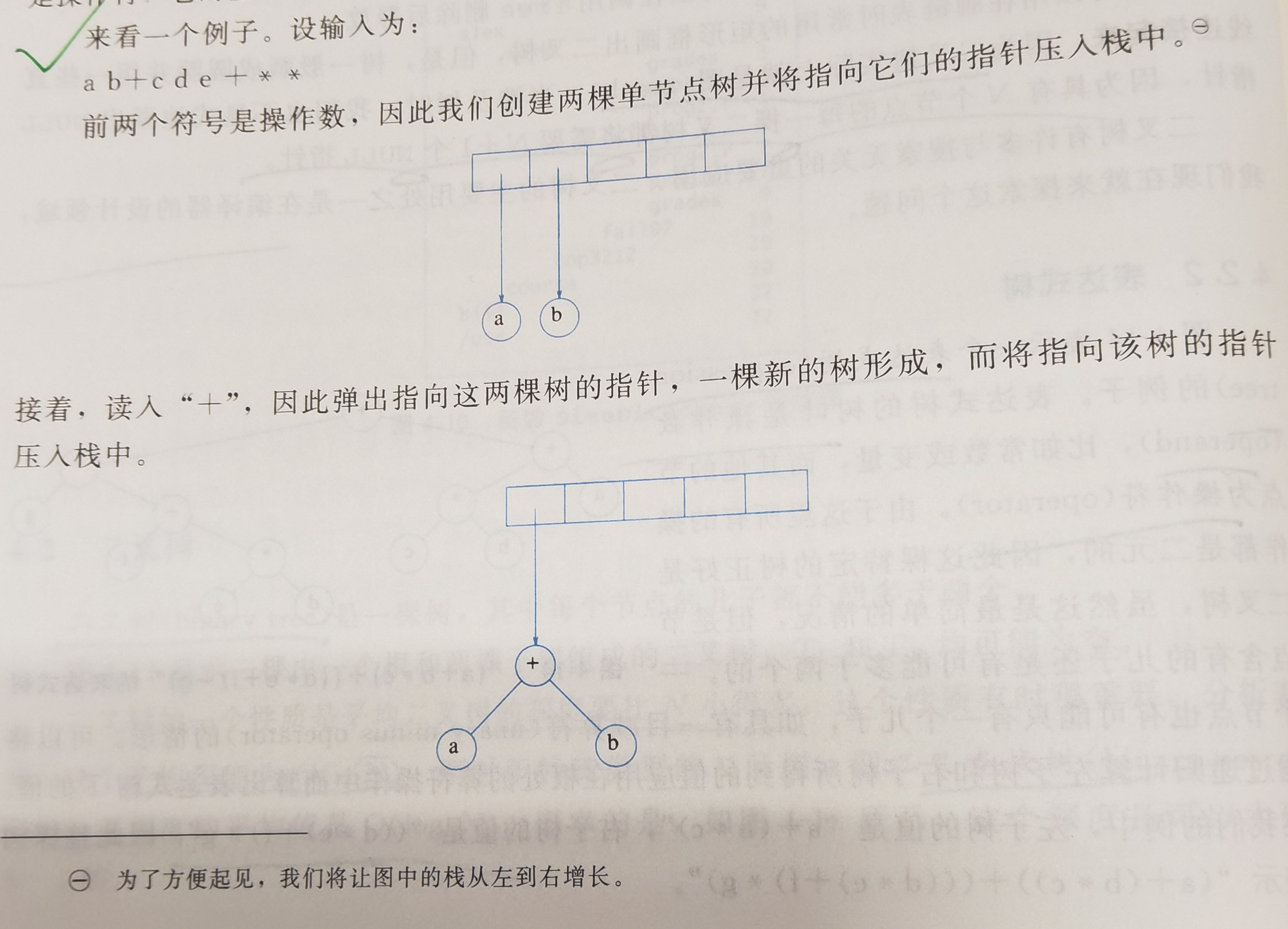
一次一个符号地读入表达式（利用栈）

如果符号是操作数，建立一个单节点树并将一个指向它的指针推入栈中。
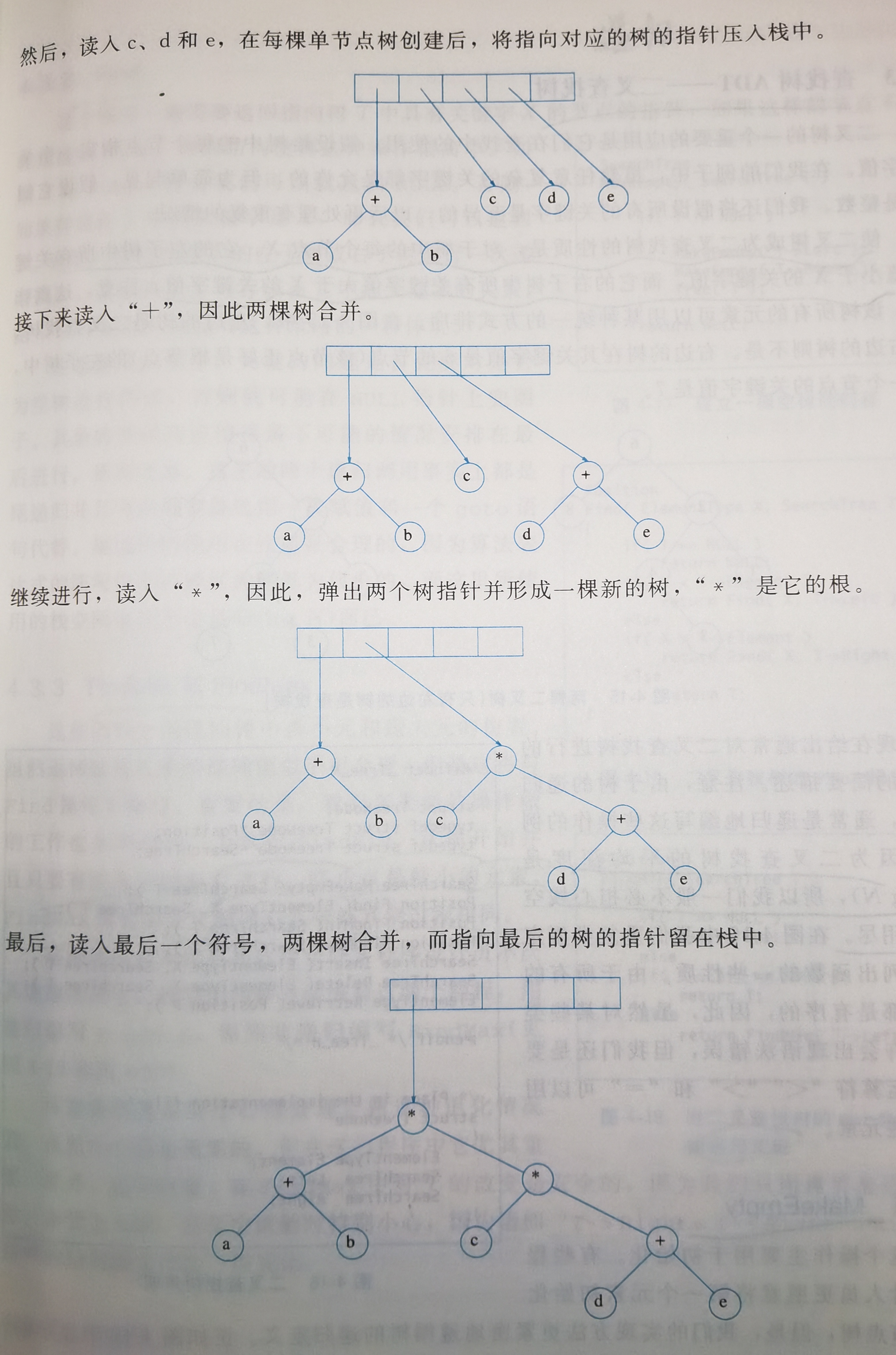
如果符号是操作符，从栈中弹出指向两棵树\(T_1\)和\(T_2\)的两个指针（\(T_1\)的先弹出）并形成一棵新的树，该树的根就是操作符，它的左、右儿子分别指向\(T_2\)和\(T_1\)。然后将指向这棵新树的指针压入栈中。

4.3 查找树ADT——二叉查找树

特征：对于树中的每个节点\(X\)，它的左子树中所有关键字值小于\(X\)的关键字值，而它的右子树中所有关键字值大于\(X\)的关键字值。
二叉查找树的类型声明：

#ifndef _Tree_H

struct TreeNode;
typedef struct TreeNode *Position;
typedef struct TreeNode *SearchTree;

SearchTree MakeEmpty( SearchTree T );
Position Find( ElementType X, SearchTree T );
Position FindMin( SearchTree T );
Position FindMax( SearchTree T );
SearchTree Insert( ElementType X, SearchTree T );
SearchTree Delete( ElementType X, SearchTree T );
ElementType Retrieve( Position P );

#endif /* _Tree_H */

/* Place in the implementation file */
struct TreeNode
{
 ElementType Element;
 SearchTree Left;
 SearchTree Right;
}

因为二叉查找树的平均深度为\(O(\log{N})\)，所以一般不必担心栈空间被用尽。

具体函数实现：

 /* Make T empty */
SearchTree
MakeEmpty( SearchTree T )
{
 if( T != NULL )
 {
  MakeEmpty( T->Left );
  MakeEmpty( T->Right );
  free( T );
 }
 return NULL;
}

/* Find X's position in T */
Position
Find( ElementType X, SearchTree T)
{
 if( T == NULL )
  return NULL;
 if( X < T->Element )
  return Find( X, T->Left );
 else
 if( X > T->Element )
  return Find( X, T->Right );
 else
  return T;
}

/* Find min's position in T(recursion)*/
Position
FindMin( SearchTree T )
{
 if( T == NULL )
  return NULL;
 else
 if( T->Left == NULL)
  return T;
 else
  return FindMin( T->Left );
}

/* Find max's position in T(not recursion)*/
Position
FindMax( SearchTree T )
{
 if( T != NULL )
  while( T->Right != NULL )
   T = T->Right;
 return T;
}

/* Insert X in T */
SearchTree
Insert( ElementType X, SearchTree T )
{
 if( T == NULL )
 {
  /* Create and return a one-node tree */
  T = malloc( sizeof( struct TreeNode ) );
  if( T == NULL)
   FatalError( "Out of space!!!" );
  else
  {
   T->Element = X;
   T->Left = T->Right = NULL;
  }
 }
 else
 if( X < T->Element )
  T->Left = Insert( X, T->Left );
 else
 if( X > T->Element )
  T->Right = Insert( X, T->Right );
 /* Else X is in the tree already; we'll do nothing*/
 return T;
}

/* Delete X in T*/
/*
If X is a leaf, delete X directly.
If X has one child, make X's father point to X's child.
If X has two children, find min in right subtree, use it to replace X, and delete the min element.
*/
SearchTree
Delete( ElementType X, SearchTree T )
{
 Positon TmpCell;
 if( T == NULL )
  Error( "Element not found" );
 else
 if( X < T->Element ) /* Go left */
  T->Left = Delete( X, T->Left );
 else
 if( X > T->Element ) /* Go right */
  T->Right = Delete( X, T->Right );
 else /* Found element to be deleted */
 if( T->Left && T->Right ) /* Two children */
 {
  /* Replace with smallest in right subtree */
  TmpCell = FindMin( T->Right );
  T->Element = TmpCell->Element;
  T->Right = Delete( T->Element, T->Right );
 }
 else /* One or zero children*/
 {
  TmpCell = T;
  if( T->Left == NULL) /* Also handles 0 children */
   T = T->Right;
  else if( T->Right == NULL )
   T = T->Left;
  free( TmpCell );
 }
 return T;
}

如果删除的次数不多，则通常使用的策略是懒惰删除(lazy deletion)：当一个元素要被删除时，它仍留在树中，只是做了个被删除的记号。

平均情形分析

除MakeEmpty外，所有的操作都是\(O(d)\)的，其中d是包含所访问的关键字的节点的深度。
一棵树的所有节点的深度的和称为内部路径长(internal path length)。
假设所有的树出现的机会均等，则树的所有节点的平均深度（平均内部路径长）为\(O(\log{N})\)。

4.4 AVL树

AVL(Adelson-Velskii 和 Landis)树是带有平衡条件的二叉查找树。
这个平衡条件必须要容易保持，而且必须保证树的深度是\(O(\log{N})\)。——要求左右子树具有相同的高度/要求每个节点都必须要有相同高度的左子树和右子树。
一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。（空树的高度定义为-1）
在AVL树中插入一个节点可能会破坏AVL树的特性，所以需要把性质恢复以后才认为这一步插入完成。——旋转(rotation)
出现不平衡的四种情况（将必须重新平衡的节点叫作\(α\)）：

对\(α\)的左儿子的左子树进行一次插入。
对\(α\)的左儿子的右子树进行一次插入。
对\(α\)的右儿子的左子树进行一次插入。
对\(α\)的右儿子的右子树进行一次插入。

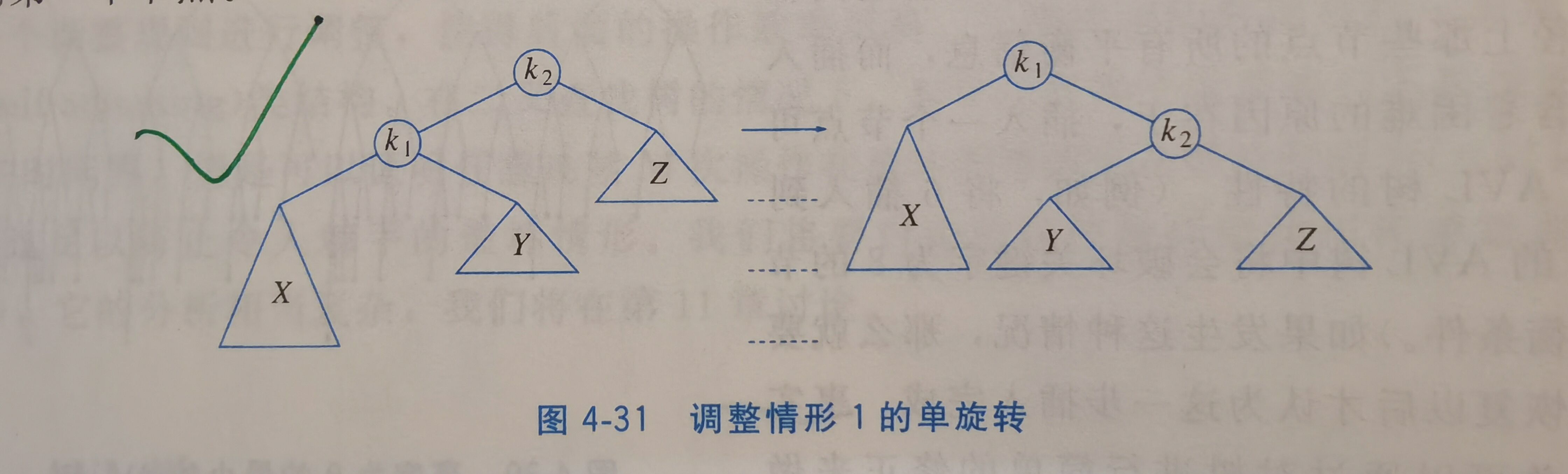
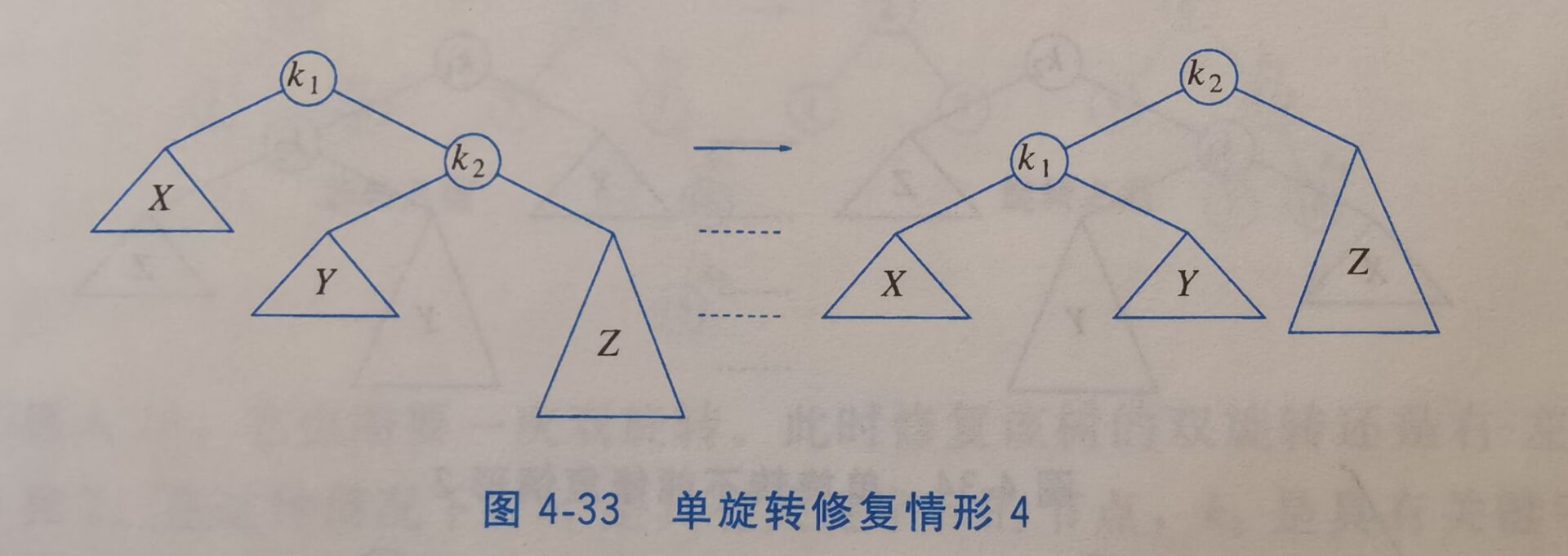
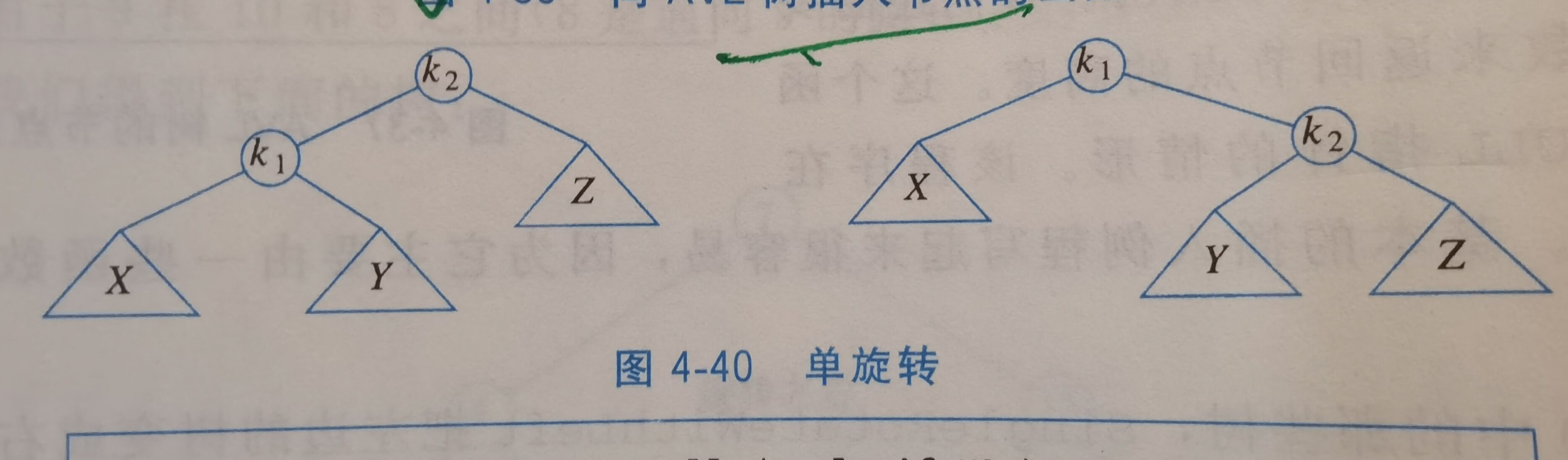
对于情形1和4，采用单旋转(single rotation)。
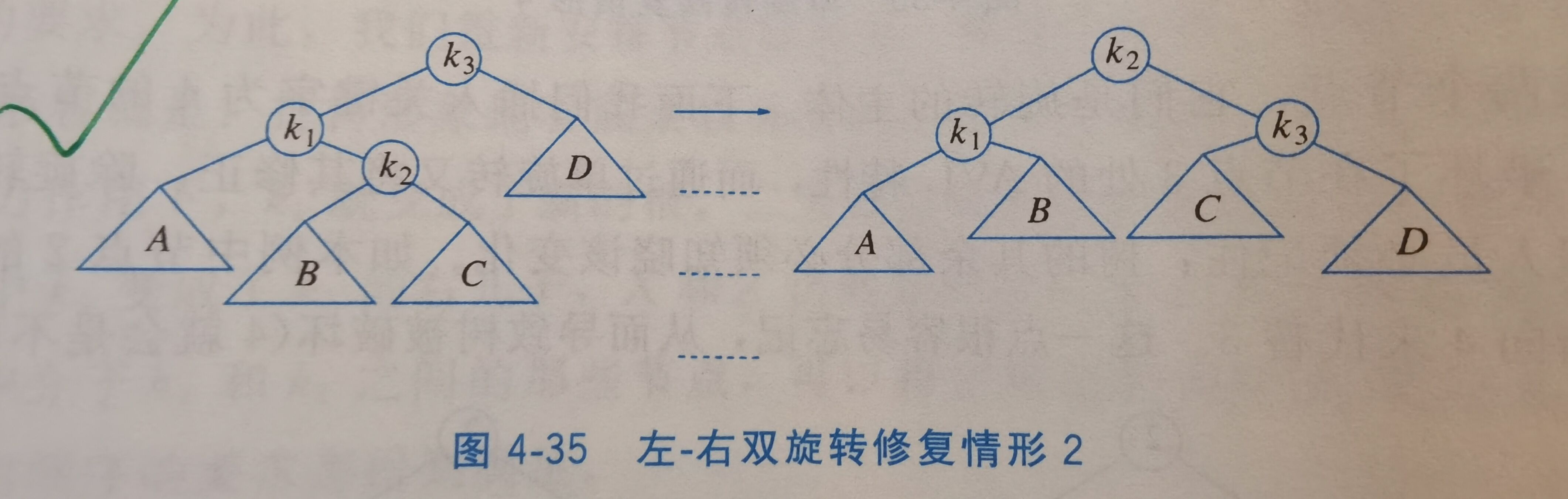
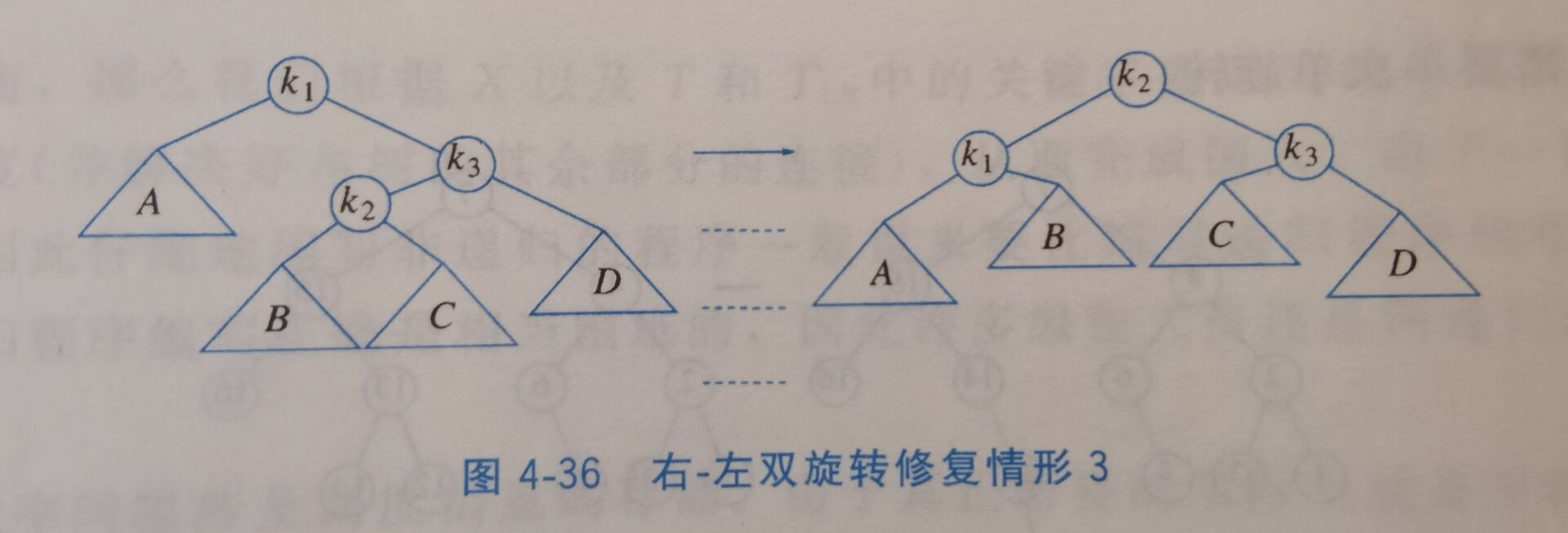
对于情形2和3，采用双旋转(double rotation)。

4.4.1 单旋转

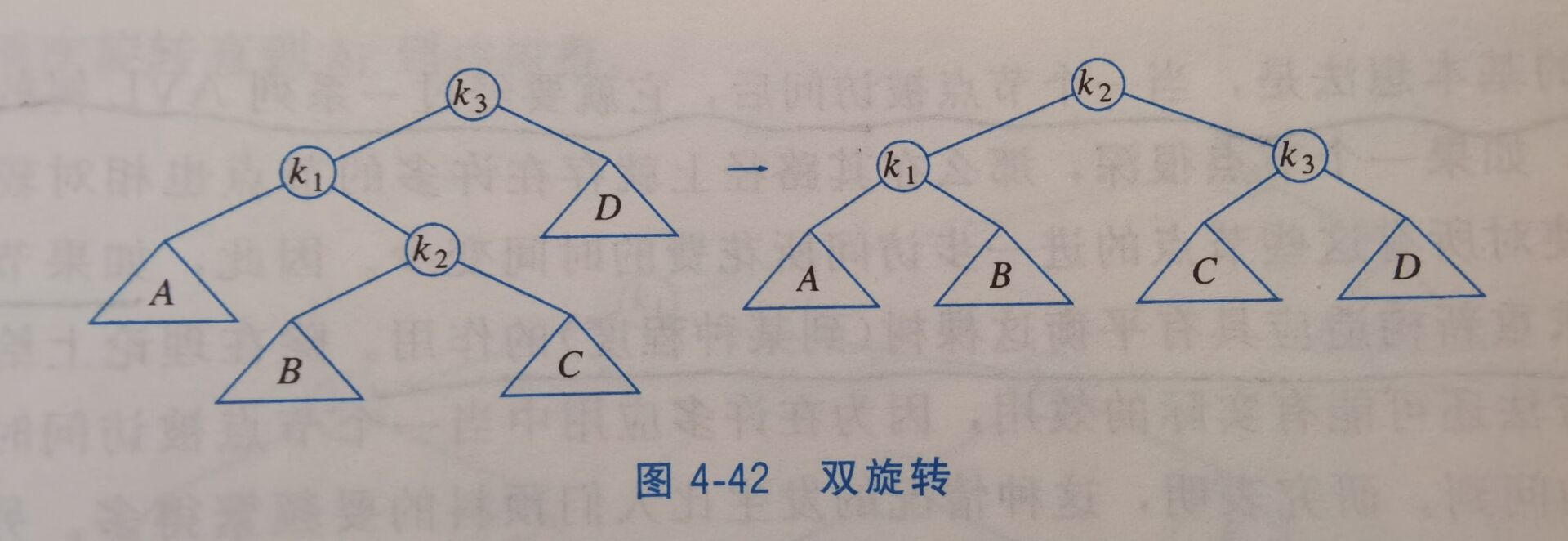
4.4.2 双旋转

4.4.3 函数实现

AVL树的节点声明：

#ifndef _AvlTree_H

struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;

AvlTree MakeEmpty( AvlTree T );
Position Find( ElementType X, AvlTree T );
Position FindMin( AvlTree T );
Position FindMax( AvlTree T );
AvlTree Insert( ElementType X, AvlTree T );
AvlTree Delete( ElementType X, AvlTree T );

#endif /* _AvlTree_H */

/* Place in the implementation file */
struct AvlNode
{
 ElementType Element;
 AvlTree Left;
 AvlTree Right;
 int Height;
}

AVL树本质上还是二叉查找树，具体函数实现其实大同小异。

具体函数实现：

/* Return one node's height */
static int
Height( Position P )
{
 if( P == NULL )
  return -1;
 else
  return P->Height;
}

/* Insert X in T */
AvlTree
Insert( ElementType X, AvlTree T )
{
 if( T == NULL )
 {
  /* Create and return a one-node tree */
  T = malloc( sizeof( struct AvlNode ) );
  if( T == NULL )
   FatalError( "Out of space!!!");
  else
  {
   T->Element = X; T->Height = 0;
   T->Left = T->Right = NULL;
  }
 }
 else
 if( X < T->Element )
 {
  T->Left = Insert( X, T->Left );
  if( Height( T->Left ) - Height( T->Right ) == 2 )
   if( X < T->Left->Element )
    T = SingleRotateWithLeft( T );
   else
    T = DoubleRotateWithLeft( T );
 }
 else
 if( X > T->Element )
 {
  T->Right = Insert( X, T->Right );
  if( Height( T->Right ) - Height( T->Left ) == 2 )
   if( X > T->Right->Element )
    T = SingleRotateWithRight( T );
   else
    T = DoubleRotateWithRight( T );
 }
 /* Else X is in the tree already; we'll do nothing */
 T->Height = Max( Height( T->Left ), Height( T->Right ) ) + 1;
 return T;
}

/* This function can be called only if K2 has a left child */
/* Perform a rotate between a node (K2) and its left child */
/* Update heights, then return new root */
static Position
SingleRotateWithLeft( Position K2 )
{
 Position K1;
 K1 = K2->Left;
 K2->Left = K1->Right;
 K1->Right = K2;
 K2->Height = Max( Height( K2->Left ), Height( K2->Right ) ) + 1;
 K1->Height = Max( Height( K1->Left ), K2->Right ) + 1;
 return K1; /* New root */
}

/* This function can be called only if K3 has a left child and K3's left child has a right child */
/* Do the left-right double rotation */
/* Update heights, then return new root */
static Position
DoubleRotationWithLeft( Position K3 )
{
 /* Rotate between K1 and K2 */
 K3->Left = SingleRotateWithRight( K3->Left );
 /* Rotate between K3 and K2 */
 return SingleRotateWithLeft( K3 );
}

这里的双旋转是利用两次单旋转来实现的。

4.5 伸展树(splay tree)

伸展树保证从空树开始任意连续M次对树的操作最多花费\(O(M\log{N})\)时间。
一般说来，当M次操作的序列总的最坏情形运行时间为\(O(MF(N))\)时，我们就说它的摊还(amortized)运行时间为\(O(F(N))\)。
因此，一棵伸展树每次操作的摊还代价是\(O(\log{N})\)。

如果任意特定操作可以有最坏时间界\(O(N)\)，而我们仍然要求一个\(O(\log{N})\)的摊还时间界，那么很清楚，只要一个节点被访问，它就必须被移动，否则，一旦我们发现一个深层的节点，我们家有可能不断对它进行Find操作。如果这个节点不改变位而每次访问又花费\(O(N)\)，那么M次访问将花费\(O(M·N)\)的时间。

伸展树的基本想法是，当一个节点被访问后，它就要经过一系列AVL树的旋转后放到根上。如果节点过深，那么我们还要求重新构造应具有平衡这棵树（到某种程度）的作用。

4.5.1 一个简单的想法

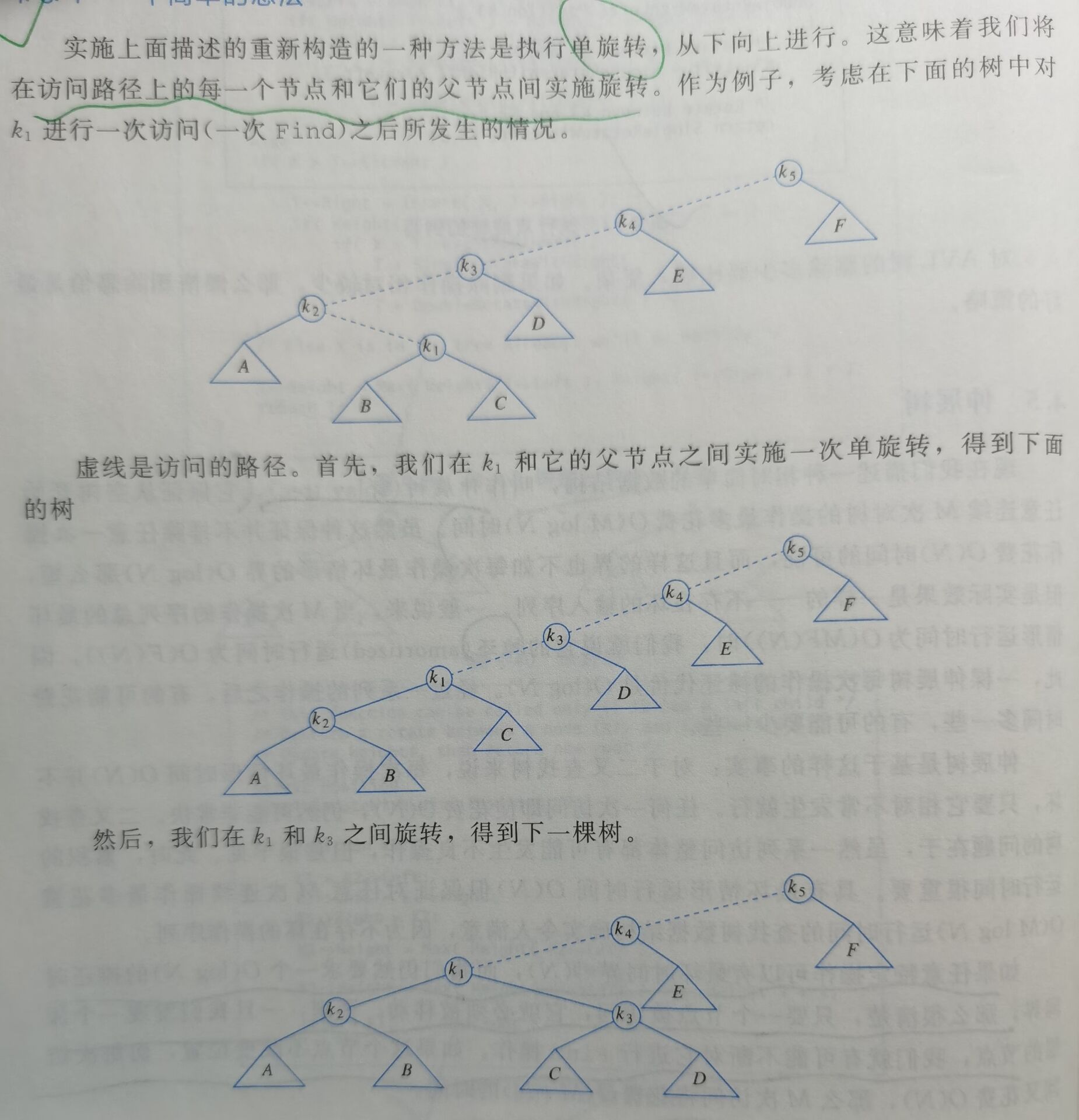
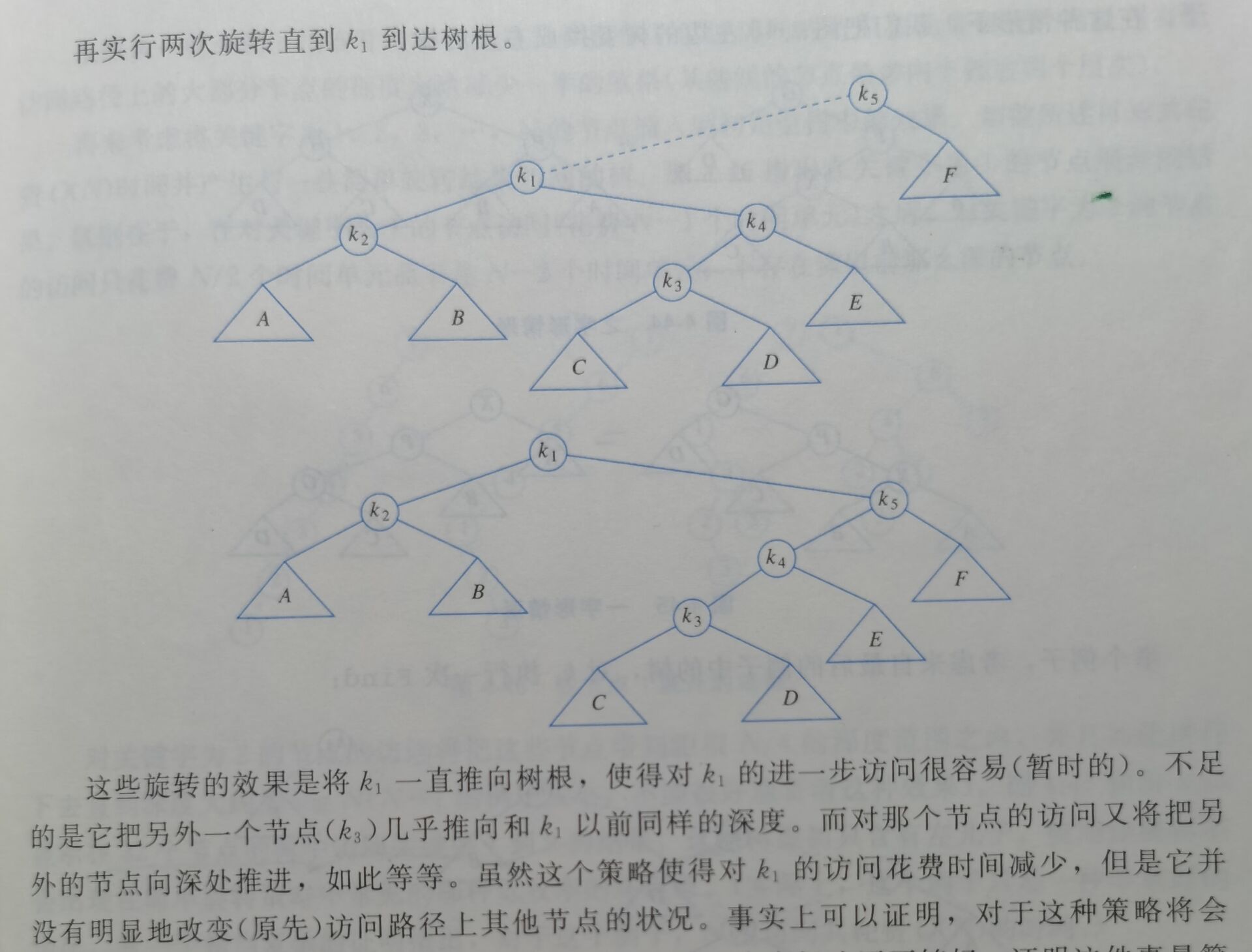
无论如何，缺陷很大。

4.5.2 展开(splaying)

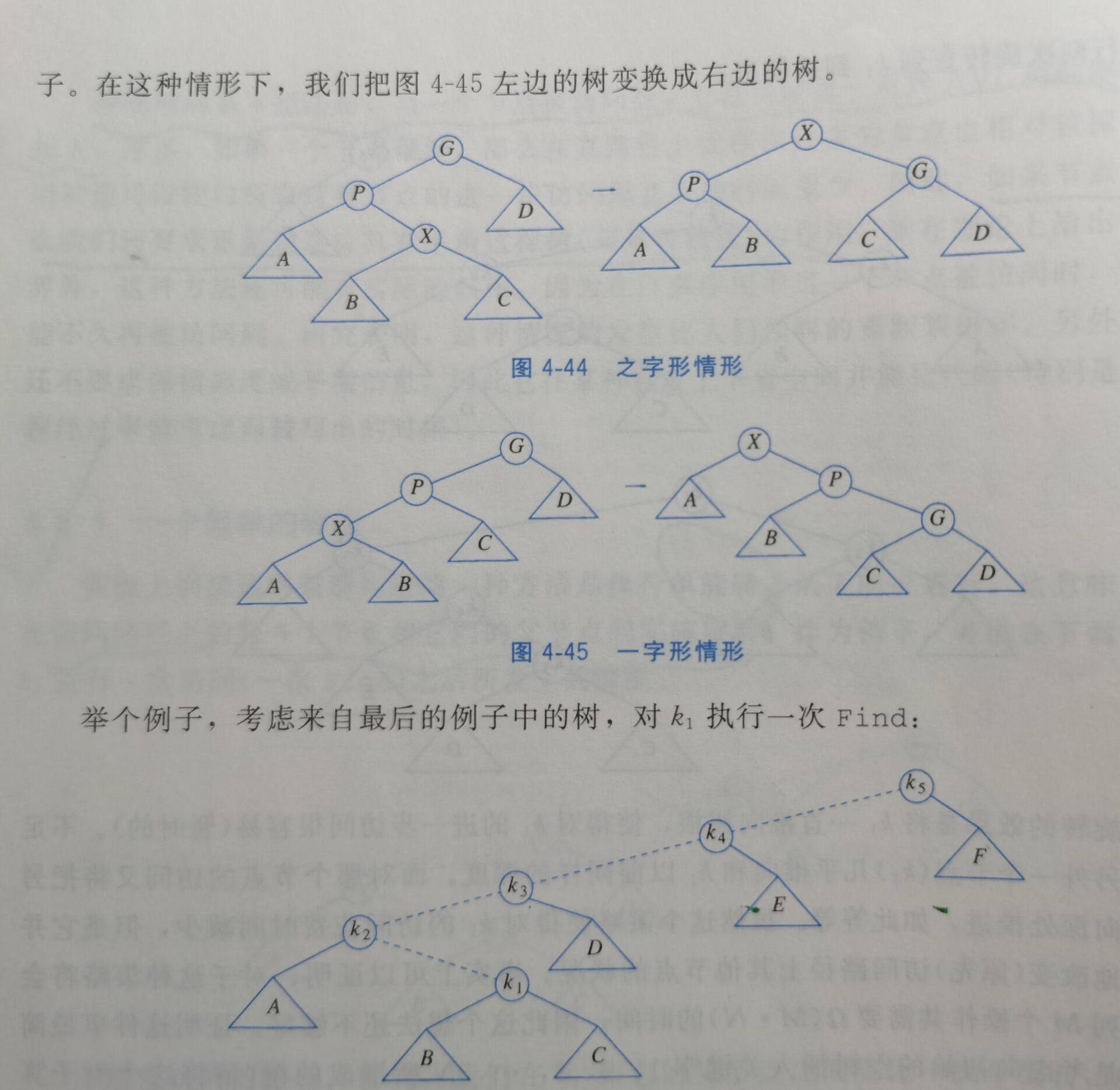
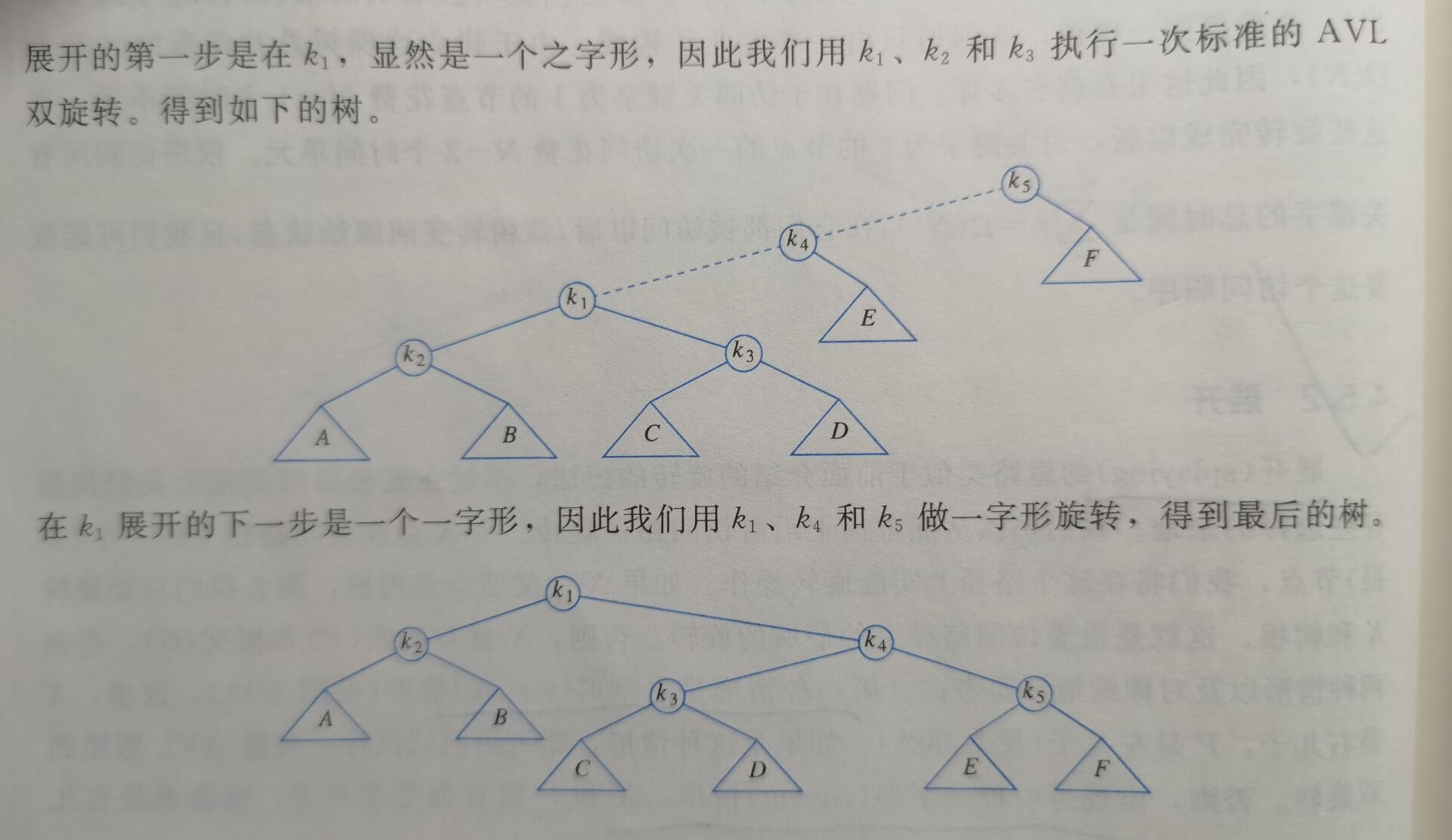
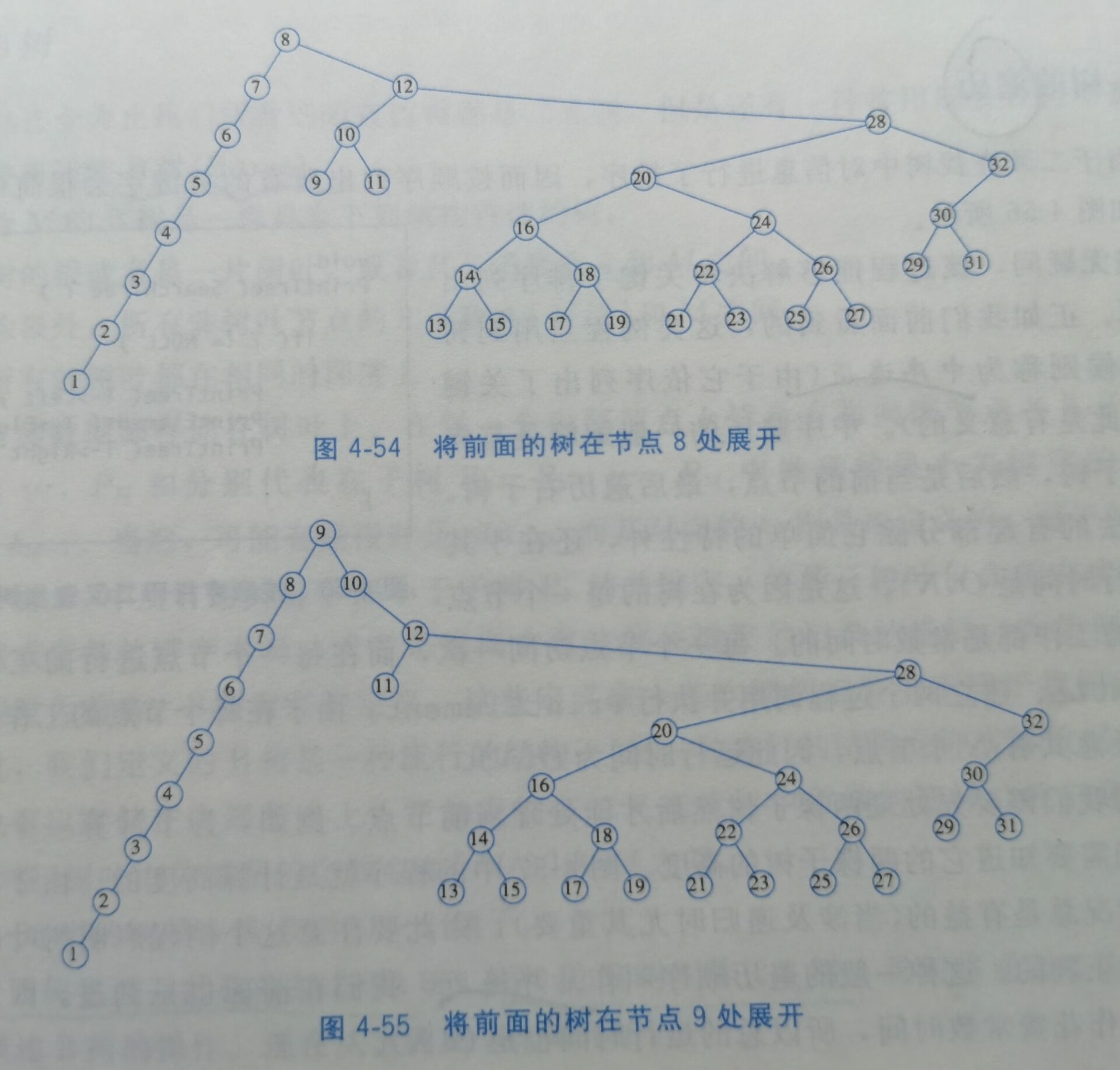
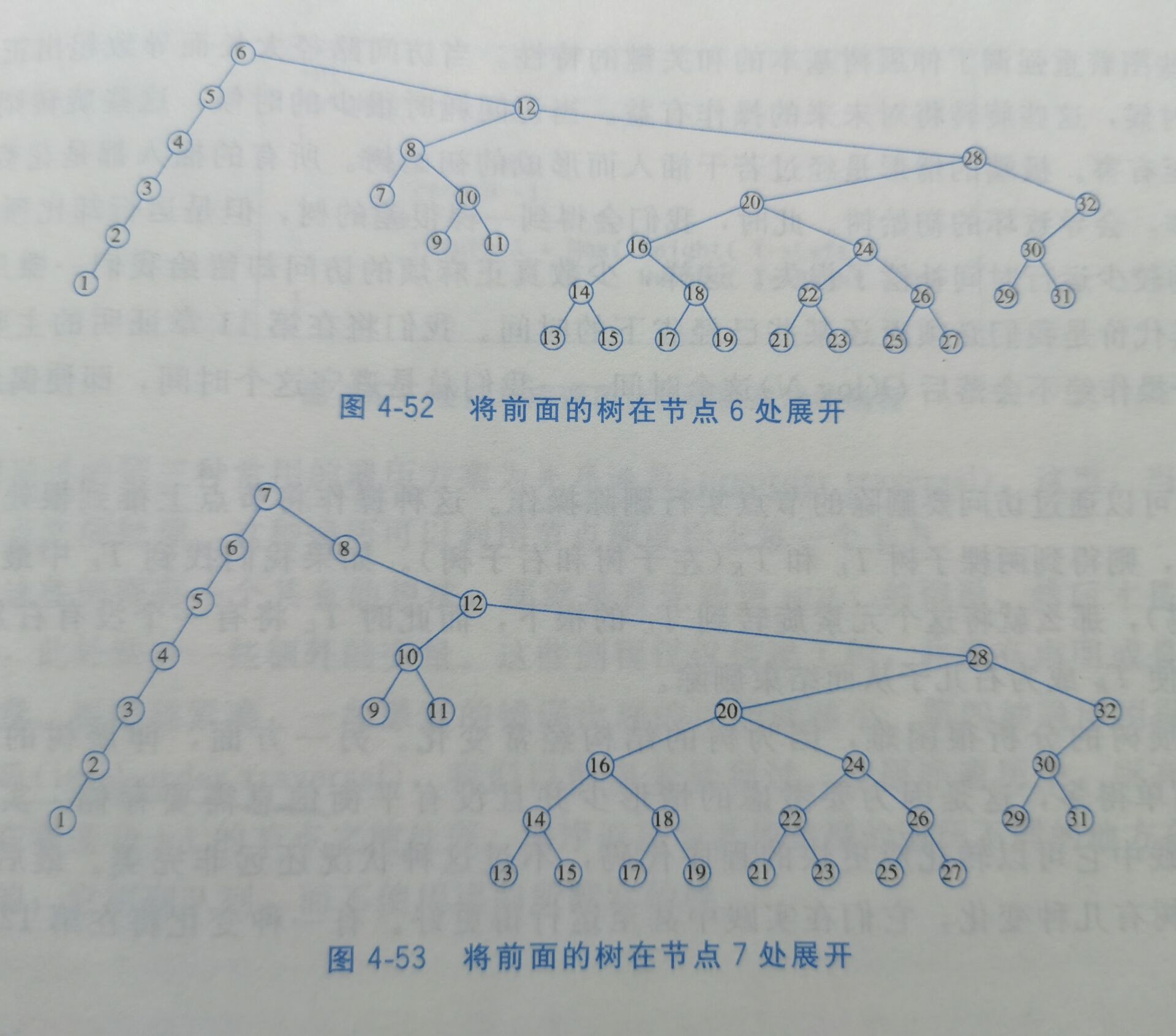
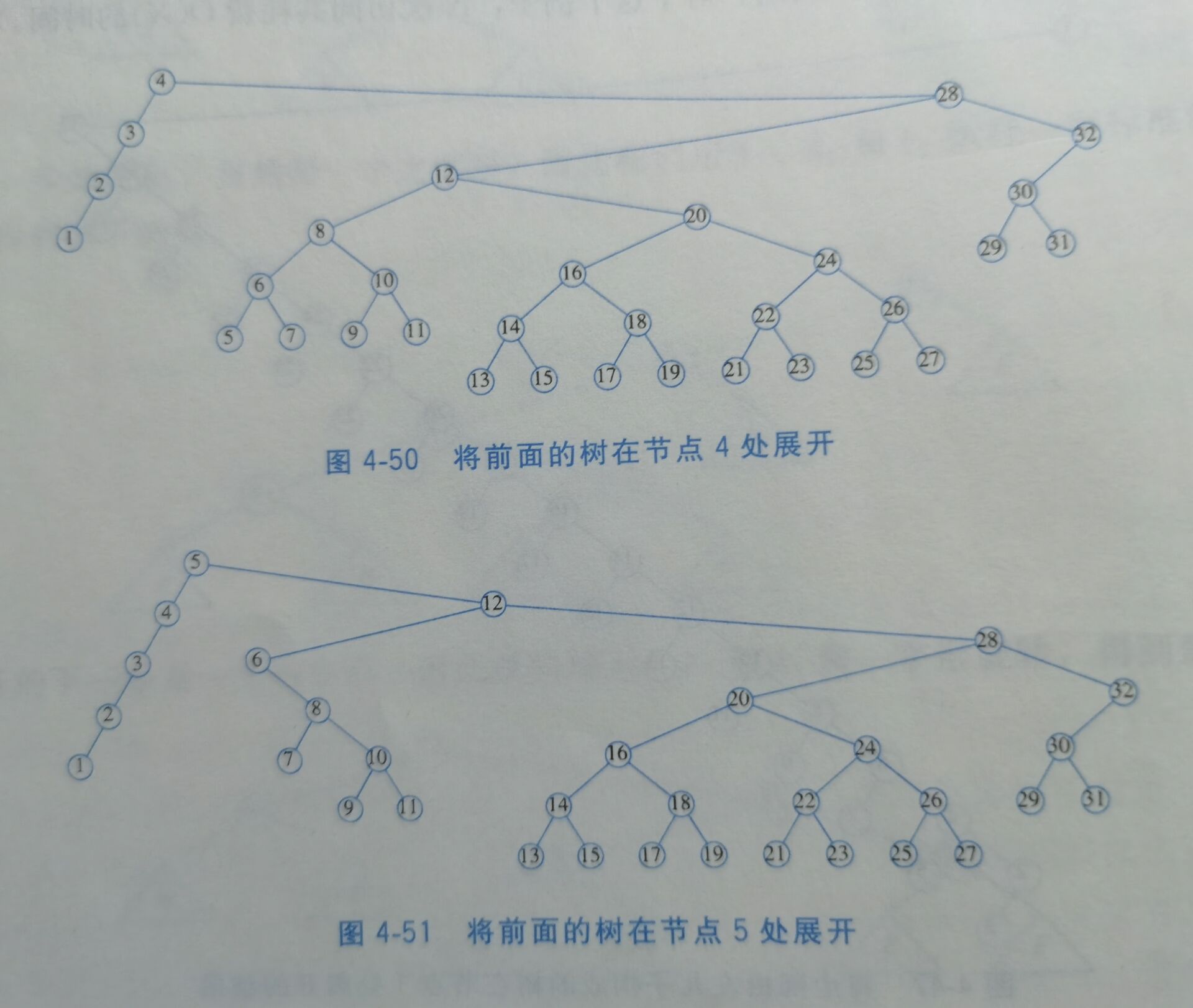
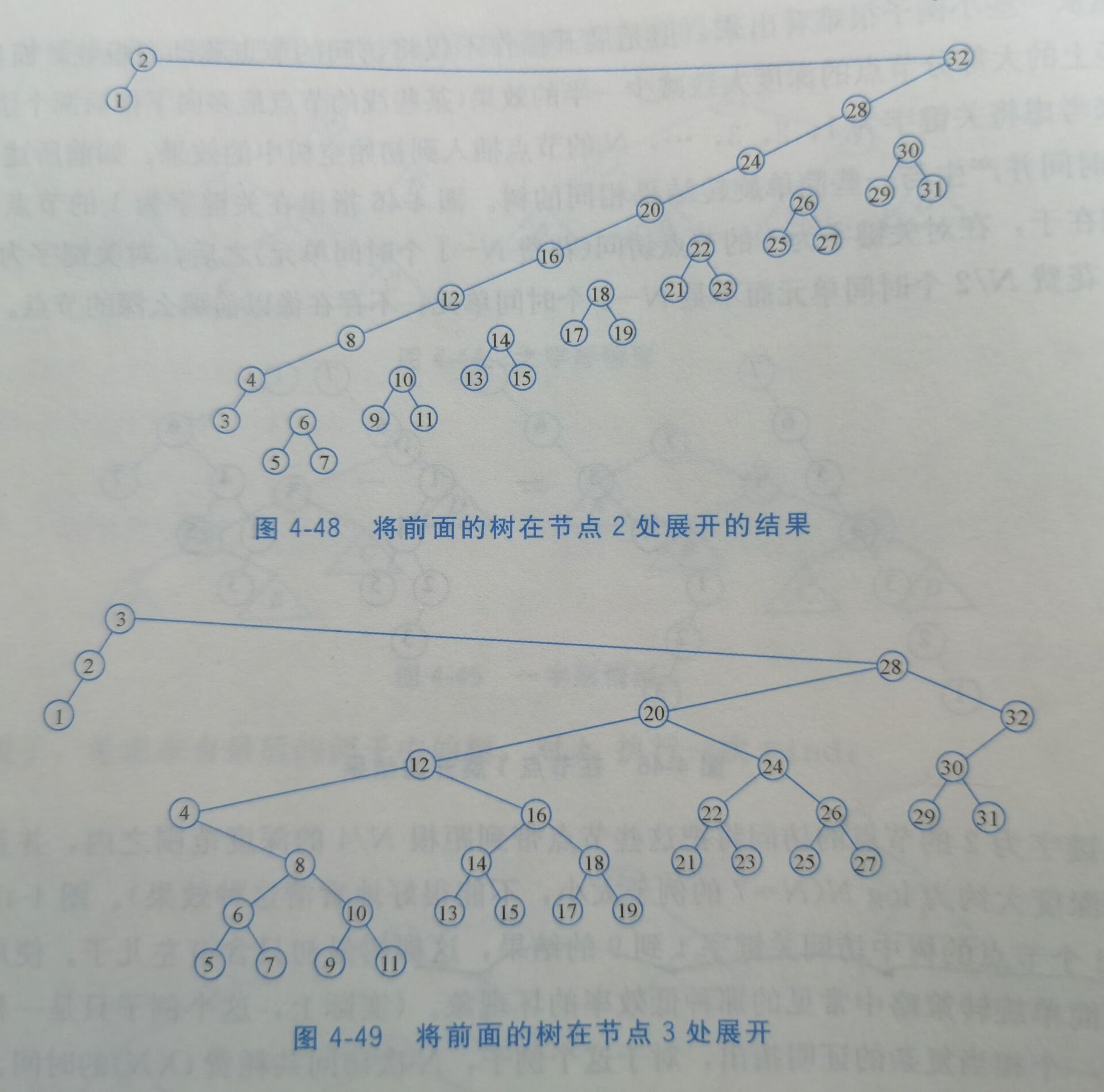
4.6 树的遍历

中序遍历(inorder traversal)
后序遍历(postorder traversal)
先序遍历(preorder traversal)
层序遍历(level-order traversal)——在层序遍历中，所有深度为\(D\)的节点要在深度\(D+1\)的节点之前处理。层序遍历与其他类型的遍历不同的地方在于它不是递归实施的；它用到队列，而不使用递归所默示的栈。

4.7 B树(B-tree)

阶为\(M\)的B树是一棵具有下列结构特性的树：

树的根或者是一片树叶，或者其儿子数在\(2\)和\(M\)之间。
除根外，所有非树叶节点的儿子数在\(⌈M/2⌉\)和\(M\)之间。
所有的树叶都在相同的深度上。

4阶B树常被称作2-3-4树，3阶B树常被称作2-3树。
下面举一棵2-3树的例子：

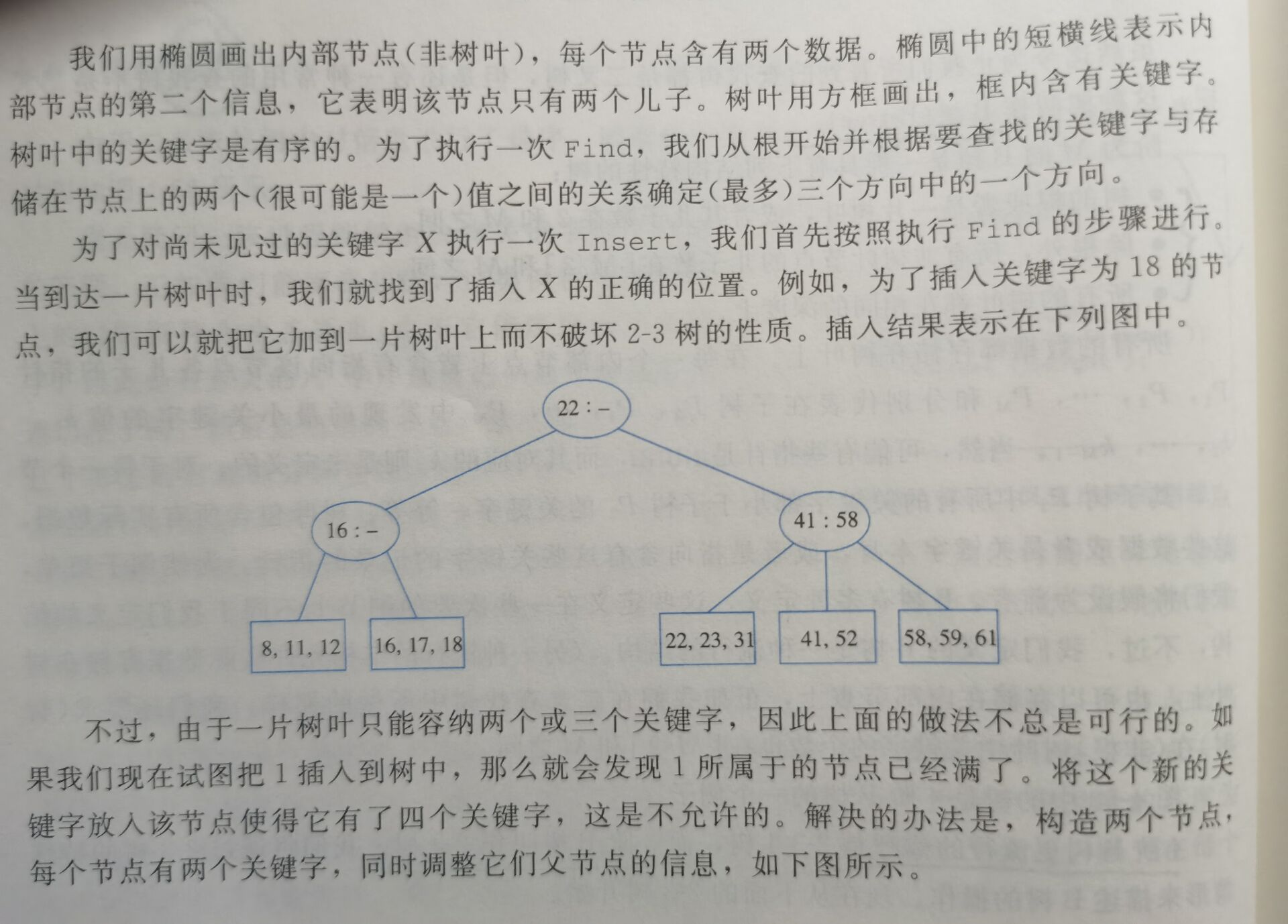
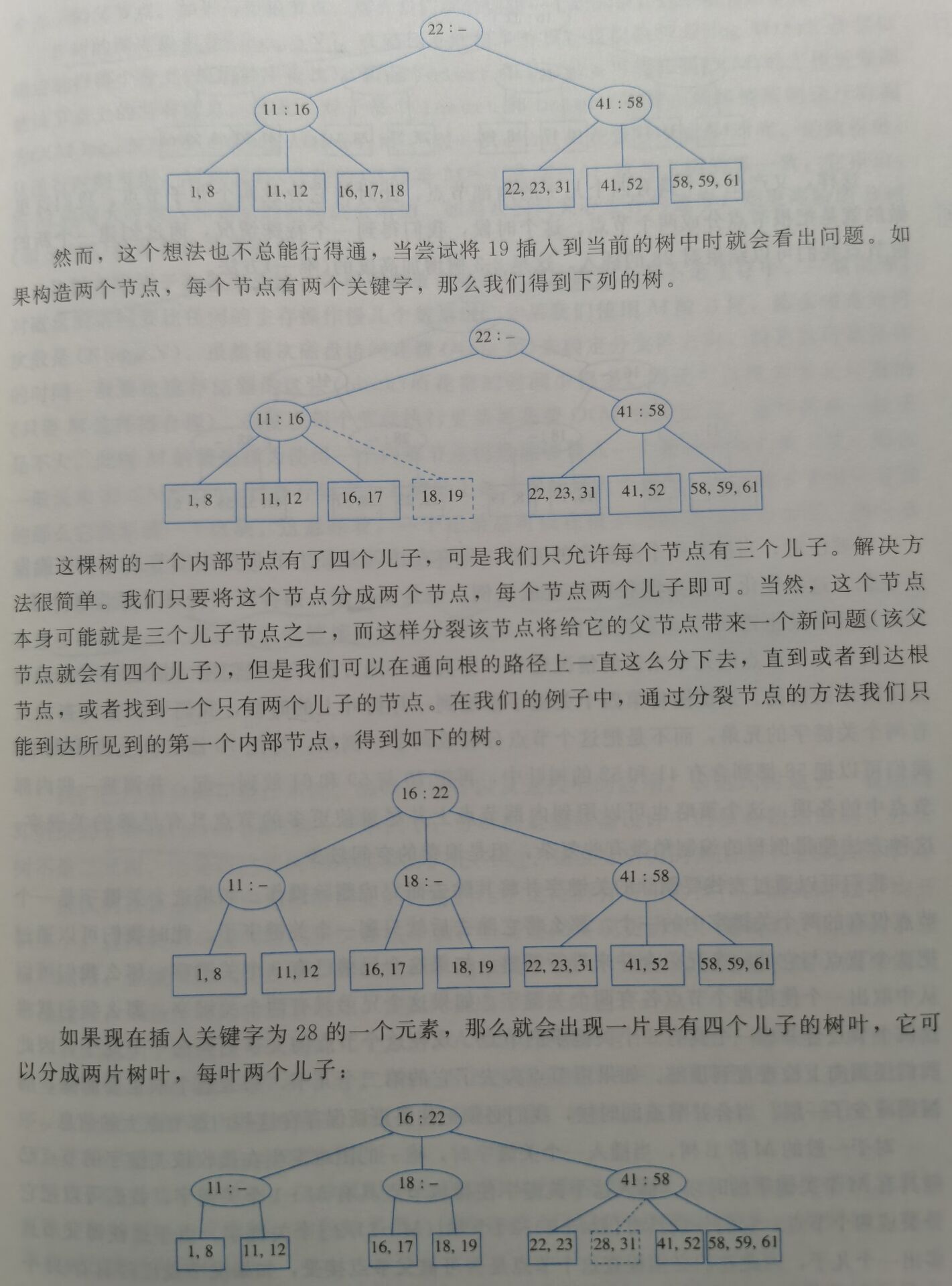
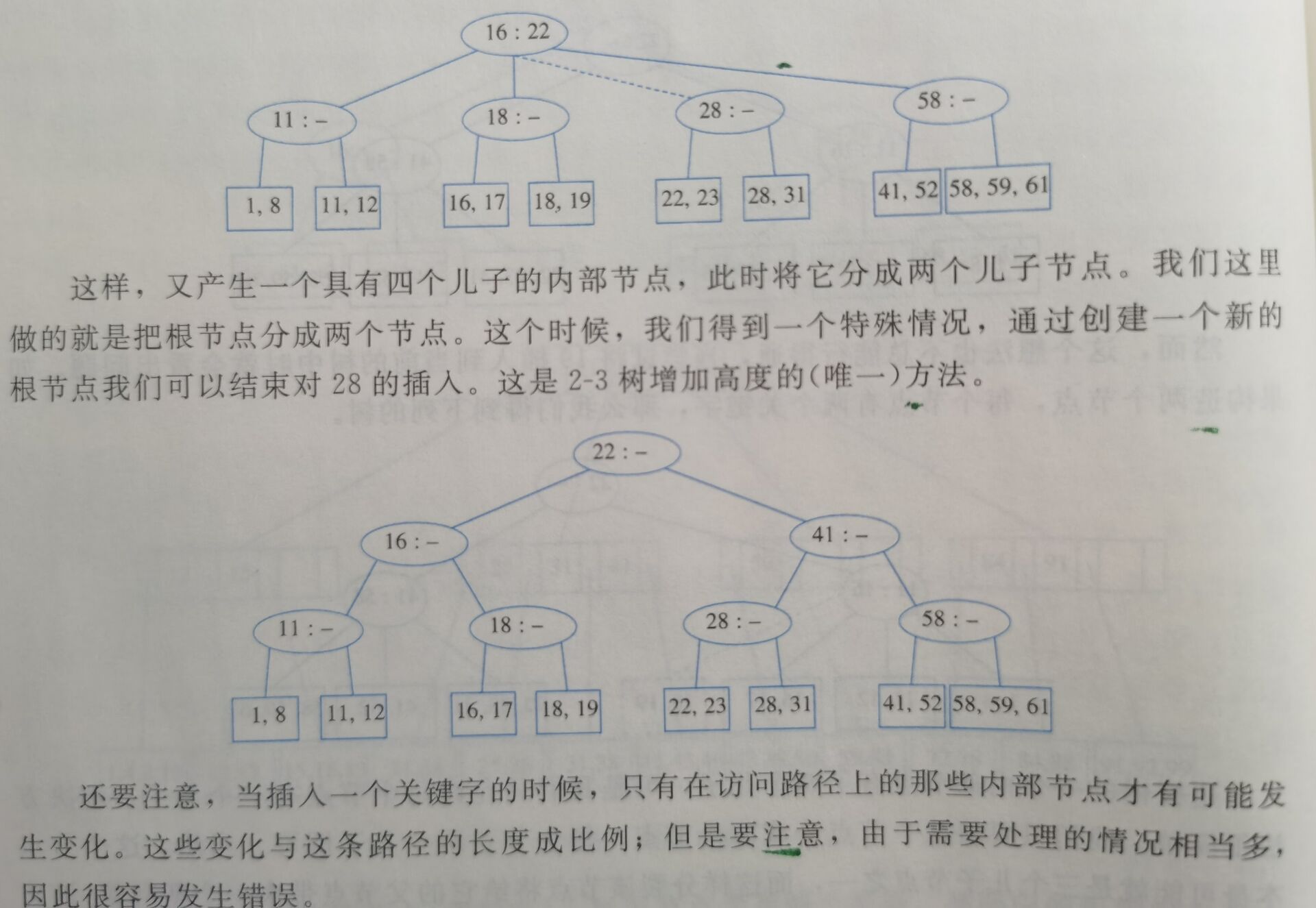
B树的深度最多是\(⌈\log_{⌈M/2⌉}{N}⌉\)。
B树实际用于数据库系统，在那里树被存储在物理的磁盘上而不是主存中。
分析指出，一棵B树将被占满\(\ln{2}\) = \(69\)%。当一棵树得到它的第\((M + 1)\)项时，例程不是总去分裂节点，而是搜索能够接纳新儿子的兄弟，此时我们能够更好地利用空间。

posted @ 2022-09-19 22:10 kirin-dev 阅读(139) 评论(0) 收藏举报

刷新页面返回顶部

kirin-dev

数据结构与算法分析——C语言描述（第4章 树）