正整数n的不同分解式个数

正整数n的不同分解式个数

如题：

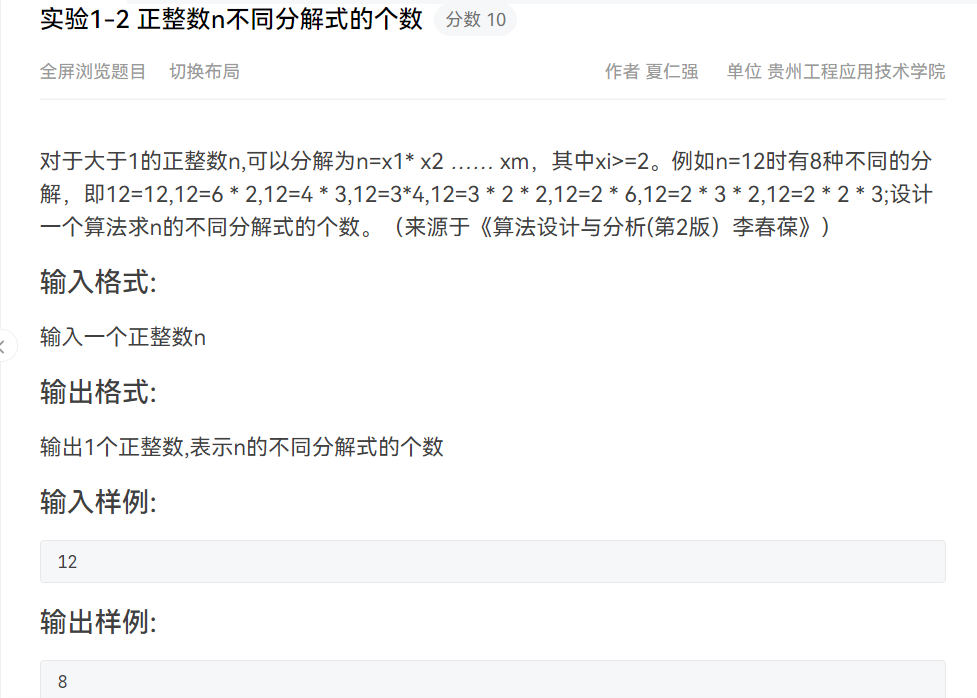
思路：

使用动态规划的思想（DP思路，即一个大一点规模的问题可以被拆解为更小的，更容易解决的问题）

首先，定义一个数组 dp，用来存储每个数的分解式个数。 dp[i] 表示当前数 i 的不同分解式的个数。

接下来，从数 2 开始循环，逐个计算每个数的分解式个数。dp[i] = 0，防止数组越界。

然后，通过枚举当前数的所有因子来计算分解式个数。使用一个内部循环，从因子

j = 1 开始，一直到 i/2（因为因子的最大可能值是 i/2）。对于每个因子 j，计算

i % j == 0。如果是整除关系，说明 j 是 i 的一个因子。

在这种情况下，我们根据递推公式 dp[i] += dp[j] 来计算当前数的分解式个数。dp[j] 表示之前计算的拥有因子 j 的数的分解式个数。

根据递推公式，我们将之前计算的结果 dp[j] 累加到 dp[i] 上。这样就实现了动态规划的思想，利用已知的结果计算新的结果。

最后，循环结束后，返回数组 dp[n] 的值，即正整数 n 的不同分解式的个数。

代码：

以n=12，

第十一次循环（i = 12）：

• dp[12] = 0
• 内层循环（j = 1）：12 % 1 == 0，所以 dp[12] += dp[1] = 0 + 1 = 1
• 内层循环（j = 2）：12 % 2 == 0，所以 dp[12] += dp[2] = 1 + 1 = 2
• 内层循环（j = 3）：12 % 3 == 0，所以 dp[12] += dp[3] = 2 + 1 = 3
• 内层循环（j = 4）：12 % 4 == 0，所以 dp[12] += dp[4] = 3 + 2 = 5
• 内层循环（j = 5）：12 % 5 != 0，跳过
• 内层循环（j = 6）：12 % 6 == 0，所以 dp[12] += dp[6] = 5 + 3 = 8
• 内层循环完毕
• dp[12] = 8

#include<stdio.h>

int countSum(int n){

    int dp[n+1]; //存储每个数的分解式个数
    dp[1] = 1;  // 输入 1 的时候为 1

    for(int i = 2; i <= n; i++){
        dp[i] = 0;  //用 dp[j] 计算 dp[i]
        
        for(int j = 1; j <= i/2; j++){ //因子的最大可能值是 i/2, 题目意思防止 1*12，,12*1
            if(i % j == 0){           //整除关系，说明 j 是 i 的一个因子
                                      //dp[i] 则是待计算的当前数 i 的分解式个数, dp[j] 表示之前计算的拥有因子 j 的数的分解式个数
                dp[i] += dp[j];      //一个数的分解式个数等于因子的分解式个数之和
            }
        }
    }
    
    return dp[n];
}

int main(){

    int n;
    scanf("%d", &n);

    int count = countSum(n);
    printf("%d", count);

    return 0;

}

很好，随机测试几个数，没啥问题，复制粘贴

好好好

最后一个测试点超时

做出一些修改

j 因子的范围从1到 i/2 改为2到 根号i

j 因子，对应的因子 i/j（ !=j ），并将两个因子的分解式个数都累加到dp[i]中

    for(int i = 2; i <= n; i++){
        dp[i] = 1;  //用 dp[j] 计算 dp[i]
        int limit = sqrt(i);

        for(int j = 2; j <= limit; j++){ //因子的最大可能值是根号 i
            if(i % j == 0){           //整除关系，说明 j 是 i 的一个因子
                                      //dp[i] 则是待计算的当前数 i 的分解式个数, dp[j] 表示之前计算的拥有因子 j 的数的分解式个数
                int other_factor = i / j;
                dp[i] += dp[j];
                if(other_factor != j){    //因子 i/j（!=j），将两个因子的分解式个数都累加到dp[i]中
                    dp[i] += dp[other_factor];
                }
            }
        }
    }

n的取值过大的时候，耗时还是小高，但是过了所有测试点

---

使用递归

#include <stdio.h>

int total = 0;

void solve(int n) {
    if (n == 1)
        total++;
    else {
        for (int i = 2; i <= n; i++)
            if (n % i == 0)
                solve(n / i);
    }
}

int main() {
    int n;
    scanf("%d", &n);

    solve(n);

    printf("%d", total);

    return 0;
}