分解质因数

分解质因数

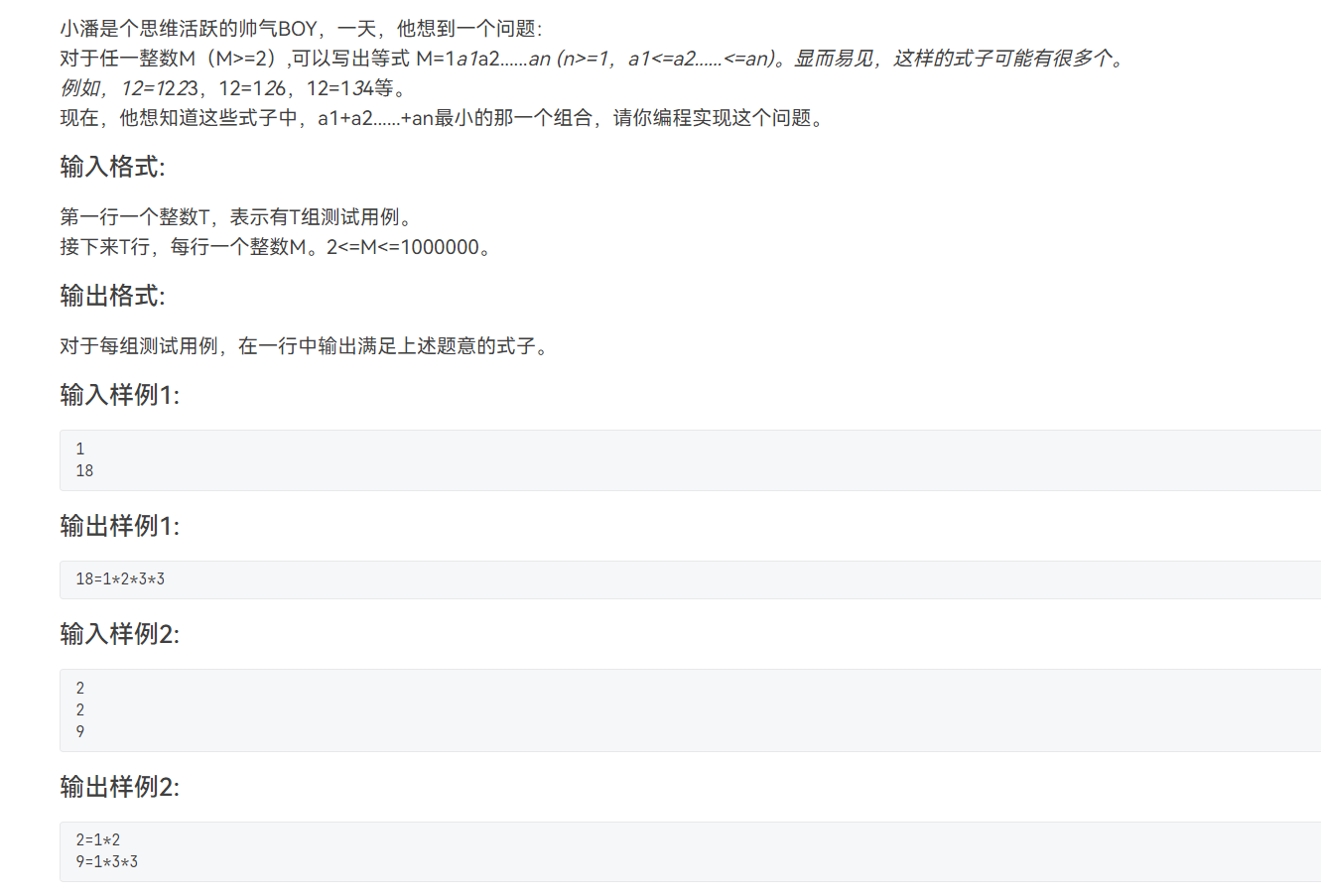
如题：

思路：

短除法

代码：

#include <stdio.h>
#include <math.h>

// 用函数。保持主函数的可读性吧
void decomposeMinSum(int M) {
    printf("%d=", M);

    //所有整数的最小正因数1
    if (M != 1) {
        printf("1*");
    }

    int factor = 2; // 起始质因数为 2
    int limit = sqrt(M); // 上限为 M 的平方根, 大数字可以循环少
    
    // 循环查找质因数
    while (M > 1 && factor <= limit) {
        // 如果 M 可以被 factor 整除，则输出 factor
        if (M % factor == 0) {
            printf("%d", factor);
            M /= factor;
            
            // 如果 M 不等于 1，则输出乘号， 说明还有质因数
            if (M != 1) {
                printf("*");
            }
        } 
        else {
            factor++;
        }
    }

    // 如果 M 不等于 1，则输出剩余的 M
    if (M != 1) {
        printf("%d", M);
    }
    
    printf("\n");
}

int main() {
    int T;
    scanf("%d", &T);
    
    for (int i = 0; i < T; i++) {
        int M;
        scanf("%d", &M);
        
        // 调用分解质因数函数
        decomposeMinSum(M);
    }
    
    return 0;
}

举例说明：

以数字 18 为例：

1. 首先，在 main() 函数中读取测试用例的数量 T，将其设置为 1。然后循环读取一个测试用例，即将数字 18 存入变量 M 中。
2. 调用 decomposeMinSum(18) 函数，打印出 18=1*。
3. 循环开始，factor 的初始值为 2，而 limit 的值计算为sqrt(18) ，即 4。由于 M 可以被 2 整除，因此打印出 2，并将 M 的值更新为 M /= factor = 9。
4. M 现在等于 9，factor 等于 2，因为 9 不能被 2 整除，所以将 factor 加 1 更新为 3。
5. 现在 factor 等于 3，3 能够整除 9，所以打印出 3，并将 M 更新为 M /= factor，即 M = 3。
6. 因为此时 M 等于 3，而 3 是质数，所以不再进行循环，直接打印出 3。
7. 程序结束，输出的结果为 18=1*2*3*3。