【高中】概率统计笔记

更新于：2020年4月13日.

更新于：2020年10月13日.

近期的笔记整理。
将会不定期更新，若有版权问题请联系作者，将会立刻删除相关内容。

由于是一个人写的，暂时没有校对。整体上是正确的，可能会有小瑕疵。发现请及时联系作者。

引入

---

e.g.1

甲乙丙丁四个人做传球练习，球首先由甲传出，每个人得到球后都等概率地传给其余三个人之一，设\(P_n\)表示经过\(n\)次传递后球回到甲手中的概率，求\(P_n\)(以\(n\)表示过\(n\)次传递后球落在甲的手中）.

解答：
在一次传球中，球可以从【不是甲】传球给【甲】，此时

【当前甲的概率】=【上次球在乙手里并且往甲传的概率】+【上次球在丙手里并且往甲传的概率】+【上次球在丁手里并且往甲传的概率】：

\[P_n=(\frac{1-P_{n-1}}{3})\cdot \frac{1}{3}+(\frac{1-P_{n-1}}{3})\cdot \frac{1}{3}+(\frac{1-P_{n-1}}{3})\cdot \frac{1}{3} \]

所以

\[P_n=\frac{1-P_{n-1}}{3} \]

接下来凑系数：

\[P_n-\frac{1}{4}=-\frac{1}{3}\cdot (P_{n-1} - \frac{1}{4}) \]

第一次传球肯定甲手里莫得球，所以\(P_1=0\)
所以

\[P_n=\frac{1}{4}-\frac{1}{4}(-\frac{1}{3})^{n-1} \]

---

e.g.2

甲、乙、丙三人轮流投掷一枚质地均匀的正方体骰子，规则如下：如果某人某一次掷出\(1\)点，则下一次继续由此人掷，如果掷出其他点数，则另外两个人抓阎决定由谁来投掷，且第一次由甲投掷.设第\(n\)次由甲投掷的概率是\(p_n\)，由乙或丙投掷的概率均为\(q_n\).求数列的通项公式${ p_n } $.

解答：
考虑：【这一次是甲的概率】=【上一次甲是1点】+【上一次是乙不中1点，抓阄甲中了】+【上一次是后不中1点，抓阄甲中了】

\[p_n=\frac{1}{6} p_{n-1} + q_{n-1}\cdot \frac{5}{6} \cdot \frac{1}{2}+q_{n-1} \cdot \frac{5}{6}\cdot \frac{1}{2} \]

化简得：

\[p_n=\frac{1}{6} p_{n-1}+\frac{5}{6} q_{n-1} \]

我们知道，在第\(n-1\)次游戏的时候，甲乙丙三人投掷骰子的概率和是\(1\)，所以：

\[p_{n-1}+2q_{n-1}=1 \]

所以只要联立上式就可以得到

\[17p_n=p_{n-1}+5 \]

解得

\[p_n=\frac{2}{3}(-\frac{1}{4})^{n-1}+\frac{1}{3} \]

进阶（然而还是很简单）

---

e.g.3

有人玩掷正四面体骰子走跳棋的游戏，已知正四面体骰子四个面上分别印有\(A，B，C，D\)棋盘上标有第\(0\)站、第\(1\)站、第\(2\)站、.…、第\(100\)站.一枚棋子开始在第\(0\)站，棋手每掷一次骰子，若掷出后骰子为\(A\)面，棋子向前跳\(2\)站，若掷出后骰子为\(B，C，D\)中的一面，则棋子向前跳\(1\)站，直到棋子跳到第\(99\)站（胜利大本营）或第\(100\)站（失败大本营)时，该游戏结束.设棋子跳到第\(n\)站的概率为\(P_n\)\((n \in \mathbb{N})\).
(1)求\(n\)与\(P_n\)的关系.
(2)求玩该游戏获胜和失败的概率.

解答:
当前位置\(n\)可以从\(n-1\)或者\(n-2\)到达，所以

\[P_n=\frac{3}{4}P_{n-1}+ \frac{1}{4}P_{n-2} \]

特征方程为：

\[x^2-\frac{3}{4}x- \frac{1}{4}=0 \]

解得\(x_1=1,x_2= - \frac{1}{4}\)
待定系数：

\[设P_n=Ax_1^{n-1}+Bx_2^{n-1} \]

带入\(0\)和\(1\)两个特殊值进去解\(A,B\)

\[P_0=1=A+B \\ P_1=\frac{1}{4}=Ax_1+B \]

解得\(A=\frac{4}{5},B=\frac{1}{5}\)
所以

\[P_n=\frac{4}{5}+\frac{1}{5}\cdot (- \frac{1}{4})^n,n \leq 99 \]

那么获胜的概率就是：

\[P_{win}=P_{99}=\frac{4}{5}+\frac{1}{5}\cdot (- \frac{1}{4})^{99} \]

失败的概率就是：

\[P_{lost}=1-P_{win}=... \]

总之算失败的时候千万不要带回\(P_n\)的通项公式去算，因为你在\(99\)格子的时候已经赢了，不会继续往后面走，不符合\(P_n\)通项建立的前提条件\(n \leq 99\)，要是他直接问你失败的概率然后你没注意到你就裂开来

---

e.g.4

现对一群牛是否认为自己帅进行随机问卷调查.若不认为自己不帅记\(1\)分，若继认为自己帅记\(2\)分.每头牛认为自己帅概率均为\(\frac{2}{3}\),且每头牛认为自己是否帅的事件相互独立.在对所有牛进行随机问卷调查的过程中，记已调查过的累计得分恰为\(n\)分的概率为\(P_n\)，求数列${ P_n } $的通项公式.

解答：

Method 1:

【得到当前分的概率】= 【得到\(n-1\)分时再得\(1\)分的概率】+【得到\(n-2\)分时再得\(2\)分的概率】

\[P_n=\frac{1}{3}P_{n-1}+\frac{2}{3}P_{n-2} \]

或者我们换个方向思考；

Method 2:

因为得不到\(n\)分的时候只有一种情况，那就是你采访到n-1分的时候下一个遇到的牛认为自己帅，就把\(n\)分这个阶段跳过了。也就是：

1-【得到当前分的概率】= 【得到n-2分时再得2分的概率】

即：

\[1-P_n=\frac{2}{3} P_{n-1} \]

两种递推式殊途同归，解得：

\[P_n=\frac{3}{5}+\frac{2}{5}\cdot(-\frac{2}{3})^n \]

---

e.g.5​

袋中共有\(8\)个球，其中有\(5\)个白球，\(3\)个红球，这些球除颜色外完全相同，从袋中随机取出一球，如果取出红球，则把它放回袋中；如果取出白球，则该白球不再放回，并且另补一个红球放入袋中，重复上述过程\(n\)次后，袋中红球的个数记为\(X_n\).求随机变量\(X_n\)的数学期望\(E(X_n)\)关于\(n\)的表达式.

解答：

容易知道，$X_n $表示的是红球的个数，在取出放回的过程中红球只可能增加不可能减少。当袋子里面全都是红球的时候，之后的取出放回全都是在玩一袋子的\(8\)个红球.所以\(X_n\)可能的取值是\(3,4,5,6,7,8\).

如果当前有\(k(k\in [4,8])\)个红球，那么可以从上一次是\(k\)个红球或者是\(k-1\)个红球转移而来.那么：

\[P(X_n=k)=P(X_{n-1}=k) \cdot \frac{k}{8} + P(X_{n-1}=k-1) \cdot \frac{8-(k-1)}{8},(k\in [4,8]) \]

特别地：

\[P(X_n=3)=P(X_{n-1}=3) \cdot \frac{3}{8} \]

毕竟开始的时候只有\(3\)个红球，不可能从\(2\)个红球的状态转移而来.

我们根据期望的定义可以写出：

\[E(X_n)=\sum_{i=3}^{8}i \cdot P(X_n=i) \]

\[E(X_{n-1})=\sum_{i=3}^{8}i \cdot P(X_{n-1}=i) \]

根据所有相互独立的事件的概率和为\(1\)：

\[\sum_{i=3}^{8}P(X_{n-1}=i)=1 \]

可以猜测\(E(X_n)\)可以由\(E(X_{n-1})\)线性“拼凑”得到，于是待定系数，设：

\[E(X_n)=xE(X_{n-1})+y\qquad (*) \]

代入上式，让\((*)\)式只含有概率的线性和，解得\(x=\frac{7}{8},y=1\)

（这里可能说得比较抽象了， 意思就是让\((*)\)式变成只含有\(P_n(…)\)和\(P_{n-1}(…)\)啥的，此处省略一整张草稿纸，总之就是尝试用概率尝试拼凑期望的关系，让这个线性递推式成立）

则

\[E(X_n)=\frac{7}{8}E(X_{n-1})+1 \]

由于\(E(X_0)=3\)

则

\[E(X_n)=8-\frac{35}{8}(\frac{7}{8})^{n-1} \]

还没完。我们也可以换一种思路，利用差分值的期望来求原期望.

我们知道，\(X_{n+1}-X_n\)可能的取值是\(0,1\).

\[P(X_{n+1}-X_n=0)=\frac{X_n}{8} \]

\[P(X_{n+1}-X_n=1)=1- \frac{X_n}{8} \]

则期望：

\[E(X_{n+1}-X_n)=1- \frac{X_n}{8} \]

还是有个随机变量，再套一层\(E\).

\[E(E(X_{n+1}-X_n))=1- \frac{E(X_n)}{8} \]

套几层\(E\)都一样，不管是\(E(E(X))\)还是\(E(E(E(E(X))))\)都等于\(E(X)\).

所以

\[E(X_{n+1})-E(X_n)=1-\frac{1}{8}E(X_n) \]

得到递推式

\[E(X_n)=\frac{7}{8}E(X_{n-1})+1 \]

结果还是一样的.

---

e.x. EX

（Concrete Mathematics 8,47)*某些医生与某些物理学家合作，在最近发现了一对用一种特别方式进行繁殖的微生物。其中的雄性微生物称为双噬菌体\((diphage)\)，在它的表面上有两个接收器；而雌性微生物称为三噬菌体\((triphage)\),它有三个接收器：

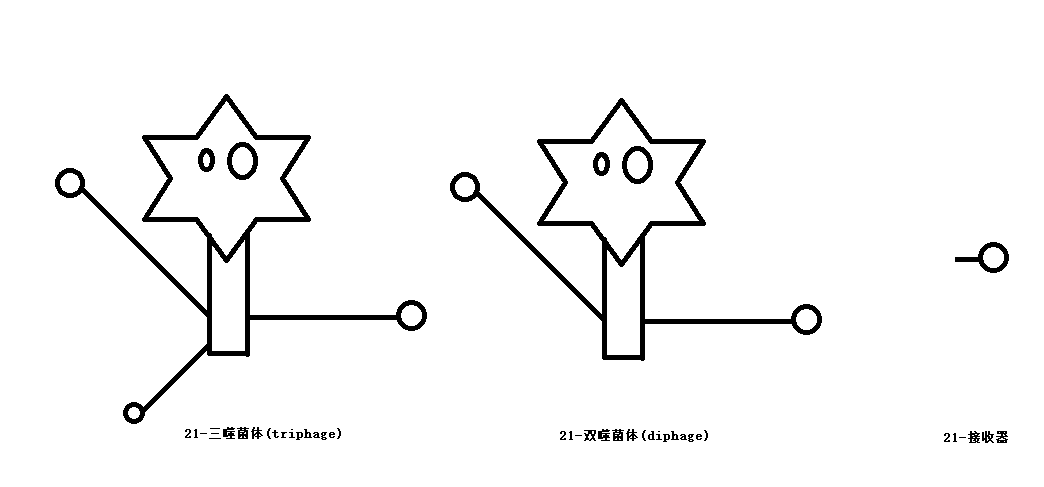
当双噬菌体以及三噬菌体的培养组织受到\(\psi\)粒子照射时，菌体上恰好有一个接收器吸收该粒子，每个接收器都是等可能的.如果这是一株双噬菌体的接收器，双噬菌体就转变成三噬菌体；如果这是三噬菌体的一个接收器，则该三噬菌体就分裂成为两株双噬菌体，这样一来，如果一个实验是从一株双噬菌体开始，第一个\(\psi\)粒子就将它变成一株三噬菌体，第二个粒子就将这株三噬菌体变成两株双噬菌体，而第三个\(\psi\)粒子就将这两株双噬菌体中的一个变成一株三噬菌体、第四个\(\psi\)粒子或者击中一林双磁菌体，或者击中一株三磁菌体，这样就得到两株三噬菌体（概率为\(p_1\)),或者得到三株双噬菌体(概率为\(p_2\)).现在从从单独一株双噬菌体开始并用单��的\(\psi\)粒子照射其培养组织\(n\)次，

\((I)\)求\(p_1,p_2\)的值；

\((II)\)求解下列问题：

\((i)\) 经过\(n (n\in \mathbb{N^*})\)次照射后，设随机变量\(X_n\)表示所存在的双噬菌体数目，设随机变量\(Y_n\)是第\(n+1\)个\(\psi\)粒子照射时，双噬菌体的增加量（可以为负）.求出\(Y_n\)的分布列，并求\(Y_n\)的数学期望\(E(Y_n)\)（结果含\(E(X_n)\)，\(E(X_n)\)是随机变量\(X_n\)的数学期望）.

\((ii)\)求出\(E(X_{n+1})\)和\(E(X_n)\)的递推式.

\((ii)^*\)求出\(E(X_n)(n>4)\)关于\(n\)的线性关系式.

解答：

\((I)\)\(p_1=\frac{2}{5},p_2=\frac{3}{5}\)，这是真的显然了.

\((II)\)

\((i)\)

首先考虑到在第\(n\)次照射后有\(n+2\)个一模一样的接收器,在第\(n+1\)此次照射的时，\(Y_n\)可能的取值有\(-1,+2\).

考虑命中一个双噬菌体使得双噬菌体个数\(-1\):

\[P(Y_n=-1)=\frac{2E(X_n)}{n+2} \]

再考虑命中一个三噬菌体让噬菌体个数\(+2\):

\[P(Y_n=+ 2)=1- \frac{2E(X_n)}{n+2} \]

那分布列就不难给出了.

\(Y_n\)	-1	+2
\(P(Y_n=k)\)	\(\frac{2E(X_n)}{n+2}\)	\(1-\frac{2E(X_n)}{n+2}\)

\[E(Y_n)=\frac{-6E(X_n)+2n+4}{n+2} \]

\((ii)\)

\[E(X_{n+1})=E(X_n)+E(Y_n)=E(X_n)+\frac{-6E(X_n)+2n+4}{n+2} \]

\[\Longrightarrow \quad (n+2)E(X_{n+1})=(n-4)E(X_n)+2n+4 \]

\(quite\quad easy\quad done.\)

\((ii)^*\)

这……emmm…有点棘手啊……我有学过咋求吗……

问题不大，我们可以找找规律.题目说了是线性关系嘛.

设\(E(X_n)=an+b\),又知道\(E(X_1)=0,E(X_2)=2\)

那么

\[0=a+b\\ 2=2a+b \]

要是你这么列式子解\(a,b\)你就裂开来.

题目说了\((n>4)\)的时候才有线性的性质，你就不能带入\(1,2,3,4\)去解你待定的系数.

规范操作首先利用递推式一个个算，算出\(E(X_5),E(X_6)\),然后利用之待定系数.

\(E(X_1)=0,E(X_2)=2,E(X_3)=1,E(X_4)=\frac{9}{5},E(X_5)=2,E(X_6)=\frac{16}{7}\)

\[2=5a+b \\ \frac{16}{7}=6a+b \]

解得\(a=\frac{2}{7},b=\frac{4}{7}\)

所以

\[E(X_n)=\frac{2n+7}{4},n>4. \]

这个时候回头用算出来的\(E(X_n)=\frac{2n+7}{4}\)尝试带入\(n=1,2,3,4\)发现都是跟事实\(E(X_1)=0,E(X_2)=2,E(X_3)=1,E(X_4)=\frac{9}{5}\)完全不符合的.所以千万要注意条件哦~

最后记得用数学归纳法证明\(E(X_n)=\frac{2n+7}{4},n>4.\)是成立的，这里就省略了（或者有空再写）.

事实上不给“线性”这个字眼也是能求的.只不过超纲了.（以后有空也许会补吧……）

未完待续。