LGOJ P1341 【无序字母对】

很STL的题解

想法似乎跟别人不大一样，我不喜欢在char和int之间换来换去，所以选择了

map<char, vector<int> > G;

至于字典序，这个sort一下就ok。

其他的就是常规dfs，特别注意一定要用栈记录倒序输出。不然只有一半分数。

似乎有人问道：为什么要用栈记录倒序输出？？
（dalao可以直接跳过本段）

我在这里简单而形象地解答一下：

举个例子：

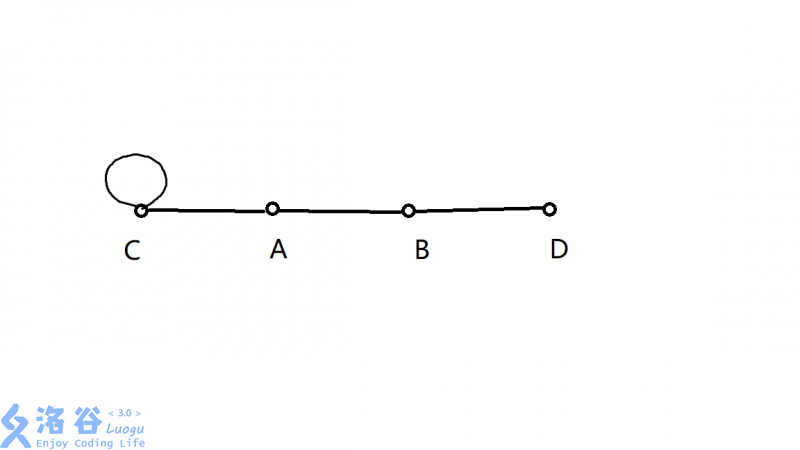
就这个图↑

显然，有且仅有两个点度数为奇，可以“一笔画”。我们在搜索的时候，如果这样写：

void dfs(char u)
{
	cout<<u;//先输出
	for (vector<int>::iterator it = G[u].begin(); it != G[u].end(); it++)
	{
		char now = *it;
		if (!vis[u][now])
		{
			vis[u][now] = 1;
			vis[now][u] = 1;
			dfs(now);
		}
	}
	
}

那就只有50分，因为对于上面所说的图该dfs的输出是：

CABDC

而正解是CCABD

这就要使用这种用栈记录倒序输出的方式了。

观察上面错误的输出，发现本该立即输出的C被滞后了，也就是说，这个C早该输出了。也就是说。我们应该保证一个点在输出之前确保之前的所有点已经输出过了。所以说输出的操作要放在最后，考虑到顺序问题应该倒序输出，堆个栈就行了。

下面是AC代码。
数据不够强，偷个懒就不判断图的连通性了。

#include "stdafx.h"
#include <bits/stdc++.h>
using namespace std;
map<char, vector<int> > G;
map<char, int> cnt;
bool vis[200][200];
stack<char> sta;
int n, ed;


void dfs(char u)
{
   for (vector<int>::iterator it = G[u].begin(); it != G[u].end(); it++)
   {
   	char now = *it;
   	if (!vis[u][now])
   	{
   		vis[u][now] = 1;
   		vis[now][u] = 1;
   		dfs(now);
   	}
   }
   sta.push(u);
}
bool cmp(char i, char j)
{
   return int(i) < int(j);
}
int main()
{
   cin >> n;
   bool flag = 0;
   char c = getchar(), q = 0;
   for (int i = 1; i <= n; i++)
   {
   	string s;
   	cin >> s;
   	G[s[0]].push_back(s[1]);
   	G[s[1]].push_back(s[0]);
   	cnt[s[0]]++;
   	cnt[s[1]]++;
   }
   int od = 0, x1 = 0, x2 = 0, c1 = 0, c2 = 0;
   for (map<char, int>::iterator it = cnt.begin(); it != cnt.end(); it++)
   {
       //保证一下字典序↓
   	sort(G[it->first].begin(), G[it->first].end(), cmp);
   	if (it->second % 2 != 0)
   	{
   		od++;//记录奇数点的个数
           //↓如果存在奇数点，那么这俩点就是路径的一始一末了
           //记录下来
   		if (x1)x2 = it->second, c2 = it->first;
   		else x1 = it->second, c1 = it->first;
   	}
   }
   if (od != 2 && od != 0)
   {
   	cout << "No Solution";
   	return 0;
   }
   else
   {
   	char minst = 'z';
   	for (map<char, vector<int> >::iterator it = G.begin(); it != G.end(); it++)
   	{
   		if (minst > it->first)minst = it->first;
   	}
   	if (od == 2)
   	{
   		minst = min(c1, c2);
   	}
   	dfs(minst);//搜
   }
   while (!sta.empty())
   {
   	cout << sta.top();
   	sta.pop();
   }
   return 0;
}