算法设计与分析2_Growth of functions(渐进界)

与MIT算法导论教材对应关系
Chapter 3. 函数的渐进增长

Topics:
• Growth of functions
• O/o/Θ/Ω/ω notations

渐近表示法

算法的渐近时间定义为一个函数，定义域为自然数集合N={0,1,2,...}(∵n表示Size)。但有时也将其扩展到实数或限制到自然数的某子集上。(P25)

\(\theta\) 渐进确界 (\(\theta\)-notation)🌟

考试:渐进确界 \(\theta\)的证明（上课讲过）

Θ(g(n))={f(n)：存在正整数c1,c2,n0,并且对于所有n≥n0,满足0≤c1g(n)≤f(n)≤c2g(n)}

Def：给定一个函数g(n)， \(\theta (g(n))\)表示一个函数的集合：

• 即 \(f(n) = \theta(g(n))\) 表示存在正常数\(c_1\), \(c_2\)及足够大的n，使得f(n)夹在\(c_1g(n)\)和\(c_2g(n)\)之间
  

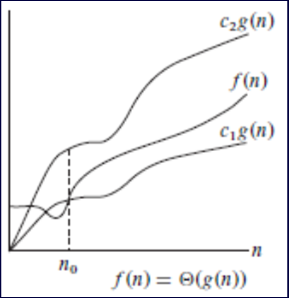
大Θ的数学定义(渐进紧致界) 与\(\theta\)无区别

我们称g(n)是f(n)的一个渐进紧致(确)界(asymptotically tight bound)

意义：

• 对所有的n≥n0，函数f(n)在一个常数因子范围内等于g(n)
• g(n)是f(n)的一个渐近紧致(确)界，即g(n)是f(n)的
  渐近上界和渐近下界.

f(n)—算法的计算时间
g(n)—算法时间的数量级
不同的输入实例，一个算法的计算时间f(n)不一定相同，故算法的计算时间应该是一个函数集合

Note： Θ定义中要求f(n)和g(n)是渐近非负的(n足够大时函数值非负)否则\(\theta (g(n))\) 是空集

记号：
\(\theta (1)\)表示算法的运行时间与问题规模n无关，亦可理解为常值函数(任何常数是0次多项式)

🌟考试:渐进确界θ的证明

例1

例1(Page 27 in textbook)：
\(T(n)=an^2+bn+c (a>0)\)
那么\(T(n) = \theta(n^2)\)
证明：

取\(c_1 = \frac{a}{4}\)，\(c_2 = 7\frac{a}{4}\)，\(n_0 = 2\max(\frac{|b|}{a}, \sqrt{\frac{|c|}{a}})\)
那么对于所有的\(n>n_0\)，有\(0<= c_1n^2 <= T(n) <= c_2n^2\) 成立

例2

证明\(an^3+bn^2+cn+d = \theta (n^3)\) \(a>0\)

下界分析
\(f(n) \geq \frac{1}{2}an^3 + \left( \frac{1}{2}an^3 + bn^2 + cn + d \right)\)。

$
f(n) \geq \frac{1}{2}an^3 + \left( \frac{1}{2}an^3 - |b|n^2 - |c|n - |d| \right)
$

$
f(n) \geq \frac{1}{2}an^3 + \left( \frac{an^3}{2} - |b|n^2 - |c|n^2 - |d|n^2 \right)
$
$
f(n) \geq \frac{1}{2}an^3 + \left( \frac{an}{2} - |b| - |c| - |d| \right)n^2 \quad (n \geq 1)
$

选取 \(n_0\)： $ n_0 = \lceil \frac{2(|b| + |c| + |d|)}{a} + 1 \rceil$

\(f(n) \geq \frac{1}{2}an^3 + \left( \frac{a}{2} \cdot \frac{2(|b| + |c| + |d|)}{a} + 1 - |b| - |c| - |d| \right) n^2\)
\(f(n) \geq \frac{1}{2}an^3 +\frac{1}{2}an^2\)
\(f(n) \geq \frac{1}{2}an^3\)

上界分析：
$ f(n) \leq an^3 + |b|n^2 + |c|n + |d|$
\(f(n) \leq (a + |b|/n + |c|/n^2 + |d|/n^3)n^3\)
\(f(n) \leq (a + |b| + |c| + |d|)n^3\)

选取 \(n_0\)： $ n_0 = \lceil 2(|b| + |c| + |d|)/a + 1 \rceil$
对于 \(n > n_0\)，有 \(C_1 = \frac{1}{2}a\)，\(C_2 = a + |b| + |c| + |d|\)，使得\(C_1n^3 \leq f(n) \leq C_2n^3\)

• 因此，\(f(n) = \Theta(n^3)\)。

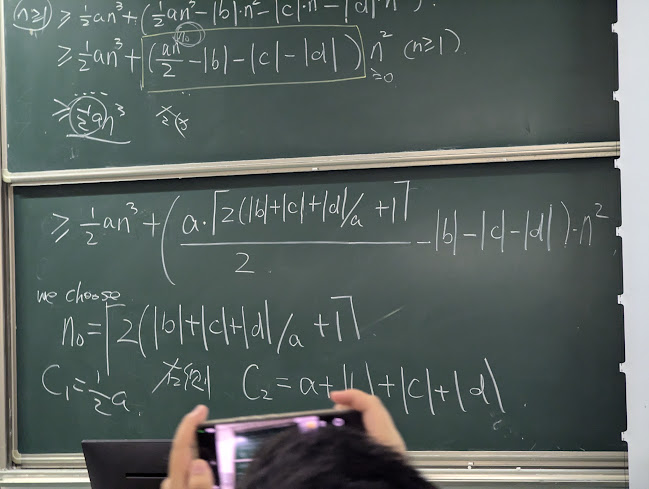
例3

证明函数 \(6n\lg n + \sqrt{n}\lg^2 n = \Theta(n\lg n)\)

解：
若上式成立,则存在正常量\(c_1\), \(c_2\), 和\(n_0\), 使得对所有\(n≥n_0\)，有

\[0 \leq c_1n\lg n \leq f(n) \leq c_2n\lg n。 \]

(1) 下界分析：
当 n >= 1 时, 显然 \(\sqrt{n}\lg^2 n \geq 0\)

$f(n) = 6n\lg n + \sqrt{n}\lg^2 n \geq 6n\lg n $

所以可取 \(c_1 = 6\)。

(2) 上界分析：
当 n >= 2 时,

\(f(n) = 6n\lg n + \sqrt{n}\lg^2 n \leq 6n\lg n + n\lg n = 7n\lg n\)

所以可取 \(c_2 = 7\)。

综上
取 \(n_0 = max\{1,2\} = 1\), \(C_1 = 6\)，\(C_2 = 7\)使得\(6n\lg n \leq f(n) \leq 7n\lg n\)成立
所以 \(f(n) = \Theta(n\ln n)\)

例4

例:证明 \(1/2 * n(n - 1) \in \Theta(n ^ 2)\)

解
若上式成立,则存在正常量\(c_1\), \(c_2\), 和\(n_0\), 使得对所有\(n≥n_0\)，有

\[0 <= c_{1} * n ^ 2 <= 1/2 * n(n - 1) <= c_{2} * n ^ 2 \]

当 n >= 0 时, \(1/2 * n(n - 1) = 1/2 * n ^ 2 - 1/2 * n <= 1/2 * n ^ 2\) 所以可取 \(c_{2} = 1/2\)

当 n >= 2 时 \(1/2 * n(n - 1) = 1/2 * n ^ 2 - 1/2 * n >= 1/2 * n ^ 2 - 1/2 * n * 1/2 * n >= 1/4 * n ^ 2\) 所以可取 \(c_{1} = 1/4\)
综上,取 \(n_{0} = 2\) \(c_{1} = 1/4\) \(c_{2} = 1/2\) 有 \(0 <= c_{1} * n ^ 2 <= 1/2 * n(n - 1) <= c_{2} * n ^ 2\)

Asymptotic Notation in Equations
Used to replace functions of lower-order terms to simplify equations/expressions.

For example
\(4n3 + 3n2 + 2n + 1 = 4n3 + 3n2 + Θ(n)= 4n3 + Θ(n2) = Θ(n3)\)

Or we can do the following: \(4n3 + 3n2 + 2n + 1 = 4n3 +f(n2)\), where \(f(n2)\) simplifies the equation

课本P27，直觉上……

O 渐近上界 (notation)

O(g(n))={f(n):存在正整数c,n0,并且对于所有n≥n0满足0≤f(n)≤cg(n)}
Def:

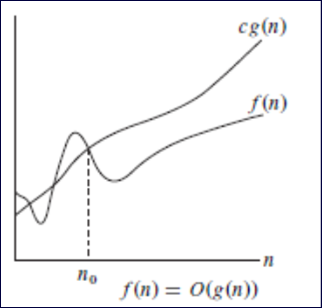
Θ是一个比O记号更强的概念;

g(n)是f(n)的一个渐进上界(Asymptotically upper bound),限制算法最坏情况运行时间;

Note：
O描述上界，当用于界定一个最坏运行时间时，蕴含着该算法在任意输入上的运行时间都囿于此界
\(\theta\)则不然，一个算法的最坏运行时间是\(\theta ( g(n) )\)，并非蕴含着该算法对每个输入实例的运行时间均囿于\(\theta ( g(n) )\)

例

Example

1/3n²-3n ∈ O(n²) because 1/3n² - 3n ≤ cn² if c ≥ 1/3 - 3/n which holds for c = 1/3 and n > 1

k₁n² + k₂n + k₃ ∈ O(n²) because k₁n² + k₂n + k₃ ≤ (k₁ + |k₂| + |k₃|)n² and for c > k₁ + |k₂| + |k₃| and n ≥ 1 ,

k₁n² + k₂n + k₃ ≤ cn²

k₁n² + k₂n + k₃ ∈ O(n³) as k₁n² + k₂n + k₃ ≤ (k₁ + |k₂| + |k₃|)n³

解释和补充说明：

大O符号用于描述算法的增长率或复杂性，尤其是在输入大小（通常用 n 表示）变得非常大时。它关注的是算法运行时间或空间需求的 上限。

• 1/3n²-3n ∈ O(n²)：这意味着表达式 1/3n² - 3n 的增长速度 最多 与 n² 相同。当 n 变得非常大时，-3n 项变得相对不重要，因此主要项是 1/3n²。可以选择一个常数 c（例如 1/3），使得对于所有足够大的 n 值，1/3n² - 3n ≤ cn² 成立。

• k₁n² + k₂n + k₃ ∈ O(n²)：这是一个更通用的例子，表明任何二次多项式都属于 O(n²)。常数 k₁, k₂ 和 k₃ 可以是任何值。关键在于，当 n 变得非常大时，n² 项支配着增长，而线性项（k₂n）和常数项（k₃）变得不重要。通过选择足够大的 c 值（例如 k₁ + |k₂| + |k₃|），可以确保 k₁n² + k₂n + k₃ ≤ cn² 对于所有 n ≥ 1 成立。这里使用绝对值 |k₂| 和 |k₃| 是为了确保不等式即使在 k₂ 和 k₃ 是负数时也成立。

• k₁n² + k₂n + k₃ ∈ O(n³)：这个例子说明，如果一个函数是 O(n²)，那么它也 必然 是 O(n³)。因为 n³ 的增长速度比 n² 快。如果一个函数受 n² 的限制，那么它也 一定 受 n³ 的限制。虽然这个陈述是正确的，但通常我们使用 最紧 的上限。也就是说，我们更倾向于说 k₁n² + k₂n + k₃ ∈ O(n²)，而不是 O(n³)，因为它提供了更精确的增长率描述。

当说算法的运行时间上界是\(O(n^2)\)往往是指其最坏运行时间，无须修饰语，对那些最好、最坏、平均时间数量级不同者均成立，而Θ则要分开表达、加修饰语。

Ω 渐近下界 (lower bound)

Ω(g(n))={f(n):存在正整数c,n0,并且对于所有n≥n0满足0≤cg(n)≤f(n)}

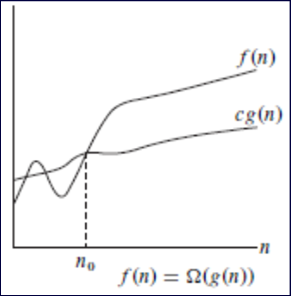
当用\(Ω\)来界定一个算法的最好情况下的运行时间时，蕴含着该算法在任意输入上的运行时间都囿于此界

例：
 插入排序的下界是\(Ω(n)\)，对任何实例成立(即插入排序
的最好运行时间是\(Ω(n)\))
∵ \(n=Ω(n)\) \(n^2=Ω(n)\)

方程中的渐近记号

例子：基于比较的排序时间下界是

lgn! = nlgn - 1.44n + O(lgn)
“可消去不必要的细节，突出主项的常数因子等。”

o 非渐近紧确上界 (Littel-o)

o(g(n))={f(n):存在正整数c,n0,并且对于所有n≥n0满足0≤cf(n)<g(n)}

大O记号表示的渐近上界可以是渐近紧致的，也可以是
渐近非紧界
小O记号只能用来表示——函数的渐近非紧致上界

例 2n=o(n²) 但 2n²≠o(n²)。

• 2n=o(n²)：这意味着当 n 趋于无穷大时，2n 相对于 n² 是 可忽略的。
• 2n²≠o(n²)：这意味着 2n² 相对于 n² 不是 可忽略的。

直观上，当 n→∞，f(n)相对于 g(n)是可忽略的

直观上，当n趋于无穷，f(n)相对于g(n)是可忽略的
**即：f(n)=o(g(n)) 蕴含着 \(\lim_{n \to \infty} \frac{f(n)}{g(n)} = 0\)

或说 f 和 g 数量级不同，否则不可能对于任意常数 c，都有 cg(n) 严格大于 f(n)

ω 非渐近紧确下界 (Littel-omega)

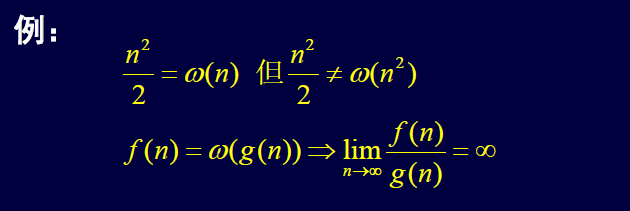
函数间比较

许多实数的关系性质可用(引申)到渐近比较，下面假定f(n)和g(n)是渐近正的

1. 传递性(对于五种渐进记号均适用)

2. 自反性(渐近非紧界无自反性)

3. 对称性(仅对渐进紧确界成立)//大O与大Ω对调时， f、g对称

4. 转置对称性// g是f的非紧上界等价于f是g的非紧下界

基本运算规则

1. \(O(f(n)) + O(g(n)) = O(\max(f(n), g(n)))\)：
   这个规则表示两个函数的和的复杂度等于它们中较大者复杂度的上界。但是，这个规则的表述似乎有误，正确的表述应该是 \(O(f(n)) + O(g(n)) = O(f(n) + g(n))\)，这意味着两个函数的和的复杂度是它们各自复杂度的和。

2. \(O(f(n)) + O(g(n)) = O(f(n) + g(n))\)：
   这个规则是正确的，它表示两个函数的复杂度之和等于它们和的复杂度。

3. \(O(f(n)) \cdot O(g(n)) = O(f(n) \cdot g(n))\)：
   这个规则表示两个函数的乘积的复杂度等于它们各自复杂度的乘积。

4. \(O(cf(n)) = O(f(n))\)：
   这个规则表示，如果一个函数乘以一个常数，它的复杂度不会改变。常数因子在大O符号中是可以忽略的。

5. \(g(n) = O(f(n)) \Rightarrow O(f(n)) + O(g(n)) = O(f(n))\)：
   这个规则表示，如果 \(g(n)\) 的复杂度是 \(f(n)\) 的上界，那么 \(f(n)\) 和 \(g(n)\) 的和的复杂度等于 \(f(n)\) 的复杂度。这是因为 \(g(n)\) 已经被 \(f(n)\) 的复杂度所包含。

并非所有函数都是渐近可比较的
例如：函数 \(n\) 和 \(n^{1+\sin n}\) 之间是无法渐近比较的。

1. 当 \(\sin n\) 接近 -1 时，\(1 + \sin n\) 接近 0，这意味着 \(n^{1+\sin n}\) 接近 \(n^0 = 1\)，即 \(O(1)\)。

2. 当 \(\sin n\) 接近 1 时，\(1 + \sin n\) 接近 2，这意味着 \(n^{1+\sin n}\) 接近 \(n^2\)，即 \(O(n^2)\)。

因此，函数 \(n^{1+\sin n}\) 的增长速度会随着 \(\sin n\) 的值在 0 到 2 之间变化，这意味着它在 \(O(1)\) 和 \(O(n^2)\) 之间波动。

在算法复杂度分析中，我们通常寻找的是函数增长的上界，以便了解最坏情况下的性能。对于 \(n^{1+\sin n}\)，虽然它在 \(O(1)\) 和 \(O(n^2)\) 之间波动，但在最坏的情况下，它的增长速度可以被 \(O(n^2)\) 所界定。然而，这种界定并不精确反映函数在所有情况下的行为

Asymptotic order of growth

A way of comparing functions that ignores constant
factors and small input sizes
O(g(n)): class of functions f(n) that grow no faster than g(n)
Θ(g(n)): class of functions f(n) that grow at same rate as
g(n)
Ω(g(n)): class of functions f(n) that grow at least as fast as
g(n)