算法设计与分析3 NP, NPC, NP-hard

NP问题

NP问题

给定一个解，多项式时间内验证是不是正解

NP 完全问题

问题是 NP 完全的，这意味着：

• 该问题的解可以在多项式时间内验证。
• 目前没有已知的多项式时间算法可以解决所有实例。

规约（必考）

核心目的：证明两个问题是同等难度的问题。
一般性问题是NPC，特殊的问题也是NPC

三种规约策略

简单等价规约

从特殊到一般

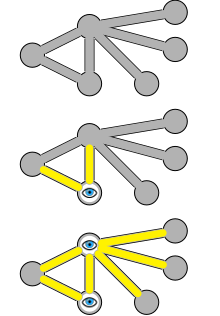
顶点覆盖（Vertex cover）
图的顶点覆盖（有时是节点覆盖）是一组顶点的集合，使得图的每个边缘至少与集合中的一个顶点相连接。

集合覆盖问题

集合覆盖（Set Cover）是一个经典的组合优化问题，通常表述为：给定一个集合 $U$ 和一组子集 $S_1, S_2, \ldots, S_m$，求最小的子集集合 $S' \subseteq {S_1, S_2, \ldots, S_m}$，使得 $S'$ 的并集覆盖了整个集合 $U$。

$ 例子

假设有一个集合 $U = \{1, 2, 3, 4, 5\}$，以及以下子集：

• $S_1 = {1, 2}$
• $S_2 = {2, 3}$
• $S_3 = {3, 4}$
• $S_4 = {4, 5}$

在这个例子中，集合 ${S_1, S_2, S_3, S_4}$ 中最小的子集集合可能是 ${S_2, S_4}$，因为它们的并集 ${2, 3, 4, 5}$ 覆盖了 $U$。

将集合$S_1, S_2, \ldots, S_m$，类比到 顶点覆盖问题的V， 那么集合中的元素就类比到 图中的 边。
问题就

通过编码Encoding with gadgets

CNF-SAT 问题

，即合取范式满足性问题，是计算机科学领域的一个基础性问题，也是 NP 完全问题的典型代表。 它的本质在于判断一个以合取范式 (CNF) 表示的布尔公式是否存在一种变量赋值，使得该公式的取值为真。

基本概念:

• 布尔变量: 只能取真 (true) 或假 (false) 两种值。
• 文字: 一个布尔变量，或者它的否定 (negation)。例如，A 是一个文字，¬A 也是一个文字。
• 子句: 由若干个文字通过“或” (∨, 逻辑或) 连接而成。例如，(A ∨ ¬B ∨ C) 是一个子句。
• 合取范式 (CNF): 由若干个子句通过“与” (∧, 逻辑与) 连接而成。例如，(A ∨ ¬B) ∧ (¬A ∨ C) ∧ (B ∨ C) 是一个 CNF 公式。

CNF-SAT 问题就是：
给定一个 CNF 公式，判断是否存在一种对其中布尔变量的真值赋值，使得整个公式的取值为真。如果存在这样的赋值，则称该 CNF 公式是可满足的 (satisfiable)，否则称它是不可满足的 (unsatisfiable)。

3-CNF 问题

是 CNF-SAT 问题的一个特殊情况，其中每个子句都恰好包含三个文字。

给定一个 3-CNF 公式（即每个子句都包含三个文字的 CNF 公式），判断是否存在对其中布尔变量的真值赋值，使得整个公式的取值为真。

例子:

(A ∨ ¬B ∨ C) ∧ (¬A ∨ B ∨ ¬C) 是一个 3-CNF 公式。

3-CNF-SAT规约 independent-Set

图片来自

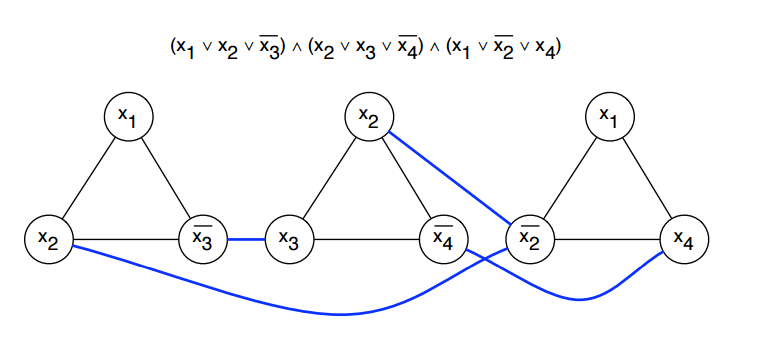
子句内部的三角形表示 只能选一个元素

转换成size为k的独立集问题（k为子句数量）

例题

SubSet sum problem $<=_p$ Partition Problem

Subset Sun: Given a set of integers. T={t1,t2,..;tn} • is there a non-empty subset whose sum is k.

Partition : (Number Partitioning) is the task of deciding whether a given Set W of positive integers can be partitioned into two subsets W. & W₂, such that the sum of the numbers Vi equal's to the sum of W₂

• 子集 Sun：给定一组整数。T={t1,t2,..;tn} • 是否存在一个非空子集，其和为 k。

• 分割：（数字分割）是决定给定的正整数集合 W 是否可以分成两个子集 W1 和 W2，使得数字 W1 的总和等于 W2 的总和
  https://www.youtube.com/watch?v=_mpVTPBepjY

子集求和问题定义：给定一个整数集合 $S$ 和一个目标值 $T$，问是否存在一个子集 $S' \subseteq S$，使得 $S'$ 中元素的和等于 $T$。

数字分割问题定义：给定一个整数集合 $S$，问是否可以将其分割成两个子集 $S_1$ 和 $S_2$，使得 $S_1$ 和 $S_2$ 的元素和相等。

可以通过以下步骤将数字分割问题规约到子集求和问题：

1. 输入转换：给定一个集合 $S$，计算集合中所有元素的和 $\text{sum}(S)$。

2. 目标值计算：如果 $\text{sum}(S)$ 为奇数，则直接返回“不可分割”，因为无法将奇数分成两个相等的整数。如果 $\text{sum}(S)$ 为偶数，定义目标值为 $T = \frac{\text{sum}(S)}{2}$。

3. 子集求和实例：然后，将问题转化为子集求和问题：问是否存在子集 $S' \subseteq S$，使得 $S'$ 中元素的和等于 $T$。

反向规约 同样地，也可以将子集求和问题规约到数字分割问题：

1. 输入转换：给定一个集合 $S$ 和目标值 $T$。

2. 集合构造：在数字分割问题中，构造一个新的集合 $S' = S \cup \{T\}$。

3. 判断分割：然后判断是否可以将 $S'$ 分成两个子集，使得两个子集的和相等。如果存在 $S'$ 的一个子集和等于 $T$，则可以将 $S$ 分成两个和相等的部分。

np完全问题证明实例

证明 哈密顿回路 <=p TSP

哈密顿环问题

证书：特定解的解决方案

哈密顿环问题（Hamiltonian Cycle Problem）是图论中的一个经典问题，属于 NP 完全问题。以下是该问题的详细介绍。

问题描述

定义：给定一个无向图 $G = (V, E)$，哈密顿环问题的目标是判断是否存在一条哈密顿环（Hamiltonian cycle），即一条经过图中每个顶点恰好一次并最终回到起始顶点的闭合路径。

例子 考虑一个简单的无向图：

   A
  / \
 B---C
  \ /
   D

在这个图中，存在的哈密顿环可以是 $A \to B \to D \to C \to A$。

旅行商问题（Traveling Salesman Problem, TSP）

问题描述

定义：给定一组城市及其之间的距离（或成本），旅行商问题的目标是找到一条最短的路线，使得旅行商从一个城市出发，经过所有其他城市恰好一次，并最终返回到起始城市。

数学形式

给定一个完全有向带权图 $G = (V, E)$，其中顶点集 $V$ 代表城市，边集 $E$ 代表城市间的距离或成本。问题可以表述为：

• 找到一个哈密顿环，使得该环的总边权最小。

例子

假设有 4 个城市 A, B, C, D，它们之间的距离如下：

	A	B	C	D
A	0	10	15	20
B	10	0	35	25
C	15	35	0	30
D	20	25	30	0

在这个例子中，旅行商的最短路线可能是 A → B → D → C → A。

求解

总结（必看）

P、NP、NPC、NP-hard

P：问题存在一个多项式时间的求解算法。
NP：问题存在一个多项式时间的验证算法（在多项式时间内验证一个给定的解是否正确）

NPC：对于一个(判定性)问题q，满足以下两个条件，那么它就是NPC问题（NP-完全的/NP-complete）：

1. q属于NP
2. NP中任一问题均可多项式时间多一归约到q（即任何一个NP问题都可以在多项式时间内转化为该问题的一个实例）。

NP-hard (NP难)：如果一个问题满足所有NP问题都可以规约到它，但不一定属于NP类，那么它就是NP-hard问题。

四者的关系

---

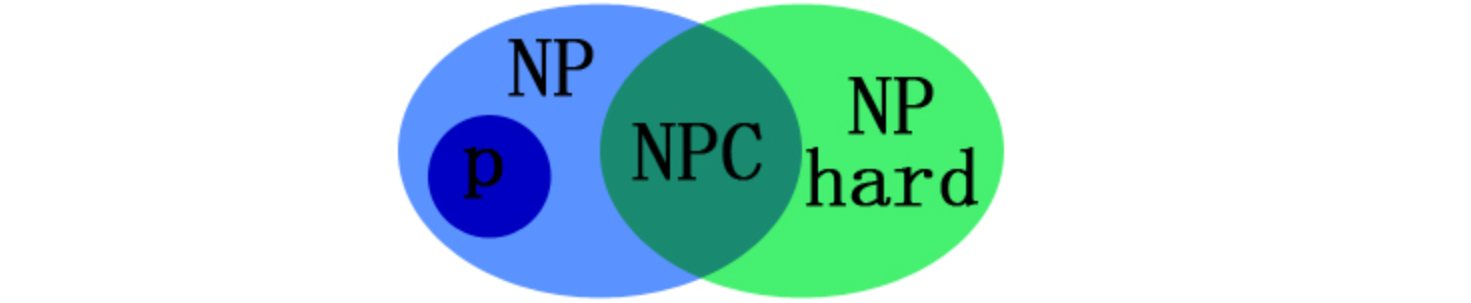
1. P (Polynomial Time, 多项式时间)

• 定义： 如果一个问题存在一个求解算法，其时间复杂度是输入规模的多项式函数，那么这个问题就属于P类问题。
• 例子： 数组排序（例如归并排序、快速排序）、线性搜索、图的广度优先搜索（BFS）和深度优先搜索（DFS）等。
• 特点： P类问题通常被认为是“易解的”，因为它们可以在合理的时间内解决，即使输入规模很大。

2. NP (Non-deterministic Polynomial Time, 非确定性多项式时间)

• 定义： 如果一个问题存在一个验证算法，可以在多项式时间内验证一个给定的解是否正确，那么这个问题就属于NP类问题。
• 关键： NP问题强调的是“验证”的效率，而不是“求解”的效率。
• 例子：
  • 旅行商问题 (TSP)： 给定一系列城市和它们之间的距离，是否存在一条访问每个城市恰好一次并返回起点的路径，其总长度不超过某个给定的值？给定一条路径，我们可以在多项式时间内验证其是否满足要求。
  • 哈密顿回路问题 (Hamiltonian Cycle Problem)： 给定一个图，是否存在一条路径，该路径访问每个顶点恰好一次并返回起点？给定一条路径，我们可以在多项式时间内验证其是否是哈密顿回路。
  • 子集和问题 (Subset Sum Problem)： 给定一个整数集合和一个目标值，是否存在一个子集，其元素之和等于目标值？给定一个子集，我们可以在多项式时间内计算其元素之和并与目标值进行比较。
• 重要说明：
  • NP问题不一定存在多项式时间的求解算法。我们只知道如果给定一个解，我们可以高效地验证它。
  • 所有P类问题都是NP问题（因为如果一个问题可以在多项式时间内求解，那么一定也可以在多项式时间内验证解的正确性），即P⊆NP。

3. NPC (NP-Complete, NP完全)

• 定义： 如果一个问题满足以下两个条件，那么它就是NPC问题：
  1. 它是NP问题。
  2. 所有NP问题都可以规约到它（即任何一个NP问题都可以在多项式时间内转化为该问题的一个实例）。
• 规约 (Reduction)： 将问题A规约到问题B意味着，如果存在一个解决问题B的有效算法，那么也可以使用该算法来解决问题A。
• 重要意义： NPC问题是NP问题中最“难”的问题。如果任何一个NPC问题能够找到多项式时间的解法，那么所有NP问题都将可以在多项式时间内解决，即P=NP。
• 例子： 旅行商问题 (TSP)、哈密顿回路问题、子集和问题、布尔可满足性问题 (SAT) 等。

4. NP-hard (NP难)

• 定义： 如果一个问题满足所有NP问题都可以规约到它，但不一定属于NP类，那么它就是NP-hard问题。
• 关键区别： NP-hard问题不要求自身是NP问题。也就是说，NP-hard问题可能无法在多项式时间内验证一个给定的解。
• 例子： 停机问题 (Halting Problem) 是一个经典的NP-hard问题，但它不是NP问题。
• 重要说明： NPC问题一定是NP-hard问题，但NP-hard问题不一定是NPC问题。

总结

• P问题是可以在多项式时间内解决的问题。
• NP问题是可以在多项式时间内验证解的问题。
• NPC问题是NP问题中最难的问题，所有NP问题都可以规约到它。
• NP-hard问题比NPC问题更广泛，它不要求自身是NP问题。

其他

■ NP-完全性理论的局限性

易解问题（P问题）:可多项式时间内求解的问/题

难解问题（NP问题）:需超多项式时间求解的问题

NP-完全性理论既没有找到第二类问题的多项式时间的算法,也没有证明这样的算法就不存在,而是证明了这类 问题计算难度之等价性(彼此间困难程度相当)。因此,NPC具有如下性质:若其中1个问题多项式可解当且仅当 其他所有NPC问题亦多项式可解

■难解问题与易解问题之相似性

1. 最短/最长简单路径
   单源最短路径问题:对有向图G,时间O(VE), P问题
   两点间最长路径:NPC问题,即使所有边上权为1

2. 欧拉环/哈密尔顿圈(G为无向图或有向图)
   欧拉环:G中有通过每条边恰好一次的环? P,多项式时间可解
   哈氏圈:G中有通过每个顶点恰好1次的圈? NPC

关于归约总结(续)
3. (非常有用!!!)寻找特例:
■某些NPC恰恰是其他NPC的特例,比如partition problem 是 knapsack problem的特例,如果你知道问题X是NPC,并且X是Y的特例,那么Y必定 也是NPC,为什么?
因为Y比X更具一般性,问题Y至少与X一样难!!!

4. 寻找合适的归约源:
   ■ 有的时候,我们会选择跨域归约策略,3-CNF可满足性问题是一个进行跨域
   归约合适的归约源。既可以归约到团问题(Graph)也可以归约到子集和
   (knapsack branch);
   ■ 在图问题中,如果需要选择部分图,且无需考虑顶点顺序,那么顶点覆盖问 题通常是一个合适的归约源