【JVM】-NO.110.JVM.1 -【JDK11 HashMap详解】
Style:Mac
Series:Java
Since:2018-09-10
End:2018-09-10
Total Hours:1
Degree Of Diffculty:5
Degree Of Mastery:5
Practical Level:5
Desired Goal:5
Archieve Goal:3
Gerneral Evaluation:3
Writer:kingdelee
Related Links:
http://www.cnblogs.com/kingdelee/
http://www.runoob.com/java/java-operators.html
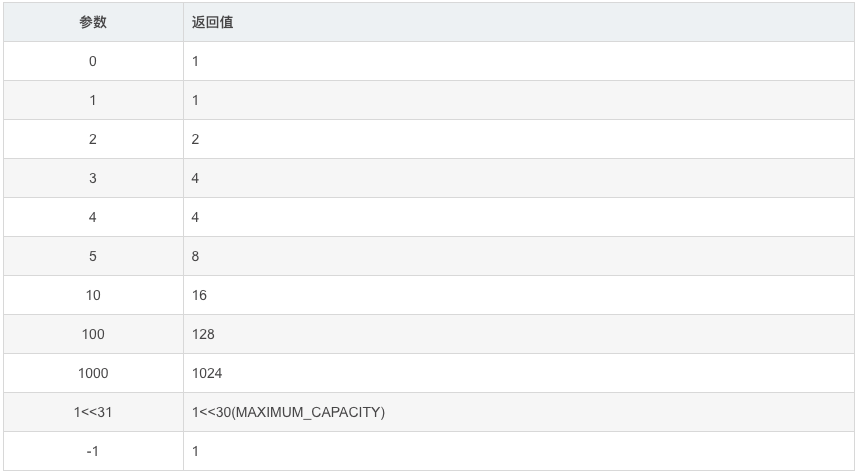
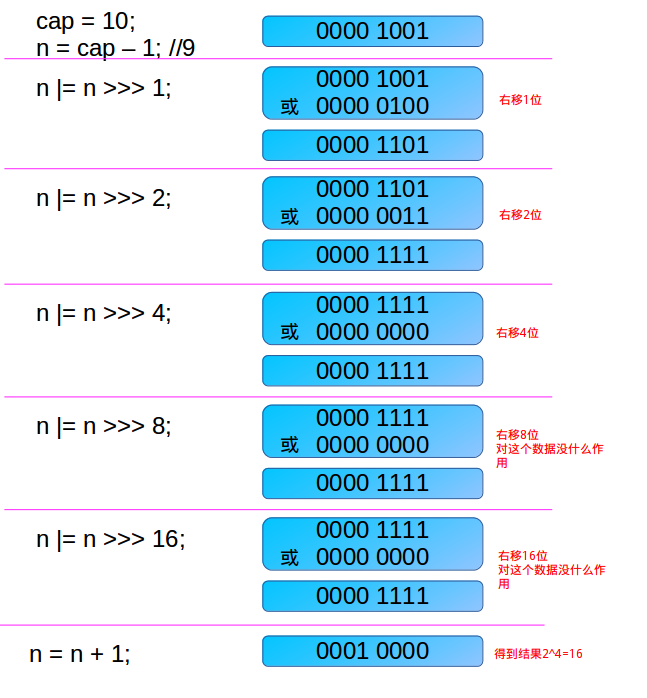
1.传入自定义容量的值,会经过下面算法进行计算,最终生成一个结果为 稍稍大于传入值且小于 2的n次幂的数,以下这个是jdk10的
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
jdk11的是:
static final int tableSizeFor(int cap) {
int n = -1 >>> Integer.numberOfLeadingZeros(cap - 1);
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
在Integer里边
@HotSpotIntrinsicCandidate
public static int numberOfLeadingZeros(int i) {
// HD, Count leading 0's
if (i <= 0)
return i == 0 ? 32 : 0;
int n = 31;
if (i >= 1 << 16) { n -= 16; i >>>= 16; }
if (i >= 1 << 8) { n -= 8; i >>>= 8; }
if (i >= 1 << 4) { n -= 4; i >>>= 4; }
if (i >= 1 << 2) { n -= 2; i >>>= 2; }
return n - (i >>> 1);
}
2.关键词
hash
2.1 hash算法
执行put时
private int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
putval
if ((p = tab[i = (n - 1) & hash]) == null) // i: (16-1) & 10 = 10,未存在节点的情况下,让新节点P指向数组节点tab中的hash后的节点,创建节点数组;已经存在节点时不再进来;n是tab的长度
{
logger.info("创建一个新节点,tab["+i+"]指向这个节点" + "hash:" + hash + ",value:" + value);
tab[i] = newNode(hash, key, value, null); // 仅在p节点为空的情况下,创建刚刚新节点指向hash后为空的节点的位置
}
以上完成了,将创建的新节点,赋给 横向的数组tab中的某个槽位,槽位
解释hash算法:
hash = (h = key.hashCode()) ^ (h >>> 16) 00000000000000000000000001100100 100的2进制 00000000000000000000000000000000 100右移16位,明显为0 00000000000000000000000001100100 ^异或运算,只要a != b 就为1,否则为0;即结果仍为a (n-1) & hash,n是tab的长度,初始为16 即 15 & hash 00000000000000000000000000001111 15的2进制 00000000000000000000000001100100 hash为100时的2进制 00000000000000000000000000000100 &与运算,a=b=1 就为1,否则为0;结果是4 00000000000000000000000000001111 15的2进制 00000000000000000000000001100101 hash为101时的2进制 00000000000000000000000000000101 &与运算,a=b=1 就为1,否则为0;结果是5 00000000000000000000000000001111 15的2进制 00000000000000000000000001100110 hash为102时的2进制 00000000000000000000000000000110 &与运算,a=b=1 就为1,否则为0;结果是6 (正顺序定义为从右往左数,首位为0)发现,a的第4位为0,即无论b是什么数,第4位往后是什么都无意义与运算结果总是为0. 所以只看前3位,即结果一定是在a范围内的。 结果似乎是散列无碰撞的 如果长度是17呢? 即 16 & hash 00000000000000000000000000010000 16的2进制 00000000000000000000000001100100 hash为100时的2进制 00000000000000000000000000000000 &与运算,a=b=1 就为1,否则为0;结果是0 00000000000000000000000000000000 16的2进制 00000000000000000000000001100101 hash为101时的2进制 00000000000000000000000000000000 &与运算,a=b=1 就为1,否则为0;结果是0 00000000000000000000000000000000 16的2进制 00000000000000000000000001100110 hash为102时的2进制 00000000000000000000000000000000 &与运算,a=b=1 就为1,否则为0;结果是0 结果都是0,都往一个坑里跳了
看一下代码,如果有100-200的hash值,在长度为16和17的情况下的槽位输出
int len = 16;
List<Integer> list = new ArrayList<>();
List<Integer> resultList = new ArrayList<>();
for (int i = 100; i < 200; i++) {
list.add(i);
}
for (Integer i : list) {
resultList.add((i ^ (i >> 16)) & (len - 1));
}
System.out.println(resultList.toString());
输出:
[4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7]
当 len = 17 时
输出:
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 0, 0, 0, 0, 0, 0, 0, 0]
1.对于 hash()的算法中,(h ^ h>>16)
发现,只要是在hashcode的位数小于等于16位,右移后都会被清空,即h>>6结果总是为0。
对于任意一个h^0,结果都是h
明显发现17时,这个算法的散列能力很差,绝大多数的数仅分布在两个不一样的槽里。
观察发现,只有当a的二进制数值都为1111,或者11111,或者111111....这样的情况下,与b进行&运算时,结果才能依次递增, 即结果数据非常松散有规律的递增
而1111,11111,111111这样对应的是十进制的15,31,63,也即是16-1,32-1,64-1,也即是2^4-1, 2^5-1, 2^6-1,都是2的次幂-1
综上原理结论:
1.该算法通过与tab的len长度(n-1)进行&运算,结果result一定是 result<len;即一定在长度内不会越界。
2.该算法只有在len=2的n次幂的情况下,散列能力才正常松散,否则,散列能力会很差,值都会放同一个槽(坑)里跳。
应用结论:
给hashmap指定长度时,一定要指定为2的n次幂。
2.put的时候,key是如何判断是否相同的?
Node<K,V> e; K k;
if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))){
e = p; // hash相等 && key相等 的情况下,用节点e存储原来的已经存在的节点k
logger.info("相同对象");
}
结论:
当且仅当,
h >>> 16

 浙公网安备 33010602011771号
浙公网安备 33010602011771号