UFLDL 教程一总结与答案
UFLDL教程网址:http://ufldl.stanford.edu/wiki/index.php/UFLDL教程
UFLDL教程一练习网址:http://ufldl.stanford.edu/wiki/index.php/Exercise:Sparse_Autoencoder
UFLDL是Unsupervised Feature Learning and Deep Learning的缩写。UFLDL wiki由斯坦福大学计算机系Andrew Ng教授研究组制作,对于深度学习的入门有很大帮助。第一部分是稀疏自编码器,由神经网络、反向传导算法、自编码算法与稀疏性等组成。
1.神经网络
激活函数1:Sigmoid函数: 范围(0,1),导数:f(z)(1-f(z))
范围(0,1),导数:f(z)(1-f(z))
激活函数2:双曲正切函数: .范围(-1,1),导数:1-(f(z))2
.范围(-1,1),导数:1-(f(z))2
神经网络模型:

nl:网络层数,这里值为3,第l层为Ll
(W,b):网络参数,这里为(W1,b1,W2,b2) ,Wijl:第l层j元与第l+1层i元的连接参数,bil:第l+1层第i元的 偏置项,这里W2为R3*3,W1为R1*3
sl:第l层节点数,偏置单元没有输入。
ail:第l层第i单元的输出值。
求解过程:

 即:
即:
2.反向传播
给定样本集: ,利用梯度下降法来求解神经网络,其单样本代价函数:
,利用梯度下降法来求解神经网络,其单样本代价函数: ,对于整体样本:
,对于整体样本:
 第二项是一个规则化项(也叫权重衰减项),其目的是减小权重的幅度,防止过度拟合。
第二项是一个规则化项(也叫权重衰减项),其目的是减小权重的幅度,防止过度拟合。 ![]() 是一个非凸函数,梯度下降法很可能会收敛到局部最优解;但是在实际应用中,梯度下降法通常能得到令人满意的结果。注意初始化时要随机初始化!
是一个非凸函数,梯度下降法很可能会收敛到局部最优解;但是在实际应用中,梯度下降法通常能得到令人满意的结果。注意初始化时要随机初始化!
步骤如下:
1)进行前馈传导计算,利用前向传导公式,得到 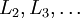 直到输出层
直到输出层 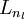 的激活值,即求解a、z等值。
的激活值,即求解a、z等值。
2)对输出层(第 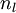 层),计算残差:
层),计算残差:
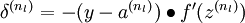 (注意这个负号)
(注意这个负号)
- 3)对于
![\textstyle l = n_l-1, n_l-2, n_l-3, \ldots, 2]() 的各层,计算残差:
的各层,计算残差: -
4)计算单样本偏导数值:
![\begin{align}
\nabla_{W^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} (a^{(l)})^T, \\
\nabla_{b^{(l)}} J(W,b;x,y) &= \delta^{(l+1)}.
\end{align}]()
5)根据反向传播来计算整体样本偏导数值:
![]()
- 以上是反向传播算法的步骤:反向传播计算偏导数的一种有效方法。计算出单样本偏导数后,就可以实现梯度下降法的一次迭代:
-
对于所有
![\textstyle l]() ,令
,令 ![\textstyle \Delta W^{(l)} := 0]() ,
, ![\textstyle \Delta b^{(l)} := 0]() (设置为全零矩阵或全零向量)
(设置为全零矩阵或全零向量)对于
![\textstyle i = 1]() 到
到 ![\textstyle m]() ,
,使用反向传播算法计算
![\textstyle \nabla_{W^{(l)}} J(W,b;x,y)]() 和
和 ![\textstyle \nabla_{b^{(l)}} J(W,b;x,y)]() 。
。计算
![\textstyle \Delta W^{(l)} := \Delta W^{(l)} + \nabla_{W^{(l)}} J(W,b;x,y)]() 。
。计算
![\textstyle \Delta b^{(l)} := \Delta b^{(l)} + \nabla_{b^{(l)}} J(W,b;x,y)]()
更新权重函数:
-
![\begin{align}
W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\
b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b)
\end{align}]() (单样本)
(单样本) ![\begin{align}
W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\
b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right]
\end{align}]() (整体样本,矩阵化)
(整体样本,矩阵化)
-
3.自编码算法与稀疏性
在有监督学习中,训练样本是有类别标签的。现在假设我们只有一个没有带类别标签的训练样本集合 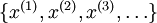 ,其中
,其中 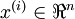 。自编码神经网络是一种无监督学习算法,它使用了反向传播算法,并让目标值等于输入值,比如
。自编码神经网络是一种无监督学习算法,它使用了反向传播算法,并让目标值等于输入值,比如 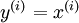 。自编码神经网络尝试学习一个
。自编码神经网络尝试学习一个 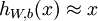 的函数,稀疏性解释:如果当神经元的输出接近于1的时候我们认为它被激活,而输出接近于0的时候认为它被抑制,那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。这里我们假设的神经元的激活函数是sigmoid函数。如果你使用tanh作为激活函数的话,当神经元输出为-1的时候,我们认为神经元是被抑制的。
的函数,稀疏性解释:如果当神经元的输出接近于1的时候我们认为它被激活,而输出接近于0的时候认为它被抑制,那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。这里我们假设的神经元的激活函数是sigmoid函数。如果你使用tanh作为激活函数的话,当神经元输出为-1的时候,我们认为神经元是被抑制的。
回忆上文中反向传播的代价函数J(W,b),在自编码算法的代价函数中只是又增加了一项,即:
-
![\begin{align}
J_{\rm sparse}(W,b) = J(W,b) + \beta \sum_{j=1}^{s_2} {\rm KL}(\rho || \hat\rho_j),
\end{align}]()
-
注意到
![\textstyle a^{(2)}_j]() 表示隐藏神经元
表示隐藏神经元 ![\textstyle j]() 的激活度,但是这一表示方法中并未明确指出哪一个输入
的激活度,但是这一表示方法中并未明确指出哪一个输入 ![\textstyle x]() 带来了这一激活度。所以我们将使用
带来了这一激活度。所以我们将使用 ![\textstyle a^{(2)}_j(x)]() 来表示在给定输入为
来表示在给定输入为 ![\textstyle x]() 情况下,自编码神经网络隐藏神经元
情况下,自编码神经网络隐藏神经元 ![\textstyle j]() 的激活度。
的激活度。 ![\textstyle \rho]() 是稀疏性参数,通常是一个接近于0的较小的值(比如
是稀疏性参数,通常是一个接近于0的较小的值(比如 ![\textstyle \rho = 0.05]() )。换句话说,我们想要让隐藏神经元
)。换句话说,我们想要让隐藏神经元 ![\textstyle j]() 的平均活跃度接近0.05。为了满足这一条件,隐藏神经元的活跃度必须接近于0。
的平均活跃度接近0.05。为了满足这一条件,隐藏神经元的活跃度必须接近于0。 - 计算步骤如下:
1.![\begin{align}\hat\rho_j = \frac{1}{m} \sum_{i=1}^m \left[ a^{(2)}_j(x^{(i)}) \right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/8/7/2/8728009d101b17918c7ef40a6b1d34bb.png) ,表示隐藏神经元
,表示隐藏神经元  的平均活跃度(在训练集上取平均)。
的平均活跃度(在训练集上取平均)。
2.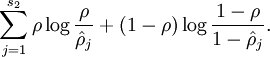 计算惩罚因子,惩罚因子也等于
计算惩罚因子,惩罚因子也等于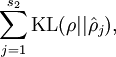 因为
因为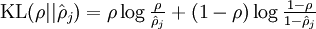 。
。
3.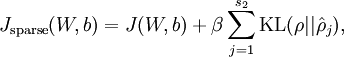 β控制稀疏性惩罚因子的权重。
β控制稀疏性惩罚因子的权重。
至此,代价函数计算完成。但需注意,在自编码算法中计算J(W,b)时,需要改进一步:
将式子 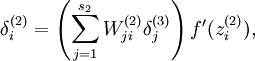 改为
改为 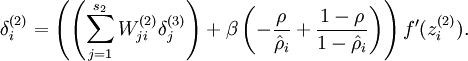
4.代码
1)sampleIMAGES.m
for k=1:numpatches rand_raw=ceil(504*rand); rand_column=ceil(504*rand); rand_image=ceil(10*rand); %将输入的10张512*512的图像IMAGE随机截取为10000张8*8的图像 patches_k=IMAGES(rand_raw:rand_raw+7,rand_column:rand_column+7,rand_image); patches(:,k)=patches_k(:); end
2)sparseAutoencoderCost.m
[m,n]=size(data); %维数:data(64*10000),W1(25*64),W2(64*25),b1(25*1),b2(64*1),a2=f(z2)(25*10000),a3=f(z3)(64*10000)
b1=repmat(b1,1,n); %注意对b的扩展,n=10000
b2=repmat(b2,1,n);
z2=W1*data+b1;
a2=sigmoid(z2);
z3=W2*a2+b2;
a3=sigmoid(z3); %以上计算前向传播
J_W_b=sum(sum((a3-data).^2)/2)/n+(lambda/2)*(sum(sum(W1.^2))+sum(sum(W2.^2))); %计算反向传播整体代价函数 rho=sum(a2,2)/n; KL=sparsityParam.*(log(sparsityParam./rho))+(1-sparsityParam).*log((1-sparsityParam)./(1-rho)); %计算惩罚因子 J_sparse=J_W_b+beta*sum(KL); %计算自编码算法代价函数 cost=J_sparse; delta_rho=beta*(((1-sparsityParam)./(1-rho))-(sparsityParam./rho)); delta3=(a3-data).*a3.*(1-a3); %这里的符号有问题,教程有负号,计算关于W的单样本导数值 delta2=((W2'*delta3)+repmat(delta_rho,1,n)).*a2.*(1-a2); %计算关于b的单样本导数值 W2grad=delta3*a2'/n+lambda*W2; %计算关于W的整体样本导数值 W1grad=delta2*data'/n+lambda*W1; b2grad=sum(delta3,2)/n; b1grad=sum(delta2,2)/n; %计算关于b的整体样本的导数值,权重衰减只作用于W,不作用于b
3)computeNumericalGradient.m
epsilon=1*10^(-4); [a,b]=size(theta); %利用梯度检验进行对比验证 theta_plus=repmat(theta,1,a)+eye(a)*epsilon; theta_minus=repmat(theta,1,a)-eye(a)*epsilon; for i=1:a numgrad(i)=(J(theta_plus(:,i))-J(theta_minus(:,i)))/(2*epsilon); end
5.程序运行结果:
step1:
step3: 梯度检验,检验正确后就跳过此步骤,非常缓慢。。
梯度检验,检验正确后就跳过此步骤,非常缓慢。。
step4 and 5: 400次迭代后结果。
400次迭代后结果。


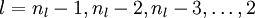 的各层,计算残差:
的各层,计算残差: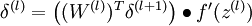
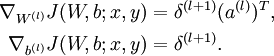

 ,令
,令  ,
,  (设置为全零矩阵或全零向量)
(设置为全零矩阵或全零向量) 到
到 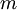 ,
,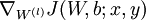 和
和 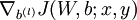 。
。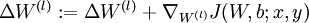 。
。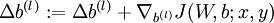
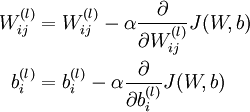 (单样本)
(单样本) ![\begin{align}
W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\
b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right]
\end{align}](http://ufldl.stanford.edu/wiki/images/math/0/f/7/0f7430e97ec4df1bfc56357d1485405f.png) (整体样本,矩阵化)
(整体样本,矩阵化)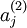 表示隐藏神经元
表示隐藏神经元  带来了这一激活度。所以我们将使用
带来了这一激活度。所以我们将使用 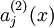 来表示在给定输入为
来表示在给定输入为 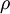 是稀疏性参数,通常是一个接近于0的较小的值(比如
是稀疏性参数,通常是一个接近于0的较小的值(比如 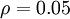 )。换句话说,我们想要让隐藏神经元
)。换句话说,我们想要让隐藏神经元 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号