math

以下这份数学笔记是笔者从 2023 年 7 月开始记录至现在的，.md 源文件达到了 \(152\) KB。目前笔者高二，所学知识尚未完善，部分知识点未齐全，请读者见谅。

以下内容可能加载时间较长，请耐心等待。并且大约消耗 \(1\sim 2\) GB 的内存。

可能存在图片加载不出来的情况或者其他意见建议，请私聊告知我，谢谢！

本笔记可能多次修改，以后可能会多次提交审核，辛苦洛谷管理员们！

方程求解

• 代数基本定理：任何一元 \(n(n\in\N ^{*})\) 次复系数多项式方程 \(f(x)=0\) 至少有一个复数根。

• 一元一次方程

  \(ax+b=0(a\neq 0) \implies x=-\frac{b}{a}\)

• 一元二次方程

  \(ax^2+bx+c=0(a\neq0)\)

  ${\Delta=b^2-4ac} \begin{cases}
  \Delta<0，x=\frac{-b\pm\sqrt{-\Delta}i}{2a} \
  \Delta=0，x=-\frac{b}{2a} \
  \Delta>0，x=\frac{-b\pm\sqrt{\Delta}}{2a},\ 二者相距\ |\frac{\sqrt{\Delta}}{a}| \
  \ \ \ \ \ \ \ \ \ \ \ \ \ \ 顶点坐标\ (-\frac{b}{2a},\ -\frac{\Delta}{4a}),\ 两根相加 -\frac{b}{a},\ 两根相乘 \frac{c}{a} \
  \ \ \ \ \ \ \ \ \ \ \ \ \ \ 其与坐标轴围成的面积\ S=\frac{\Delta^{1.5}}{6a2}
  \end{cases}
  $

• 一元三次方程

  \(ax^3+bx^2+cx+d=0(a\neq0)\)

  1. 盛金公式

     重根判别式 \(\begin{cases} A=b^2-3ac \\ B=bc-9ad \\ C=c^2-3bd \end{cases}\)

     总判别式 \(\Delta=B^2-4AC\)

  • \(A=B=0\)

    \(x_1=x_2=x_3=\frac{-b}{3a}=\frac{-c}{b}=\frac{-3d}{c}\)

  • \(\Delta>0\)

    令 \(Y_{1,2}=Ab+3a(\frac{-B\pm\sqrt{B^2-4AC}}{2}),\ i^2=-1\)

    \(\boxed{x_1=\frac{-b-(\sqrt[3]{Y_1}+\sqrt[3]{Y_2})}{3a}\ \ \ \ \ \ \ \ \ \ \ \ x_{2,3}=\frac{-b+\frac{1}{2}(\sqrt[3]{Y_1}+\sqrt[3]{Y_2})\pm\frac{\sqrt{3}}{2}(\sqrt[3]{Y_1}-\sqrt[3]{Y_2})i}{3a}}\)

  • \(\Delta=0(A\neq 0)\)

    \(\boxed{x_1=\frac{-b}{a}+\frac{B}{A}\ \ \ \ \ \ \ \ \ \ \ \ x_2=x_3=\frac{-B}{2A}}\)

  • \(\Delta<0\)

    \(\boxed{x_1=\frac{-b-2\sqrt{A}\cos\frac{\theta}{3}}{3a}\ \ \ \ \ \ \ \ \ \ \ \ x_{2,3}=\frac{-b+\sqrt{A}(\cos\frac{\theta}{3}\pm\sqrt{3}\sin\frac{\theta}{3})}{3a}}\)

    其中 \(\theta=\arccos \frac{2Ab-3aB}{2\sqrt{A^3}}\ (A>0,-1<T<1)\)

  2. 卡尔达诺公式

     先左右除以 \(a\)，令 \(y=x+\frac{b}{3a}\) 得到一个奇数次的方程 \(y^3+3py+2q=0\)，再令 \(y=u+v\) 得到 \(u^3+v^3+(u+v)(3uv+3p)+2q=0\)

     瞪眼法可以知道 \(u^3+v^3=-2q,uv=-p\) 的一个根，再解出 \(u,v\) 即可。

  \(\begin{cases} x_1+x_2+x_3=-\frac{b}{a} \\ x_1x_2+x_1x_3+x_2x_3=\frac{c}{a} \\ x_1x_2x_3=-\frac{d}{a} \end{cases}\)

• 一元四次方程

  \(ax^4+bx^3+cx^2+dx+e=0(a\neq 0)\)

  \(\begin{cases} x_1+x_2+x_3+x_4=-\frac{b}{a} \\ x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4=\frac{c}{a} \\ x_1x_2x_3+x_1x_2x_4+x_1x_3x_4+x_2x_3x_4=-\frac{d}{a} \\ x_1x_2x_3x_4=\frac{e}{a} \end{cases}\)

• 若将韦达定理推广到一元 \(n\) 次方程 \(a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0=0 (a_n\neq 0)\)，则方程的根可以表示为

  \[x_k = -\frac{1}{n} \displaystyle\sum_{j=1}^{n} \omega^j a_j \]

  其中 \(\omega\) 是 \(n\) 次单位根，即 \(\omega = e^{\frac{2\pi i}{n}}\)

  根的和与系数的关系：\(x_1 + x_2 + \ldots + x_n = -\frac{a_{n-1}}{a_n}\)

  根的积与系数的关系：\(x_1x_2\dots x_n = (-1)^n \frac{a_0}{a_n}\)

• 二元一次方程组

  \(\begin{cases} a_1x+b_1y=c_1 \\ a_2x+b_2y=c_2 \end{cases}\)

  \(\Delta=a_1b_2-b_1a_2 \begin{cases} \Delta=0,\ \text{无解\ 或\ 无数组解} \\ \Delta\neq0,\ \begin{cases} x=\frac{c_1b_2-b_1c_2}{\Delta} \\ y=\frac{a_1c_2-c_1a_2}{\Delta} \end{cases} \end{cases}\)

不等式

以下 \(i=1,2,\dots,n.\)

均值不等式

对于 \(a_i\geq 0\)，有 \(\displaystyle\frac{n}{\sum_{i=1}^{n}\frac{1}{a_i}}\leq\sqrt[n]{\prod_{i=1}^{n}a_i}\leq\frac{\sum_{i=1}^{n}a_i}{n}\leq\sqrt{\frac{\sum_{i=1}^{n}a_i^2}{n}}\)

也就是 调和平均值 \(\leq\) 几何平均值 \(\leq\) 算术平均值 \(\leq\) 平方平均值

加权形式：\(a_i\geq 0,w_i>0\) 且 \(\displaystyle\sum_{i=1}^{n}w_i=1\)，有 \(\displaystyle\prod_{i=1}^{n}a_i^{w_i}\leq\sum_{i=1}^{n}w_ia_i\)

柯西不等式

\[a_i,b_i\in\R\ \ \ \ (\sum_{i=1}^{n}a_ib_i)^2\leq(\sum_{i=1}^{n}a_i^2)(\sum_{i=1}^{n}b_i^2) \]

推论：权方和不等式

\[\frac{(\sum_{i=1}^{n}a_i)^2}{\sum_{i=1}^{n} b_i}\leq\sum_{i=1}^{n}\frac{a_i^2}{b_i} \]

幂平均不等式

\[a_i>0,\alpha>\beta\ \ \ \ (\frac{\sum_{i=1}^{n} a_i^\beta}{n})^{\frac{1}{\beta} }\leq(\frac{\sum_{i=1}^{n}a_i^\alpha}{n})^{\frac{1}{\alpha} } \]

加权形式：\(\displaystyle a_i>0,p_i>0,\alpha>\beta\ \ \ \ \ (\frac{\sum_{i=1}^{n}p_ia_i^{\beta}}{\sum_{i=1}^{n}p_i})^{\frac{1}{\beta}}\leq(\frac{\sum_{i=1}^{n}p_ia_i^{\alpha}}{\sum_{i=1}^{n}p_i})^{\frac{1}{\alpha}}\)

切比雪夫不等式

若 \(a_1\leq a_2\leq\dots\leq a_n,b_1\leq b_2\leq\dots\leq b_n\)，则：

\[(\sum_{i=1}^{n}a_i)(\sum_{i=1}^{n}b_i)\leq n(\sum_{i=1}^{n}a_ib_i) \]

排序不等式

若 \(a_1\leq a_2\leq\dots\leq a_n,b_1\leq b_2\leq\dots\leq b_n\)，则：正序和 \(\geq\) 乱序和 \(\geq\) 反序和

\[a_1b_1+a_2b_2+\dots+a_nb_n\geq x_1b_1+x_2b_2+\dots+x_nb_n\geq a_nb_1+a_{n-1}b_2+\dots+a_1b_n \]

Holder 不等式

\[a_i,b_i\geq 0,p>1,\frac{1}{p}+\frac{1}{q}=1\ \ \ \ \ \ \sum_{i=1}^{n}a_ib_i\leq(\sum_{i=1}^{n}a_i^p)^{\frac{1}{p} }(\sum_{i=1}^{n}b_i^q)^{\frac{1}{q} } \]

琴生不等式

设 \(f(x)\) 为单调区间 \([a,b]\) 的下凸函数，\(x_i\in[a,b]\)

\[\frac{\sum_{i=1}^{n} f(x_i)}{n}\geq f(\frac{\sum_{i=1}^{n} x_i}{n}) \]

例子

• 例 1：已知 \(x>0,y>0,x+y=2\)，求 \(\frac{2}{x}+\frac{3}{y}\) 的最小值。

  \(\frac{2}{x}+\frac{3}{y}=\frac{(\frac{2}{x}+\frac{3}{y})(x+y)}{2}=\frac{5+\frac{2y}{x}+\frac{3x}{y}}{2}\geq\frac{5+2\sqrt{6}}{2}\)

  注意 \(\sin^2\alpha+\cos^2\alpha=1\)

• 例 2：已知 \(a>b>0\)，求 \(a^2+\frac{1}{ab}+\frac{1}{a(a-b)}\) 的最小值。

  \(a^2+\frac{1}{ab}+\frac{1}{a(a-b)}=a^2-ab+ab+\frac{1}{ab}+\frac{1}{a(a-b)}\)

  使用基本不等式化简，取等条件 \(a=\sqrt{2},b=\frac{\sqrt{3}}{2}\)。

• 例 3：已知 \(a>0,b>0,c>0\)，求证 \(\frac{c}{a+b}+\frac{a}{b+c}+\frac{b}{c+a}\geq\frac{3}{2}\)。

  设 \(x=a+b,y=b+c,z=c+a\)，则 \(a=(a+b+c)-(b+c)=\frac{z+x-y}{2}\)。

  同理可得 \(b=\frac{x+y-z}{2},c=\frac{y+z-x}{2}\)，代入原式得左边 \(=\)

  \(\frac{1}{2}(\frac{y}{x}+\frac{x}{y}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y})-\frac{3}{2}\)

  使用基本不等式化简，取等条件 \(x=y=z\)，即 \(a=b=c\)

• 例 4：若实数 \(x,y\) 满足 \(x^2+y^2+xy=1\), 则 \(x+y\) 的最大值是 ？

  使用判别式法，令 \(k=x+y, x=k-y\) 代入得

  \(y^2-ky+k^2-1=0,\ \Delta=k^2-4(k^2-1)\geq 0\)

  得 \(-\frac{2\sqrt{3}}{3}\leq k\leq \frac{2\sqrt{3}}{3}, x+y\leq \frac{2\sqrt{3}}{3}\)。

• 例 5：已知正实数 \(y\) 满足 \(\frac{xy}{y-x}=\frac{1}{5x+4y}\), 则正实数 \(x\) 的最大值是 ？

  由题得 \(4xy^2+(5x^2-1)y+x=0\implies y_1y_2=\frac{1}{4}>0, y_1+y_2=-\frac{5x^2-1}{4x}>0\)。

  \(\therefore \begin{cases} 5x^2-1<0 \\ x>0 \end{cases} 或 \begin{cases} 5x^2-1>0 \\ x<0 \end{cases}\implies 0<x<\frac{\sqrt{5}}{5}\)

  \(\Delta=(5x^2-1)^2-16x^2\geq 0 \implies 5x^2-1\geq 4x\ 或 \ 5x^2-1\leq -4x\)

  解得 \(0< x\leq \frac{1}{5}\)。

• 例 6：\(\Delta ABC\) 中求 \((\frac{S}{a^2+2bc})_{\max}\)。

  所求式中 \(a,b,c\) 等价，故 \(a=b=c\) 时取最值 \(\frac{\sqrt{3}}{12}\)。

函数单调性、奇偶性、对称性与周期性

复合函数单调性——同增异减

\(f(x)\)	\(g(x)\)	\(f(g(x))\)
\(\uparrow\)	\(\uparrow\)	\(\uparrow\)
\(\uparrow\)	\(\downarrow\)	\(\downarrow\)
\(\downarrow\)	\(\uparrow\)	\(\downarrow\)
\(\downarrow\)	\(\downarrow\)	\(\uparrow\)

奇偶性

• 奇函数：对称中心 \((0,0)\)，如 \(y=\frac{k}{x}\ (k\neq 0)\)。

• 偶函数：关于 \(x=0\) 对称，如 \(y=|x|,\ y=x^2\)。

• 一个多项式函数为奇函数，当且仅当它只有奇数次幂，如 \(f(x)=2x^7+5x^5-x^3\)。

• 一个多项式函数为偶函数，当且仅当它只有偶数次幂，如 \(f(x)=x^6-6x^4+x^2+9\)。

• \(y=f(ax+b)+c\) 是奇函数，则 \(f(x)\) 的对称中心 \((b,-c)\)。

• \(y=f(ax+b)+c\) 是偶函数，则 \(f(x)\) 关于 \(x=b\) 对称。

• 反函数：定义域和值域与原函数互换的新函数，如 \(f(x)=\log_ax\) 的反函数为 \(g(x)=a^x\)，反之亦然。

  例：已知函数 \(f(x)=a^{x-1}+3(a>0\ 且 \ a\neq 1)\)，则 \(f(x)\) 的的图像恒过定点 \((1,4) \\ \implies f(x)\) 的反函数的图像恒过定点 \((4,1)\)，即横坐标与纵坐标互换。

  反函数的其他性质：原函数与其反函数关于直线 \(y=x\) 对称。

• \(|奇函数|=偶函数\)。

• 奇偶函数加减法则

\(\text{Type1}\)	\(\text{Operator}\)	\(\text{Type2}\)	\(\text{Result}\)
\(\text{奇}\)	\(\pm\)	\(\text{奇}\)	\(\text{奇}\)
\(\text{偶}\)	\(\pm\)	\(\text{偶}\)	\(\text{偶}\)
\(\text{奇}\)	\(\times\)	\(\text{奇}\)	\(\text{偶}\)
\(\text{偶}\)	\(\times\)	\(\text{偶}\)	\(\text{偶}\)
\(\text{奇}\)	\(\times\)	\(\text{偶}\)	\(\text{奇}\)

• 复合函数奇偶性（有偶则偶，同奇则奇）

\(f(x)\)	\(g(x)\)	\(f(g(x))\)
奇	奇	奇
奇	偶	偶
偶	奇	偶
偶	偶	偶

对称性

必记二级结论

• \(f(a+x)=f(b-x) \implies 关于 \ x=\frac{a+b}{2}\ 对称\)。

• \(f(a+x)+f(b-x)=c \implies 对称中心 \ (\frac{a+b}{2},\frac{c}{2})\)。

以下记 \(T\) 为函数的周期, 记 \(C\in\R\) 为某个常数。

• \(f(x+a)=f(x+b) \implies T=|b-a|\)

• \(f(x)+f(x+a)=C \implies T=2a\)

• \(f(x)\times f(x+a)=C \implies T=2a\)

• \(f(x+2a)=f(x+a)-f(x) \implies T=6a\)

• \(f(x)\ 关于\ x=a,\ x=b\ 对称 \implies T=|2(b-a)|\)

• \(f(x)\ 的两个对称中心\ (a,0),\ (b,0)\ \implies T=|2(b-a)|\)

• \(f(x)\ 关于\ x=a\ 对称且有个对称中心\ (b,0) \implies T=|4(b-a)|\)

拓展二级结论

• 三次及以下的多项式函数具有一般对称性，四次及以上的多项式函数不具有一般对称性。

  最高幂次为奇数的多项式函数只可能具有中心对称性，最高幂次为偶数的多项式函数只可能具有轴对称性。

  如果一个多项式函数 \(f(x)=a_n x^n + a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) 具有中心对称性，那么它的对称中心 \((-\frac{a_{n-1}}{na_n},f(-\frac{a_{n-1}}{na_n}))\)。

  如果一个多项式函数 \(f(x)=a_n x^n + a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) 具有轴对称性，那么它的对称轴 \(x=-\frac{a_{n-1}}{na_n}\)。

• \(f(x)=\frac{ax+b}{cx+d}\) 的对称中心 \((-\frac{d}{c},\frac{a}{c})\)。

  注意到该函数的定义域为 \(\set{x|x\neq - \frac{d}{c}}\)，值域是 \(\set{x|x\neq\frac{a}{c}}\)。

  例：\(f(x)=\frac{x}{x+1}+\frac{x+1}{x+2}+\frac{x+2}{x+3}\) 的对称中心 ？

  首先我们知道，这三个式子的对称中心分别是 \((-1,1)\)，\((-2,1)\)，\((-3,1)\)。

  如果这个函数有对称中心，其横坐标就在 \(-1,-2,-3\) 中间即 \(-2\)。

  因为函数是三个式子相加，所以纵坐标就是三个纵坐标相加即 \(3\)。

  所以函数的对称中心 \((-2,3)\)。

• \(f(x)=\frac{t}{a^{x-k}+1}\) 的对称中心 \((k,f(k))\) 即 \((k,\frac{t}{2})\)。

• \(f(x)=ax^3+bx^2+cx+d\) 的对称中心 \((-\frac{b}{3a},f(-\frac{b}{3a}))\)。

• \(f(|ax+b|)\) 关于 \(x=-\frac{b}{a}\) 对称 且 \(f(|ax+b|)\) 在 \(x>-\frac{b}{a}\) 时与 \(f(t)\) 的单调性相同。

• 任何一个函数 \(f(x)\) 都可以拆分为一个奇函数 \(F(x)=\frac{f(x)-f(-x)}{2}\) 与一个偶函数 \(G(x)=\frac{f(x)+f(-x)}{2}\) 之和。

• \(f(x+a)=\frac{mf(x)+b}{cf(x)-m}(a,b,c\in\R,c\neq 0,m^2+bc\neq 0) \implies T=2a\)

• \(f(x+a)=\frac{1+f(x)}{1-f(x)} \implies T=4a\)

幂、对数的基本计算

• \(x^a\ (a\ 为有理数)=\begin{cases} a\in\Z^+,\ 直接计算 \\ a=0,\ x^a=0 \\ a\in\Z^-,\ x^a=\frac{1}{x^{-a}} \\ \text{Otherwise} ,\ 令 \ a=\frac{b}{c}, \ x^a=\sqrt[c]{x^b} \\ \end{cases}\)

• \(\log_ab+\log_ac=\log_a bc\)

• \(\log_ab-\log_ac=\log_a\frac{b}{c}\)

• \(\log_ab=\frac{\log_ca}{\log_cb}\)

• \(\frac{b}{c}\log_aN=\log_{a^c}N^b\)

• \(M^{\log_aN}=N^{\log_aM}\)

• \(a^{\lg b}=b^{\lg a}\)

例子

• 例 1：已知正实数 \(x,y,z\) 满足 \(3^x=5^y=15^z\)，则 （ BCD ）

  A. $x+y=z\ \ \ \ \ \ \text{} $ B. \(xz+yz=xy\ \ \ \ \ \ \text{}\) C. $\frac{x}{3}>\frac{y}{5}>\frac{z}{15}\ \ \ \ \ \ \text{} $ D. \(xy>4z^2\)

  令 \(3^x=5^y=15^z=k\)，则 \(x=\log_{3}k\)，\(y=\log_{5}k\)，\(z=\log_{15}k\)。

  令 \(k=100\) 易证 A 选项不成立。

  显然有 \(\frac{1}{x}=\log_{k}3\)，\(\frac{1}{y}=\log_{k}5\)，\(\frac{1}{z}=\log_{k}15\)。

  即 \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\)，两边同乘 \(xyz\) 可证得 B 选项成立。

  C 选项题意转化得 \(\frac{3}{x}<\frac{5}{x}<\frac{15}{x}\)，易证其成立。

  D 选项即证明 \(xy-4z^2=\frac{(\lg{k})^2}{\lg 3\lg 5}-\frac{4(\lg{k})^2}{(\lg{15})^2}>0 \implies (\lg{15})^2-4\lg{3}\lg{5}=(\lg 3+\lg 5)^2-4\lg{3}\lg{5}=(\lg 3-\lg 5)^2>0\)。

• 例2：设 \(a=\log_{3}2,b=\log_{5}3,c=\log_{8}5\)，比较大小：\(a<b<c\)。

  \(\because (a+b)^2\geq 4ab\ \ \ \ \ \ \text{}\) \(\therefore ab\leq\frac{(a+b)^2}{4}\)

  \(\frac{b}{c}=\log_{5}3\times\log_{5}8\leq\frac{(\log_{5}3+\log_{5}8)^2}{4}<1\implies b<c\)

  \(\log_{3}2=\log_{3}\sqrt[3]{8}<\log_{3}\sqrt[3]{9}=\frac{2}{3},\log_{5}3=\log_{5}\sqrt[3]{27}>\log_{5}\sqrt[3]{25}=\frac{2}{3}\implies a<b\)

复数

• \(z=a+b\text{i}\) \(\ \ \ \ \ \text{}\) 模或绝对值 \(|z|=|a+b\text{i}|=\sqrt{a^2+b^2}\)

  共轭复数 \(\={z}=a-b\text{i}\) \(\ \ \ \ \ \text{}\) 几何意义：复平面上点 \((a,b)\)

  注意实部为 \(a\)，虚部为 \(b\) （不带 \(\text{i}\)）\(\ \ \ \ \ \text{}\)。 注意当 \(a=0,b\neq 0\) 时为纯虚数，\(0\) 不是纯虚数。

  所有虚数均不能直接比较大小，如 \(\xcancel{2+\text{i}>1+\text{i}}\)，当且仅当 \(b=0\) 时可以比较。

• \(z_1=a+b\text{i},\ z_2=c+d\text{i}\) \(\ \ \ \ \ \text{}\implies\) \(z_1\pm z_2=(a\pm c)+(b\pm d)\text{i}\)

  \(\implies z_1 z_2=ac-bd+(bc+ad)\text{i}\) \(\ \ \ \ \ \text{}\) \(\frac{z_1}{z_2}=\frac{ac+bd+(bc-ad)\text{i}}{c^2+d^2}\)

  利用三角形三边关系：\(|z_1|-|z_2|\leq|z_1+z_2|\leq|z_1|+|z_2|\)。
  此公式适用于实数、复数、向量，当 \(a,b\) 为向量时，利用 \(|\mathbf{a}\cdot\mathbf{b}|\leq|\mathbf{a}||\mathbf{b}|\) 可证明。

• \((a\pm b\text{i})^2=a^2-b^2\pm 2ab\text{i},(a+b\text{i})(a-b\text{i})=a^2+b^2,(1\pm\text{i})^2=\pm 2\text{i}\)

  \((-\frac{1}{2}\pm\frac{\sqrt{3}\text{i}}{2})^3=1\)

  \(\frac{1}{\text{i}}=-\text{i},\frac{1-\text{i}}{1+\text{i}}=-\text{i},\frac{1+\text{i}}{1-\text{i}}=\text{i}\)

  \(n\in\Z,i^{4n}=1,i^{4n+1}=i,i^{4n+2}=-1,i^{4n+3}=-i\)

复数的三角表示

\[a+b\text{i}=r(\cos\theta+\text{i}\sin\theta) \]

其中 \(r=\sqrt{a^2+b^2},\tan\theta=\frac{b}{a}(a\neq 0)\implies a=r\cos\theta,b=r\sin\theta\)。

规定在 \(0\leq\theta<2\pi\) 时 \(\theta\) 为辐角的主值，记为 \(\arg z\)，且满足 \(0\leq\arg z<2\pi\)。

• 设 \(z_1=a+b\text{i}=r_1(\cos\theta _1+\text{i}\sin\theta _1),z_2=c+d\text{i}=r_2(\cos\theta _2+\text{i}\sin\theta _2)\)

  \(z_1z_2=r_1r_2[\cos(\theta _1+\theta _2)+\text{i}\sin(\theta _1+\theta _2)]\)

  \(\frac{z_1}{z_2}=\frac{r_1}{r_2}[\cos(\theta _1-\theta _2)+\text{i}\sin(\theta _1-\theta _2)](z_2\neq 0)\)

  \(z_1z_2\dots z_n=r_1r_2\dots r_n[\cos(\theta _1+\theta _2+\dots +\theta _n)+\text{i}\sin(\theta _1+\theta _2+\dots +\theta _n)]\)

• 棣莫弗定理：对于 \(z=r(\cos\theta+\text{i}\sin\theta), z^n=r^n(\cos n\theta+\text{i}\sin n\theta),n\in\N ^{*}\)。

复数与圆

• \(|z|=r\implies z\) 在复平面内对应点的集合是以原点为圆心，\(r\) 为半径的圆。

  \(|z-z_1|=r\implies z\) 在复平面内对应点的集合是以 \(z_1\) 在复平面内的对应点为圆心，\(r\) 为半径的圆。

  \(|z-z_1|=|z-z_2|\implies z\) 在复平面内对应点的集合是 \(Z_1,Z_2\) 为端点的线段的中垂线。

• 设复数 \(z_1,z_2,z_1+z_2\) 在复平面内对应点为 \(A,B,C\)，结合平面向量的基本运算。

  \(|z_1+z_2|=|z_1-z_2|\implies\) 四边形 \(\text{OACB}\) 为矩形。

  \(|z_1|=|z_2|\implies\) 四边形 \(\text{OACB}\) 为菱形。

  \(|z_1|=|z_2|\) 且 \(|z_1+z_2|=|z_1-z_2|\implies\) 四边形 \(\text{OACB}\) 为正方形。

• 综合题：已知复数 \(z_1,z_2\) 满足 \(|z_1|=|z_2|=1\)，若 \(|z_1-z_2|=|z_1-1|=|z_2-z|\)，则 \(|z|\) 的最大值是 ？

  \(|z|=|(z_2-z)-z_2|\leq|z_2-z|+|z_2|=|z_1-1|+1\leq|z_1|+1+1=3\)，此时 \(z_1=-1,z_2=1,z=3\)

三角恒等变换

诱导公式

\(\begin{aligned}\sin(\alpha + 2k\pi)&=\sin\alpha,k \in \Z \\ \cos(\alpha + 2k\pi)&=\cos\alpha,k \in \Z \\ \tan(\alpha + 2k\pi)&=\tan\alpha,k \in \Z\end{aligned}\)	\(\begin{aligned}\sin(\pi+\alpha)&=-\sin\alpha \\ \cos(\pi+\alpha)&=-\cos\alpha \\ \tan(\pi+\alpha)&=\tan\alpha\end{aligned}\)	\(\begin{aligned}\sin(-\alpha)&=-\sin\alpha \\ \cos(-\alpha)&=\cos\alpha \\ \tan(-\alpha)&=-\tan\alpha\end{aligned}\)
\(\begin{aligned}\sin(\pi-\alpha)&=\sin\alpha \\ \cos(\pi-\alpha)&=-\cos\alpha \\ \tan(\pi-\alpha)&=-\tan\alpha\end{aligned}\)	\(\begin{aligned}\sin(\frac{\pi}{2}-\alpha)&=\cos\alpha \\ \cos(\frac{\pi}{2}-\alpha)&=\sin\alpha \\ \sin(\frac{\pi}{2}+\alpha)&=\cos\alpha \\ \cos(\frac{\pi}{2}+\alpha)&=-\sin\alpha \\ \tan(\frac{\pi}{2}-\alpha)&=\cot \alpha \\ \cot(\frac{\pi}{2}-\alpha)&=\tan \alpha \\ \sec(\frac{\pi}{2}-\alpha)&=\csc\alpha \\ \csc(\frac{\pi}{2}-\alpha)&=\sec\alpha\end{aligned}\)	\(\begin{aligned}\sin(\frac{3\pi}{2}+\alpha)&=-\cos\alpha \\ \cos(\frac{3\pi}{2}+\alpha)&=\sin\alpha \\ \sin(\frac{3\pi}{2}-\alpha)&=-\cos\alpha \\ \cos(\frac{3\pi}{2}-\alpha)&=-\sin\alpha\end{aligned}\)

• 毕达哥拉斯定理：\(\sin^2\alpha+\cos^2\alpha=1\)，两边同除 \(\sin^2x\) 或 \(\cos^2x\) 可得 \(1+\tan^2x=\sec^2x,1+\cot^2x=\csc^2x\)。

• \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha},\cot x=\frac{1}{\tan x},\sec x=\frac{1}{\cos x},\csc x=\frac{1}{\sin x}\)

• 奇函数：\(\sin,\tan,\cot,\csc\ \ \ \ \text{}\) 偶函数：\(\cos,\sec\)

简单的三角恒等变换

\(\cos(\alpha-\beta)=\cos\alpha \cos\beta+\sin\alpha \sin\beta \\ \cos(\alpha+\beta)=\cos\alpha \cos\beta-\sin\alpha \sin\beta\)	\(\cos 2\alpha=\cos^2\alpha-\sin^2\alpha\\=1-2\sin^2\alpha=2\cos^2\alpha-1\\=(\cos\alpha+\sin\alpha)(\cos\alpha-\sin\alpha)\)	\(\cos\frac a 2=\pm \sqrt{\frac{1+\cos\alpha}{2}}\)
\(\sin(\alpha-\beta)=\sin\alpha \cos\beta-\cos\alpha \sin\beta \\ \sin(\alpha+\beta)=\sin\alpha \cos\beta+\cos\alpha \sin\beta\)	\(\sin 2\alpha=2\sin\alpha \cos\alpha\)	\(\sin\frac a 2=\pm \sqrt{\frac{1-\cos\alpha}{2}}\)
\(\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha \tan\beta} \\ \tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha \tan\beta}\)	\(\tan 2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}\)	\(\tan\frac a 2=\pm \sqrt{\frac{1-\cos\alpha}{1+\cos\alpha}}\\ =\frac{\sin\alpha}{1+\cos\alpha}=\frac{1-\cos\alpha}{\sin\alpha}\)
\(\begin{aligned}\sin 3\alpha&=3\sin\alpha-4\sin^3\alpha \\ \cos 3\alpha&=4\cos^3\alpha-3\cos\alpha \\ \tan 3\alpha&=\frac{3\tan\alpha-\tan^3\alpha}{1-3\tan^2\alpha}\end{aligned}\)	\(\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2} \\ \sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2} \\ \cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2} \\ \cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}\)	\(\sin\alpha=\frac{2\tan\frac{\alpha}{2}}{1+\tan^2\frac{a}{2}}=\frac{\sin2\alpha}{2\cos\alpha} \\ \cos\alpha=\frac{1-\tan^2\frac{a}{2}}{1+\tan^2\frac{a}{2}}=\frac{\sin2\alpha}{2\sin\alpha} \\ \tan\alpha=\frac{2\tan\frac{\alpha}{2}}{1-\tan^2\frac{a}{2}}\\=\frac{(1-\tan^2\alpha)\tan2\alpha}{2}\)

• \(A\sin\alpha+B\cos\alpha=\sqrt{A^2+B^2}\sin(\alpha+\varphi)\) , 其中 \(\tan\varphi={B\over A}\)，\(\tan\varphi<0\) 时，需检验 \(\varphi\) 位于第二象限还是第四象限。

• \(\sin(\alpha+\beta)\sin(\alpha-\beta)=\sin^2\alpha-\sin^2\beta\)

• \(\cos(\alpha+\beta)\cos(\alpha-\beta)=\cos^2\alpha-\sin^2\beta\)

• \(1+\cos\alpha=2\cos^2\frac{a}{2}\)，\(1-\cos\alpha=2\sin^2\frac{a}{2}\)

• \(\tan^2\alpha\sin^2\alpha=\tan^2\alpha-\sin^2\alpha\)

• 对于任意非直角三角形中，总有 \(\tan A+\tan B+\tan C=\tan A\tan B\tan C\)

  经典值：\(\tan A=1,\ \tan B=2,\ \tan C=3\), 此时 \(A=45\degree,\ B=63.43\degree,\ C=71.57\degree\)

• 其他三角形恒等式（ \(\Delta ABC\) 中 ）：\(\begin{cases} \sin A+\sin B+\sin C=4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2} \\ \cos A+\cos B+\cos C=1+4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2} \\ \cot A+\cot B+\cot C=4\cot\frac{A}{2}\cot\frac{B}{2}\cot\frac{C}{2} \\ \sin^2 A+\sin^2 B+\sin^2 C=2+2\cos A\cos B\cos C \\ \cos^2A+ \cos^2B+\cos^2C=1-2\cos A\cos B\cos C \\ \sin 2A+\sin 2B+\sin 2C=4\sin A\sin B\sin C \\ \cos 2A+\cos 2B+\cos 2C=-1-4\cos A\cos B\cos C\\ \tan\frac{A}{2}\tan\frac{B}{2}+\tan\frac{B}{2}\tan\frac{C}{2}+\tan\frac{A}{2}\tan\frac{C}{2}=1 \end{cases}\)

• 若已知 \(\tan \alpha=k,\) 则有 \(\frac{a\sin\alpha+b\cos\alpha}{m\sin\alpha+n\cos\alpha}=\frac{ak+b}{mk+n}\)。

• \(\frac{1-\tan\alpha}{1-\tan^2\alpha}=\frac{1}{2}\tan 2\alpha\)，\(\frac{1-\tan\alpha}{1+\tan^2\alpha}=\frac{1}{2}\sin 2\alpha\)

• 对于 \(x\in (0,\frac{\pi}{2}),\ \sin x<x<\tan x\)。

三角函数的平移

• \(y=A\sin(\omega x+\varphi)+h\ 或\ y=A\cos(\omega x+\varphi)+h \implies T=\frac{2\pi}{|\omega|}\)

  三角函数的应用：振幅 \(A\) 周期 \(T=\frac{2\pi}{\omega}\) 频率 \(f=\frac{1}{T}=\frac{\omega}{2\pi}\) 相位 \(\omega x+\varphi\) 初相 \(\varphi\)

• \(y=A\tan(\omega x+\varphi)+h\implies T=\frac{\pi}{|\omega|}\)

• 三角函数里图像的平移都是针对单个 \(x\) 进行 左加右减。

  例：\(y=3\sin(2x+\frac{\pi}{3})+1\) 向左平移 \(\frac{\pi}{4}\) 个单位长度，再将图像上所有点的横坐标缩短为原来的 \(\frac{1}{2}\)：

  \(y=3\sin(2x+\frac{\pi}{3})+1 \implies y=3\sin[2(x+\frac{\pi}{6})]+1\)

  第一步转移变成 \(y=3\sin[2(x+\frac{\pi}{6}+\frac{\pi}{4})]+1 \implies y=3\sin(2x+\frac{5\pi}{6})+1\)

  第二步转移变成 \(y=3\sin(4x+\frac{5\pi}{6})+1\)

三角不等式

若 \(\alpha,\beta,\gamma\) 为同一个三角形的内角，则有下列不等式：（ 取等条件均为 \(\alpha=\beta=\gamma = \frac{\pi}{3}\) ）

\(\begin{aligned}\sin\alpha+\sin\beta+\sin\gamma&\leq\frac{3\sqrt{3}}{2} \\ \cos\alpha+\cos\beta+\cos\gamma&\leq\frac{3}{2} \\ \sin\alpha\sin\beta\sin\gamma&\leq\frac{3\sqrt{3}}{8} \\ \cos\alpha\cos\beta\cos\gamma&\leq\frac{1}{8}\end{aligned}\)	\(\begin{aligned}\sin^2\alpha+\sin^2\beta+\sin^2\gamma&\leq\frac{9}{4} \\ \cos^2\alpha+\cos^2\beta+\cos^2\gamma&\geq\frac{3}{4} \\ \tan\alpha+\tan\beta+\tan\gamma&\geq 3\sqrt{3}\ (\ 锐角三角形\ ) \\ \cot\alpha+\cot\beta+\cot\gamma&\geq\sqrt{3}\end{aligned}\)
\(\begin{aligned}\sin\frac{\alpha}{2}+\sin\frac{\beta}{2}+\sin\frac{\gamma}{2}&\leq\frac{3}{2} \\ \cos\frac{\alpha}{2}+\cos\frac{\beta}{2}+\cos\frac{\gamma}{2}&\leq\frac{3\sqrt{3}}{2} \\ \sin\frac{\alpha}{2}\sin\frac{\beta}{2}\sin\frac{\gamma}{2}&\leq\frac{1}{8} \\ \cos\frac{\alpha}{2}\cos\frac{\beta}{2}\cos\frac{\gamma}{2}&\leq\frac{3\sqrt{3}}{8}\end{aligned}\)	\(\begin{aligned}\sin^2\frac{\alpha}{2}+\sin^2\frac{\beta}{2}+\sin^2\frac{\gamma}{2}&\geq\frac{3}{4} \\ \cos^2\frac{\alpha}{2}+\cos^2\frac{\beta}{2}+\cos^2\frac{\gamma}{2}&\leq\frac{9}{4} \\ \tan\frac{\alpha}{2}+\tan\frac{\beta}{2}+\tan\frac{\gamma}{2}&\geq\sqrt{3} \\ \cot\frac{\alpha}{2}+\cot\frac{\beta}{2}+\cot\frac{\gamma}{2}&\geq 3\sqrt{3}\end{aligned}\)

平面向量

定义及基本运算

• 我们把既有大小又有方向的量称为向量，把只有大小没有方向的量称为数量。向量用有向线段 \(\overrightarrow{AB}\) 表示（ 但向量 \(\neq\) 有向线段 ），它的长度/模记作 \(|\overrightarrow{AB}|\)。
  长度等于 \(1\) 个单位长度的向量，称为单位向量，一般用 \(\mathbf{e}\) 表示。长度等于 \(0\) 个单位长度的向量，称为零向量，用 \(\mathbf{0}\) 表示，它的方向是任意的。坐标轴不能说是向量（ 没有长度 ）。

• 平行向量 / 共线向量：方向 相同 或 相反 的非零向量叫做平行向量。零向量与任何向量平行。所以 \(\mathbf{a}//\mathbf{b},\mathbf{b}//\mathbf{c}\ \xcancel{\implies}\ \mathbf{a}//\mathbf{c}\)。

  向量 \(\mathbf{a}(\mathbf{a}\neq\mathbf{0})\) 与 \(\mathbf{b}\) 共线 \(\Longleftrightarrow\) 存在唯一一个实数 \(\lambda\) 使 \(\mathbf{b}=\lambda\mathbf{a}\)。

• 相等向量：长度相等 且 方向相同的两个向量。相反向量：长度相等 且 方向相反的两个向量。

• 投影向量：设 \(\overrightarrow{AB}=\mathbf{a},\overrightarrow{CD}=\mathbf{b}\)，过 \(\overrightarrow{AB}\) 的起点 \(A\) 和终点 \(B\)，分别作 \(\overrightarrow{CD}\) 所在直线的垂线，垂足分别为 \(A_1,B_1\) 并得到 \(\overrightarrow{A_1B_1}\)，称上述变换为向量 \(\mathbf{a}\) 向向量 \(\mathbf{b}\) 投影，\(\overrightarrow{A_1B_1}\) 叫做向量 \(\mathbf{a}\) 在向量 \(\mathbf{b}\) 上的投影向量。

• 两个向量之间的夹角可用 \(\theta=\langle\mathbf{a},\mathbf{b}\rangle\) 表示，注意两个向量此时必须共顶点。

\(\theta\)	\(0\)	\(\pi\)	\(\frac{\pi}{2}\)
\(\mathbf{a}\) 与 \(\mathbf{b}\) 的关系	\(\mathbf{a}\) 与 \(\mathbf{b}\) 同向	\(\mathbf{a}\) 与 \(\mathbf{b}\) 反向	\(\mathbf{a}\) 与 \(\mathbf{b}\) 垂直 记作 \(\mathbf{a}\perp\mathbf{b}\)

运算符	运算法则	性质
\(+\)	平行四边形法则
\(-\)	转化为相反向量后用平行四边形法则	\(-\overrightarrow{AB}=\overrightarrow{BA}\)
数乘	实数 \(\lambda\) 与向量 \(\mathbf{a}\) 的积仍是向量，记作 \(\lambda\mathbf{a}\)	\(| \lambda\mathbf{a} | = | \lambda | | \mathbf{a} |\)，满足交换律，结合律
点乘 \(\cdot \\\) ( 内积/数量积 )	\(\mathbf{a}\cdot\mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos\theta,\theta=\langle \mathbf{a},\mathbf{b} \rangle\)	\(\mathbf{a}\perp\mathbf{b}\Longleftrightarrow\mathbf{a}\cdot\mathbf{b}=0,|\mathbf{a}\cdot\mathbf{b}|\leq|\mathbf{a}||\mathbf{b}|\)，满足交换律，不满足结合律，不能约分\(\\\) 即 \((\mathbf{a}\cdot\mathbf{b})\mathbf{c}\neq\mathbf{a}(\mathbf{b}\cdot\mathbf{c})\)，但 \((\mathbf{a}+\mathbf{b})\cdot\mathbf{c}=\mathbf{a}\cdot\mathbf{c}+\mathbf{b}\cdot\mathbf{c}\)
叉乘 \(\times \\\) ( 外积/向量积 )	\(\mathbf{a}\times\mathbf{b}=\mathbf{c}\)，其中 \(\\ |\mathbf{c}|=|\mathbf{a}||\mathbf{b}|\sin\theta,\theta=\langle \mathbf{a},\mathbf{b} \rangle\)

向量的 \(+,-,\) 数乘运算统称为向量的线性运算，向量线性运算的结果仍为向量。点乘运算叫做 \(\mathbf{a}\) 与 \(\mathbf{b}\) 的数量积/内积，结果为数量。

定理及二级结论

• 平面向量基本定理：若 \(\mathbf{e_1,e_2}\) 是同一平面内的两个不共线向量，则对于这一平面内的任意向量 \(\mathbf{a}\)，有且只有一对实数 \(\lambda _1,\lambda _2\)，使得 \(\mathbf{a}=\lambda _1\mathbf{e_1}+\lambda _2\mathbf{e_2}\)。

  若 \(\mathbf{e_1,e_2}\) 不共线，我们把 \(\set{\mathbf{e_1,e_2}}\) 叫做这一平面内所有向量的一个 基底；任一向量都可以由同一个基底唯一表示。

• 定比分点公式：已知点 \(D\) 为线段 \(BC\) 靠近点 \(B\) 的第 \(k\) 个 \(n\) 等分点 \(\implies \overrightarrow{AD}=\frac{k}{n}\overrightarrow{AC}+\frac{n-k}{n}\overrightarrow{AB}\)，其中 \(A\) 为平面内任取的一点。

  已知 \(A(x_1,y_1),B(x_2,y_2),P(x,y)\)，若 \(\overrightarrow{AP}=\lambda\overrightarrow{PB}\)，则 \(x=\frac{x_1+\lambda x_2}{1+\lambda},y=\frac{y_1+\lambda y_2}{1+\lambda}\)。

• \(||\mathbf{a}|-|\mathbf{b}||\leq|\mathbf{a}\pm\mathbf{b}|\leq|\mathbf{a}|+|\mathbf{b}|\)，应用不等式时，必须验证 等号成立的条件。

• \(|\mathbf{a}|=|\mathbf{b}|=|\mathbf{a}-\mathbf{b}|\implies\) 正三角形 \(\ \ \ \ \ \ \ \ \text{}\) \(|\mathbf{a}+\mathbf{b}|=|\mathbf{a}-\mathbf{b}|\implies\) 矩形

  \(|\mathbf{a}|=|\mathbf{b}|\implies\) 菱形 \(\ \ \ \ \ \ \ \ \text{}\) \(|\mathbf{a}+\mathbf{b}|=|\mathbf{a}-\mathbf{b}|\) 且 \(|\mathbf{a}|=|\mathbf{b}|\implies\) 正方形

• 正弦定理：\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{a+b+c}{\sin A+\sin B+\sin C}=2R=D\)，其中 \(R\) 为三角形外接圆半径。

  变形：要证 \((a+b)(\sin A-\sin B)=(c-b)\sin C\)，可转化为 \((a+b)(a-b)=(c-b)c\implies b^2+c^2-a^2=bc\implies\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{1}{2}\)。

  注意 \(\sin C=\sin(\pi-(A+B))=\sin(A+B)=\sin A\cos B+\cos A\sin B\)。

• 余弦定理：\(\begin{cases} a^2=b^2+c^2-2bc\cos A \\ b^2=a^2+c^2-2ac\cos B \\ c^2=a^2+b^2-2ab\cos C \end{cases}\implies\begin{cases} \cos A=\frac{b^2+c^2-a^2}{2bc} \\ \cos B=\frac{c^2+a^2-b^2}{2ac} \\ \cos C=\frac{a^2+b^2-c^2}{2ab}\end{cases}\)

• 正切定理：\(\displaystyle\frac{a+b}{a-b}=\frac{\tan\frac{a+b}{2}}{\tan\frac{a-b}{2}}\)

• 任意三角形射影定理（ 将 \(\cos\) 展开即可证明 ）：\(\begin{cases} a=b\cos C+c\cos B \\ b=a\cos C+c\cos A \\ c=a\cos B+b\cos A \end{cases}\)

• 极化恒等式：\(\mathbf{a}\cdot\mathbf{b}=(\frac{\mathbf{a}+\mathbf{b}}{2})^2-(\frac{\mathbf{a}-\mathbf{b}}{2})^2\)

  对于平行四边形 \(ABCD\)，满足 \(AC^2+BD^2=2(AB^2+AD^2),\overrightarrow{AB}\cdot\overrightarrow{AD}=\frac{1}{4}(\overrightarrow{AC}^2-\overrightarrow{BD}^2)\)。

  对于三角形 \(ABC\)，\(M\) 为 \(BC\) 中点，\(\overrightarrow{AB}\cdot\overrightarrow{AC}=\overrightarrow{AM}^2-\frac{1}{4}\overrightarrow{BC}^2=\overrightarrow{AM}^2-\overrightarrow{BM}^2\)。

• 对任意四边形 \(ABCD\)，若两对角线相垂直，则 \(S=\frac{1}{2}|\overrightarrow{AC}||\overrightarrow{BD}|\)。

• 中线长定理：对于三角形 \(ABC\)，\(AD\) 为 \(BC\) 边上的中线，则有 \(AB^2+AC^2=2(AD^2+BD^2)\\ \overrightarrow{AB}\cdot\overrightarrow{AC}=|\overrightarrow{AD}|^2-|\overrightarrow{BD}|^2\)。

• 张角定理：\(\Delta ABC,D\) 在 \(BC\) 上，令 \(\angle BAD=\alpha,\angle CAD=\beta\)，则有 \(\frac{\sin\alpha}{AC}+\frac{\sin\beta}{AB}=\frac{\sin(\alpha+\beta)}{AD}\)。

• 奔驰定理：点 \(O\) 是 \(\Delta ABC\) 所在平面内不与 \(A,B,C\) 重合的一点，若 \(x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}=\mathbf{0},xyz\neq 0\)，则 \(S_{\Delta OBC}\overrightarrow{OA}+S_{\Delta OAC}\overrightarrow{OB}+S_{\Delta OAB}\overrightarrow{OC}=\mathbf{0}\)，且 \(S_{\Delta OBC}:S_{\Delta OAC}:S_{\Delta OAB}=x:y:z\)。

  证明：\(x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}=\mathbf{0} \implies \frac{x}{y}\overrightarrow{OA}+\overrightarrow{OB}+\frac{z}{y}\overrightarrow{OC}=\mathbf{0}\)。

  将 \(OA\) 延长到 \(OE\) 满足 \(OE=\frac{x}{y}OA\)，\(OC\) 延长到 \(OF\) 满足 \(OF=\frac{z}{y}OC\)，变为 \(\overrightarrow{OE}+\overrightarrow{OB}+\overrightarrow{OF}=\mathbf{0}\)。

  \(O\) 为 \(\Delta EBF\) 重心，于是有 \(S_{\Delta OBE}=S_{\Delta OEF}=S_{\Delta OBF}\)，\(\frac{S_{\Delta AOC}}{S_{\Delta EOF}}=\frac{\frac{1}{2}OA\cdot OC\cdot \sin\angle AOC}{\frac{1}{2}OE\cdot OF\cdot\sin\angle EOF}=\frac{y}{x}\cdot\frac{y}{z}=\frac{y^2}{xz}\)。

  同理根据相似 \(S_{\Delta AOC}:S_{\Delta AOB}:S_{\Delta BOC}=\frac{y^2}{xz}:\frac{yz}{xz}:\frac{xy}{xz}=y:z:x\)。

例题：\(\Delta ABC\) 中，\(D\) 为 \(BC\) 中点，\(BE=2EA\)，\(AD\) 与 \(CE\) 交于 \(O\)，\(\overrightarrow{AB}\cdot\overrightarrow{AC}=6\overrightarrow{AO}\cdot\overrightarrow{EC},\frac{AB}{AC}=(\ \sqrt{3}\ \text{})\)。

方法一：\(\overrightarrow{AO}=\lambda\overrightarrow{AD}=\frac{\lambda}{2}(\overrightarrow{AB}+\overrightarrow{AC})=(1-\mu)\overrightarrow{AE}+\mu\overrightarrow{AC}=\frac{1-\mu}{3}\overrightarrow{AB}+\mu\overrightarrow{AC}\)

解方程得 \(\lambda=\frac{1}{2},\mu=\frac{1}{4}\)，\(\overrightarrow{AO}=\frac{1}{4}\overrightarrow{AB}+\overrightarrow{AC},\overrightarrow{EC}=-\frac{1}{3}\overrightarrow{AB}+\overrightarrow{AC}\)。

代入题目，\(\frac{1}{2}AB^2=\frac{3}{2}AC^2,\frac{AB}{AC}=\sqrt{3}\)。

方法二：作 \(AB\) 另一个三等分点 \(F\)，连接 \(DF\) 构造中位线。

平面向量的坐标表示

• 在平面直角坐标系中，设与 \(x\) 轴，\(y\) 轴方向相同的两个单位向量分别为 \(\mathbf{i},\mathbf{j}\)，取 \(\set{\mathbf{i},\mathbf{j}}\) 作为基底，对于平面内任意一个向量 \(\mathbf{a}\)，有且只有一对实数 \(x,y\)，使得 \(\mathbf{a}=x\mathbf{i}+y\mathbf{j},(x,y)\) 就是 \(\mathbf{a}\) 的坐标，记作 \(\mathbf{a}=(x,y)\)。

  显然，\(\mathbf{i}=(1,0),\mathbf{j}=(0,1),\mathbf{0}=(0,0)\)，\(\overrightarrow{OA}=x\mathbf{i}+y\mathbf{j} \Longleftrightarrow A\) 的坐标 \((x,y)\)。

  若表示向量 \(\mathbf{a}\) 的有向线段的起点和终点的坐标分别为 \((x_1,y_1),(x_2,y_2)\)，则 \(\mathbf{a}=(x_2-x_1,y_2-y_1)\)。

• 若 \(\mathbf{a}=(x_1,y_1),\mathbf{b}=(x_2,y_2)\)，则有 \(\mathbf{a}\pm\mathbf{b}=(x_1\pm x_2,y_1\pm y_2),\mathbf{a}\cdot\mathbf{b}=x_1x_2+y_1y_2\)。

  \(\lambda\mathbf{a}=(\lambda x_1,\lambda y_1),|\mathbf{a}|=\sqrt{x_1^2+y_1^2}\)。

  向量 \(\mathbf{a},\mathbf{b}\) 共线 \(\Longleftrightarrow x_1y_2=x_2y_1\)；向量 \(\mathbf{a}\perp\mathbf{b} \Longleftrightarrow x_1y_2=x_2y_1\)。

  \(\theta=\langle\mathbf{a},\mathbf{b}\rangle\implies\cos\theta=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}\implies\) 柯西不等式的二元形式。

笛卡尔斜坐标系

\(x\) 轴与 \(y\) 轴的角度为 \(\theta\ (\theta\neq\frac{\pi}{2})\) 的坐标系。定义平面直角坐标系中的点 \(P(x,y)\)，将 \(P\) 转移到斜坐标系中变成 \(P'(x',y')\) 满足：

\[\begin{cases}x'=x+y\cos\theta \\ y'=y\sin\theta\end{cases}\ 和\ \begin{cases}x=x'-\frac{y'}{\tan\theta} \\ y=\frac{y'}{\sin\theta}\end{cases} \]

于是我们可以把平面向量在平面直角坐标系中的一些运算迁移到斜坐标系中：

• 数量积：\((x_1',y_1')\cdot(x_2',y_2')=x_1x_2+y_1y_2+(x_1y_2+x_2y_1)\cos\theta\)

• 模长：\(\mathbf{a}=(x',y'),|\mathbf{a}|=\sqrt{x^2+y^2+2xy\cos\theta}\)

• 夹角：\(\mathbf{a}=(x_1',y_1'),\mathbf{b}=(x_2',y_2'),\cos\gamma=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}\)

例题：\(\Delta ABC\) 中，\(D,E\) 为 \(BC\) 上的两个三等分点，\(\overrightarrow{AB}\cdot\overrightarrow{AD}=2\overrightarrow{AC}\cdot\overrightarrow{AE}\)，则 \(\cos\angle ADE\) 的最小值为（ \(\frac{4}{7}\) ）。

以 \(\overrightarrow{DC},\overrightarrow{DA}\) 的方向作为平面 \(ABC\) 斜坐标系中 \(x',y'\) 轴的正方向，并设 \(|\overrightarrow{DA}|=m,|\overrightarrow{DC}|=2\)，可得 \(A(0,m),B(-1,0),C(2,0),D(0,0),E(1,0)\)。

于是 \(\overrightarrow{AB}\cdot\overrightarrow{AD}=(-1,-m)\cdot(0,-m)=m^2+m\cos\angle ADE\),\(\overrightarrow{AC}\cdot\overrightarrow{AE}=(2,-m)\cdot(1,-m)=2+m^2-3m\cos\angle ADE\)。

根据题意整理得 \(\cos\angle ADE=\frac{1}{7}(m+\frac{4}{m})\geq\frac{4}{7}\)。

三角形

三角形四心

以下记连接顶点和各交点的直线延长至顶点对边为 \(AD,BE,CF\)，设 \(\Delta ABC\) 的外接圆半径为 \(R\)，\(K\) 为平面内任意一点，\(\lambda,\mu,\eta\in\R^+\)

\(\Delta ABC\)	重心 \(G\)	垂心 \(H\)
交点	中线	高
基本性质	\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0} \\ \overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})\)	\(\overrightarrow{HA}\cdot\overrightarrow{HB}=\overrightarrow{HB}\cdot\overrightarrow{HC}=\overrightarrow{HC}\cdot\overrightarrow{HA}\\AH\cdot HD=BH\cdot HE=CH\cdot CF\)
坐标	\(\displaystyle G(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})\)	\(\displaystyle H\left(\frac{\frac{a}{\cos A}x_1+\frac{b}{\cos B}x_2+\frac{c}{\cos C}x_3}{\frac{a}{\cos A}+\frac{b}{\cos B}+\frac{c}{\cos C}},\frac{\frac{a}{\cos A}y_1+\frac{b}{\cos B}y_2+\frac{c}{\cos C}y_3}{\frac{a}{\cos A}+\frac{b}{\cos B}+\frac{c}{\cos C}}\right)\)
边的向量表示	\(\because\overrightarrow{AG}=\lambda(\overrightarrow{AB}+\overrightarrow{AC}) \\ \therefore\overrightarrow{KG}=\overrightarrow{KA}+\lambda(\overrightarrow{AB}+\overrightarrow{AC})\\=\overrightarrow{KA}+\lambda(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|\sin B}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|\sin C})\)	\(\because \lambda(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|\cos B}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C})\perp\overrightarrow{BC}\\ \text{} \\ \therefore\overrightarrow{KH}=\overrightarrow{KA}+\lambda(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|\cos B}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C})\)
面积	\(S_{\Delta BGC}=S_{\Delta AGC}=S_{AGB}\)	\(S_{\Delta BHC}:S_{\Delta AHC}:S_{\Delta AHB}=\tan A:\tan B:\tan C \\ \tan A\cdot\overrightarrow{HA}+\tan B\cdot\overrightarrow{HB}+\tan C\cdot\overrightarrow{HC}=\overrightarrow{0}\)
定理	\(\\ 中线定理\begin{cases}AD^2=\frac{2b^2+2c^2-a^2}{4}\\ BE^2=\frac{2a^2+2c^2-b^2}{4}\\ CF^2=\frac{2a^2+2b^2-c^2}{4}\end{cases}\\\) 中线长定理（ \(AB \to \overrightarrow{AB}\) ） \(\\ AB^2+AC^2=2AD^2+2DB^2\)
其余等量关系	\(1. \min\set{KA\cdot KB\cdot KC}=GA\cdot GB\cdot GC\\ 2.\) 三角形中势能最小的点为重心，即 \(\\ \begin{aligned}&\mathrm{min}\set{KA^2+KB^2+KC^2}\\&=GA^2+GB^2+GC^2\end{aligned}\) 二者都可用解析几何证明	\(AH=2R|\cos A|\ \ \ \ \ BH=2R|\cos B|\ \ \ \ \ CH=2R|\cos C|\\HD:HE:HF=|\cos B\cos C|:|\cos C\cos A|:|\cos A\cos C|\\ HA^2+BC^2=HB^2+CA^2=HC^2+AB^2\)

\(\Delta ABC\)	内心 \(I\)	外心 \(O\)
交点	内角平分线	垂直平分线
基本性质	\(I\) 到三条边的距离相等 \(\\ \begin{cases}\overrightarrow{IA}\cdot(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}-\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|})=\overrightarrow{0} \\ \overrightarrow{IB}\cdot(\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}-\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|})=\overrightarrow{0} \\ \overrightarrow{IC}\cdot(\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}-\frac{\overrightarrow{CB}}{|\overrightarrow{CA}|})=\overrightarrow{0}\end{cases}\\\) 以上三条公式括号内两向量可互换	\(OA=OB=OC \\ \angle_{AOB}=2\angle_C\ \ \ \ \angle_{AOC}=2\angle_B\ \ \ \ \angle_{BOC}=2\angle_A\\ \begin{cases}\overrightarrow{AO}\cdot\overrightarrow{AB}=\frac{1}{2}|\overrightarrow{AB}|^2 \\ \overrightarrow{AO}\cdot\overrightarrow{AC}=\frac{1}{2}|\overrightarrow{AC}|^2\\ \overrightarrow{BO}\cdot\overrightarrow{BC}=\frac{1}{2}|\overrightarrow{BC}|^2\end{cases}\)
坐标	\(\displaystyle I(\frac{ax_A+bx_B+cx_C}{a+b+c},\frac{ay_A+by_B+cy_C}{a+b+c})\)	\(\displaystyle O\left(\frac{\sin 2Ax_1+\sin 2Bx_2+\sin 2Cx_3}{\sin 2A+\sin 2B+\sin 2C},\frac{\sin 2Ay_1+\sin 2By_2+\sin 2Cy_3}{\sin 2A+\sin 2B+\sin 2C}\right)\)
边的向量表示	\(\begin{aligned}\overrightarrow{AI}&=\lambda(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|})\\&=\mu(\sin B\cdot\overrightarrow{AB}+\sin C\cdot\overrightarrow{AC})\\&=\eta(\frac{\overrightarrow{AB}}{\sin C}+\frac{\overrightarrow{AC}}{\sin B})\end{aligned}\)	\(\overrightarrow{KO}=\frac{\overrightarrow{KB}+\overrightarrow{KC}}{2}+\lambda(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|\cos B}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C}) \\ \text{} \\ \Delta ABC\) 的外心在 \(O\) 点的集合中
面积	\(S_{\Delta BIC}:S_{\Delta AIC}:S_{\Delta AIB}=a:b:c\\a\cdot\overrightarrow{IA}+b\cdot\overrightarrow{IB}+c\cdot\overrightarrow{IC}=\overrightarrow{0}\)	\(S_{\Delta BOC}:S_{\Delta AOC}:S_{\Delta AOB}=\sin 2A:\sin 2B:\sin 2C\\\sin 2A\cdot\overrightarrow{OA}+\sin 2B\cdot\overrightarrow{OB}+\sin 2C\cdot\overrightarrow{OC}=\overrightarrow{0}\)
定理	角平分线定理 $ AD$ 平分 \(\angle BAC \implies \frac{AB}{BD}=\frac{AC}{CD}\\\) 鸡爪定理 \(\\\) \(AI\) 交 \(\Delta ABC\) 外接圆于 \(D\) 有 \(ID=DB=DC\)
其余等量关系	\(|\overrightarrow{BC}|\cdot\overrightarrow{IA}+|\overrightarrow{AC}|\cdot\overrightarrow{IB}+|\overrightarrow{AB}|\cdot\overrightarrow{IC}=\overrightarrow{0} \\ AI:BI:CI=\frac{1}{\sin\frac{A}{2}}:\frac{1}{\sin\frac{B}{2}}:\frac{1}{\sin\frac{C}{2}}\)	\(\begin{cases}\overrightarrow{AO}\cdot\overrightarrow{AD}=\frac{1}{4}(|\overrightarrow{AB}|^2+|\overrightarrow{AC}|^2) \\ \overrightarrow{BO}\cdot\overrightarrow{BE}=\frac{1}{4}(|\overrightarrow{BA}|^2+|\overrightarrow{BC}|^2) \\ \overrightarrow{CO}\cdot\overrightarrow{CF}=\frac{1}{4}(|\overrightarrow{CA}|^2+|\overrightarrow{CB}|^2)\end{cases}\\ \begin{cases}\overrightarrow{AO}\cdot\overrightarrow{BC}=\frac{1}{2}(|\overrightarrow{AC}|^2-|\overrightarrow{AB}|^2) \\ \overrightarrow{BO}\cdot\overrightarrow{AC}=\frac{1}{2}(|\overrightarrow{BC}|^2-|\overrightarrow{BA}|^2) \\ \overrightarrow{CO}\cdot\overrightarrow{AB}=\frac{1}{2}(|\overrightarrow{CB}|^2-|\overrightarrow{CA}|^2)\end{cases}\)

• 内接圆半径 \(r=\frac{\tan\frac{A}{2}(b+c-a)}{2}\)。

• 欧拉定理：\(O,I\) 分别为外接圆、内切圆圆心，则有 \(OI^2=R^2-2Rr\)。

• 欧拉线定理：三角形的外心 \(O\)，垂心 \(H\)，重心 \(G\) 依次位于同一直线上，且重心到外心的距离是重心到垂心的距离的一半，即 \(\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OH}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})\)。

例题：根据欧拉线定理，在 \(\Delta ABC\) 中有 \(AB=2,AC=3\)，以下正确的有（ ACD ）

\(A.\ \overrightarrow{AH}\cdot\overrightarrow{BC}=\overrightarrow{0}\ \ \ \ \ B.\ \overrightarrow{AG}\cdot\overrightarrow{BC}=-\frac{5}{3}\ \ \ \ \ C.\ \overrightarrow{AO}\cdot\overrightarrow{BC}=\frac{5}{2}\ \ \ \ \ D.\ \overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)

对 \(A\)，因为 \(H\) 为垂心，所以 \(AH\perp BC\)，显然正确。

对 \(B\)，\(\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC}),\ \overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\implies\overrightarrow{AG}\cdot\overrightarrow{BC}=\frac{5}{3}\)

对 \(C\)，\(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB},\ \overrightarrow{AO}\cdot\overrightarrow{AB}=\frac{1}{2}|\overrightarrow{AB}|^2,\ \overrightarrow{AO}\cdot\overrightarrow{AC}=\frac{1}{2}|\overrightarrow{AC}|^2\)

对 \(D\)，\(\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OH},\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\implies\overrightarrow{OG}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})=\frac{1}{3}\overrightarrow{OH}\)

三角形面积公式

以下记 \(S\) 为三角形面积，\(r\) 为三角形内切圆半径，\(R\) 为三角形外接圆半径。

• 海伦公式：\(p=\frac{a+b+c}{2},S=\sqrt{p(p-a)(p-b)(p-c)},r=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}\)。

• 利用 \(\sin\)：\(S=\frac{bc\sin A}{2}=\frac{ab\sin C}{2}=\frac{ac\sin B}{2}=\frac{a^2\sin B\sin C}{2\sin A}=\frac{b^2\sin A\sin C}{2\sin B}=\frac{c^2\sin A\sin B}{2\sin C}\)。

• 内切圆：\(S=\frac{r(a+b+c)}{2}\), 外接圆：\(S=2R^2\sin A\sin B\sin C=\frac{abc}{4R}\), 注意可与 正弦定理 连用。

• 多边形面积（ 皮克定理 ）：\(S=a+\frac{b}{2}-1\)，其中 \(a\) 为多边形内部的点数，\(b\) 为多边形落在格点上的点数。

• 等边三角形面积：\(S=\frac{\sqrt{3}}{4}a^2\)，其中 \(a\) 为等边三角形边长。

• 在 \(\Delta ABC\) 中，已知 \(\overrightarrow{AB}=(x_1,y_1), \overrightarrow{AC}=(x_2, y_2)\implies S=\frac{1}{2}|x_1y_2-x_2y_1|\)。

例题 1：已知锐角三角形里 \(B=\frac{\pi}{3},c=2\)，求 \(S\) 范围？

\(\because \frac{a}{\sin A}=\frac{C}{\sin C}\ \ \ \ \ \therefore a=\frac{c\sin A}{\sin C}=\frac{2\sin A}{\sin(\frac{2\pi}{3}-A)}\)

\[S=\frac{ac\sin B}{2}=\frac{\sqrt{3}}{2}\cdot\frac{c\sin A}{\sin C}=\frac{\sqrt{3}}{2}\cdot\frac{2\sin A}{\sin(\frac{2\pi}{3}-A)}=\frac{\sqrt{3}\sin A}{\frac{\sqrt{3}}{2}\cos A+\frac{1}{2}\sin A}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2\tan A}+\frac{1}{2}} \]

\(\because \frac{\pi}{6}<A<\frac{\pi}{2} \ \ \ \ \ \therefore\tan A>\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{2}<\frac{\sqrt{3}}{\frac{\sqrt{3}}{2\tan A}+\frac{1}{2}}<2\sqrt{3}\)

例题 2：\(\Delta ABC\) 中满足 \(4\sqrt{3}S=a^2+b^2+c^2\)，求 \(\frac{2a}{3b+c}\) 的值？

由 \(S=\frac{1}{2}ab\sin C\) 和 \(c^2=a^2+b^2-2ab\cos C\) 得到 \(ab(\sqrt{3}\sin C+\cos C)=a^2+b^2\)

\(\therefore 2\sin(C+\frac{\pi}{6})=\frac{a^2+b^2}{ab}\)

\(\because \frac{a^2+b^2}{ab}\geq\frac{2ab}{ab}=2\) （ 当且仅当 \(a=b\) 时取等 ）

\(\therefore \Delta ABC\) 为等边三角形，\(\frac{2a}{3b+c}=\frac{1}{2}\)

同样的一道练习题：实数 \(a,b,c\) 满足 \(e^{a-b+c}+e^{a+b-c}=2e^2(a-1)\)，求 \(\large(\frac{abc}{a^4+b^4+c^4})_{\max}\)

答案：\(\frac{\sqrt{2}}{8}\)，此时 \(b^4=c^4=8,a=2\)。

求三角形内最值问题

已知 \(\Delta ABC\)，\(D\) 在边 \(BC\) 上。

1. 已知 \(\frac{BD}{CD},AD,\cos\angle_{BAC}\implies\) 向量法，\((\overrightarrow{AD})^2=[x\overrightarrow{AB}+(1-x)\overrightarrow{AC}]^2,S=\frac{1}{2}AB\cdot AC\cdot\sin\angle_{BAC}\)

2. 已知 \(AD\perp BC,AD,\cos\angle_{BAC}\implies\) 正弦定理 + 三角恒等变换，\(AB=\frac{AD}{\sin B},AC=\frac{AD}{\sin C}\)

3. 已知一角一边 \(\implies\) 正弦定理 \(a=\frac{b\sin A}{\sin B}\dots\)

4. 已知 \(AD\) 为角平分线 \(\left[\overrightarrow{AD}=\lambda(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}+\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|})\right]\) 与 \(AB,AC\implies\) 角平分线定理 / 正弦定理 / 面积。

5. 求内切圆半径取值范围 \(r=\frac{2S}{a+b+c}\)

   例：已知 \(c=2,C=60\degree\implies r=\frac{\sqrt{3}}{2}\frac{ab}{a+b+2}\xlongequal{余弦定理}\frac{\sqrt{3}}{6}\frac{(a+b)^2-4}{a+b+2}=\frac{\sqrt{3}}{6}(a+b-2)=\frac{\sqrt{3}}{6}(\frac{c\sin A}{\sin C}+\frac{c\sin B}{\sin C})=\dots\)

立体几何

弧度制与面积计算

• \(360\degree=2\pi\ \text{rad},\ 180\degree=\pi\ \text{rad}\)

• \(1\degree=\frac{\pi}{180}\ \text{rad}\approx0.01745\ \text{rad},1\ \text{rad}=(\frac{180}{\pi})\degree\approx 57.29578\degree\)

• \(x\degree=\frac{x\pi}{180}\ \text{rad},x \ \text{rad}=(\frac{180x}{\pi})\degree\)

• 圆心角大小（ 弧度 ） \(|\alpha|=\frac{l}{r}\ \ \ \ \text{}\) 圆心角大小（ 角度 ） \(n=\frac{180\cdot l}{r\pi}\)

• 弧长 \(l=\alpha r\)，周长 \(C=2r+l\)，面积 \(S=\frac{1}{2}\alpha r^2=\frac{1}{2}lr\)

基本立体图形

• 共性：都具有顶点、底面、侧面、侧棱（ 相邻侧面的公共边 ）。

• 棱柱：有两个面相互平行，其余各面都是四边形，并且相邻两个四边形的公共边都相互平行。底面是 \(n\) 边形就叫 \(n\) 棱柱。斜高：侧面的高。

  侧棱垂直于底面的柱叫做直棱柱，侧棱不垂直于底面的棱柱叫做斜柱。底面是正多边形的直棱柱叫做正棱柱，底面是平行四边形的四棱柱也叫做平行六面体。

  \[\set{正方体}\in\set{正四棱柱}\in\set{长方体}\in\set{直四棱柱} \]

• 棱锥：三棱锥又叫四面体（ 即由四个面组成的封闭图形只能是三棱锥 ），底面是正多边形，并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥。

  正三棱锥 / 正四面体的三条对棱两两垂直。

• 棱台：棱锥上部通过平行于底面的面截取上部且上下底面平行。

• 圆柱 / 圆锥 / 圆台：旋转轴称为它的轴，平行于轴的边叫做它侧面的母线。

• 欧拉公式：\(V-E+F=2\)，即 顶点数 \(-\) 棱数 \(+\) 面数 \(=2\)。

  对于正 \(n\) 面体（ \(n\) 个等边三角形 ），面数为 \(n\)，棱数为 \(\frac{3}{2}n\)（ 每个面 \(3\) 条棱，每条棱分属 \(2\) 个面 ）。

立体图形的直观图

• 斜二测画法

  \(\angle xOy=90\degree\xLeftrightarrow{x\ 轴不变}\angle x'Oy'=45\degree\) 或 \(135\degree,\angle x'Oz'=\angle xOz=90\degree\)，\(\\\) 原来平行于 \(x\) 轴 或 \(z\) 轴 的线段，在直观图中保持原长度不变，原来平行于 \(y\) 轴的线段，在直观图中长度变为原来的一半。

• \(S_{直}=\frac{\sqrt{2}}{4}S_{原},S_{原}=2\sqrt{2}S_{直}\)

简单几何体的表面积和体积

下表中 \(r\) 为底面半径，\(l\) 为母线长，\(h\) 为高，\(C\) 为底面周长；特别地，台体 \(S\) 与 \(S'\) 分别代表上下底面面积，\(r\) 与 \(r'\) 同理。\(\\\)
棱锥侧面积计算公式中，\(a\) 代表底面边长，\(h'\) 为斜高。棱台侧面积计算公式中，\(C'',C'\) 分别代表上下底面周长，\(h''\) 代表斜高。

几何体	表面积	体积	侧面积
棱柱	围成它们的各个面面积之和	\(V=Sh\)	\(S_{直棱柱侧}=Ch\)
棱锥	围成它们的各个面面积之和	\(V=\frac{1}{3}Sh\)	\(S_{正\ n\ 棱锥侧}=\frac{1}{2}nah'\)
棱台	围成它们的各个面面积之和	\(V=\frac{1}{3}h(S'+\sqrt{S'S}+S)\)	\(S_{正棱台侧}=\frac{1}{2}(C''+C')h''\)
圆柱	\(S=2\pi r(r+l)\)	\(V=Sh=\pi r^2h\)	\(S_{圆柱侧}=2\pi rl\)
圆锥	\(S=\pi r(r+l)\)	\(V=\frac{1}{3}Sh=\frac{1}{3}\pi r^2h\)	\(S_{圆锥侧}=\pi rl\)
圆台	\(S=\pi(r'^2+r^2+r'l+rl)\)	\(\begin{aligned}V&=\frac{1}{3}h(S'+\sqrt{S'S}+S)\\&=\frac{1}{3}\pi h(r'^2+r'r+r^2)\end{aligned}\)	\(S_{圆台侧}=\pi(r+r')l\)
球	\(S=4\pi r^2\)	\(V=\frac{4}{3}\pi r^3\)	/

• 祖暅原理：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等。

• 画展开图类问题：绳绕棱锥 / 圆锥，先求出展开图圆心角的度数（ 大概率 \(90\degree\) ）

  例 1：在正四棱锥 \(O-ABCD\) 中，侧棱长均为 \(4\)，且相邻两条侧棱的夹角为 \(30\degree\)，\(E,F\) 分别为线段 \(OB,OC\) 上的一点，则 \(AE+EF+FD\) 的最小值为 ？（ \(4\sqrt{2}\) ）

  例 2：一个圆台的上、下底面半径分别为 \(5,10\)，母线 \(AB=20\)，从圆台母线 \(AB\) 的中点 \(M\) 拉一条绳子绕圆台侧面转到 \(A\)，求绳子的最短长度（ \(50\) ）和上底面圆周上的点到绳子的最短距离（ \(4\) ）。

• 射影问题：三棱锥 \(P-ABC\) 中，\(O\) 为 \(P\) 在平面 \(ABC\) 内的射影，则：

\(O\) 为外心	\(O\) 为内心	\(O\) 为垂心
\(1. PA=PB=PC \\ 2. PA,PB,PC\) 与平面 \(ABC\) 所成角相等	\(1. P\) 到 \(\Delta ABC\) 各边距离相等 \(\\ 2.\) 三侧面与底面所成二面角相等	\(1. PA\perp PB,PB\perp PC,PA\perp PC \\ 2. PA \perp BC,PB\perp AC, PC\perp AB \\\)（ 三组对棱互相垂直 ）

球与几何体的外接、内切问题

• 外接球：多面体 / 旋转体的顶点均在球面上，球心到各个顶点的距离相等，球心在旋转轴上。

  注意 球心可能在几何体外。

• 内切球：多面体 / 旋转体的各面均与球面相切，球心到各面的距离相等，球心在旋转轴上。

  利用等体积法求半径（ \(V=\frac{1}{3}S_表 r\) ），再求每个面面积，最后 \(\boxed{各个棱锥的体积之和 = 多面体体积}\implies\) 内切球半径。

  例 1：若三棱锥的三条侧棱两两垂直，且长度均为 \(2\)，则三棱锥外接球半径 \(R=\frac{\sqrt{2^2+2^2+2^2}}{2}=\sqrt{3}\)。

  例 2：若三棱锥 \(P-ABC\) 的三条侧棱两两垂直，\(AB=\sqrt{5},BC=\sqrt{7},AC=2\)，则此三棱锥的外接球的体积为 ？

  \(2R=\sqrt{PA^2+PB^2+PC^2}=\sqrt{\frac{1}{2}(AC^2+AB^2+BC^2)}=2\sqrt{2},R=\sqrt{2},V=\frac{4}{3}\pi R^3=\frac{8\sqrt{2}}{3}\pi\)

• 球内接正三棱锥的体积最大值 \(=\) 球内接正四面体的体积。

  球内接正四棱锥的体积最大值 \(=\) 一个底面边长 \(=\) 高的正四棱锥的体积。

几何体	外接球半径 \(R\)	外接球球心	内切球半径 \(r\)
长方体	\(2R=\sqrt{a^2+b^2+c^2}\)	体对角线的中点
正方体	\(R=\frac{\sqrt{3}}{2}a\)	体对角线的中点	$r=\frac{a}{2} \ $ 与正方体各棱相切的球 \(\\\) 叫做棱切球，半径 \(\frac{\sqrt{2}a}{2}\)
直棱柱 / 圆柱	\(R^2=(\frac{h}{2})^2+r^2\\ r\) 为底面外接圆半径 \(\\\) 可利用正弦定理求	上下底面中心连线的中点
侧棱与底面 \(\\\) 垂直的锥体	\(R^2=(\frac{h}{2})^2+r^2\\ r\) 为底面外接圆半径 \(\\\) 可利用正弦定理求	过底面外接圆圆心 \(\\\) 且垂直于底面的直线 \(\\\) 与垂直于底面的侧棱 \(\\\) 的中垂面的交点
正棱锥 / 圆锥	\(R^2=(R-h)^2+r^2\\ \implies R=\frac{h^2+r^2}{2h}\\ r\) 为底面外接圆半径 \(\\\) 可利用正弦定理求	正棱锥 / 圆锥顶点与 \(\\\) 底面外心连线 / 延长线上
正四面体 \(\\\) 高 \(\frac{\sqrt{6}a}{3}\\\) 体积 \(\frac{\sqrt{2}}{12}a^3\)	\(R=\frac{\sqrt{6}}{4}a \\ a\) 为其棱长 \(\\\) 也可用长方体的公式		\(r=\frac{\sqrt{6}}{12}a \\ a\) 为其棱长

• 若某一几何体的表面积为 \(S\)，体积为 \(V\)，内切球半径为 \(r\)，则满足 \(V=\frac{1}{3}Sr\)。

• 将四面体补形成长方体的条件（ 满足其中之一即可 ）：

  1. 有三条棱两两垂直。
  2. 四个面均是直角三角形。
  3. 正四面体 \(P-ABC\) 可以补形成正方体且棱长 \(a=\frac{PA}{\sqrt{2}}\)。
  4. 三组对棱分别相等，长度记为 \(x,y,z\)，长方体边长记为 \(a,b,c\)，则 \(\begin{cases} x=\sqrt{a^2+b^2} \\ y=\sqrt{b^2+c^2} \\ z=\sqrt{a^2+c^2} \end{cases}\)

空间点、直线、平面之间的关系

• 平面的表示：用横向 / 竖向的平行四边形表示，书写方法：平面 \(\alpha,\beta,\gamma\dots\) 或 平面 \(ABCD\)，平面 \(AC,BD\)。

四个基本事实与三个推论

• 基本事实

  1. 过不在 同一直线上 的三个点，有且只有一个平面。即不共线的三点确定一个平面。

     一条直线与直线外一点也能确定一个平面。

     在同一平面内，\(n\) 条直线最多把平面划分为 \(1+\frac{n(n-1)}{2}\) 份；在空间内，\(n\) 个平面最多把空间分为 \(\frac{n^3+5n+6}{6}\) 份。

     相交于同一点的 \(n\) 条直线最多可以确定 \(\begin{cases}\frac{n(n-1)}{2}\ 个平面 & 任意\ 3\ 条不共面 \\ \frac{(n-3)(n-4)}{2}\ 个平面 & 有\ 3\ 条不共面 \end{cases}\)

  2. 如果一条直线上的两个点在同一平面内，那么这条直线在这个平面内。即：

     直线 \(l\) 在 \(\alpha\) 内 \(\xLeftrightarrow{}l\subset\alpha\ \ \ \ \text{}\) 直线 \(l\) 不在 \(\alpha\) 内 \(\xLeftrightarrow{}l\not\subset\alpha\)

     基本事实 2 用符号表示为：\(A\in l,B\in l\) 且 \(A\in\alpha,B\in\alpha\implies l\subset\alpha\)

  3. 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

     平面 \(\alpha\) 与 \(\beta\) 相交于直线 \(l\)，记作 \(\alpha\bigcap\beta=l\)。

     基本事实 3 用符号表示为：\(P\in\alpha\) 且 \(P\in\beta\implies\alpha\bigcap\beta=l\) 且 \(P\in l\)

  4. 平行于同一条直线的两条直线平行。（ 平行线的传递性 ）

  注意表示 点 在 直线 / 平面 内用 \(\in\)，表示 直线 在 平面 内用 \(\subset\)。

• 推论（ 基本事实 1 + 2 + 两点确定一条直线 ）

  1. 经过一条直线和这条直线外一点，有且只有一个平面。
  2. 经过两条相交直线，有且只有一个平面。
  3. 经过两条平行直线，有且只有一个平面。

空间点、直线、平面之间的位置关系

\[直线与直线\begin{cases}共面直线\begin{cases}相交直线：在同一平面内，有且只有一个公共点 \\ 平行直线：在同一平面内，没有公共点\end{cases} \\ 异面直线：不同在任何一个平面内，没有公共点\end{cases} \]

\[直线与平面\begin{cases}直线在平面内 \ \ \ \ \ \ \ \ 有无数个公共点 \\ \begin{rcases}直线与平面相交 & 有且只有一个公共点 \\ 直线与平面平行 & 没有公共点\end{rcases} 直线在平面外 \end{cases} \]

\[直线\ a\ 与平面\ \alpha\ 相交于点\ A，记作a\bigcap\alpha=A\ \ \ \ \ 直线\ a\ 与平面\ \alpha\ 平行，记作\ a//\alpha \]

\[平面与平面\begin{cases}两个平面平行 & 没有公共点 \\ 两个平面相交 & 有一条公共直线\end{cases} \]

\[平面\ \alpha\ 与平面\ \beta\ 平行，记作\ \alpha//\beta \]

证明共面、共线、共点

1. 证明点、线共面：证明直线平行 / 相交；确定一个辅助平面；反证法。
2. 证明三点共线：先找 \(2\) 个平面，证明这 \(3\) 点都是 \(2\) 个平面公共点 / 其中 \(2\) 点确定 \(1\) 条直线，证另一点也在直线上。
3. 证明三线共点：先证明两条直线交于一点，再证明第三条直线经过这个点或交点在第三条直线上。

注意梯形两腰必交于一点；在空间中，不能用两组对边分别相等证明平行四边形。

例题：已知正方体 \(ABCD-A_1B_1C_1D_1\)，\(M,N\) 为棱 \(A_1B_1,B_1C_1\) 中点，求证：\(\\ \ \ \ \ \ (1)\) 直线 \(AM,CN\) 共面； \(\\ \ \ \ \ \ (2)\) 直线 \(D_1B\) 和 \(CC_1\) 是异面直线。

\(pf:(1)AA_1 \parallel CC_1,AA_1=CC_1\implies\) 四边形 \(ACC_1A_1\) 是平行四边形。

\(\ \ \ \ \ \ AC\parallel A_1C_1\parallel MN \implies\) 直线 \(AM,CN\) 共面。

\(\ \ \ \ \ \ \ (2)\) 反证法，假设四点共面于 \(\alpha\)，则 \(B,C,C_1\) 可以确定一个平面 \(BC_1\)，这两个平面重合，又因为 $D_1B \sub $ 平面 \(BC_1\)，所以 \(D_1\in\) 平面 \(BC_1\)，与 \(D_1\notin\) 平面 \(BC_1\) 矛盾，故原假设错误。

空间直线、平面的平行

1. 等角定理：如果空间中两个角的两条边分别对应平行，那么两个角相等或互补。

2. 直线与平面平行的判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

   用符号表示：\(a\not\subset\alpha,b\subset\alpha,a//b\implies a//\alpha\)

3. 直线与平面平行的性质定理：一条直线与一个平面平行，如果过该直线的平面与此平面相交，那么该直线与交线平行。

   用符号表示：\(a//\alpha,\alpha\bigcap\beta=b,a\subset\beta\implies a//b\)

4. 平面与平面平行的判定定理：如果一个平面内的 两条相交直线 与另一个平面平行，那么这两个平面平行。

   用符号表示：\(a\subset\beta,b\subset\beta,a\bigcap b=P,a//\alpha,b//\alpha\implies\alpha//\beta\)

5. 平面与平面平行的性质定理：两个平面平行，如果另一个平面与这两个平面相交，那么两条交线平行。

   用符号表示：\(\alpha//\beta,\alpha\bigcap\gamma=a,\beta\bigcap\gamma=b\implies a//b\)

可简记为：线线平行 \(\xLeftrightarrow{}\) 线面平行 \(\implies\) 面面平行 \(\implies\) 线线平行，恰好形成一个循环。

空间直线、平面的垂直

• 直线与平面垂直的判定定理：如果一条直线与一个平面内的 两条相交直线 垂直，那么该直线与此平面垂直。

  用符号表示：\(m\subset\alpha,n\subset\alpha,m\bigcap n=P,l\perp m,l\perp n\implies l\perp\alpha\)

• 直线与平面垂直的性质定理：垂直于同一个平面的两直线平行。

• 平面与平面垂直的判定定理：如果一个平面过另一个平面的垂线，那么这两个平面垂直。

  用符号表示：\(a\subset\alpha,a\perp\beta\implies\alpha\perp\beta\)

• 平面与平面垂直的性质定理：两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直。

空间直线、平面的平行

1. 三棱锥 \(P-ABC\) 中，\(D,E\) 分别是 \(PB,BC\) 中点，点 \(F\) 在线段 \(AC\) 上，且满足 $AD // $ 平面 \(PEF\)，则 \(\frac{AF}{FC}=\ ?\)

   

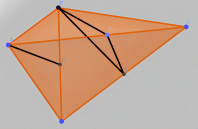
   解析：连接 \(CD\)，交 \(PE\) 于点 \(G\)，连接 \(FG\)，如图所示。

   

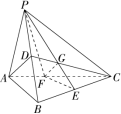
   \(AD //\) 平面 \(PEF\)， 平面 \(PEF\ \cap\) 平面 \(ADC=FG\implies AD // FG\)

   \(D,E\) 分别是 \(PB,BC\) 中点 \(\implies G\) 是 \(\Delta PBC\) 重心，\(\frac{AF}{FC}=\frac{DG}{GC}=\frac{1}{2}\)。

---

2. 长方体 \(ABCD-A_1B_1C_1D_1,AB=BC,E\) 是 \(AB\) 上靠近 \(B\) 的三等分点，\(F\) 是 \(A_1D_1\) 中点，\(\\ O\) 为直线 \(DB_1\) 与平面 \(EFC\) 交点，\(\frac{DO}{OB_1}=\ ?\)

   

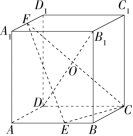
   解析：连接 \(BD,B_1D_1,BD \cap CE=M\)，\(\\\) 设平面 \(CEF\) 与平面 \(A_1B_1C_1D_1\) 的交线交 \(C_1D_1,B_1D_1,A_1B_1\) 分别于点 \(P,N,Q\)，如图所示。

   

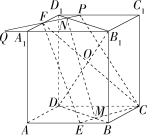
   \(CE // PQ \implies \angle PFD_1=\angle BCE \implies \mathrm{Rt}\Delta PFD_1 \backsim \mathrm{Rt}\Delta ECB,\frac{PD_1}{FD_1}=\frac{EB}{BC}=\frac{1}{3}\)

   \(QA_1=PD_1=\frac{1}{3}FD_1=\frac{1}{6}A_1B_1\implies\frac{B_1N}{ND_1}=\frac{B_1Q}{PD_1}=7\)

   \(\frac{DM}{MB}=\frac{DC}{EB}=3\implies DM=\frac{3}{4}BD\implies\frac{DO}{OB_1}=\frac{DM}{NB_1}=\frac{6}{7}\)

---

3. 四棱锥 \(P-ABCD\) 的底面是边长为 \(1\) 的正方形，\(E\) 是 \(PD\) 上一点满足 \(PE=3ED\)，\(\\\) 若 \(\overrightarrow{PF}=\lambda\overrightarrow{PC}\) 且 \(BF//\) 平面 \(AEC\)，则 \(\lambda=\) ？

   

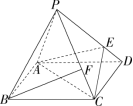
   解析：连接 \(BD\) 交 \(AC\) 于点 \(O\)，连接 \(OE\)，在 \(PD\) 上取一点 \(G\) 使得 \(GE=ED\)。

   

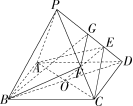
   在 \(\Delta BGD\) 中 \(EO\) 为其中位线 \(\implies BG//\) 平面 \(AEC\implies\) 平面 \(BFG\ //\) 平面 \(AEC\)。

   \(\frac{PF}{FC}=\frac{PG}{GE}=2,\lambda=\frac{2}{3}\)

---

4. 在长方体 \(ABCD-A_1B_1C_1D_1\) 中，\(AD=DD_1=1,AB=\sqrt{3},E,F,G\) 分别是 \(AB,BC,C_1D_1\) 的中点，点 \(P\) 在平面 \(ABCD\) 内，若直线 \(D_1P\ //\) 平面 \(EFG\)，则点 \(D_1\) 与满足题意的点 \(P\) 构成的平面截长方体所得的截面的面积为 ？

   

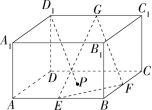
   解析：

   

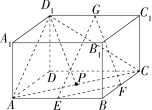
   只需证明点 \(D_1\) 与满足题意的点 \(P\) 构成的平面 \(D_1AC\) 平行于平面 \(EFG\) 即可，答案即为 \(S_{\Delta D_1AC}=\frac{\sqrt{7}}{2}\)。

---

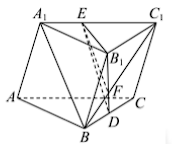
5. 如图，三棱柱 \(ABC-A_1B_1C_1\) 中，\(D\) 是 \(B_1C_1\) 中点，\(E\) 是 \(A_1C_1\) 上一点满足 \(A_1B//\) 平面 \(B_1DE\)，\(\frac{A_1E}{EC_1}=\ ?\)

   

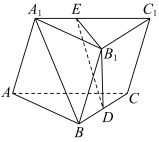
   解析：连接 \(BC_1\) 交 \(B_1D\) 于 \(F\)，易证 \(\Delta A_1BC_1 \backsim \Delta EFC_1,\frac{A_1E}{EC_1}=\frac{BF}{FC_1}=\frac{BD}{B_1C}=\frac{1}{2}\)。

   

空间直线、平面的垂直

1. 如图，\(P\) 是 \(\Delta ABC\) 所在平面外一点，\(PA\perp\) 平面 \(ABC,\angle ABC=90\degree,AE\perp PB\) 于 \(E,AF\perp PC\) 于 \(F.\\\) 求证：\((1)\ BC\perp\) 平面 \(PAB \\ \ \ \ \ \ \ \ \ \ \ (2)\ AE\perp\) 平面 \(PBC \\ \ \ \ \ \ \ \ \ \ \ (3)\ PC\perp\) 平面 \(AEF\)

   

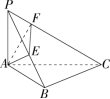
   解析：\((1)\ \angle ABC=90\degree\implies BC\perp AB\ \ \ \ \ \ \ PA\perp\) 平面 \(ABC\implies BC\perp PA\\ \ \ \ \ \ \ \ \ \ \ (2)\ BC\perp\) 平面 \(PAB\implies AE\perp BC\\ \ \ \ \ \ \ \ \ \ \ (3)\ AE\perp\) 平面 \(PBC\implies PC\perp AE\)

定理 & 二级结论

• 三垂线定理：如果平面内的一条直线与平面外的一条斜线在该平面内的射影垂直，那么它也和这条斜线垂直。

  逆定理：如果平面内一直线和这个平面外的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直。

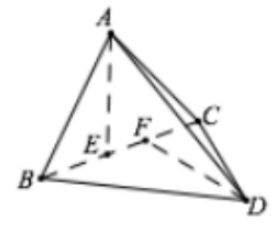
• 空间第一余弦定理：如图，\(AE\perp BC,DF\perp BC\)，则二面角 \(A-BC-D\) 的大小 \(\theta\) 满足

  \[\cos\theta=\frac{AE^2+EF^2+FD^2-AD^2}{2AE\cdot FD} \]

• 空间第二余弦定理：空间中两直线 \(AB,CD\) 的夹角 \(\theta\) 满足 \(\cos\theta=\frac{|AD^2+BC^2-AC^2-BD^2|}{2AB\cdot CD}\)

  证明：\(\overrightarrow{AC}\cdot\overrightarrow{BD}=\overrightarrow{AC}\cdot(\overrightarrow{AD}-\overrightarrow{AB})=|\overrightarrow{AC}||\overrightarrow{AD}|\cos\angle_{CAD}-|\overrightarrow{AC}||\overrightarrow{AB}|\cos\angle_{CAB}=AC\cdot AD\cdot \frac{AC^2+AD^2-CD^2}{2AC\cdot AD}-AC\cdot AB\cdot\frac{AC^2+AB^2-BC^2}{2AC\cdot AB}=\frac{AD^2+CB^2-AB^2-CD^2}{2}\)

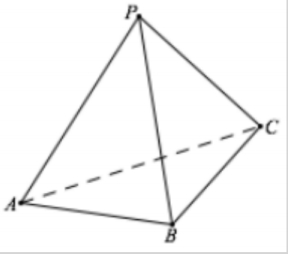
• 三面角公式求二面角：已知 \(\angle_{APB}=\theta_1,\angle_{BPC}=\theta_2,\angle_{APC}=\theta_3\)，则二面角 \(A-PB-C\) 的余弦值为

  \[\cos\theta=\frac{\cos\theta_3-\cos\theta_1\cos\theta_2}{\sin\theta_1\sin\theta_2}=\frac{\cos\angle_{APC}-\cos\angle_{APB}\cdot\cos\angle_{BPC} }{\sin\angle_{APB}\cdot\sin\angle_{BPC} } \]

  注意三个角度在公式中分布特点，\(\theta_3\) 是二面角 \(A-PB-C\) 的对角，而 \(\theta_1,\theta_2\) 就是二面角 \(A-PB-C\) 的两个邻角

• 三正弦定理：二面角 \(M-AB-N\) 的度数为 \(\alpha\)，平面 \(M\) 上有一射线 \(AC\) 与 \(AB\) 所成角为 \(\beta\)，与平面 \(N\) 所成角为 \(\gamma\)，则 \(\sin\gamma=\sin\alpha\sin\beta\)。

• 三余弦定理 / 最小角定理：设 \(A\) 为平面 \(\alpha\) 上一点，过点 \(A\) 的斜线 \(AO\) 在平面 \(\alpha\) 上的射影为 \(AB\)，\(AC\) 为平面 \(\alpha\) 内的一条直线，那么有 \(\cos\angle OAC=\cos\angle BAC\times\cos\angle OAB\)。

证明：\(\cos\angle OAC=\frac{AC}{AO}\ \ \ \ \cos\angle BAC=\frac{AC}{AB}\ \ \ \ \cos\angle OAB=\frac{AB}{AO}\)

即斜线与射影所成的角是斜线与平面内的任何直线所成的角中最小的角。

• 异面直线段 \(AB=a,CD=b\)，它们之间的距离为 \(d\)，夹角为 \(\theta\)，则 \(V_{A-BCD}=\frac{1}{6}abd\sin\theta\)。

• 面积余弦定理：\(\Delta ABC\) 在平面 \(\alpha\) 内的射影为 \(\Delta ABO\)，记 \(\Delta ABC\) 所在平面与 \(\alpha\) 所称的锐二面角为 \(\theta\)，则 \(S_{\Delta ABO}=\cos\theta S_{\Delta ABC}\)。

翻折问题

• 不在同一平面的两点路径问题的翻折只能以折点所在直线翻折。

例：长方体 \(ABCD-A_1B_1C_1D_1\) 中，\(AB=1,AD=2,AA_1=3,P\) 是线段 \(B_1C\) 上一动点，求 \(AP+PD_1\) 的最小值 ？

画出直观图后，应将平面 \(AB_1C\) 和平面 \(B_1CD_1\) 翻折到同一平面上，显然 \(AB_1D_1C\) 是平行四边形。

根据平行四边形中对角线平分和 \(=\) 四条边平方和可得 \((AP+PD_1)_{\min}=AD_1=\sqrt{17}\)。

• 注意分类讨论

例：直三棱柱 \(ABC-A_1B_1C_1\) 中，\(E,F\) 分别为 \(AA_1,C_1B_1\) 的中点，沿棱柱的表面从 \(E\) 到 \(F\) 两点的最短路径的长度是 ？

分三类讨论：

1. 沿 \(BB_1\) 展开，算得 \(EF=\frac{\sqrt{22}}{2}\)。
2. 沿 \(A_1C_1\) 展开，算得 \(EF=\frac{3\sqrt{2}}{2}\)。
3. 沿 \(A_1B_1\) 展开，算得 \(EF=\sqrt{\frac{7}{2}+\sqrt{2}}\)。

于是 \(EF_{\min}=\frac{3\sqrt{2}}{2}\)。

截面问题

1. 求过圆锥顶点的截面面积最大值：记轴截面顶角为 \(\theta\)，\(\sin\theta=\frac{r}{l}\) \(\begin{cases}\theta>\frac{\pi}{2},S_{\max}=\frac{1}{2}l^2\sin\theta\implies\frac{1}{2}l^2 \\ \theta\leq\frac{\pi}{2},S_{\max}=\ 轴截面面积 \end{cases}\)

2. 正方体棱长为 \(1\)，每条棱所在直线与平面 \(\alpha\) 所称角相等，则 \(\alpha\) 截此正方体所得截面面积最大值 ？

注意正方体截面可以是 \(3,4,5,6\) 边形，最大面积是 \(\frac{3\sqrt{3}}{4}\)。

例题：在棱长为 \(2\) 的正方体 \(ABCD-A_1B_1C_1D_1\) 中，\(E\) 为棱 \(AA_1\) 中点，点 \(F\) 在 \(A_1B_1\) 上且满足 \(\overrightarrow{A_1F}=\lambda\overrightarrow{A_1B_1}\)，以下正确的有（ \(\text{ACD}\) ）

\(\text{A.}\) 当 \(\lambda=0\) 时，\(AC_1\perp\) 平面 \(BDF\)。

\(\text{B.}\) \(\forall\lambda\in[0,1],V_{F-BDE}\) 不变。

\(\text{C.}\) \(\exist\lambda\in[0,1]\)，直线 \(AC\) 与平面 \(BDF\) 所成角为 \(\frac{\pi}{3}\)。

\(\text{D.}\) 当 \(\lambda=\frac{2}{3}\) 时，平面 \(BDF\) 截正方体外接球所得截面面积为 \(\frac{56}{19}\pi\)。

选项 \(\text{D}\) 解析：

首先把平面补全为 \(BDGF\)，其中 \(G\) 为棱 \(A_1D_1\) 上靠近 \(D_1\) 的三等分点。

连接 \(A_1C_1\) 与 \(GF,B_1D_1\) 分别交于点 \(P,Q\)，连接 \(AC\) 与 \(BD\) 交于点 \(E\)，连接 \(PE\)。

显然正方体外接球球心 \(O\) 为线段 \(QE\) 中点，记截面所在圆的圆心为 \(O_1\)，则 \(OO_1\perp\) 平面 \(BDF\)。

因为 \(P,E\) 均为对角线上的点，所以 \(O_1\) 在线段 \(PE\) 上。

于是 \(\text{Rt}\Delta PQE \sim \text{Rt} \Delta OO_1E\)，可算得 \(PQ=\frac{\sqrt{2}}{3},PE=\frac{\sqrt{38}}{3},OO_1=\frac{1}{\sqrt{19}}\)。

正方体外接球半径 \(R=\sqrt{3}\)，截面圆半径 \(r=\sqrt{R^2-OO_1^2}=\frac{2\sqrt{266}}{19},S=\pi r^2=\frac{56}{19}\pi\)。

空间向量

基本运算同平面向量。

• \(\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}\) 且 \(x+y+z=1,A,B,C\) 不共线，\(O\not\subset\) 平面 \(ABC\implies A,P,B,C\) 四点共面。

证明：

\[\overrightarrow{AP}=m\overrightarrow{AC}+n\overrightarrow{AB}=\overrightarrow{OP}-\overrightarrow{OA}=m(\overrightarrow{OC}-\overrightarrow{OA})+n(\overrightarrow{OB}-\overrightarrow{OA})=(1-m-n)\overrightarrow{OA}+n\overrightarrow{OB}+m\overrightarrow{OC} \]

• 若 \(\Delta ABC\) 重心为 \(G\)，\(O\) 为 \(\Delta ABC\) 平面外一点，则 \(\overrightarrow{OG}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})\)。

• 法向量：垂直于平面 \(\alpha\) 的向量，有无数多个；怎么求：设法向量为 \((x,y,z)\)，求出平面内两个向量的坐标表示，点乘列方程组求。

• 速求法向量：已知平面 \(\alpha\) 上的两个向量 \(\overrightarrow{a}=(x_1,y_1,z_1),\overrightarrow{b}=(x_2,y_2,z_2)\)，则平面的一个法向量为 \((\begin{vmatrix}y_1 & z_1 \\ y_2 & z_2\end{vmatrix},\begin{vmatrix}z_1 & x_1 \\ z_2 & x_2\end{vmatrix},\begin{vmatrix}x_1 & y_1 \\ x_2 & y_2\end{vmatrix})=(y_1z_2-y_2z_1,z_1x_2-z_2x_1,x_1y_2-x_2y_1)\)。

  相当于求向量叉乘。

• 对称问题

  \((a,b,c)\) 关于什么对称，什么就不变。

  原点 \(O\)	\(x\) 轴	\(y\) 轴	\(z\) 轴	\(Oxy\) 平面	\(Oyz\) 平面	\(Oxz\) 平面
  \((-a,-b,-c)\)	\((a,-b,-c)\)	\((-a,b,-c)\)	\((-a,-b,c)\)	\((a,b,-c)\)	\((-a,b,c)\)	\((a,-b,c)\)

平面方程

• 过 \(P(x_0,y_0,z_0)\) 且法向量 \(\overrightarrow{m}=(A,B,C)\) 的平面方程为 \(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)。

• 过 \(P(x_0,y_0,z_0)\) 且方向向量 \(\overrightarrow{n}=(u,v,w)\) 的直线 \(l\) 的方程为 \(\frac{x-x_0}{u}=\frac{y-y_0}{v}=\frac{z-z_0}{w}\ (uvw\neq 0)\)。

用空间向量研究距离、夹角问题

1. 点线距 —— 求点 \(A\) 到直线 \(BC\) 的距离。

   \(\overrightarrow{a}=\overrightarrow{BA},\overrightarrow{u}=\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|},d=\sqrt{\overrightarrow{a}^2-(\overrightarrow{a}\cdot\overrightarrow{u})^2}\)

2. 点面距 / 线面距 / 面面距 —— 求点 \(A\) 到平面 \(BCD\) 的距离。

   1. 等体积法，\(V_{A-BCD}=V_{B-ACD}=V_{C-ABD}=V_{D-ABC}\)
   2. 求平面 \(BCD\) 的法向量 \(\overrightarrow{n},d=\frac{|\overrightarrow{BA}\cdot\overrightarrow{n}|}{|\overrightarrow{n}|}\)
   3. \(A(x_0,y_0,z_0)\)，平面的解析式 \(Ax+By+Cz+D=0,d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}\)

3. 线线角 —— 求 \(AB,CD\) 夹角 \(\theta\)

   1. 求出它们的方向向量 \(\overrightarrow{u},\overrightarrow{v}\)，则 \(\cos\theta=\frac{\overrightarrow{AB}\cdot\overrightarrow{CD}}{|\overrightarrow{AB}||\overrightarrow{CD}|}=\frac{|\overrightarrow{u}\cdot\overrightarrow{v}|}{|\overrightarrow{u}||\overrightarrow{v}|}\)
   2. 空间第二余弦定理 \(\cos\theta=\frac{|AD^2+BC^2-AC^2-BD^2|}{2AB\cdot CD}\)

4. 线面角 —— \(\sin\theta=\frac{|\overrightarrow{u}\cdot\overrightarrow{n}|}{|\overrightarrow{u}||\overrightarrow{n}|}\) ，较难做的题目亦可用等体积法。

5. 二面角 —— \(\cos\theta=\frac{|\overrightarrow{n_1}\cdot\overrightarrow{n_2}|}{|\overrightarrow{n_1}||\overrightarrow{n_2}|}\)

两直线所成角	异面直线所成角	线面角	平面与平面的夹角	二面角	向量夹角	倾斜角
\([0,\frac{\pi}{2}]\)	\((0,\frac{\pi}{2}]\)	\([0,\frac{\pi}{2}]\)	\([0,\frac{\pi}{2}]\)	\([0,\pi]\)	\([0,\pi]\)	\([0,\pi)\)

向量叉乘

• 若 \(\overrightarrow{a}=a_x\overrightarrow{i}+a_y\overrightarrow{j}+a_z\overrightarrow{k}\)，\(\overrightarrow{b}=b_x\overrightarrow{i}+b_y\overrightarrow{j}+b_z\overrightarrow{k}\)，则 \(\overrightarrow{c}=\overrightarrow{a}\times\overrightarrow{b}=\begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}\)

叉乘的结果是向量，该向量的模值与 \(\overrightarrow{a},\overrightarrow{b}\) 构成的平行四边形面积相等，即 \(|\overrightarrow{a}\times\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}||\sin\theta|=x_1y_2-x_2y_1\)。

该向量的方向垂直于 \(\overrightarrow{a},\overrightarrow{b}\) 构成的平面，用右手螺旋性质确定。

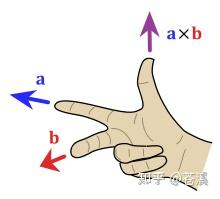
运算特性：\(\begin{cases} \overrightarrow{a}\times\overrightarrow{b}=-\overrightarrow{b}\times\overrightarrow{a} \\ \overrightarrow{a}\times\overrightarrow{a}=\overrightarrow{0} \\ \overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\times\overrightarrow{b}+\overrightarrow{a}\times\overrightarrow{c} \\ (\overrightarrow{a}\times\overrightarrow{b})\times\overrightarrow{c}=(\overrightarrow{a}\cdot\overrightarrow{c})\overrightarrow{b}-(\overrightarrow{b}\cdot\overrightarrow{c})\overrightarrow{a} \end{cases}\)

直线和圆的方程

倾斜角：\(x\) 轴正向与直线 \(l\) 向上的方向之间所成的角 \(\alpha\)。

斜率：\(k=\tan\alpha=\frac{y_2-y_1}{x_2-x_1}\)。

\[l_1\perp l_2\implies k_1\cdot k_2=0,|\alpha_1-\alpha_2|=90\degree \]

直线的一般式方程：\(Ax+By+C=0\implies\) 斜截式方程 \(y=-\frac{A}{B}x-\frac{C}{B}\implies\) 该直线的方向向量 \(\overrightarrow{u}=(B,-A)\)，法向量 \(\overrightarrow{n}=(A,B)\)。

点到直线距离公式：\(\displaystyle \boxed{d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}}\)

两条平行直线之间距离：\(\displaystyle \boxed{d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}}\)

若 \(y=kx+b\)，则直线上两点间距离 \(|AB|=\sqrt{1+k^2}|x_1-x_2|=\sqrt{1+\frac{1}{k^2}}|y_1-y_2|\)

对称问题

1. 点 \((x,y)\) 关于 \((a,b)\) 对称点为 \((2a-x,2b-y)\)。
2. 直线 \(l:Ax+By+C=0\) 关于点 \((x_0,y_0)\) 的对称直线 \(A(2x_0-x)+B(2y_0-y)+C=0\)。
3. 点关于直线的对称点通过设中点来列方程求。

圆

圆的标准方程：\((x-a)^2+(y-b)^2=r^2\)

圆的一般方程：\(x^2+y^2+Dx+Ey+F=0\)，其中 \(D^2+E^2-4F>0\)，化为标准形式为 \(\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle\boxed{\left(x+\frac{D}{2}\right)^2+\left(y+\frac{E}{2}\right)^2=\frac{D^2+E^2-4F}{4}}\)

两圆关系	内含	内切	相交	外切	相离
公切线数	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)

以 \((x_1,y_1),(x_2,y_2)\) 为直径的两端点的圆的方程：

\[(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0 \]

过圆 \((x-a)^2+(y-b)^2=r^2\) 上一点 \((x_0,y_0)\) 的切线方程为

\[(x-a)(x_0-a)+(y-b)(y_0-b)=r^2 \]

过圆 \(x^2+y^2+Dx+Ey+F=0\ (D^2+E^2-4F>0)\) 上一点 \((x_0,y_0)\) 的切线方程为

\[x_0x+y_0y+\frac{D(x+x_0)}{2}+\frac{E(y+y_0)}{2}+F=0 \]

设点 \(M(x_0,y_0)\) 是圆 \((x-a)^2+(y-b)^2=r^2\) 外一点，过点 \(M\) 作圆的两条切线，切点分别为 \(A,B\)，则直线 \(AB\) 的方程为

\[(x-a)(x_0-a)+(y-b)(y_0-b)=r^2 \]

经过圆外一点 \(P(x_0,y_0)\) 引圆的两条切线，则

圆的方程	切线长公式
\((x-a)^2+(y-b)^2=r^2\)	\(\sqrt{(x_0-a)^2+(y_0-b)^2-r^2}\)
\(x^2+y^2+Dx+Ey+F=0 \\ (D^2+E^2-4F>0)\)	\(\sqrt{x_0^2+y_0^2+Dx_0+Ey_0+F}\)

两圆相交时，两圆方程做差得到公共弦所在直线的方程，即

\[D_1x+E_1y+F_1-(D_2x+E_2y+F_2)=0 \]

参数方程：\(P(x,y)\) 满足 \(\begin{cases}x=a+r\cos\theta \\ y=b+r\sin\theta\end{cases}(r>0)\) 的轨迹为 \((x-a)^2+(y-b)^2=r^2\)。

圆锥曲线的方程

椭圆

• 概念：平面内到两个焦点 \(F_1,F_2\) 的距离的和等于常数（ 大于 \(|F_1F_2|\) ）的点的轨迹叫做椭圆。

集合 \(P=\set{M||MF_1|+|MF_2|=2a},|F_1F_2|=2c\)

标准方程	\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\\\) 焦点在 \(x\) 轴上	\(\frac{x^2}{b^2}+\frac{y^2}{a^2}=1(a>b>0)\\\) 焦点在 \(y\) 轴上
顶点坐标	\((\pm a,0),(0,\pm b)\)	\((\pm b,0),(0,\pm a)\)
对称轴	\(x\) 轴、\(y\) 轴	\(x\) 轴、\(y\) 轴
焦点坐标	\((\pm c,0)\)	\((0,\pm c)\)
准线	\(x=\pm\frac{a^2}{c}\)

• \(\boxed{c^2=a^2-b^2}\)，离心率 \(\boxed{e=\frac{c}{a}}\ (0<e<1)\)

\(e\) 越趋近于 \(1\) ，椭圆越扁；否则越圆。

椭圆的面积：\(S=\pi ab\)（ \(a,b\) 分别为长半轴、短半轴的长 ）。

准线：椭圆上一点 \(M(x,y)\) 与顶点 \(F(\pm c,0)\) 的距离和它到定直线 \(l:x=\pm\frac{a^2}{c}\) 的距离比是常数 \(e\)（ 椭圆的第二定义 ）。

椭圆的第三定义：设 \(A(-a,0),B(a,0),P(x,y)\in C\)，则 \(\boxed{k_{AP}\cdot k_{BP}=-\frac{b^2}{a^2}=e^2-1}\)。

椭圆焦点三角形的性质

椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 上异于左、右顶点的点 \(P(x_0,y_0)\) 与两焦点 \(F_1,F_2\) 构成的 \(\Delta PF_1F_2\) 叫做焦点三角形。

以下记 \(\angle F_1PF_2=\theta\)。

1. 周长 \(C=2(a+c)\)。

2. 面积 \(\boxed{S=b^2\tan\frac{\theta}{2}=c|y_0|=\frac{1}{2}|PF_1||PF_2|\sin\theta=r(a+c)}\)，\(r\) 为焦点三角形的内接圆半径，当 \(y_0=b\) 即点 \(P\) 的位置为短轴端点时取最大值，且 \(\cos\theta\geq 1-2e^2\)。

   证明：由余弦定理，

   \[|F_1F_2|^2=|PF_1|^2+|PF_2|^2-2|PF_1||PF_2|\cos\theta=(|PF_1|+|PF_2|)^2-2(1+\cos\theta)\cdot|PF_1||PF_2| \]

   因为 \(|PF_1|+|PF_2|=2a,|F_1F_2|=2c\)，所以 \(|PF_1||PF_2|=\frac{2a^2-2c^2}{1+\cos\theta}=\frac{2b^2}{1+\cos\theta}\)

   又因为 \(\frac{\sin\theta}{1+\cos\theta}=\frac{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}{1+(2\cos^2\frac{\theta}{2}-1)}=\frac{\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}}=\tan\frac{\theta}{2}\)

   因此 \(S=\frac{1}{2}|PF_1||PF_2|\sin\theta=\frac{b^2\sin\theta}{1+\cos\theta}=b^2\tan\frac{\theta}{2}\)

3. \(|PF_1|\cdot|PF_2|\in (b^2,a^2]\)

4. 设 \(\angle PF_1F_2=\alpha,PF_2F_1=\beta\)，则 \(\displaystyle\boxed{e=\frac{\sin(\alpha+\beta)}{\sin\alpha+\sin\beta}}=\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha-\beta}{2}}\) （ 证明：正弦定理 ）。

5. 若焦点三角形内切圆的圆心为 \(I\)，延长 \(PI\) 交 \(F_1F_2\) 于点 \(Q\)，则

   \[\frac{|PI|}{|IQ|}=\frac{|PF_1|}{|F_1Q|}=\frac{|PF_2|}{|F_2Q|}=\frac{|PF_1|+|PF_2|}{|F_1Q|+|F_2Q|}=\frac{2a}{2c}=\frac{1}{e} \]

6. 若椭圆上存在点 \(P\) 使得 \(\angle F_1PF_2=\theta\)，则 \(e\in[\sin\frac{\theta}{2},1)\)。

椭圆的其它几何性质

• 通径：过椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 的焦点作垂直于长轴的直线，该直线被椭圆截得的弦叫做通径，其长度为 \(\frac{2b^2}{a}\)。

  若不垂直，则其长度为 \(|PP_0|=\frac{\frac{2b^2}{a}}{1-e^2\cos^2\theta}\geq \frac{2b^2}{a}\)

• 焦半径：设 \(P(x,y)\in C,F_1(-c,0),F_2(c,0)\)，则 \(|PF_1|=\sqrt{(x+c)^2+b^2\frac{a^2-x^2}{a^2}}=\sqrt{\frac{c^2}{a^2}x^2+2cx+a^2}=|a+ex|\)，同理 \(|PF_2|=a-ex\)，因此 \(\boxed{|PF|=|a\pm ex|}\)。

• 焦点弦（ 过焦点的弦 ）：设 \(AB\) 是过椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\ (a>b>0)\) 的右焦点 \(F\)的一条弦，\(A(x_1,y_1),B(x_2,y_2),AB\) 的倾斜角为 \(\theta\)，准线 \(l:x=\frac{a^2}{c}\)，则 \(\boxed{\frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta},|AB|=\frac{2a(1-e^2)}{1-e^2\cos^2\theta}}\)。

  证明：过 \(A\) 作 \(AA_1\perp AB\) 于点 \(A_1\)，则 \(|AF|=e|AA_1|=e(\frac{a^2}{c}-c-|AF|\cos\theta)\implies|AF|=\frac{b^2}{a+c\cos\theta}\)

  同理 \(|BF|=\frac{b^2}{a-c\cos\theta}\)，代入得证。

  注：一条过焦点的直线会有两个一长一短的焦半径，在公式中，长的对应取减号，短的对应取加号；当焦点在 \(y\) 轴上，将 \(\cos\theta\) 换为 \(\sin\theta\)。

• 过一个焦点 \(F\) 作弦 \(AB,AF=d_1,BF=d_2\)，则 \(\displaystyle\frac{1}{d_1}+\frac{1}{d_2}=\frac{2a}{b^2}\)

• 弦长公式：设直线 \(y=kx+m\) 与椭圆有两个公共点 \(M(x_1,y_1),N(x_2y_2)\)，则弦长公式：

\[|MN|=\sqrt{(1+k^2)[(x_1+x_2)^2-4x_1x_2]}=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]} \]

• 中点弦问题：求直线 \(AB\) 与圆锥曲线相交弦的中点 \(M\) 和原点的连线 \(OM\) 的斜率问题，\(\\\) 有 \(\boxed{k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2}=e^2-1}\) （ 若焦点在 \(y\) 轴，则 \(k_{AB}\cdot k_{OM}=-\frac{a^2}{b^2}\) ）

  证明：联立 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\ (a>b>0)\) 与 \(y=k_{AB}x+m\) 得

  \[(b^2+a^2k_{AB}^2)x^2+2mk_{AB}a^2x+a^2m^2-a^2b^2=0 \]

  所以 \(x_1+x_2=\frac{-2mk_{AB}a^2}{b^2+a^2k_{AB}^2},M_x=\frac{x_1+x_2}{2}=\frac{-mk_{AB}a^2}{b^2+a^2k_{AB}^2},m=\frac{b^2+a^2k_{AB}^2}{-k_{AB}a^2}M_x\)

  代入 \(y=k_{AB}x+m\) 得 \(y=-\frac{b^2}{k_{AB}a^2}x\implies k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2}\)

  例题：过椭圆 \(\frac{x^2}{16}+\frac{y^2}{4}=1\) 内一点 \(P(3,1)\)，且被这点平分的弦所在的直线方程是 ？

  方法一：设 \(A(x_1,y_1),B(x_2,y_2)\implies \frac{x_1^2}{16}+\frac{y_1^2}{4}=1,\frac{x_2^2}{16}+\frac{y_2^2}{4}=1\)，两式相减得 \(\frac{(x_1+x_2)(x_1-x_2)}{16}+\frac{(y_1+y_2)(y_1-y_2)}{4}=0\)

  \(P\) 为 \(AB\) 中点 \(\implies x_1+x_2=6,y_1+y_2=2 \implies k_{AB}=\frac{y_1-y_2}{x_1-x_2}=-\frac{3}{4}\)

  所以直线 \(AB\) 的方程是 \(3x+4y-13=0\)。

  方法二：设弦为 \(AB,k_{OP}=\frac{1}{3},k_{AB}=-\frac{b^2}{a^2}\div\frac{1}{3}=-\frac{3}{4}\)，后同方法一。

• 中点弦问题的推广：椭圆上的点 \(P\) 与过椭圆中心的弦 \(AB\) 的端点的连线 \(MA,MB\) 斜率之积为 \(\boxed{-\frac{b^2}{a^2}=e^2-1}\)

  证明：作中位线 \(OT\)，易证 \(k_{MA}\cdot k_{MB}=k_{MA}\cdot k_{OT}=-\frac{b^2}{a^2}=e^2-1\)

• 蒙日圆：椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆上，且圆的方程为 \(x^2+y^2=a^2+b^2\)。

  过蒙日圆上一点 \(M\) 做关于椭圆的切线，与椭圆交于 \(A,B\)，\(D\) 为椭圆上任意一点，则 \(\boxed{k_{DA}k_{DB}=e^2-1}\)。

• 椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 在 \((x_0,y_0)\) 处的切线方程为 \(\frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1\)，直接设直线 \(y=kx+m\)，算 \(\Delta\) 得证。

• 过椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 上任意一点 \(P\)（ 不是椭圆的顶点 ）作椭圆的切线，设切线的斜率为 \(k_1\)，直线 \(OP\) 的斜率为 \(k_2\)，则 \(\boxed{k_1k_2=e^2-1}\)，双曲线同样成立。

• 过原点 \(O\) 的直线 \(l\) 与椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 相交于 \(A,B\) 两点，\(P\) 为椭圆上任意一点，则 \(k_{PA}k_{PB}=e^2-1\)。

• 过椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 上的任意一点 \(P\)（ 非顶点 ）作倾斜角互补的两条直线交椭圆于 \(A,B\) 两点，有 \(k_{AB}k_{OP}=1-e^2\)。

如果是焦点在 \(y\) 轴上的椭圆或双曲线，则 \(\boxed{e^2-1\to\frac{1}{e^2-1}}\)。

• \(A,B\) 是椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 上任意两点，\(S_{\Delta AOB\max}=\frac{1}{2}ab\)。

• \(A,B\) 是椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 上任意两点，并且 \(OA\perp OB\implies \frac{1}{|OA|^2}+\frac{1}{|OB|^2}=\frac{1}{a^2}+\frac{1}{b^2}\)。

• 椭圆两焦点到椭圆上任意一条切线的距离之积为定值 \(b^2\)。
  证明：设切点为 \((x_0,y_0)\)，切线方程为 \(b^2x_0x+a^2y_0y=a^2b^2\)，距离 \(d_1=\frac{|-b^2x_0c-a^2b^2|}{\sqrt{b^4x_0^2+a^4y_0^2}},d_2=\frac{|b^2x_0c-a^2b^2|}{\sqrt{b^4x_0^2+a^4y_0^2}}\)，则

  \[d_1d_2=\frac{|a^4b^4-b^4x_0^2c^2|}{b^4x_0^2+a^4y_0^2}\xlongequal{b^2x_0^2+a^2y_0^2=a^2b^2}b^2\frac{a^4b^2-a^2b^2x_0^2+b^4x_0^2}{b^4x_0^2+a^4b^2-a^2b^2x_0^2}=b^2 \]

好题

1. 设直线 \(l:y=x+1\) 与椭圆 \(C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 相交于 \(A,B\) 两点，与 \(x\) 轴相交于左焦点 \(F\)，且 \(\overrightarrow{AF}=3\overrightarrow{FB}\)，则椭圆的离心率 \(e=\) _______

答案：\(\frac{\sqrt{2}}{2}\)

解析：方法一：由题得 \(F(-1,0),c=1\)，设 \(A(x_1,y_1),B(x_2,y_2)\)，联立 \(y=x+1\) 与椭圆方程 \(b^2x^2+a^2y^2=a^2b^2\) 得

\((a^2+b^2)y^2-2b^2y+b^2-a^2b^2=0\)，显然 \(\Delta>0,y_1+y_2=\frac{2b^2}{a^2+b^2},y_1y_2=\frac{b^2-a^2b^2}{a^2+b^2}\ \circledast\)

由 \(\overrightarrow{AF}=3\overrightarrow{FB}\) 得 \(0-y_1=3(y_2-0)\) 即 \(y_1=-3y_2\ \circledcirc\)

由 \(\circledast \circledcirc\) 消去 \(y_1,y_2\) 得 \(-3b^2=(a^2+b^2)(1-a^2)\xRightarrow{a^2-b^2=c^2=1}a^4-3a^2+1=0\implies a=\pm\sqrt{2}\ \text{or}\ \pm 1\)

取 \(a=\sqrt{2}\)，所以 \(e=\frac{c}{a}=\frac{\sqrt{2}}{2}\)。

方法二：注意上述关于焦点弦的结论，\(\frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta}=3\)，代入 \(\cos\theta=\frac{\sqrt{2}}{2}\) 可得 \(e=\frac{\sqrt{2}}{2}\)

---

2. 已知椭圆 \(\frac{x^2}{4}+y^2=1\)，直线 \(l:y=kx+m\) 满足 \(m\neq -2k\) 且与椭圆相交于不同的两点 \(A,B\)，若以线段 \(AB\) 为直径的圆始终过点 \(Q(2,0)\)，试判断直线 \(l\) 是否过定点？若是，求出该定点的坐标；若不是，请说明理由。

解：设 \(A(x_1,y_1),B(x_2,y_2)\)，联立 \(\begin{cases} y=kx+m \\ \frac{x^2}{4}+y^2=1 \end{cases}\)

得 \((1+4k^2)x^2+8kmx+4m^2-4=0,\Delta=16(4k^2-m+1)>0\)

则 \(x_1+x_2=\frac{-8km}{1+4k^2},x_1x_2=\frac{4m^2-4}{1+4k^2},y_1y_2=(kx_1+m)(kx_2+m)=k^2x_1x_2+km(x_1+x_2)+m^2=\frac{m^2-4k^2}{1+4k^2}\)

因为以线段 \(AB\) 为直径的圆过点 \(Q\)，所以 \(\overrightarrow{QB}\cdot\overrightarrow{QA}=0\)，又 \(\overrightarrow{QB}=(x_2-2,y_2),\overrightarrow{QA}=(x_1-2,y_1)\)

所以 \(\overrightarrow{QB}\cdot\overrightarrow{QA}=x_1x_2-2(x_1+x_2)+4+y_1y_2=\frac{(6k+5m)(2k+m)}{1+4k^2}=0\)

显然 \(m=-\frac{6}{5}k\implies l:y=kx-\frac{6}{5}k=k(x-\frac{6}{5})\)，恒过定点 \((\frac{6}{5},0)\)。

---

（ 齐次化 ）3. 已知 \(\frac{x^2}{4}+\frac{y^2}{3}=1\)，是否存在定圆与 \(MN(OM\perp ON)\)（ 动直线 ）总相切 ？

设 \(MN:mx+ny=1\)，代入得 \(3x^2+4y^2-12(mx+ny)^2=0\implies (3-12m^2)x^2+(4-12n^2)y^2-24mnxy=0\)

化成 \((4-12n^2)k^2-24mnk+3-12m^2=0\)，因为 \(k_1k_2=\frac{3-12m^2}{4-12n^2}=-1\)，因此 \(m^2+n^2=\frac{7}{12}\)，定圆为 \(x^2+y^2=\frac{12}{7}\)。

---

（ 定比点差法 ）4. 已知 \(\frac{x^2}{4}+y^2=1,A(-2,0)\)，经过 \(B(1,0)\) 且斜率存在的直线 \(l\) 交椭圆于 \(P,Q\) 两点，点 \(C\) 与点 \(P\) 关于坐标原点对称，连接 \(AC,AQ\)，求 \(\frac{k_{AC}}{k_{AQ}}\) 的值。

设 \(P(x_1,y_1),Q(x_2,y_2),\overrightarrow{PB}=\lambda\overrightarrow{BQ}\)，则 \(x_1+\lambda x_2=1+\lambda,y_1+\lambda y_2=0\)

\(\begin{cases} \frac{x_1^2}{4}+y_1^2=1 \\ \frac{x_2^2}{4}+y_2^2=1 \end{cases}\implies \begin{cases} \frac{x_1^2}{4}+y_1^2=1 \\ \frac{\lambda x_2^2}{4}+\lambda y_2^2=\lambda \end{cases}\)

两式作差得 \(\frac{(x_1+\lambda x_2)(x_1-\lambda x_2)}{4}+(y_1+\lambda y_2)(y_1-\lambda y_2)=1-\lambda ^2\)

代入解得 \(x_1=\frac{5-3\lambda}{2},x_2=\frac{5\lambda -3}{2\lambda},\frac{k_{AC}}{k_{AQ}}=\frac{y_1(x_2+2)}{y_2(x_1-2)}=\frac{-\lambda(x_2+2)}{x_1-2}=\frac{3-9\lambda}{1-3\lambda}=3\)

• 练习题：设 \(F_1,F_2\) 分别是椭圆 \(\frac{x^2}{3}+y^2=1\) 的左右焦点，点 \(A,B\) 在椭圆上，\(\overrightarrow{F_1A}=5\overrightarrow{F_2B}\)，则点 \(A\) 的坐标是 ？（ 答案：\((0,\pm 1)\) ）

---

（ 正难则反 ）5. 设椭圆 \(\frac{x^2}{a^2}+y^2=1(a>1)\)，若以点 \(A(0,1)\) 为圆心的圆与椭圆至多有 \(3\) 个公共点，求 \(e\) 范围？

从反面考虑，若有 \(4\) 个公共点，可知在 \(y\) 轴两侧各有 \(2\) 个交点，可知椭圆的一侧存在一个等腰 \(\Delta APQ,AP=AQ\)。

设 \(PQ\) 中点为 \(M(x_0,y_0)\)，则 \(k_{OM}k_{PQ}=e^2-1=-\frac{1}{a^2}\)。因为 \(k_{AM}k_{PQ}=\frac{y_0-1}{x_0}k_{PQ}=-1\)，

两式相除得 \(\frac{y_0-1}{y_0}=a^2>2\)，得出 \(e\in(0,\frac{\sqrt{2}}{2}]\)。

---

（ 齐次化 ）6. （ 2022 I 卷，T22 ）已知 \(C:\frac{x^2}{6}+\frac{y^2}{3}=1,A(2,1)\)，点 \(M,N\) 在 \(C\) 上，\(AM\perp AN,AD\perp MN\)，\(D\) 为垂足，证明：存在定点 \(Q\)，使得 \(|DQ|\) 是定值。

方法一：设 \(MN:y=kx+m\)，暴力联立 \(+\) 向量得 \((2k+3m+1)(2k+m-1)=0\)，得出 \(MN\) 过定点 \(P(\frac{2}{3},-\frac{1}{3})\)。令 \(Q(\frac{4}{3},\frac{1}{3})\) 为 \(AP\) 中点，得出 \(|DQ|=\frac{1}{2}|AP|=\frac{2\sqrt{2}}{3}\) 是定值。

方法二：先将 \(C\) 平移一下，变为 \(\frac{(x+2)^2}{6}+\frac{(y+1)^2}{3}=1\)，使得 \(A\) 点在新坐标的原点上。设 \(MN:mx+ny=1\)，联立得 \((2+4n)(\frac{y}{x})^2+4(m+n)\frac{y}{x}+4m+1=0\)，显然 \(\frac{y_1y_2}{x_1x_2}=\frac{4m+1}{2+4n}=-1\)，得到 \((-\frac{4}{3})m+(-\frac{4}{3})n=1\)，即定点 \((\frac{2}{3},-\frac{1}{3})\)。

---

（ 点差法 + 二次代换消元 ）7. （ 华附 2024 5 月测试 ）已知 \(E:\frac{x^2}{4}+y^2=1\)，\(E\) 上有 \(3\) 点 \(G,S,T\)，直线 \(ST\) 过点 \(C(2,2)\)，点 \(M\) 为 \(GS\) 中点且在直线 \(y=x\) 上，证明：直线 \(GT\) 与直线 \(y=x\) 的交点为定点。

设 \(S(x_1,y_1),T(x_2,y_2),G(x_3,y_3)\)，进行一次点差法：\(\frac{x_1^2}{4}+y_1^2=1,\frac{x_3^2}{4}+y_3^2=1\)，相减得 \(\frac{y_1-y_3}{x_1-x_3}=-\frac{y_1+y_3}{4(x_1+x_3)}\)

因为 \(GT\) 中点在 \(y=x\) 上所以 \(y_1+y_3=x_1+x_3\) 得 \(y_1-y_3=-\frac{1}{4}(x_1-x_3)\)。

两式相加得 \(2y_1=\frac{3}{4}x_1+\frac{5}{4}x_3\implies x_3=\frac{8y_1-3x_1}{5},y_3=\frac{3y_1+2x_1}{5}\)

代入 \(GT:\frac{y-y_3}{x-x_3}=\frac{y-y_2}{x-x_2}\) 得 \((5y_2-3y_1-2x_1)x+(8y_1-3x_1-5x_2)y=-3(x_1y_2+x_2y_1)+8y_1y_2-2x_1x_2\)

设交点为 \((m,m)\)，代入得 \(5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)\)

即证明存在 \(m\) 使该式恒成立。

由直线 \(ST\) 过点 \(C(2,2),\frac{y_2-2}{x_2-2}=\frac{y_1-2}{x_1-2}\implies x_1(y_2-2)-x_2(y_1-2)=2(y_2-y_1)\)，进行二次代换凑出和积：

\[x_1(y_2-2)+x_2(y_1-2)=\frac{x_1^2(y_2-2)^2-x_2^2(y_1-2)^2}{x_1(y_2-2)-x_2(y_1-2)}=\frac{(4-4y_1^2)(y_2-2)^2-(4-4y_2^2)(y_1-2)^2}{2(y_2-y_1)}=10(y_1+y_2)-8-8y_1y_2 \]

即 \(x_1y_2+x_2y_1=2(x_1+x_2)+10(y_1+y_2)-8-8y_1y_2\) ①

同理有 \((x_1-2)y_2-(x_2-2)y_1=-2(x_2-x_1)\)

\[(x_1-2)y_2-(x_2-2)y_1=\frac{(x_1-2)^2y_2^2-(x_2-2)^2y_1^2}{(x_1-2)y_2-(x_2-2)y_1}=\frac{(x_1-2)^2(1-\frac{x_2^2}{4})-(x_2-2)^2(1-\frac{x_1^2}{4})}{-2(x_2-x_1)} \]

即 \(x_1y_2+x_2y_1=(x_1+x_2)+2(y_1+y_2)-2-\frac{1}{2}x_1x_2\) ②

两式比对系数凑配出 \(8y_1y_2-2x_1x_2\) 和目标式比对：

\(4\times\) ② \(-\) ① 得 \(2(y_1+y_2)-2(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)\)

对比 \(5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)\) 得 \(m=\frac{2}{5}\) 时恒成立。

故定点为 \((\frac{2}{5},\frac{2}{5})\)。

双曲线

• 概念：平面内到两个焦点 \(F_1,F_2\) 的距离的差等于非零常数（ 小于 \(|F_1F_2|\) ）的点的轨迹叫做双曲线。

双曲线就是下列点的集合 \(P=\set{M|||MF_1|-|MF_2||=2a}\)，\(|F_1F_2|=2c>2a\)。

标准方程	\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\\\) 焦点在 \(x\) 轴上	\(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0)\) 焦点在 \(y\) 轴上
顶点坐标	\((\pm a,0)\)	\((0,\pm a)\)
焦点坐标	\((\pm c,0)\)	\((0,\pm c)\)
渐近线方程	\(y=\pm\frac{b}{a}x\)	\(y=\pm\frac{a}{b}x\)

• \(\boxed{c^2=a^2+b^2}\)，离心率 \(\boxed{e=\frac{c}{a}}\ (e>1)\)

实轴长 \(=2a\) 虚轴长 \(=2b\)。

等轴双曲线：\(a=b\) 的双曲线。

\(e\) 越大，双曲线开口越大。

一般方程：\(Ax^2+By^2=1(AB<0)\)。

双曲线与它的渐近线无限接近但永不相交，求渐近线方程时，只要令 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=0\) 即可。

第二定义：平面内动点 \(M\) 到定点 \(F\) 的距离和它到准线 \(l:x=\pm\frac{a^2}{c}\) 的距离之比等于 \(e\)。

• 与两定点 \(A_1(-a,0),A_2(a,0)(a\neq 0)\) 连线的斜率之积为 \(\frac{b^2}{a^2}=e^2-1\) 的点的轨迹为双曲线。

双曲线焦点三角形的性质

双曲线 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)\) 上异于顶点的点 \(P(x_0,y_0)\) 与两焦点构成的 \(\Delta PF_1F_2\) 叫做焦点三角形。

以下记 \(\angle F_1PF_2=\theta\)。

1. 面积 \(\boxed{S=\frac{b^2}{\tan\frac{\theta}{2}}=c|y_0|}\)。

2. 设 \(\angle PF_1F_2=\alpha,\angle PF_2F_1=\beta,P\) 为双曲线右支上一点，则 \(\frac{|PF_1|}{\sin\beta}=\frac{|PF_2|}{\sin\alpha}=\frac{|PF_1|-|PF_2|}{\sin\beta-\sin\alpha}=\frac{2a}{\sin\beta-\sin\alpha}=\frac{|F_1F_2|}{\sin(\alpha+\beta)}=\frac{2c}{\sin\theta}\)，所以 \(\boxed{e=\frac{\sin(\alpha+\beta)}{\sin\beta-\sin\alpha}}\)。

3. 若焦点三角形内切圆的圆心为 \(I(x_1,y_1)\)，与三边的切点分别为 \(M,N,R\)，则 \(|F_1R|-|F_2R|=|F_1M|-|F_2N|=|PF_1|-|PF_2|=2a\)，即 \(c+x_1-(c-x_1)=2a\)，解得 \(x_1=a\)。

4. 过双曲线焦点 \((c,0)\) 作渐近线 \(y=\frac{b}{a}x\) 的垂线，垂足长度为 \(b\)，形成的三角形满足 \(a^2+b^2=c^2\)。

双曲线的其它几何性质

• 通径：过双曲线 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)\) 的焦点作垂直于实轴所在的直线，该直线被双曲线截得的弦叫做通径，长度为 \(\frac{2b^2}{a}\)。

• 弦长公式：设直线 \(y=kx+m\) 与双曲线有两个公共点 \(M(x_1,y_1),N(x_2,y_2)\)，则 \(|MN|=\sqrt{(1+k^2)[(x_1+x_2)^2-4x_1x_2]}=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]}\)

• 焦半径：双曲线一点 \(P(x_0,y_0)\) 与左（ 下 ）焦点 \(F_1\)或右（ 上 ）焦点 \(F_2\) 之间的线段叫做双曲线的焦半径，分别记作 \(r_1=|PF_1|,r_2=|PF_2|\)。

  1. \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)\)，若点 \(P\) 在双曲线右支上，则 \(r_1=ex_0+a,r_2=ex_0-a\)；若点 \(P\) 在双曲线左支上，则 \(r_1=-ex_0-a,r_2=-ex_0+a\)。
  2. \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\ (a>0,b>0)\)，若点 \(P\) 在双曲线上支上，则 \(r_1=ey_0+a,r_2=ey_0-a\)；若点 \(P\) 在双曲线下支上，则 \(r_1=-ey_0-a,r_2=-ey_0+a\)。

• 设 \(AB\) 是 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\) 的一条弦，\(AB\) 中点为 \(M(x_0,y_0)\)，则 \(k_{AB}=\frac{b^2x_0}{a^2y_0}\)，\(\boxed{k_{AB}k_{OM}=e^2-1}\)。

• 已知双曲线 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\)，过双曲线的左焦点 \(F(-c,0)\) 的直线交双曲线于 \(A,B\) 两点，交 \(y\) 轴于点 \(P\)，设 \(\overrightarrow{PF}=\lambda_1\overrightarrow{FA}=\lambda_2\overrightarrow{FB}\)，则 \(\lambda_1+\lambda_2=\frac{2e^2}{1-e^2}\)
  扩展：若 \(F\) 改为 \(x\) 轴上一点 \(M(m,0)\)，则 \(\lambda_1+\lambda_2=\frac{2m^2}{a^2-m^2}\)。

• 对于双曲线上一点 \(P\) 做切线交两条渐近线于 \(A,B\)，则 \(S_{\Delta PAB}=ab\)
  证明：\(OA:\frac{x}{a^2}-\frac{y}{b^2}=0,OB:\frac{x}{a^2}+\frac{y}{b^2}=0,AB:\frac{x_0x}{a^2}-\frac{y_0y}{b^2}=1\)

  设 \(A(x_1,y_1),B(x_2,y_2),P(x_0,y_0)\)，分别代入得 \(\frac{x_0x_1}{a^2}-\frac{y_0y_1}{b^2}=1,\frac{x_0x_2}{a^2}-\frac{y_0y_2}{b^2}=1\)

  代入 \(y_1=\frac{b}{a}x_1,y_2=-\frac{b}{a}x_2\) 得到 \(\begin{cases}\frac{x_1}{a}(\frac{x_0}{a}-\frac{y_0}{b})=1 \\ \frac{x_2}{a}(\frac{x_0}{a}+\frac{y_0}{b})\end{cases}\)

  相乘：\(\frac{x_1^2x_2^2}{a^2}(\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2})=1\implies x_1x_2=a^2,OA\cdot OB=\frac{a^2+b^2}{a^2}x_1x_2=a^2+b^2=c^2\)

  \(\sin\angle AOB=\sin 2\angle AOx=2\sin\angle AOx\cos\angle AOx=2\frac{ab}{c^2} \\ S=\frac{1}{2}OA\cdot OB\sin\angle AOB=ab\)

好题

1. 若双曲线的一条渐近线过点 \((8,-6)\)，则其离心率等于 ？

分 \(2\) 种情况讨论，焦点在 \(x\) 轴上（ \(\frac{b}{a}=\frac{3}{4}\ \ \ e=\frac{5}{4}\) ），在 \(y\) 轴上（ \(\frac{a}{b}=\frac{3}{4}\ \ \ e=\frac{5}{3}\) ）

---

2. 动圆 \(M\) 与圆 \(C_1:(x+4)^2+y^2=1\)，圆 \(C_2:(x-4)^2+y^2=9\) 都外切，则动圆圆心 \(M\) 的轨迹方程为 ？

解：圆 \(C_1(-4,0),r_1=1,C_2(4,0),r_2=3\)，设 \(M(x,y)\)，半径为 \(r\)，则 \(\begin{cases} |MC_1|=r+1 \\ |MC_2|=r+3 \end{cases}\)

即 \(|MC_2|-|MC_1|=2<|C_1C_2|\)，所以 \(M\) 的轨迹为以 \(C_1,C_2\) 为焦点，\(2a=2\) 的双曲线的左支，\(b=\sqrt{15}\)。

所以 \(M\) 的轨迹方程为 \(x^2-\frac{y^2}{15}=1\ (x\leq -1)\)。

---

3. 是否存在过点 \(P(1,-\frac{1}{2})\) 的直线 \(l\) 与双曲线 \(\frac{x^2}{2}-y^2=1\) 相交于 \(A,B\) 两点，且满足 \(P\) 是线段 \(AB\) 的中点？若存在，求出直线 \(l\) 的方程；若不存在，请说明理由。

（ 点差法 ）解：设 \(l:y=k(x-1)-\frac{1}{2},A(x_1,y_1),B(x_2,y_2)\)，则 \(\begin{cases} \frac{x_1^2}{2}-y_1^2=1 \\ \frac{x_2^2}{2}-y_2^2=1 \end{cases}\)，

两式相减得 \((x_1-x_2)(x_1+x_2)=2(y_1-y_2)(y_1+y_2)\)，因为 \(P(1,-\frac{1}{2})\) 为线段 \(AB\) 的中点，则

\[x_1+x_2=2,y_1+y_2=-1,k=\frac{y_1-y_2}{x_1-x_2}=\frac{x_1+x_2}{2(y_1+y_2)}=-1\implies l:y=-x+\frac{1}{2} \]

联立 \(\begin{cases} y=-x+\frac{1}{2} \\ \frac{x^2}{2}-y^2=1 \end{cases}\) 消去 \(y\) 可得 \(2x^2-4x+5=0,\Delta<0\)，方程无实根，故 \(l\) 不存在。

---

4. [ 安徽十校联盟 2023 期中 ] 已知双曲线 \(C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)\) 的左、右焦点分别为 \(F_1,F_2\)，焦距为 \(4\)，点 \(M\) 在圆 \(E:x^2+y^2+4x-8y+16=0\) 上，且 \(C\) 的一条渐近线上存在点 \(N\)，使得四边形 \(OMNF_2\) 为平行四边形，\(O\) 为坐标原点，则 \(C\) 的离心率的取值范围为（ ）

   \(\text{A.} [2,+\infty)\ \ \ \ \ \ \text{B.} [\sqrt{3},+\infty)\ \ \ \ \ \ \text{C.} [4,+\infty)\ \ \ \ \ \ \text{D.} (1,\sqrt{3})\)

   答案：\(\text{A}\)。

---

5. 已知直线 \(y=ax+1\) 与双曲线 \(3x^2-y^2=1\) 交于 \(A,B\) 两点。

   \((1)\) 若以 \(AB\) 为直径的圆过坐标原点 \(O\)，求实数 \(a\) 的值。

   \((2)\) 是否存在这样的实数 \(a\)，使 \(A,B\) 两点关于直线 \(y=\frac{1}{2}x\) 对称？若存在，请求出 \(a\) 的值；若不存在，请说明理由。

解：\((1)\) 联立 \(\begin{cases} y=ax+1\\ 3x^2-y^2=1 \end{cases}\) 消去 \(y\) 得 \((3-a^2)x^2-2ax-2=0\)，依题意 \(\begin{cases} 3-a^2\neq 0\\ \Delta >0 \end{cases}\\\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \text{}\)解得 \(-\sqrt{6}<a<\sqrt{6}\) 且 \(a\neq\pm\sqrt{3}\)，设 \(A(x_1,y_1),B(x_2,y_2)\)，则 \(\begin{cases} x_1+x_2=\frac{2a}{3-a^2} \\ x_1x_2=\frac{-2}{3-a^2} \end{cases}\)

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \because\) 以 \(AB\) 为直径的圆过坐标原点 \(O\ \ \ \therefore OA\perp OB,\ \overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=0\ \ \ \ \ \ \because y_1y_2=a^2x_1x_2+a(x_1+x_2)+1\)

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \therefore x_1x_2+y_1y_2=(a^2+1)x_1x_2+a(x_1+x_2)+1=(a^2+1)\cdot\frac{-2}{3-a^2}+\frac{2a^2}{3-a^2}+1=0\implies a=\pm 1\)

\(\ \ \ \ \ \ \ (2)\) 假设存在实数 \(a\)，使 \(A,B\) 两点关于直线 \(y=\frac{1}{2}x\) 对称，则 \(a=-2\) 检验后可排除，故 \(a\) 不存在。

---

（ 齐次化 ）6. 已知 \(C:x^2+y^2=4\)，\(A(-2,0),B(2,0)\)，\(P\) 在 \(x=4\) 上，\(PA,PB\) 与 \(C\) 交于 \(M(x_1,y_1),N(x_2,y_2)\)，求直线 \(MN\) 的定点？

解：设 \(P(4,t)\implies 3k_{PA}=k_{PB},MN:my=x+t\)，因此 \(\frac{y_2}{x_2-2}=\frac{3y_1}{x_1+2}\implies\frac{y_2}{my_2-(t+2)}=\frac{3y_1}{my_1+(2-t)}\implies 2my_1y_2=(3t+6)(y_1+y_2)-(4t+4)y_2\implies \frac{-4m(t+1)(t+2)}{m^2+1}=-4(t+1)y_2\)

所以 \(k_{PB}k_{BM}=-3\)，再设 \(y=kx+3\dots\)

---

7. 设 \(F_1,F_2\) 为双曲线 \(C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\) 的左右焦点，\(A\) 是右支上一点，\(\Delta AF_1F_2\) 内切圆圆心为 \(M\)，半径为 \(a\)，\(\exist \lambda\in\R,\overrightarrow{AM}+2\overrightarrow{OM}=\lambda\overrightarrow{OF_2}\)，则 \(C\) 的离心率为 ？

得到 \(M(a,a)\implies A(3a-\lambda c,3a),AF_2=2c-a=ex_A-a\)，因此 \(x_A=2a,e=2\)

抛物线

• 概念：平面内与一个定点 \(F\) 和一条定直线 \(l\)（ 不经过点 \(F\) ）的距离相等的点的轨迹叫做抛物线。

标准方程	\(y^2=2px\ (p>0)\)	\(y^2=-2px\ (p>0)\)	\(x^2=2px\ (p>0)\)	\(x^2=-2px\ (p>0)\)
开口方向	向右	向左	向上	向下
焦点坐标	\((\frac{p}{2},0)\)	\((-\frac{p}{2},0)\)	\((0,\frac{p}{2})\)	\((0,-\frac{p}{2})\)
准线	\(x=-\frac{p}{2}\)	\(x=\frac{p}{2}\)	\(y=-\frac{p}{2}\)	\(y=\frac{p}{2}\)

抛物线的离心率 \(e=1\)。

通径：过抛物线的焦点作垂直于对称轴的直线，交抛物线于 \(AB\)，线段 \(AB\) 就是抛物线的通径，长为 \(2p\)，是所有过焦点的弦中最短的。

抛物线焦点弦的性质

\(AB\) 为过抛物线 \(y^2=2px\ (p>0)\) 的焦点 \(F(\frac{p}{2},0)\) 的弦，点 \(A(x_1,y_1),B(x_2,y_2)\) 在准线上的射影分别为点 \(A_1(-\frac{p}{2},y_1),B_1(-\frac{p}{2},y_2)\)。

1. \(|AF|=|AA_1|=x_1+\frac{p}{2},|BF|=|BB_1|=x_2+\frac{p}{2},|AB|=x_1+x_2+p\)。

2. \(x_1x_2=\frac{p^2}{4},y_1y_2=-p^2\)。

证明：当直线 \(AB\) 的斜率存在时，设 \(AB:y=k(x-\frac{p}{2}),k\neq 0\)，联立抛物线方程和直线方程得 \(y^2-\frac{2p}{k}y-p^2=0\)。

易知 \(\Delta>0\)，所以 \(y_1y_2=-p^2,x_1x_2=\frac{y_1^2}{2p}\frac{y_2^2}{2p}=\frac{p^2}{4}\)，同理可证直线 \(AB\) 的斜率不存在时，命题也成立。

3. 以 \(|AB|\) 为直径的圆与抛物线的准线相切。

证明：设 \(AB\) 中点为 \(D\)，\(D\) 到准线的距离为 \(d\)，则 \(d=\frac{|AA_1|+|BB_1|}{2}=\frac{|AB|}{2}\)，原命题得证。

4. 以 \(|AF|\) 为直径的圆与 \(y\) 轴相切。

5. \(\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{p}\)

证明：当直线 \(AB\) 的斜率存在时，\(\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{1}{|AA_1|}+\frac{1}{|BB_1|}=\frac{1}{x+\frac{p}{2}}+\frac{1}{x_2+\frac{p}{2}}=\frac{x_1+x_2+p}{x_1x_2+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{x_1+x_2+p}{\frac{p^2}{4}+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{2}{p}\)

同理可证直线 \(AB\) 的斜率不存在时，命题也成立。

6. 若直线 \(AB\) 的倾斜角为 \(\alpha\)，则 \(|AB|=\frac{2p}{\sin^2\alpha}\)

证明：当直线 \(AB\) 的斜率存在时，设 \(AB:y=k(x-\frac{p}{2}),k\neq 0\)，由 \(\begin{cases} y=k(x-\frac{p}{2}) \\ y^2=2px\end{cases}\) 得 \(ky^2-2py-kp^2=0\)。

易知 \(\Delta>0,y_1+y_2=\frac{2p}{k},y_1y_2=-p^2,|AB|=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]}=\sqrt{1+\frac{1}{k^2}}\cdot\frac{2p\sqrt{1+k^2}}{|k|}=\frac{2p(1+k^2)}{k^2}=\frac{2p(1+\tan^2\alpha)}{\tan^2\alpha}=\frac{2p}{\sin^2\alpha}\)

当直线 \(AB\) 的斜率不存在时，\(|AB|=2p=\frac{2p}{\sin^2 90\degree}\)，命题也成立。

推广：\(|AF|=\frac{p}{1-\cos\alpha},|BF|=\frac{p}{1+\cos\alpha}\)，\(O\) 到 \(AB\) 的距离 \(=\frac{p\sin\alpha}{2},S_{\Delta AOB}=\frac{p^2}{2\sin\theta}\)

注：若抛物线为 \(x^2=\pm 2py\)，将上述 \(\cos\) 换为 \(\sin\)，\(\sin\) 换为 \(\cos\)。

7. \(A,O,B_1\) 三点共线，\(A_1,O,B\) 三点共线。

设 \(AB:x=my+\frac{p}{2}\) 即可通过斜率相等证明。

8. \(A_1F\perp B_1F\)

9. 对于 \(y^2=2px(p>0)\)，当直线过点 \((a,0)\) 与抛物线交于 \(P,Q\)，则 \(k_{OP}k_{OQ}=-\frac{2p}{a}\)。

10. 对于 \(y^2=2px\)，\(AB\) 为其一条弦，则 \(k_{AB}=\frac{2p}{y_1+y_2}\)；对于 \(x^2=2py\)，则 \(k_{AB}=\frac{x_1+x_2}{2p}\)。

11. 对于 \(x^2=2py\)，过其上一点 \(P(x_1,y_1)\) 做切线 \(y=kx+(y_1-kx_1)\)，联立得 \(\Delta=pk^2-2x_1k+2y_1=0\implies k=\frac{x_1}{p}\)，即切线为 \(y=\frac{x_1}{p}-\frac{x_1^2}{2p}\)。

好题

1. 过点 \(Q(4,1)\) 作抛物线 \(y^2=8x\) 的弦 \(AB\)，恰被点 \(Q\) 平分，则弦 \(AB\) 所在直线的方程为 ？

（ 点差法 ）解：设 \(A(x_1，y_1),B(x_2,y_2)\)，则 \(\begin{cases} y_1^2=8x_1 (1) \\ y_2^2=8x_2 (2)\end{cases}\)，因为 \(Q(4,1)\) 是 \(AB\) 中点，所以 \(\begin{cases} x_1+x_2=8 \\ y_1+y_2=2 \end{cases}(3)\)

\((1)-(2)\) 得 \((y_1+y_2)(y_1-y_2)=8(x_1-x_2)\ \ \ \text{}\) 把 \((3)\) 代入得 \(\frac{y_1-y_2}{x_1-x_2}=4\)，所以 \(AB:y=4x-15\)。

---

2. 已知抛物线 \(C:y^2=4x\) 的焦点为 \(F\)，直线 \(l\) 过焦点 \(F\) 与 \(C\) 交于 \(A,B\) 两点，以 \(AB\) 为直径的圆与 \(y\) 轴交于 \(D,E\) 两点，且 \(|DE|=\frac{4}{5}|AB|\)，则直线 \(l\) 的方程为_____

解：设 \(|AB|=2r(2r\geq 4)\)，\(AB\) 的中点为 \(M\)，作 \(MN\perp y\) 轴于点 \(N\)，过 \(A,B\) 分别作准线 \(l:x=-1\) 的垂线，垂足为 \(A_1,B_1\)

显然 \(2(|MN|+1)=|AA_1|+|BB_1|=|AF|+|BF|=|AB|=2r\)，所以 \(|MN|=r-1,|DE|=2\sqrt{r^2-(r-1)^2}=\frac{8}{5}r\)

解得 \(r=\frac{5}{2}\ \text{or}\ \frac{5}{8}\)（ 舍 ），所以 \(M_x=\frac{3}{2}\ \ \ \text{}\) 设直线 \(l:y=k(x-1),A(x_1,y_1),B(x_2,y_2)\)。

联立 \(\begin{cases} y=k(x-1) \\ y^2=4x\end{cases}\) 得 \(k^2x^2-(2k^2+4)x+k^2=0\implies x_1+x_2=\frac{2k^2+4}{k^2}=3\)，解得 \(k=\pm 2\)。

故直线 \(l\) 的方程为 \(2x\pm y-2=0\)。

---

3. （ 多选 ）已知点 \(F\) 是抛物线 \(y^2=2px\ (p>0)\) 的焦点，\(AB,CD\) 是经过点 \(F\) 的弦，且 \(AB\perp CD\)，直线 \(AB\) 的斜率为 \(k\) 且 \(k>0\)，\(A,C\) 两点在 \(x\) 轴上方，以下一定成立的有（ ）

   \(\text{A.}\ \frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{B.}\) 若 \(|AF|\cdot|BF|=\frac{4}{3}p^2\)，则 \(k=\frac{\sqrt{3}}{3}\)

   \(\text{C.}\ \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OC}\cdot\overrightarrow{OD}\ \ \ \ \ \ \ \ \text{D.}\) 四边形 \(ACBD\) 面积的最小值为 \(16p^2\)

答案：\(\text{AC}\)

解析：\(\text{A.}\) 由题得 \(k_{CD}=-\frac{1}{k}\)，设 \(AB:y=k(x-\frac{p}{2})\)，联立 \(\begin{cases} y=k(x-\frac{p}{2}) \\ y^2=2px\end{cases}\) 得

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{}\) \(k^2x^2-p(k^2+2)x+\frac{1}{4}k^2p^2=0\implies x_1+x_2=\frac{p(k^2+2)}{k^2},x_1x_2=\frac{1}{4}p^2\implies |AB|=x_1+x_2+p=\frac{2p(k^2+1)}{k^2}\)

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{}\) 同理 \(|CD|=2p(1+k^2)\)，则有 \(\frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p}\)

\(\ \ \ \ \ \ \ \ \ \text{}\) \(\text{B.}\) \(|AF|\cdot|BF|=(x_1+\frac{p}{2})(x_2+\frac{p}{2})=p^2+\frac{p^2}{k^2}=\frac{4}{3}p^2\implies k=\sqrt{3}\)

\(\ \ \ \ \ \ \ \ \ \text{}\) \(\text{C.}\) \(\overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=\frac{1}{4}p^2+k^2(x_1-\frac{p}{2})(x_2-\frac{p}{2})=-\frac{3}{4}p^2\)，与 \(k\) 无关，同理 \(\overrightarrow{OC}\cdot\overrightarrow{OD}=-\frac{3}{4}p^2\)

\(\ \ \ \ \ \ \ \ \ \text{}\) \(\text{D.}\) 因为 \(AB\perp CD\) 所以 \(S=\frac{1}{2}|AB|\cdot|CD|=\frac{1}{2}\frac{2p(k^2+1)}{k^2}\cdot 2p(1+k^2)=2p^2(k^2+\frac{1}{k^2}+2)\geq 8p^2\) 当且仅当 \(k=1\) 取等。

---

（ 同构 ）4. （ \(2011\) 浙江卷 ）已知抛物线 \(C_1:x^2=y\)，圆 \(C_2:x^2+(y-4)^2=1\) 的圆心为点 \(M\)。已知 \(P\) 是抛物线 \(C_1\) 上的点（ 异于原点 ），过点 \(P\) 作圆 \(C_2\) 的两条切线，分别交 \(C_1\) 于点 \(A,B\)，若过点 \(M,P\) 两点的直线 \(l\) 垂直于 \(AB\)，求直线 \(l\) 的方程。

设 \(P(x_0,x_0^2),A(x_1,x_1^2),B(x_2,x_2^2)\)，则 \(k_{AB}=x_1+x_2\)，\(PA:y-x_0^2=(x_1+x_0)(x-x_0)\)，即 \((x_1+x_0)x-y-x_1x_0=0\)。

从而 \(1=\frac{|4+x_1x_0|}{\sqrt{(x_1+x_0)^2+1}}\)，整理得 \((1-x_0^2)x_1^2-6x_1x_0+x_0^2-15=0\)，同理 \((1-x_0^2)x_2^2-6x_2x_0+x_0^2-15=0\)。

显然 \(x_1,x_2\) 是方程 \((1-x_0^2)x^2-6xx_0+x_0^2-15=0\) 的两根，\(x_1+x_2=\frac{6x_0}{1-x_0^2}=k_{AB}\)，因为 \(k_l=\frac{x_0^2-4}{x_0}\)。

所以可以解得 \(x_0^2=\frac{23}{5},l:y=\pm\frac{3\sqrt{115}}{115}x+4\)。

---

（ 向量 ）5. 已知抛物线 \(y=x^2,A(-\frac{1}{2},\frac{1}{4}),B(\frac{3}{2},\frac{9}{4})\)，抛物线上的 \(P(x,y)(-\frac{1}{2}<x<\frac{3}{2})\)，过点 \(B\) 作直线 \(AP\) 的垂线，垂足为 \(Q\)，求 \(|PA|\cdot|PQ|\) 的最大值。

设 \(AB\) 中点为 \(M(\frac{1}{2},\frac{5}{4})\)，从而 \(|PA|\cdot|PQ|=-\overrightarrow{PA}\cdot\overrightarrow{PQ}=-\overrightarrow{PA}\cdot(\overrightarrow{PB}+\overrightarrow{BQ})=-\overrightarrow{PA}\cdot\overrightarrow{PB}=(\frac{\overrightarrow{PA}-\overrightarrow{PB}}{2})^2-(\frac{\overrightarrow{PA}+\overrightarrow{PB}}{2})^2=2-|PM|^2=(x+\frac{1}{2})^3(\frac{3}{2}-x)=\frac{1}{3}(x+\frac{1}{2})(x+\frac{1}{2})(x+\frac{1}{2})(\frac{9}{2}-3x)\leq \frac{1}{3}[\frac{(x+\frac{1}{2})+(x+\frac{1}{2})+(x+\frac{1}{2})+(\frac{9}{2}-3x))}{4}]^4\leq\frac{27}{16}\)。

当且仅当 \(x=1\) 时取等号。

---

（ 齐次化 ）6. 抛物线 \(C:y^2=2px\)，设 \(A,B\) 为抛物线上的点，\(OA\perp OB\)，证明 \(AB\) 过定点。

设 \(AB:mx+ny=1\)，联立 \(y^2=2px(mx+ny)\implies y^2-2pnxy-2pmx^2=0\)，同时除以 \(x^2\) 得：

\((\frac{y}{x})^2-2pn\frac{y}{x}-2pm=0\implies\frac{y_1}{x_1}\frac{y_2}{x_2}=-2pm=-1\)，得 \(2pm=1\)，因此定点为 \((2p,0)\)。

其他问题

共焦点问题

已知 \(F_1,F_2\) 为椭圆（ 离心率 \(e_1\) ）和双曲线（ 离心率 \(e_2\) ）的公共焦点，\(P\) 是一个公共点，\(\angle F_1PF_2=\theta\)，则 \(\boxed{\frac{\sin^2\frac{\theta}{2}}{e_1^2}+\frac{\cos^2\frac{\theta}{2}}{e_2^2}=1}\)，因此可以推出 \(e_1e_2\geq 2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=\sin\theta\)。

极点极线问题

设圆锥曲线 \(C:Ax^2+By^2+Cxy+Dx+Ey+F=0\)，平面上任意一点 \(P(x_0,y_0)\)，则极点 \(P\) 关于 \(C\) 的极线方程是 \(Ax_0x+By_0y+C\frac{x_0y+y_0x}{2}+D\frac{x_0+x}{2}+E\frac{y_0+y}{2}+F=0\)。也就是说：

1. \(x^2,y^2\) 换成 \(x_0x,y_0y\)。
2. \(xy\) 换成 \(\frac{x_0y+y_0x}{2}\)。
3. \(x,y\) 换成 \(\frac{x_0+x}{2},\frac{y_0+y}{2}\)。
4. 常数项不变。

对于椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\)，\(P\) 的极线方程为 \(\boxed{\frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1}\)；当 \(P\) 是焦点时，极线 \(=\) 准线，即 \(x=\frac{a^2}{c}\)

极点 \(P\) 和极线 \(l\) 的【位置关系】满足：

1. \(P\) 在圆锥曲线外，则 \(l\) 为 \(P\) 点处的切点弦方程（ 过 \(P\) 作两条切线，切点的连线 ）。
2. \(P\) 在圆锥曲线上，则 \(l\) 为 \(P\) 点处的切线方程。
3. \(P\) 在圆锥曲线上，则 \(l\) 为与圆锥曲线相离的一条直线（ 虚切点弦方程，过 \(P\) 作弦，再做交点的两条切线，切线的交点的轨迹方程 ）。
   
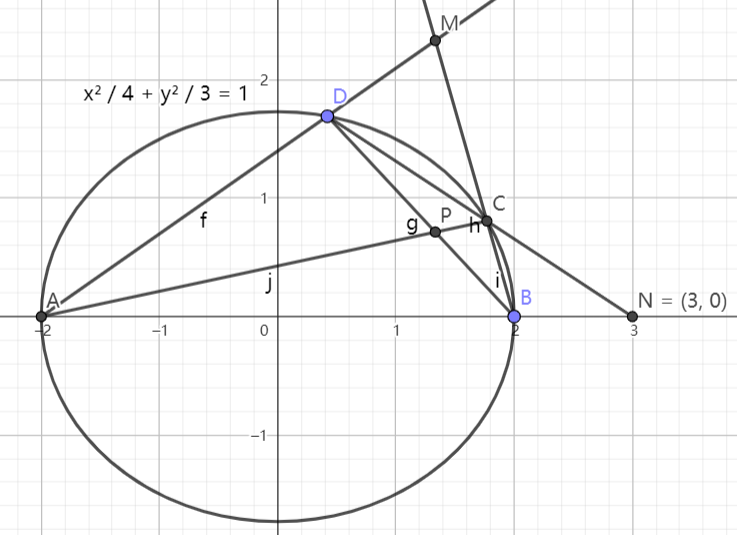
   【部分证明】
   设 \(CD:x=ty+m,C(x_1,y_1),D(x_2,y_2),N(m,0)\)，则 \(y_1+y_2=\frac{-2b^2mt}{a^2+b^2t^2},y_1y_2=\frac{b^2m^2-a^2b^2}{a^2+b^2t^2}\)

注意到 \(\displaystyle m(y_1+y_2)+2ty_1y_2=\frac{-2a^2b^2t}{a^2+b^2t^2}=\frac{a^2}{m}(y_1+y_2)\)

有 \(AC:x=\frac{x_1+a}{y_1}y-a,BD:x=\frac{x_2-a}{y_2}y+a\)，联立得

\[\frac{ty_1+m+a}{y_1}y-a=\frac{ty_2+m-a}{y_2}y+a\implies\frac{m+a}{y_1}y-\frac{m-a}{y_2}y=2a \]

\[\begin{aligned}y_M&=\frac{2ay_1y_2}{m(y_2-y_1)+a(y_1+y_2)}\\x_M&=\frac{a^2(y_2-y_1)+2aty_1y_2+am(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}\\&=\frac{a^2(y_2-y_1)+a\cdot\frac{a^2}{m}(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}=\frac{a^2}{m}\end{aligned} \]

【性质】

过 \(P\) 作直线 \(PQ\)，交极线 \(MN\) 于 \(Q\)，交椭圆于 \(A,B\) 两点 \(\iff\frac{|PA|}{|PB|}=\frac{|QA|}{|QB|}\)（ 调和点列 ）。

【例题】

设 \(C:\frac{x^2}{4}+\frac{y^2}{3}=1\)，过 \(C\) 的右焦点，且斜率不为 \(0\) 的直线交 \(C\) 于 \(M,N\) 两点，直线 \(AM,BN\) 交于点 \(Q\)，证明：点 \(Q\) 在直线 \(x=4\) 上。

解：显然右焦点 \((1,0)\) 是极点，那么极线就是 \(\frac{x}{4}=1\)，即 \(x=4\)。

与定值 \(\frac{2}{e}\) 有关的问题：

1. 若 \(AB\) 是过椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 的焦点 \(F\) 的焦点弦，\(AB\) 的垂直平分线交 \(x\) 轴于点 \(M\)，则 \(\frac{|AB|}{|FM|}\) 为定值 \(\frac{2}{e}\)。

证明：设 \(F\) 为左焦点，以 \(F\) 为极点，\(x\) 轴为极轴建立极坐标系，得极坐标方程 \(\rho = \frac{ep}{1-e\cos\theta}\)，

所以 \(|AB|=\rho_1+\rho_2=\frac{2ep}{1-e^2\cos^2\theta}\)，\(|FM|=\frac{1}{|\cos\theta|}|\frac{\rho_1-\rho_2}{2}|=\frac{e^2p}{1-e^2\cos^2\theta}\implies\frac{|AB|}{|FM|}=\frac{2}{e}\)

2. 椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 的左焦点为 \(F\)，在 \(x\) 轴上点 \(F\) 右侧有一点 \(A\)，以 \(FA\) 为直径作半径为 \(R\) 的圆，在 \(x\) 轴上方部分交于 \(N,M\) 两点，则 \(\frac{|FM|+|FN|}{R}=\frac{2}{e}\)

证明：设圆为 \([x-(R-c)]^2+y^2=R^2\)，联立得 \(x_1+x_2=\frac{2a^2(R-c)}{c^2},|FM|+|FN|=a+ex_1+a+ex_2=\frac{2R}{e}\)

3. 若 \(AB\) 为椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 焦点 \(F\) 的弦，\(FM\) 为与焦点 \(F\) 对应的焦准距，则 \(\frac{|AB||FM|}{|FA||FB|}=\frac{2}{e}\)

证明：同 1 建极坐标系，\(|FM|=p,|FA|=\frac{ep}{1-e\cos\theta},|FB|=\frac{ep}{1+e\cos\theta},|AB|=|FA|+|FB|=\frac{2ep}{1-e^2\cos^2\theta},|FA||FB|=\frac{e^2p^2}{1-e^2\cos^2\theta}\)。

4. 已知椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 的左右焦点分别为 \(F_1,F_2,A(-a,0),B(a,0)\)，点 \(P\) 是椭圆上的点（ 不与 \(A,B\) 重合 ），\(\angle APB=2\alpha,\angle F_1PF_2=2\beta,|\tan\beta\tan 2\alpha|\) 为定值 \(\frac{2}{e}\)

光学性质

【椭圆】：设 \(F_1,F_2\) 是椭圆的两个焦点，从 \(F_1\) 出发的光线经过反射必经过 \(F_2\)。

【双曲线】：设 \(F_1,F_2\) 是双曲线的两个焦点，从 \(F_1\) 出发的光线经过反射后的反向延长线必经过 \(F_2\)。

【抛物线】：设 \(F\) 为焦点，从 \(F\) 出发的光线经过反射后，平行于对称轴。

【椭圆+抛物线】设 \(P\) 为反射点，\(AB\) 为 \(P\) 处的切线，\(PT\) 平分 \(\angle F_1PF_2\)，则 \(PT\perp AB\)

仿射变换

设 \(a>0,b>0\)，将原来曲线上的每个点的横坐标乘以 \(a\)，纵坐标乘以 \(b\)，形成了新的曲线。

【性质】：

1. 对原来的两条曲线作仿射变换，交点数不变。
2. 对曲线 \(f(x,y)=0\) 作仿射变换，曲线变为 \(f(\frac{x}{a},\frac{y}{b})=0\)。
3. 对面积为 \(S\) 的曲线作仿射变换，面积变为 \(abS\)。
4. 对直线 \(Ax+By+C=0\) 作仿射变换，变为 \(\frac{A}{a}x+\frac{B}{b}y+C=0\)

【推论】

1. 椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 与直线 \(Ax+By+C=0\) 相切的充要条件是 \(A^2a^2+B^2b^2=C^2\)。
2. 椭圆面积为 \(\pi ab\)

阿基米德三角形

圆锥曲线的弦和过弦端点的两条切线所围成的三角形称为阿基米德三角形，该弦称为底边。

【2006高考卷】已知抛物线 \(x^2=4y\) 的焦点为 \(F\)，点 \(A,B\) 是抛物线上两个动点，且 \(\overrightarrow{AF}=\lambda\overrightarrow{FB}(\lambda>0)\)，过 \(A,B\) 两点分别作抛物线的切线，设其交点为 \(M\)，证明：\(\overrightarrow{FM}\cdot\overrightarrow{AB}\) 是定值。

解：设 \(A(x_1,\frac{x_1^2}{4}),B(x_2,\frac{x_2^2}{4})\)，由 \(\overrightarrow{AF}=\lambda\overrightarrow{FB}\) 得 \(x_1x_2=-4\)。

已知抛物线方程为 \(y=\frac{1}{4}x^2\)，求导得 \(y`=\frac{1}{2}x\)，所以过 \(A,B\) 两点的切线方程是 \(y=\frac{1}{2}x_1x-\frac{1}{4}x_1^2,y=\frac{1}{2}x_2x-\frac{1}{4}x_2^2\)

交点 \(M(\frac{x_1+x_2}{2},-1)\)，所以 \(\overrightarrow{FM}=(\frac{x_1+x_2}{2},-2),\overrightarrow{AB}=(x_2-x_1,\frac{x_2^2-x_1^2}{4})\)，从而 \(\overrightarrow{FM}\cdot\overrightarrow{AB}=0\)

扩展开来，对于抛物线 \(y^2=2px(p>0)\) 的焦点 \(F\) 的直线交抛物线于 \(A,B\) 两点，过 \(A,B\) 两点的切线交于 \(M\)，则 \(\boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0}\)，并且 \(M\) 在准线上，并且 \(\boxed{|MF|^2=|FA|\cdot|FB|}\)。（ 证明 \(MA\perp MB\) 即可，射影定理 ）

对于椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 的左焦点 \(F\) 任意做一条直线 \(AB\)，交椭圆于 \(A,B\) 两点，分别过 \(A,B\) 作椭圆的切线交于点 \(M\)，则 \(M\) 在左准线上，且 \(\boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0}\)。（ 通过设 \(A(a\cos\theta_1,b\sin\theta_1)\) 等证明 ）

柯西不等式

引理

设 \(\overrightarrow{a}=(x_1,y_1),\overrightarrow{b}=(x_2,y_2)\)，由 \(|\overrightarrow{a}|\cdot|\overrightarrow{b}|\geq\overrightarrow{a}\cdot\overrightarrow{b}\)

得 \((x_1^2+y_1^2)\cdot(x_2^2+y_2^2)\geq(x_1x_2+y_1y_2)^2\)，当且仅当 \(\frac{x_1}{x_2}=\frac{y_1}{y_2}\) 时等号成立。

例题

1. 设椭圆 \(C:\frac{x^2}{16}+\frac{y^2}{12}=1,M(2,\sqrt{2})\)，过点 \(P(-8,0)\) 的直线与 \(C\) 交于 \(A,B\) 两点，求 \(\Delta ABF\) 面积的最大值。

设 \(A(x_1,y_1),B(x_2,y_2)\)，由 \(P,A,B\) 三点共线得 \(k_{PA}=k_{PB}\implies\frac{y_1}{x_1+8}=\frac{y_2}{x_2+8}\implies x_2y_1-x_1y_2=8(y_2-y_1)\)

\[\begin{aligned} S_{\Delta ABF}&=S_{\Delta PBF}-S_{\Delta PAF}=\frac{1}{2}|PF||y_1-y_2| \\ &=\frac{1}{2}\times 6\times |y_1-y_2|=\frac{3}{8}|x_1y_2-x_2y_1| \\ &\leq\frac{3}{8}\sqrt{12\times 16\times (\frac{x_1^2}{16}+\frac{y_1^2}{12})[\frac{y_2^2}{12}+\frac{(-x_2)^2}{16}]} \\ &=3\sqrt{3} \end{aligned}\]

当且仅当 \(\frac{x_1x_2}{4}=-\frac{y_1y_2}{3}\) 时成立。

2. 【天津静海四校 2021 阶段性检测】已知 \(E:\frac{x^2}{4}+y^2=1,A(-2,0),B(0,1),F_1(-\sqrt{3},0),F_2(\sqrt{3},0),P\) 为椭圆上一动点。\(C,D\) 是 \(E\) 上两个不同的点，\(CD//AB\)，直线 \(CD\) 与 \(x,y\) 轴分别交于 \(M,N\) 两点，且 \(\overrightarrow{MC}=\lambda\overrightarrow{CN},\overrightarrow{MD}=\mu\overrightarrow{DN}\)，求 \(\lambda+\mu\) 的取值范围。

显然 \(k_{AB}=\frac{1}{2}\)，可设 \(CD\) 的方程为 \(y=\frac{1}{2}x+m(m\neq\pm 1)\)，得 \(M(-2m,0),N(0,m)\)，设 \(C(x_1,y_1),D(x_2,y_2)\)

由 \(\overrightarrow{MC}=\lambda\overrightarrow{CN}\)，得 \((x_1+2m,y_1)=\lambda(-x_1,m-y_1)\implies\begin{cases}x_1=\frac{-2m}{1+\lambda} \\ y_1=\frac{\lambda m}{1+\lambda}\end{cases}\)

代入椭圆方程并化简得 \((m^2-1)\lambda^2-2\lambda+m^2-1=0\)，把 \(\lambda\) 换成 \(\mu\) 得到同构方程，因此 \(\lambda,\mu\) 可看成 \((m^2-1)x^2-2x+m^2-1=0\) 的两根。

得到 \(\lambda+\mu=\frac{2}{m^2-1}\)，因为 \(C,D\) 都在 \(E\) 上，由柯西不等式

\[2=(\frac{x^2}{4}+y^2)[(-1)^2+1]\geq(-\frac{1}{2}x+y)^2=m^2 \]

当且仅当 \(C,D\) 重合时等号成立，与题意不符，故 \(0\leq m^2<2\) 且 \(m^2\neq 1\)，所以 \(\lambda+\mu=\frac{2}{m^2-1}\in(-\infty,-2]\cup(2,\infty)\)

拉格朗日恒等式

椭圆形式的拉格朗日恒等式

设 \(A(x_1,y_1),B(x_2,y_2)\) 是椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 上非顶点的两点，则：

\[1=(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2})(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2})=(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})^2+\frac{(x_1y_2-x_2y_1)^2}{a^2b^2} \]

引理 - 三角形面积公式

\(\overrightarrow{OA}=(x_1,y_1),\overrightarrow{OB}=(x_2,y_2)\)，则 \(S_{\Delta OAB}=\frac{1}{2}|x_1y_2-x_2y_1|\)

因此，拉格朗日恒等式可用于处理三角形面积定值问题。当 \((\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})^2=0\) 时，\(S_{\max}=\frac{ab}{2}\)

引理 - 和积关系 & 合比关系

已知 \(A(x_1,y_1),B(x_2,y_2)\) 在椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\) 上，直线 \(AB\) 经过 \(M(m,0)\) 满足：

\[2x_1x_2=(\frac{a^2}{m}+m)(x_1+x_2)-2a^2 \]

直线 \(AB\) 经过 \(N(0,n)\) 满足：

\[2y_1y_2=(\frac{b^2}{n}+n)(y_1+y_2)-2b^2 \]

可用点差法证明。

例题

1. 椭圆 \(E:\frac{x^2}{16}+\frac{y^2}{4}=1,P(0,1),Q(0,2)\)，过点 \(P\) 的直线 \(l:y=kx+1\) 交椭圆 \(E\) 于 \(A,B\) 两点，求 \(S_{\Delta ABQ}\) 最大值。

由 \(A,B,P\) 三点共线得 \(\frac{y_1-1}{x_1}=\frac{y_2-1}{x_2}\)，得

\[(1)\ \ \ \ \ x_1y_2-x_2y_1=x_1-x_2 \]

\[(2)\ \ \ \ \ 2y_1y_2=5(y_1+y_2)-8 \]

\[(3)\ \ \ \ \ x_1x_2=-6(y_1+y_2) \]

由 \((y_1+y_2)^2-(y_1-y_2)^2=4y_1y_2\) 和 \((2)\) 得 \((y_1+y_2)^2-(y_1-y_2)^2=10(y_1+y_2)-16\)

配方得 \((y_1+y_2-5)^2=9+(y_1-y_2)^2\geq 9\)

所以 \(y_1+y_2\leq 2\) 当且仅当 \(y_1=y_2=1\) 时成立（ \(y_1+y_2\geq 8\) 舍去 ）

由拉格朗日恒等式得

\[\begin{aligned} 1&=(\frac{x_1x_2}{16}+\frac{y_1y_2}{4})^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\ &=(\frac{y_1+y_2}{4}-1)^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\ &\geq \frac{1}{4}+\frac{(x_1y_2-x_2y_1)^2}{64} \end{aligned}\]

得 \(|x_1y_2-x_2y_1|\leq 4\sqrt{3}\)，所以 \(S=\frac{1}{2}|PQ||x_1-x_2|=\frac{1}{2}|x_1y_2-x_2y_1|\leq 2\sqrt{3}\)

2. 已知椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\)，\(A,B\) 是其上两动点，\(k_{OA}\cdot k_{OB}=-\frac{b^2}{a^2}\)，点 \(M\) 满足 \(\overrightarrow{OM}=\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}\) 且 \(\lambda^2+\mu^2=1\)，证明 \(M\) 在椭圆上。

设 \(A(x_1,y_1),B(x_2,y_2)\)，易得 \(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2}=0\)，点 \(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1,\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1\)

因此 \(M(\lambda x_1+\mu x_2,\lambda y_1+\mu y_2)\)，代入椭圆方程联立得

\[\lambda^2(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2})+\mu^2(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2})+2\lambda\mu(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})=1 \]

得到 \(\lambda^2+\mu^2=1\)，结论成立。（ 每一步都是等价关系 ）

参数方程

曲线方程	参数方程	三角消元
直线 \(y-y_0=\tan\alpha(x-x_0)(\alpha\) 为倾斜角 \()\)	\(\begin{cases}x=x_0+t\cos\alpha \\ y=y_0+t\sin\alpha\end{cases}(t\) 为参数 \()\)	\(P(x_0+t\cos\alpha,y_0+t\sin\alpha)\)
圆 \((x-a)^2+(y-b)^2=r^2(r>0)\)	\(\begin{cases}x=r\cos\alpha+a \\ y=r\sin\alpha+b\end{cases}(\alpha\) 为参数 \()\)	\(P(r\cos\alpha+a,r\sin\alpha+b)\)
椭圆 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\)	\(\begin{cases}x=a\cos\alpha \\ y=b\sin\alpha\end{cases}(\alpha\) 为参数 \()\)	\(P(a\cos\alpha,b\sin\alpha)\)
双曲线 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\)	\(\begin{cases}x=\frac{a}{\cos\alpha} \\ y=b\tan\alpha\end{cases}(\alpha\) 为参数 \()\)	\(P(\frac{a}{\cos\alpha},b\tan\alpha)\)

本质就是利用 \(\sin^2\alpha+\cos^2\alpha=1\)。

例题

1. 过椭圆 \(C:\frac{x^2}{4}+\frac{y^2}{9}=1\) 上一点 \(P\) 作与直线 \(l:2x+y-6=0\) 夹角为 \(30\degree\) 的直线，交于 \(A\)，求 \(|PA|\) 的最值。

设 \(P(2\cos\theta,3\sin\theta)\)，距离 \(d(P,l)=\frac{\sqrt{5}}{5}|4\cos\theta+3\sin\theta-6|\)，

则 \(|PA|=\frac{d}{\sin 30\degree}=\frac{2\sqrt{5}}{5}|5\sin(\theta+\alpha)-6|\)，其中 \(\alpha\) 为锐角。所以最值为 \(\frac{2\sqrt{5}}{5}\) 和 \(\frac{22\sqrt{5}}{5}\)。

2. 椭圆 \(C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\)，\(A,B,C\) 为其上三点，满足 \(\Delta ABC\) 的重心坐标为 \(O\)，求 \(S_{\Delta ABC}\)。

设 \(A(a\cos\alpha,b\sin\alpha),B(a\cos\beta,b\sin\beta)\implies C(-a(\cos\alpha+\cos\beta),-b(\sin\alpha+\sin\beta))\)，代入得

\((\cos\alpha+\cos\beta)^2+(\sin\alpha+\sin\beta)^2=2+2\cos\alpha\cos\beta+2\sin\alpha\sin\beta=2+2\cos(\alpha-\beta)=1\implies\cos(\alpha-\beta)=-\frac{1}{2}\implies\alpha-\beta=120\degree\)

\(|AB|=\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}\)

\(AB:y=\frac{b(\sin\alpha-\sin\beta)}{a(\cos\alpha-\cos\beta)}(x-a\cos\alpha)+b\sin\alpha\implies b(\sin\beta-\sin\alpha)x+a(\cos\alpha-\cos\beta)y+ab\sin(\alpha-\beta)=0\)

\(d(O,AB)=\frac{\frac{\sqrt{3}}{2}ab}{\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}}\)

由重心性质，\(S_{\Delta ABC}=3S_{\Delta AOB}=\frac{3}{2}|AB|d=\frac{3\sqrt{3}}{4}ab\)。

• 扩展开来，对于平行四边形 \(OABC\)，其中 \(A,B,C\) 三点都在椭圆上，则 \(S=2S_{\Delta AOB}=\frac{\sqrt{3}}{2}ab\)。

数列

• 等差数列通项公式：\(a_n=a_1+(n-1)d=S_n-S_{n-1}(n\geq 2)\), 其中 \(d\) 为公差。

• 等差数列前 \(n\) 项和：\(S_n=\frac{n(a_1+a_n)}{2}=na_1+\frac{dn(n-1)}{2}\)

• 等比数列通项公式：\(a_n=a_1q^{n-1}=S_n-S_{n-1}(n\geq 2)\), 其中 \(q\) 为公比。

• 等比数列前 \(n\) 项和：\(S_n=\frac{a_1(1-q^n)}{1-q}=\frac{a_1-a_n q}{1-q}(q\neq 1)\)

• 自然数幂求和公式：\(\displaystyle\sum_{i=1}^{n}i=\frac{n(n+1)}{2}\)

  \(\displaystyle\sum_{i=1}^{n}i^2=\frac{n(n+1)(2n+1)}{6}\)

  \(\displaystyle\sum_{i=1}^{n}i^3=[\frac{n(n+1)}{2}]^2\)

  \(\displaystyle\sum_{i=1}^{n}i^4=\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}\)

  \(1+3+5+\dots+(2n-1)=n^2\)

求数列通项公式

累加法

条件：形如 \(a_{n+1}=a_n+f(n)\) 且 \({f(n)}\) 可求和。

例题：已知 \(a_1=1,a_{n+1}=a_n+2\)，求 \({a_n}\) 通项公式。

由已知得 \(a_{n+1}-a_n=2,a_n-a_{n-1}=2,\dots,a_2-a_1=2\)，将它们全部相加得到 \(a_{n+1}-a_1=a_{n+1}-1=2n\)，即 \(a_{n}=2n-1\)。

验证 \(a_1\) 也符合上式，因此 \(a_n=2n-1\)。

累乘法

形如 \(a_{n+1}=f(n)a_n\) 且 \({f(n)}\) 可求积。

例题：\(a_1=1,(n+1)a_{n+1}=na_n\)，求 \({a_n}\) 通项公式。

\(\frac{a_{n+1}}{a_n}=\frac{n}{n+1}\implies a_n=\frac{a_n}{1}=\frac{a_n}{a_1}=\frac{a_n}{a_{n-1}}\frac{a_{n-1}}{a_{n-2}}\dots\frac{a_2}{a_1}=\frac{n-1}{n}\frac{n-2}{n-1}\dots\frac{1}{2}=\frac{1}{n}\)

验证 \(a_1\) 也符合上式，因此 \(a_n=\frac{1}{n}\)。

\(a_n=S_n-S_{n-1}\)

例题：\(S_n=3^n+k\)，求 \(a_n\) 通项公式。

\(a_1=3+k,\ \ a_n=S_n-S_{n-1}=3^n-3^{n-1}=2\times 3^{n-1}\)

裂项

\[\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1} \]

\[\frac{1}{n(n+1)(n+2)}=\frac{1}{2}[\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)}] \]

\[\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1}) \]

\[\frac{1}{\sqrt{a}+\sqrt{b} }=\frac{1}{a-b}(\sqrt{a}-\sqrt{b}) \]

\[\frac{1}{a_na_{n+k} }=\frac{1}{dk}(\frac{1}{a_n}-\frac{1}{a_{n+k} })\ \ \ \ （ 等差数列 ） \]

\[\frac{2^n}{(2^n+1)(2^{n+1}+1)}=\frac{1}{2^n+1}-\frac{1}{2^{n+1}+1} \]

等差数列的性质

• \(\frac{S_n}{n}=\frac{na_1+\frac{n(n-1)d}{2}}{n}=a_1+\frac{n-1}{2}d\)，则 \({\frac{S_n}{n}}\) 是首项为 \(a_1\)，公差为 \(\frac{d}{2}\) 的等差数列。

• 若等差数列的项数为 \(2n\)，则 \(S_{2n}=n(a_n+a_{n+1})\)，且 \(S_{偶}-S_{奇}=nd,\frac{S_{奇}}{S_{偶}}=\frac{a_n}{a_{n+1}}\)

• 若等差数列的项数为 \(2n-1\)，则 \(S_{2n-1}=(2n-1)a_n\)，且 \(S_{偶}-S_{奇}=a_n,\frac{S_{奇}}{S_{偶}}=\frac{n}{n-1}\)

• 等差数列依次每 \(k\) 项之和仍成等差数列，即 \(S_k,S_{2k}-S_k,S_{3k}-S_{2k},\dots,S_{nk},S_{(n-1)k}\) 成等差数列，公差 \(k^2d\)。

• \(S_{2n-1}=\frac{(2n-1)(a_1+a_{2n-1})}{2}=(2n-1)a_n,a_n=\frac{S_{2n-1}}{2n-1}\)。

• 等差数列 \({a_n},{b_n}\) 的前缀和分别为 \(S_n,T_n\)，则 \(\frac{a_n}{b_n}=\frac{S_{2n-1}}{T_{2n-1}}\)。

• \(S_m=p,S_n=q\implies S_{n+m}=\frac{(S_n-S_m)(n+m)}{n-m}=\frac{(q-p)(n+m)}{n-m}\)

  特别的，若 \(S_m=n,S_n=m\)，则 \(S_{n+m}=-(n+m)\)；若 \(S_n=S_m\)，则 \(S_{n+m}=0\)。

等比数列的性质

• 若 \(m+n=r+s(m,n,r,s\in\N^+)\)，则 \(a_ma_n=a_ra_s\)。

• \({a_n}\) 公比为 \(q\implies \lambda a_n\) 公比为 \(q\)，\(\frac{1}{a_n}\) 公比为 \(\frac{1}{q}\)，\(|a_n|\) 公比为 \(|q|\)，\(\lg a_n\) 公比为 \(\lg q\)，\(a_n\pm a_{n+1}\) 公比为 \(q\)；若 \(b_n\) 公比为 \(q'\)，则 \(a_nb_n\) 公比为 \(qq'\)。

  注意 \(q=\pm 1\) 是否满足条件。

• \(a_n\) 的前 \(n\) 项积记为 \(T_n=a_1^n q^{\frac{n(n-1)}{2}}\)，且 \(T_n,\frac{T_{2n}}{T_n},\frac{T_{3n}}{T_{2n}}\) 为公比 \(=q^{n^2}\) 的等比数列，由此可得 \(T_{3n}=(\frac{T_{2n}}{T_n})^3\)。

构造等比数列求通项公式

• 对于 \(a_n=pa_{n-1}+q(p\neq 1,pq\neq 0,n\geq 2)\)，转化为 \(a_n-\frac{q}{1-p}=p(a_{n-1}-\frac{q}{1-p})\)

  也可以通过与 \(a_{n-1}=pa_{n-2}+q\) 相减得 \(a_n-a_{n-1}=p(a_{n-1}-a_{n-2})\)

• 对于 \(a_n=pa_{n-1}+q^{n-1}\)，转化为 \(a_n-\frac{q^n}{q-p}=p(a_{n-1}-\frac{q^{n-1}}{q-p})\)

  也可以同除 \(q^n\) 变成上一点的方法。

• 对于 \(a_n=pa_{n-1}+q^{n-1}+t\)，转化为 \(a_n-\frac{t}{1-p}=p(a_{n-1}-\frac{t}{1-p})+q^{n-1}\)，再用上一点的方法。

数学归纳法

一般地，证明一个与正整数 \(n\) 有关的命题，可按下列步骤进行：

1. （ 归纳奠基 ）证明当 \(n=n_0\) 时命题成立。
2. （ 归纳递推 ）以“当 \(n=k(k\in\N^+,k\geq n_0)\) 时命题成立”为条件推出 “当 \(n=k+1\) 时命题也成立”。

完成以上 \(2\) 个步骤就可以证明命题对从 \(n_0\) 开始的所有正整数 \(n\) 都成立。

例 1：证明 \(\displaystyle\sum_{i=1}^n i^2=\frac{1}{6}n(n+1)(2n+1)(n\in\N^+)\)

（1）当 \(n=1\) 时，\(1^2=1=\frac{1}{6}\cdot 1\cdot 2\cdot 3\)，命题成立。

（2）假设当 \(n=k\) 时，命题成立，那么当 \(n=k+1\) 时有：

\(\displaystyle\sum_{i=1}^{k+1} i^2=\frac{1}{6}k(k+1)(2k+1)+(k+1)^2=\frac{k(k+1)(2k+1)+6(k+1)^2}{6}=\frac{(k+1)(2k^2+7k+6)}{6}=\frac{(k+1)(k+2)(2k+3)}{6}\)

即当 \(n=k+1\) 时，命题也成立。

由 （1）（2） 可知，命题对任意 \(n\in\N^+\) 都成立。

练：证明 \(\displaystyle\sum_{i=1}^n i\times (i+1)^2=\frac{1}{12}n(n+1)(3n^2+11n+10)\)。

例 2：（ 2012 湖北卷 ）

\((1)\) 已知函数 \(f(x)=rx-x^r+(1-r)(x>0,0<r<1)\) 且 \(r\) 为有理数，求 \(f(x)_{\min}\)。

\((2)\) 用 \((1)\) 的结果证明：设 \(a_1,a_2\geq 0,b_1,b_2\) 为正有理数，若 \(b_1+b_2=1\)，则 \(a_1^{b_1}a_2^{b_2}\leq a_1b_1+a_2b_2\)。

\((3)\) 将 \((2)\) 中的命题推广到一般形式并用数学归纳法证明。

解：\((1)\) 求导得 \(f`(x)=0\implies x=1,f(x)_{\min}=f(1)=0\)。

\((2)\) 由 \((1)\) 得当 \(x\in(0,+\infty)\) 时，\(f(x)\geq f(1)=0\)，即 \(x^r\leq rx+(1-r)\)。

若 \(r_1r_2=0\)，则原命题成立。

若 \(r_1r_2\neq 0\)，则 \(b_2=1-b_1\)，令 \(x=\frac{a_1}{a_2},r=b_1\)，得 \((\frac{a_1}{a_2})^{b_1}\leq b_1\cdot \frac{a_1}{a_2}+(1-b_1)\implies a_1^{b_1}a_2^{1-b_1}\leq a_1b_1+a_2(1-b_1)\)，原命题成立。

\((3)\) 推广：\(\displaystyle\sum_{i=1}^n b_i=1\implies \prod_{i=1}^n a_i^{b_i}\leq \sum_{i=1}^n a_ib_i\)

① 当 \(n=1\) 时推广成立。

② 假设 \(n=k\) 时成立，且 \(\displaystyle\sum_{i=1}^k b_i=1\)，则 \(\prod_{i=1}^k a_i^{b_i}\leq \sum_{i=1}^k a_ib_i\)。

当 \(n=k+1\) 时，\(\displaystyle\sum_{i=1}^{k+1} b_i=1\)，于是 \(a_1^{b_1}a_2^{b_2}\dots a_k^{b_k}a_{k+1}^{b_{k+1}}=(a_1^{\frac{b_1}{1-b_{k+1}}}a_2^{\frac{b_2}{1-b_{k+1}}}\dots a_k^{\frac{b_k}{1-b_{k+1}}})a_{k+1}^{b_{k+1}}\)

因 \(\displaystyle\sum_{i=1}^n \frac{b_i}{1-b_{k+1}}=1\)，由归纳假设得 \((a_1^{\frac{b_1}{1-b_{k+1}}}a_2^{\frac{b_2}{1-b_{k+1}}}\dots a_k^{\frac{b_k}{1-b_{k+1}}})\leq\frac{a_1b_1+a_2b_2+\dots a_kb_k}{1-b_{k+1}}\)

又因 \((1-b_{k+1})+b_{k+1}=1\)，得 \((\frac{a_1b_1+a_2b_2+\dots a_kb_k}{1-b_{k+1}})^{1-b_{k+1}}a_{k+1}^{b_{k+1}}\leq\frac{a_1b_1+a_2b_2+\dots+a_kb_k}{1-b_{k+1}}\cdot(1-b_{k+1})+a_{k+1}b_{k+1}\)

从而当 \(n=k+1\) 时，推广成立。

结合 ①②，对于一切正整数 \(n\)，推广命题成立。

导数

基本初等函数的导数公式

\(f(x)\)	\(c\)	\(x^a\)	\(a^x\)	\(\log_a x\)	\(\sin x\)	\(\cos x\)
\(f'(x)\)	\(0\)	\(ax^{a-1}\)	\(a^x\ln a\)	\(\frac{1}{x\ln a}\)	\(\cos x\)	\(-\sin x\)

运算法则

• \([f(x)\pm g(x)]'=f'(x)\pm g'(x)\)

• \([f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)\)

• \([\frac{f(x)}{g(x)}]'=\frac{g(x)f'(x)-f(x)g'(x)}{g^2(x)}(g(x)\neq 0)\)

• \([cf(x)]'=cf'(x)\)

• \([af(x)\pm bg(x)]'=af'(x)\pm bg'(x)\)

• \([\frac{1}{g(x)}]'=-\frac{g'(x)}{g^2(x)}(g(x)\neq 0)\)

• 复合函数 \(y=f(g(x))\) 的导数，与 \(y=f(u), u=g(x)\) 的关系：\(y_x^{'}=y_u^{'}\cdot u_x^{'}\)

  即 \(y\) 对 \(x\) 的导数等于 \(y\) 对 \(u\) 的导数乘 \(u\) 对 \(x\) 的导数。

  例 1：求 \(f(x)=(3x+5)^3\) 的导数 \(f'(x)\)，可以看作 \(y=u^3\) 与 \(u=3x+5\) 的复合函数。

  \(y_x^{'}=y_u^{'}\cdot u_x^{'}=(u^3)'\cdot (3x+5)'=3u^2 \times 3 = 9(3x+5)^2\)

  例 2：求 \(f(x)=e^{-0.05x+1}\) 的导数 \(f'(x)=(e^{u})'\cdot(-0.05x+1)'=-0.05e^{-0.05x+1}\)

  例 3：求 \(f(x)=\ln(2x-1)\) 的导数 \(f'(x)=(\ln{u})'\cdot(2x-1)'=\frac{1}{u}\times 2=\frac{2}{2x-1}\)

重要结论

• \(2\) 个重要极限：\(\displaystyle\lim_{x\to\infty}(1+\frac{1}{x})^x=e,\lim_{x\to 0}\frac{\sin x}{x}=1\)

• 常见的指数放缩：\(e^x\geq x+1(x=0\) 取等\(),e^x\geq ex(x=1\) 取等\()\)

• 常见的对数放缩：\(1-\frac{1}{x}\leq \ln x\leq x-1(x=1\) 取等\(),\ln x\leq \frac{x}{e}(x=e\) 取等\(),x\geq \ln(x+1)(x=0\) 取等\()\)

• 常见的三角放缩：\(\sin x<x<\tan x(x\in(0,\frac{\pi}{2}))\)

统计

简单随机抽样：\(1.\) 个体数有限 \(2.\) 逐个抽取 \(3.\) 被抽到的概率相等。

例：\(10\) 个个体里抽一个容量为 \(n\) 的样本， 某个个体 \(A\) 第一次被抽到的可能性为 ？第二次被抽到的可能性为 ？

第一次：\(\frac{1}{10}\) 第二次：\(\frac{9}{10}\times\frac{1}{9}=\frac{1}{10}\)

随机数表题：范围 \([0,39]\)，有以下随机数表，从第 \(1\) 行第 \(3\) 列开始，选出的数依次为 \(36,33,26,16,11,14,10\)。

\(0347\)	\(4373\)	\(8636\)	\(9647\)	\(3661\)	\(4698\)
\(6371\)	\(6233\)	\(2616\)	\(8045\)	\(6011\)	\(1410\)

总体平均数：\(\bar{x}=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i\ \ \text{}\) 中位数：\(\begin{cases}x_{\lceil\frac{n}{2}\rceil} & x\ \mathrm{mod}\ 2\equiv 1 \\ \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} & x\ \mathrm{mod}\ 2\equiv 0\end{cases}\ \ \text{}\)

众数：出现次数最多的数据，不一定唯一，也不一定有众数。

极差：\(\max{\set{x_i}}-\min{\set{x_i}}\ \ \ \ \text{}\) 标准差：\(s=\sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2}\)

\(\begin{aligned}方差：s^2&=\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2=\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i^2-2x_i\bar{x}+\bar{x}^2)=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i^2-\frac{1}{n}\displaystyle\sum_{i=1}^{n}2x_i\bar{x}+\frac{1}{n}\displaystyle\sum_{i=1}^{n}\bar{x}^2\\&=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i^2-2\bar{x}^2+\bar{x}^2=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i^2-\bar{x}^2\end{aligned}\)

若采用分层随机抽样，分 \(n\) 层，样本数 \(m_1,m_2,\dots,m_n\)，平均值 \(x_1,x_2,\dots,x_n\)，\(\\\) 则样本平均数 \(\bar{x}=\displaystyle\sum_{i=1}^{n}\frac{m_i\cdot x_i}{\displaystyle\sum_{j=1}^{n}m_j}\)，注意样本平均数 \(\neq\) 总体平均数。

分层随机抽样需按比例分配：\(\frac{总体中第\ m\ 层个体数}{总体中第\ n\ 层个体数}=\frac{样本中第\ m\ 层个体数}{样本中第\ n\ 层个体数}\) 且 \(\frac{样本中第\ m\ 层个体数}{总体中第\ m\ 层个体数}=\frac{样本容量}{总体容量}\)

第 \(p\) 百分位数：数据中至少有 \(p\%\) 的数据 \(\leq\) 这个值，至少有 \((100-p)\%\) 的数 \(\geq\) 这个值。

第 \(25\) 百分位数：第一四分位数 / 下四分位数；第 \(75\) 百分位数：第三四分位数 / 上四分位数；第 \(50\) 百分位数：中位数。

已知数据求第 \(p\) 百分位数：1. 从小到大排序，令 \(i=n\times p\%\) 2. \(\begin{cases}\text{ans}=\frac{a_i+a_{i+1}}{2} & \lfloor i \rfloor = i \\ \text{ans}=a_{\lceil i \rceil} & \lfloor i \rfloor \neq i \end{cases}\)

格式要求：\(\begin{cases}[a,b) 的频率 <x\% \\ [a,c)的频率>x\%\end{cases}\implies\) 第 \(x\) 百分位数在 \([b,c)\) 内。

\(n\) 层构成样本的方差：\(s^2=\displaystyle\sum_{i=1}^{n}w_i[s_i^2+(\bar{x}_i-\bar{x})^2]\)，其中 \(\bar{x}_i\) 为样本中不同层的平均数，\(s_i^2\) 为不同层的方差，\(w_i\) 为相应的权重（ 该层样本数占总样本的多少，\(w_i<1\) ）。

特别地，只有 \(2\) 层时，若：

第 \(1\) 层	\(m\) 个数	\(\bar x\)	\(s^2\)
第 \(2\) 层	\(n\) 个数	\(\bar y\)	\(t^2\)

则总平均数 \(\displaystyle\bar a=\frac{m\bar x+n\bar y}{m+n}\)，总方差 \(\displaystyle b^2=\frac{ms^2+nt^2+m(\bar x-\bar a)^2+n(\bar y-\bar a)^2}{m+n}\)

若数据 \(x_1,x_2,\dots,x_n\) 的平均数 \(\bar x\)，方差 \(s^2\)，标准差 \(s\)，则数据 \(mx_1+a,mx_2+a,\dots,mx_n+a\) 的平均数 \(m\bar{x}+a\)，方差 \(s^2m^2\)，标准差 \(sm\)。

线性回归问题的一般步骤：

1. 列表 + 画散点图

   \(x\)	\(x_1\)	\(x_2\)	\(\dots\)	\(x_n\)
   \(y\)	\(y_1\)	\(y_2\)	\(\dots\)	\(y_n\)

2. 通过公式求 \(\hat b,\hat a\)。

\[\hat b=\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)}{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)^2}=\frac{\displaystyle\sum_{i=1}^{n} x_iy_i-n\bar x\bar y}{\displaystyle\sum_{i=1}^{n}x_i^2-n\bar x^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \hat a=\bar y-\hat b\bar x \]

3. 根据直线方程一定过 \(\bar x,\bar y\) 得出 \(\hat y=\hat bx+\hat a\)。

如果散点均匀分布在回归直线的两侧，那么回归效果就好

如果 \(\hat b > 0\) 则两变量正相关，反之则负相关，也可利用样本相关系数 \(r\) 来判断。

\(-1\leq r\leq 1,|r|\) 越接近 \(1\)，回归效果越好；\(r>0\) 则正相关，\(r<0\) 则负相关。

\[r=\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)}{\sqrt{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)^2\sum_{i=1}^{n}(y_i-\bar y)^2}}=\frac{\displaystyle\sum_{i=1}^{n} x_iy_i-n\bar x\bar y}{\sqrt{\displaystyle\sum_{i=1}^{n}x_i^2-n\bar x^2}\sqrt{\displaystyle\sum_{i=1}^{n}y_i^2-n\bar y^2}} \]

非线性回归方程：转化为线性回归方程。

1. 幂函数型：\(y=c_1x^{n}+c_2\ (n\) 一般为 \(\frac{1}{2}\) 或 \(2)\)。

   变换：令 \(t=x^n,b=c_1,a=c_2\)，则 \(y=bt+a\)。

2. 指数型：\(y=c_1e^{c_2x}\)。

   变换：两边取对数并令 \(z=\ln y,a=\ln c_1,b=c_2\)，则 \(z=bx+a\)。

变换后，需转化原函数关系，一般用相关指数来看拟合效果的强弱。（ 注：非线性的不能用相关系数 \(r\) ）

概率

基本概念

• 随机试验：对随机现象的实现和观察，用 \(E\) 表示。

• 样本点：\(E\) 的每个可能的基本结果，用 \(\omega\) 表示。

• 样本空间：全体 \(\omega\) 的集合，用 \(\Omega\) 表示。

• 有限样本空间：若一个随机试验有 \(n\) 个可能结果 \(\omega_1,\omega_2,\dots,\omega_n\)，则称样本空间 \(\Omega=\set{\omega_1,\omega_2,\dots,\omega_n}\) 为有限样本空间 \(\\\)（ 即 \(\Omega\) 为有限集 ）。

• 随机事件：\(\Omega\) 的子集，简称事件，用大写字母 \(A,B,C,\dots\) 表示，当且仅当 \(A\) 中的某个样本点出现时，称事件 \(A\) 发生。

• 基本事件：只包含一个样本点的事件。

• 必然事件：\(\Omega\) 作为自身的子集，包含了所有样本点，在每次试验中总有一个样本点发生，即 \(\Omega\) 总会发生。

• 不可能事件：\(\varnothing\) 不含任何样本点，在每次试验中都不会发生，必然事件与不可能事件不具有随机性。

事件的关系和运算

事件的关系	含义	符号表示
包含	\(A\) 发生 \(\implies B\) 发生	\(A\subseteq B\)
并事件 / 和事件	\(A\) 和 \(B\) 至少一个发生	\(A\bigcup B\) 或 \(A+B\)
交事件 / 积事件	\(A\) 和 \(B\) 同时发生	\(A\bigcap B\) 或 \(AB\)
互斥 / 互不相容	\(A\) 和 \(B\) 不能同时发生	\(A\bigcap B=\varnothing\)
互为独立	\(A\) 和 \(B\) 有且仅有一个发生	\(A\bigcap B=\varnothing\) 且 \(A\bigcup B=\Omega\)

如果 \(A,B\) 互斥，记 \(\bar{A},\bar{B}\) 分别为 \(A,B\) 的对立事件。

若 \(A\subseteq B\) 且 \(B\subseteq A\)，则事件 \(A\) 和事件 \(B\) 相等，\(A=B\)。

对于三个事件 \(A,B,C\)，\(A\bigcup B\bigcup C\) 或 \(A+B+C\) 表示 \(A,B,C\) 至少一个发生，其余同理。

古典概型

• 满足有限性（ 有限样本空间 ）、等可能性。

• 设 \(E\) 为古典概型，样本空间 \(\Omega\) 包含 \(n\) 个样本点，事件 \(A\) 包含其中的 \(k\) 个样本点，则事件 \(A\) 的概率为 \(P(A)=\frac{k}{n}=\frac{n(A)}{n(\Omega)} \\ n(A),n(\Omega)\) 表示事件 \(A\) 和样本空间 \(\Omega\) 包含的样本点个数。

概率的基本性质

1. \(\forall A,0\leq P(A)\leq 1\)
2. 必然事件 \(\Omega\) 概率为 \(P(\Omega)=1\)，不可能事件 \(\varnothing\) 概率为 \(P(\varnothing)=0\)。
3. 若 \(A,B\) 互斥，则 \(P(A\bigcup B)=P(A)+P(B)\)； \(\\\) 推广：若 \(A_1,A_2,\dots,A_m\) 两两互斥，则 \(P(A_1\bigcup A_2\bigcup\dots\bigcup A_m)=\displaystyle\sum_{i=1}^{m}P(A_i)\)
4. 若 \(A,B\) 对立，则 \(P(B)=1-P(A),P(A)=1-P(B)\)；若 \(P(A)+P(B)=1\)，则 \(A,B\) 不一定对立。
5. 若 \(A\subseteq B\)，则 \(P(A)\leq P(B)\)（ 概率的单调性 ）。
6. 设 \(A,B\) 为随机试验中的两个事件，则 \(P(A\bigcup B)=P(A)+P(B)-P(A\bigcap B)\) （ 容斥原理 ）。
7. 对任意 \(2\) 个事件 \(A,B\)，若 \(P(AB)=P(A)P(B)\)，则 \(A\) 与 \(B\) 相互独立，记 \(A,B\) 的对立事件分别为 \(\bar{A},\bar{B}\) \(\\\) 因事件 \(A,B\) 的发生互不影响，则 \(A\) 与 \(\bar{B}\)，\(\bar{A}\) 与 \(B\)，\(\bar{A}\) 与 \(\bar{B}\) 也相互独立。
8. 若 \(A,B,C\) 两两独立，则 \(P(ABC)\neq P(A)P(B)P(C)\)。
9. \(\bar{A}\cap\bar{B}=\overline{A\cup B},\bar{A}\cup\bar{B}=\overline{A\cap B}\)

事件含义	事件表示	概率	\(A,B\) 互斥	\(A,B\) 相互独立
\(A\) 和 \(B\) 至少一个发生	\(A\bigcup B\)	\(P(A\bigcup B)\)	\(P(A)+P(B)\)	\(1-P(\bar{A})P(\bar{B})\)
\(A\) 和 \(B\) 同时发生	\(AB\)	\(P(AB)\)	\(0\)	\(P(A)P(B)\)
\(A\) 和 \(B\) 都不发生	\(\bar{A}\bar{B}\)	\(P(\bar{A}\bar{B})\)	\(1-[P(A)+P(B)]\)	\(P(\bar{A})P(\bar{B})\)
\(A\) 和 \(B\) 只有一个发生	\(A\bar{B}+\bar{A}B\)	\(P(A\bar{B}\bigcup\bar{A}B)\)	\(P(A)+P(B)\)	\(P(A)P(\bar{B})+P(\bar{A})P(B)\)

平面几何

Menelaus 梅涅劳斯定理

\[\frac{AF}{FB}\frac{BD}{DC}\frac{CE}{EA}=1 \]

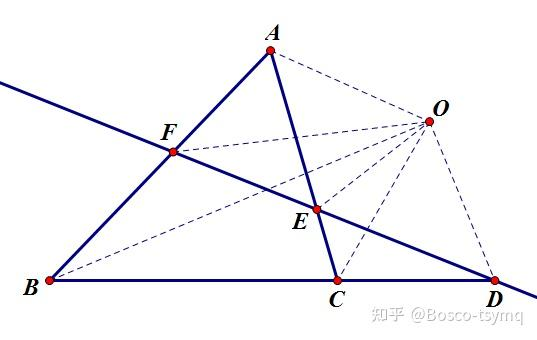
第一角元形式：\(\frac{\sin\angle ACF}{\sin\angle FCB}\frac{\sin\angle BAD}{\sin\angle DAC}\frac{\sin\angle CBE}{\sin\angle EBA}=1\)

第二角元形式：\(\frac{\sin\angle AOF}{\sin\angle FOB}\frac{\sin\angle BOD}{\sin\angle DOC}\frac{\sin\angle COE}{\sin\angle EOA}=1\)

Ceva 塞瓦定理

\[\frac{AF}{FB}\frac{BD}{DC}\frac{CE}{EA}=1 \]

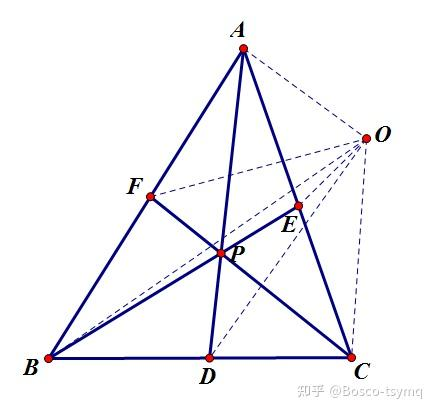
第一角元形式：\(\frac{\sin\angle ACF}{\sin\angle FCB}\frac{\sin\angle BAD}{\sin\angle DAC}\frac{\sin\angle CBE}{\sin\angle EBA}=1\)

第二角元形式：\(\frac{\sin\angle AOF}{\sin\angle FOB}\frac{\sin\angle BOD}{\sin\angle DOC}\frac{\sin\angle COE}{\sin\angle EOA}=1\)

Stewart 定理

\[AD^2=\frac{AC^2\cdot BD+AB^2\cdot DC}{BC}-BD\cdot DC \]

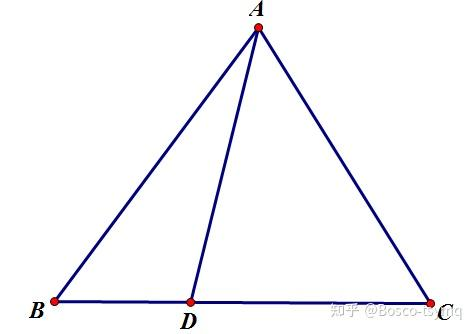
中线长公式：\(m_a^2=\frac{1}{2}AB^2+\frac{1}{2}AC^2-\frac{1}{4}BC^2\)

角平分线长公式：\(t_a=AB\cdot AC-BD\cdot DC=\frac{2}{AB+AC}\sqrt{AB\cdot AC\cdot p\cdot(p-BC)},p=\frac{AB+BC+CA}{2}\)

调和点列

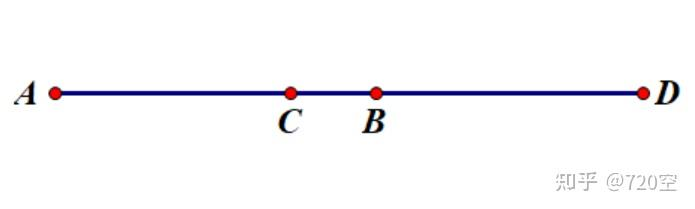
定义：若 \(\displaystyle\frac{AC}{CB}=\frac{AD}{DB}\)，则称 \((A,B,C,D)\) 为调和点列，\(C,D\) 调和分割线段 \(A,B\)。

性质：以下设 \(M\) 为 \(AB\) 中点。

1. \(\frac{1}{AC}+\frac{1}{AD}=\frac{2}{AB}\)，即 \(AB\) 的长度是 \(AC\) 和 \(AD\) 长度的调和平均值。
2. \(AB\cdot CD=2AD\cdot BC=2AC\cdot DB\)
3. \(CA\cdot CB=CM\cdot CD\)，\(DA\cdot DB=DM\cdot DC\)
4. \(MA^2=MB^2=MC\cdot MD\)

内切圆和调和点列

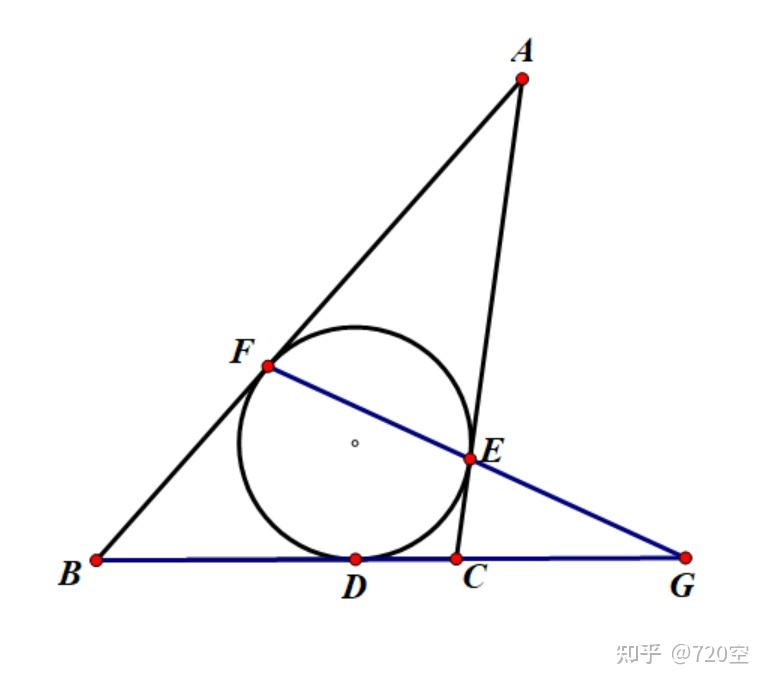
由梅涅劳斯定理得 \(\frac{AF}{FB}\frac{BG}{GC}\frac{CE}{EA}=1\)，又因为 \(AF=AE,BF=BD,CE=CD\)，

得 \(\frac{BD}{CD}=\frac{BG}{CG}\implies(B,D,C,G)\) 为调和点列。

极线和调和点列

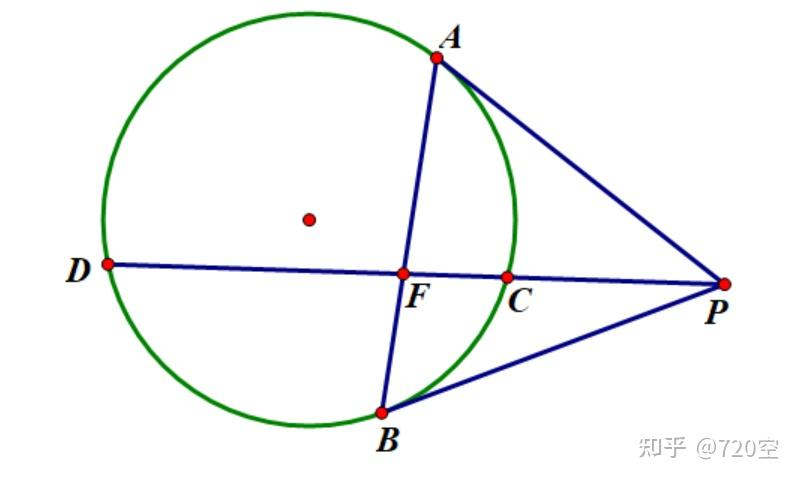
\(PA,PB\) 为两条切线，\(P\) 是极点，\(AB\) 是极线，则 \(\frac{CP}{DP}=\frac{CF}{DF},(P,C,F,D)\) 是调和点列。

线性规划

例题 1

\[\begin{cases}5x-11y \geq -22 \\ 2x+3y \geq 9 \\ 2x \leq 11\end{cases} \]

\(z = 10x + 10y, \max{z} = \ ?\)

基本概念

1. 约束条件：变量 \(x,y,\dots\) 满足的一组条件，上述二元一次不等式组就是对 \(x,y\) 的约束条件。
2. 线性约束条件：由变量 \(x,y,\dots\) 的一次不等式 / 方程组成的不等式组就称为线性约束条件，如上述二元一次不等式。
3. 目标函数：欲求最大值或最小值所涉及的变量 \(x,y,\dots\) 的解析式，如上述 \(z\)。
4. 线性目标函数：目标函数关于变量 \(x,y,\dots\) 的一次解析式，如上述 \(z\)。
5. 线性规划问题：在线性约束条件下求线性目标函数的问题。
6. 可行解：满足线性约束条件的解 \((x,y)\)。
7. 可行域：由所有可行解组成的集合。
8. 最优解：使目标函数取得 \(\max\) 或 \(\min\) 的可行解。

解法

1. 画图，数形结合。

   \[\begin{cases}5x-11y \geq -22 & \implies y \leq \frac{5}{11}x + \frac{1}{2} & \implies & y = \frac{5}{11}x + \frac{1}{2}\ 图像的下边 \\ 2x+3y \geq 9 & \implies y \geq -\frac{2}{3}x + 3 & \implies & y = -\frac{2}{3}x + 3\ 图像的上边 \\ 2x \leq 11 & \implies x \leq \frac{11}{2} & \implies & x=\frac{11}{2}\ 图像的左边 \end{cases} \]

   在平面直角坐标系上画出对应的平面区域 （ 可行域 ），再把目标函数 \(z=ax+by\) 变形为 \(y=-\frac{a}{b}x + \frac{z}{b}\)，\(\\\) 所以求 \(z\) 的最值可看成是求直线 \(y=-\frac{a}{b}x + \frac{z}{b}\) 在 \(y\) 轴上截距的最值。以这题为例，\(\\ z=10x+10y \implies y= -x + \frac{z}{10}\) 容易证明，当 \(z=85\) 时 \(y\) 轴上截距取最值，所以 \(\max{z}=85.\)

   

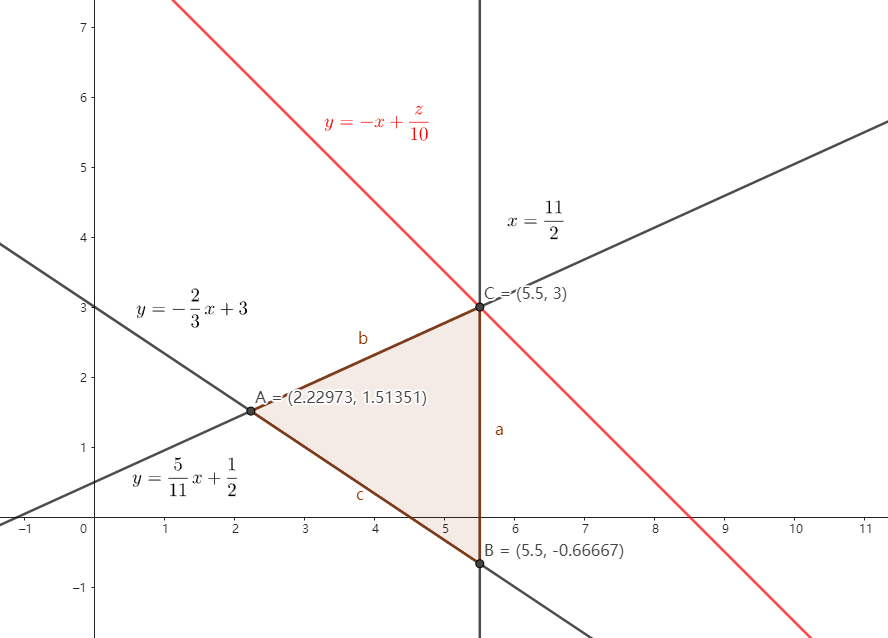
2. 仔细观察，可以发现最优解非常容易出现在可行域构成的多面体的顶点处。

例题 2

\[\begin{cases}y \geq x \\ x + y \leq 2 \\ x \geq a\end{cases} \]

\((2x+y)_{\mathrm{max}}=4(2x+y)_{\mathrm{min}},\ a=\ ?\)

• 求 \((2x+y)_{\mathrm{min}}\)：\(x_{\min}=a \implies y_{\min}=a \implies (2x+y)_{\mathrm{min}}=3a\)

• 求 \((2x+y)_{\mathrm{max}}\)：\(\begin{cases}x-y\leq 0 \\ x+y\leq 2\end{cases}\xRightarrow{\mathrm{Add\ }} x\leq 1\implies y\leq 1\implies (2x+y)_{\mathrm{max}}=3\)

• \(3=4\times 3a\implies a=\frac{1}{4}\)

例题 3（ 2024 九省联考 T14 ）

\[\begin{cases} 0<a<b<c<1 \\ b\geq 2a \ \ \ \mathrm{or}\ \ \ a+b\leq 1 \end{cases} \]

\(\max{\set{b-a,c-b,1-c}}\) 的最小值 \(=\ ?\)

• 注意到 \(c\) 的约束条件是最少的，首先考虑消去它，得到

\[\max{\set{b-a,c-b,1-c}}\geq\max{\set{b-a,\frac{1-b}{2}}} \]

\(\ \ \ \ \ \ \text{}\) 当且仅当 \(c=\frac{1+b}{2}\) 取等，消去 \(c\) 后把 \(a\) 看作 \(x\)，把 \(b\) 看作 \(y\) 得：

\[\begin{cases}0<x \\ x<y \\ y<1 \\ y\geq 2x\ \ \ \mathrm{or}\ \ \ x+y\leq 1\end{cases} \]

• 作出可行域：\(\mathrm{and}\) 连接的区域之间取交，\(\mathrm{or}\) 连接的区域之间取并。阴影部分即为可行域。

\(\ \ \ \ \ \ \text{}\) 图中 \(y\geq 2x\ \ \ x+y\leq 1\) 两条解析式用红色标出。

• 回到题目，要求 \(M=\max{\set{y-x,\frac{1-y}{2}}}\)，我们需要知道何时 \(M=y-x\)，何时 \(M=\frac{1-y}{2}\)

\(\ \ \ \ \ \ \text{}\) 直接列方程 \(y-x=\frac{1-y}{2}\) 可以得到 \(y=\frac{2}{3}x+\frac{1}{3}\)，在图中作出这条直线，得到：

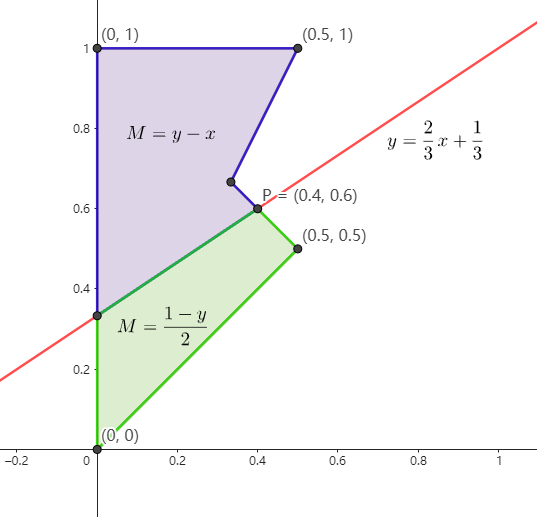
• 因为最终要求的是 \(M\) 的最小值，所以对蓝色区域而言，\(y\) 尽量小，\(x\) 尽量大，根据例题 1 的经验，这样的极值点通常出现在多边形的顶点处，经过比较后 \(P\) 点是极值点，此时 \(M=0.2\)。对绿色区域而言，只需满足 \(y\) 尽量大，显然，\(P\) 点也是极值点。
• 综上所述，\(\max{\set{b-a,c-b,1-c}}\) 的最小值 \(=\frac{1}{5}\)。

数论

因为这里是数学笔记，不是 OI 笔记，因此只有一些简要的定理。

质数

• 定义：一个正整数无法被除了 \(1\) 和它自身之外的任何自然数整除，则成为质数，否则为合数。

• 数量：对于一个足够大的整数 \(N\)，不超过 \(N\) 的质数有 \(\pi(x)\approx\frac{N}{\ln N}\) 个，所以第 \(n\) 个质数约为 \(n\ln n\)。

• 判定：试除法，若 \(N\) 为合数，则存在一个能整除 \(N\) 的数 \(T\) 且 \(2 \leq T \leq \sqrt{N}\)。

• 算数基本定理：\(N = p_1^{c_1}p_2^{c_2}\dots p_n^{c_n}\)，\(N\) 的正约数个数 \(=\displaystyle\prod_{i=1}^{n}(c_i+1)\)，

  \(N\) 的所有正约数的和 \(=\displaystyle\prod_{i=1}^{n}(\displaystyle\sum_{j=0}^{c_i}(p_i)^j)\)。

  一个正整数 \(N\) 的约数个数上界为 \(2\sqrt{N}\)，\(1\) ~ \(N\) 每个数的约数个数的总和大约为 \(N\log N\)。

因数

整除

若 \(b\) 能整除 \(a\)，则记为 \(a\mid b\)，如 \(2\mid 12\)。若 \(b\) 不能整除 \(a\)，则记为 \(a\nmid b\)，如 \(5\nmid 12\)。

若 \(a\nmid b\)，则 \(b\div a\) 存在余数 \(r\) 且 \(0<r<a\)，记 \(r=a\ \mathrm{mod}\ b\)。例如，\(3\ \mathrm{mod}\ 2=1\)。

整除具有以下性质：

1. 若 \(a\mid b\) 且 \(a\mid c\)，则 \(\forall x,y\)，有 \(a\mid xb+yc\)。
2. 若 \(a\mid b\) 且 \(b\mid c\)，则 \(a\mid c\)。
3. 若 \(a\mid b\) 且 \(b\mid a\)，则 \(a=\pm b\)。
4. 设 \(m\neq 0\)，则 \(a\mid b\)，当且仅当 \(ma\mid mb\)。

最大公因数与最小公倍数

设 \(a,b\) 是两个不为 \(0\) 的整数，能使 \(d\mid a\) 和 \(d\mid b\) 成立的最大整数 \(d\)，称为 \(a,b\) 的最大公因数，记作 \(\gcd(a,b)\)。

设 \(a,b\) 是两个不为 \(0\) 的整数，能使 \(a\mid d\) 和 \(b\mid d\) 成立的最小整数 \(d\)，称为 \(a,b\) 的最小公倍数，记作 \(\mathrm{lcm}(a,b)\)。

• \(\forall a,b\in\N,\ \gcd(a,b)\cdot\mathrm{lcm}(a,b)=ab\)

证明：设 \(d=\gcd(a,b),a_0=\frac{a}{d},b_0=\frac{b}{d}\)。根据最大公因数的定义，有 \(\gcd(a_0,b_0)=1\)。\(\\\ \ \ \ \ \ \ \ \ \text{}\) 再根据最小公倍数的定义，有 \(\mathrm{lcm}(a,b)=a_0\cdot b_0\)。\(\\\ \ \ \ \ \ \ \ \ \text{}\) 于是 \(\mathrm{lcm}(a,b)=\mathrm{lcm}(a_0\cdot d,b_0\cdot d)=\mathrm{lcm}(a_0,b_0)\cdot d=a_0\cdot b_0\cdot d=\frac{a\cdot b}{d}\)，原命题得证。

• 九章算术 更相减损术： \(\gcd(a,b)=\gcd(b,a-b)=\gcd(a,a-b),\gcd(2a,2b)=2\gcd(a,b)\)。

证明：\(d\mid a,d\mid b\implies d\mid(a-b)\)。

• 欧几里得算法：\(\forall a,b\in\N,b\neq 0,\gcd(a,b)=\gcd(b,a\ \mathrm{mod}\ b)\)。

证明：分类讨论。

1. 若 \(a<b\)，则有 \(\gcd(b,a\ \mathrm{mod}\ b)=\gcd(b,a)=\gcd(a,b)\)。
2. 若 \(a\geq b\)，不妨设 \(a=q\cdot b+r\ (0\leq r<b)\)。显然 \(r=a\ \mathrm{mod}\ b\)。对于 \(a,b\) 的任意公因数 \(d\)，\(\\\) 因为 \(d\mid a,d\mid q\cdot b\)，故 \(d\mid (a-q\cdot b)\)，即 \(d\mid r\)。因此 \(d\) 也是 \(b,r\) 的公因数，反之亦成立。\(\\\) 故 \(a,b\) 的公因数集合与 \(b,a\ \mathrm{mod}\ b\) 的公因数集合相同。于是它们的最大公因数也相等。

欧拉函数

\(1\) ~ \(N\) 中与 \(N\) 互质的数的个数被称为欧拉函数，记为 \(\varphi(N)\)。用数学符号表示即为 \(\varphi(N)=\displaystyle\sum_{i=1}^{N}[\gcd(i,N)=1]\)。

若 \(N = p_1^{c_1}p_2^{c_2}\dots p_n^{c_n}\)，则 \(\varphi(N)=N\times\frac{p_1-1}{p_1}\times\frac{p_2-1}{p_2}\times\dots\times\frac{p_n-1}{p_n}=N\cdot\displaystyle\prod_{质数p|N}(1-\frac{1}{p})\)

证明：设 \(p,q\) 为 \(N\) 的不同质因子，\(1\) ~ \(N\) 中 \(p\) 的倍数有 \(N\over p\) 个，\(q\) 的倍数有 \(N \over q\) 个。若把 \(\frac{N}{p}+\frac{N}{q}\) 个数去掉，则 \(\frac{N}{pq}\) 被计算了 \(2\) 次（ 容斥原理 ）。因此， \(1\) ~ \(N\) 中不与 \(N\) 含有相同质因子的 \(p\) 或 \(q\) 数量为 \(\\ N-\frac{N}{p}-\frac{N}{q}+\frac{N}{pq}=N(1-\frac{1}{p})(1-\frac{1}{q})\)，对 \(N\) 的全部质因子继续容斥即可得到公式。

\(n\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)	\(13\)	\(14\)	\(15\)
\(\varphi(n)\)	\(1\)	\(1\)	\(2\)	\(2\)	\(4\)	\(2\)	\(6\)	\(4\)	\(6\)	\(4\)	\(10\)	\(4\)	\(12\)	\(6\)	\(8\)

欧拉函数的性质：

1. \(\forall n>1\)，\(1\) ~ \(n\) 中与 \(n\) 互质的数的和为 \(\frac{n\times\varphi(n)}{2}\)。
2. 若 \(a,b\) 互质，则 \(\varphi(ab)=\varphi(a)\varphi(b)\)。
3. 设 \(p\) 为质数，\(\varphi(p)=p-1\)。
4. 设 \(p\) 为质数，\(k\in\N^*,\varphi(p^k)=p^{k-1}\times(p-1)=p^k-p^{k-1}\)。
5. 设 \(p\) 为质数，若 \(p\mid n\) 且 \(p^2\mid n\)，则 \(\varphi(n)=\varphi(\frac{n}{p})\times p\)。
6. 设 \(p\) 为质数，若 \(p\mid n\) 但 \(p^2\nmid n\)，则 \(\varphi(n)=\varphi(\frac{n}{p})\times (p-1)\)。
7. 若 \(n\) 为奇数，则 \(\varphi(2n)=\varphi(n)\)。
8. \(\forall n\geq 3,\ n\in\N^*,\ 2\mid\varphi(n)\)。
9. 欧拉反演：\(\displaystyle\sum_{d\mid n}\varphi(d)=n\)。

证明：

1. 因为 \(\gcd(n,x)=\gcd(n,n-x)\)，所以与 \(n\) 不互质的数 \(x,n-x\) 成对出现，平均值为 \(\frac{n}{2}\)。\(\\\) 因此与 \(n\) 互质的数的平均值也是 \(\frac{n}{2}\)，进而得到性质 1。
2. 根据欧拉函数的计算式可直接获得性质 2。
3. 根据欧拉函数的定义可直接获得性质 3。
4. 从 \(1\) ~ \(p^{k}\) 中的所有数，除了 \(p^{k-1}\) 个 \(p\) 的倍数外都与 \(p^k\) 互素。
5. 若 \(p\mid n\) 且 \(p^2\mid n\)，则 \(n,\frac{n}{p}\) 包含相同的质因子，只是 \(p\) 的指数不同。\(\\\) 按照欧拉函数的计算公式，\(\frac{\varphi(n)}{\varphi(\frac{n}{p})}=\frac{n}{\frac{n}{p}}=p\)，得到性质 5。
6. 若 \(p\mid n\) 且 \(p^2\mid n\)，则 \(n,\frac{n}{p}\) 互质。因为 \(\varphi(n)=\varphi(\frac{n}{p})\varphi(p)\)，而 \(\varphi(p)=p-1\)，得到性质 6。
7. \(\forall m<2n,m\in\N^*\)，若 \(2\mid m\)，则 \(\gcd(m,2n)\neq 1\)，也就是对欧拉函数的值没有贡献；\(\\\)若 \(2\nmid m\)，则 \(\gcd(m,2n)=1\)，欧拉函数的值也就与 \(2n\) 中的偶质因子无关。
8. \(n\geq 3\) 时，与 \(n\) 互质的数不可能为 \(\frac{n}{2}\implies\forall x<n,\gcd(x,n)=\gcd(n-x,n)\)，也就是存在一一对应关系。
9. 设 \(f(n)=\displaystyle\sum_{d\mid n}\varphi(d)\)，利用 \(\varphi\) 是积性函数，得到：\(\\\)若 \(n,m\) 互质，则 \(f(nm)=\displaystyle\sum_{d\mid nm}\varphi(d)=\displaystyle\sum_{d\mid n}\varphi(d)\cdot\displaystyle\sum_{d\mid m}\varphi(d)=f(n)f(m)\)，即 \(f(n)\) 是积性函数。\(\\\) 对于单个质因子有：\(\begin{aligned}f(p^m)&=\displaystyle\sum_{d\mid p^m}\varphi(d)=\displaystyle\sum_{i=0}^{m}\varphi(p^i)=\varphi(1)+\varphi(p)+\varphi(p^2)+\varphi(p^3)+\dots+\varphi(p^m)\\&= 1+(p-1)+(p-1)p+(p-1)p^2+\dots+(p-1)p^{m-1}\\&=1+(p-1)+(p^2-p)+(p^3-p^2)+\dots+(p^m-p^{m-1})=p^m\end{aligned} \\\) 所以 \(f(n)=\displaystyle\prod_{i=1}^{m}f(p_i^{c_i})=\displaystyle\prod_{i=1}^{m}p_i^{c_i}=n\)

积性函数与完全积性函数

若函数 \(f(x)\) 满足 \(f(1)=1\) 且 \(\forall x,y\in\N^{*},\gcd(x,y)=1\) 都有 \(f(xy)=f(x)f(y)\)，则 \(f(x)\) 是积性函数。

若函数 \(f(x)\) 满足 \(f(1)=1\) 且 \(\forall x,y\in\N^{*}\) 都有 \(f(xy)=f(x)f(y)\)，则 \(f(x)\) 是完全积性函数。

性质：

1. 若 \(f(x)\) 和 \(g(x)\) 均为积性函数，则以下函数也为积性函数：

   \[\begin{aligned}h(x)&=f(x^p) \\ h(x)&=f^p(x) \\ h(x)&=f(x)g(x) \\ h(x)&=\displaystyle\sum_{d\mid x}f(d)g(\frac{x}{d})\end{aligned} \]

2. 设 \(x=\displaystyle\prod p_i^{c_i}\)，

   若 \(f(x)\) 为积性函数，则 \(f(x)=\displaystyle\prod f(p_i^{c_i})\)。

   若 \(f(x)\) 为完全积性函数，则 \(f(x)=\displaystyle\prod f^{c_i}(p_i)\)。

例子：

积性函数：\(\varphi(n),\sigma _k(n)=\displaystyle\sum_{d\mid n}d^k,\sigma _0(n)\) 通常简记为 \(d(n)\) 或 \(\tau(n)\)，\(\sigma _1(n)\) 通常简记为 \(\sigma(n)\)。

完全积性函数：\(\varepsilon(n)=[n=1],\text{id}_k(n)=n^k,\text{id}_1(n)\) 通常简记为 \(\text{id}(n),f(n)=1\)。

同余

费马小定理与欧拉定理

若整数 \(a\) 和整数 \(b\) 除以正整数 \(m\) 的余数相等，则称 \(a,b\) 模 \(m\) 同余，记为 \(a\equiv b\ (\mathrm{mod}\ m)\)。

并且注意到 \(k\ \mathrm{mod}\ i=k-\lfloor\frac{k}{i}\rfloor\cdot i\)，且同余满足同加性、同乘性、同幂性，但不满足同除性。

对于 \(\forall a \in [0, m - 1]\)，集合 \(\set{a+km\ (k\in\Z)}\) 的所有数模 \(m\) 同余，余数都是 \(a\)。该集合称为一个模 \(m\) 的同余类，简记为 \(\overline{a}\)。

模 \(m\) 的同余类一共有 \(m\) 个，分别为 \(\overline{0},\overline{1},\overline{2},\dots,\overline{m-1}\)。它们构成 \(m\) 的完全剩余系。

\(1\) ~ \(m\) 中与 \(m\) 互质的数代表的同余类共有 \(\varphi(m)\) 个，它们构成 \(m\) 的简化剩余系。\(\\\)例如，模 \(10\) 的简化剩余系为 \(\set{\overline{1},\overline{3},\overline{7},\overline{9}}\)。

若从某个非空数集中任选两个元素（ 同一元素可重复选出 ），选出的这两个元素通过某种（ 或几种 ）运算后的得数仍是该数集中的元素，那么，就说该集合对于这种（ 或几种 ）运算是封闭的。\(\\\)例如若一个集合中的元素，如果能够做到做加法运算的结果还在这个集合中，就说这个集合对加法运算封闭。\(\\\) 例如 \(\N\) 对加法、乘法运算是封闭的；\(\Z\) 对加、减、乘法运算是封闭的；\(\mathbb{Q}, \mathbb{C}\) 对四则运算是封闭的。

简化剩余系关于模 \(m\) 乘法封闭。这是因为若 \(a,b\ (1\leq a,b\leq m)\) 与 \(m\) 互质，则 \(ab\) 也与 \(m\) 互质。\(\\\)由余数的定义得 \(ab\ \mathrm{mod}\ m\) 也与 \(m\) 互质，即 \(ab\ \mathrm{mod}\ m\) 也属于 \(m\) 的简化剩余系。

• 费马小定理：若 \(p\) 是质数，则对于任意整数 \(a\)，有 \(a^p\equiv a\ (\mathrm{mod}\ p)\)。
• 欧拉定理：若正整数 \(a,n\) 互质，则 \(a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)\)。

证明：设 \(n\) 的简化剩余系为 \(\set{\overline{a_1},\overline{a_2},\dots,\overline{a_{\varphi(n)}}}\)。\(\forall a_i,a_j\)，若 \(a\cdot a_i\equiv a\cdot a_j\ (\mathrm{mod}\ n)\)，则 \(a\cdot(a_i-a_j)\equiv 0\\\) 因为 \(a,n\) 互质，所以 \(a_i\equiv a_j\)。故当 \(a_i\neq a_j\) 时，\(aa_i,aa_j\) 也代表不同的同余类。

又因为简化剩余系关于模 \(m\) 乘法封闭，故 \(\overline{aa_1}\) 也在简化剩余系集合中。因此，集合 \(\set{\overline{a_1},\overline{a_2},\dots,\overline{a_{\varphi(n)}}}\) 与集合 \(\set{\overline{aa_1},\overline{aa_2},\dots,\overline{aa_{\varphi(n)}}}\) 都能表示 \(n\) 的简化剩余系。综上所述：

\[a^{\varphi(n)}a_1a_2\dots a_{\varphi(n)}\equiv(aa_1)(aa_2)\dots(aa_{\varphi(n)})\equiv a_1a_2\dots a_{\varphi(n)}\ (\mathrm{mod}\ n) \]

因此 \(a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)\)。当 \(p\) 为质数时，满足 \(\varphi(p)=p-1\)，两边同乘 \(a\) 即可得到费马小定理。

另外，当 \(a\) 是 \(p\) 的倍数，费马小定理显然成立。

---

• 欧拉定理的推论：若正整数 \(a,n\) 互质，则对于任意正整数 \(b\)，有 \(a^b\equiv a^{b\ \mathrm{mod}\ \varphi(n)}\ (\mathrm{mod}\ n)\)

证明：设 \(b=q\cdot \varphi(n)+r\)，其中 \(0\leq r<\varphi(n)\)，即 \(r=b\ \mathrm{mod}\ \varphi(n)\)。于是有：

\[a^b\equiv a^{q\cdot\varphi(n)+r}\equiv (a^{\varphi(n)})^q\cdot a^r\equiv 1^q\cdot a^r\equiv a^r\equiv a^{b\ \mathrm{mod}\ \varphi(n)}\ (\mathrm{mod}\ n) \]

证毕。面对 \(a+b,a-b,a\cdot b\) 这样的算式，可以在计算前先把 \(a,b\) 对 \(p\) 取模。面对 \(a^b\) 这样的乘方算式，可以先把底数对 \(p\) 取模、指数对 \(\varphi(p)\) 取模，再计算乘方。

即 \(a^b\equiv (a\ \mathrm{mod}\ p)^{b\ \mathrm{mod}\ \varphi(p)}\ (\mathrm{mod}\ p)\)

---

• 扩展欧拉定理

  \[a^b\equiv\begin{cases}a^{b\ \mathrm{mod}\ \varphi(m)}&\text{if }\gcd(a,m)=1\\ a^b&\text{if }\gcd(a,m)\neq 1,b<\varphi(m)\\ a^{b\ \mathrm{mod}\ \varphi(m)+\varphi(m)}&\text{if }\gcd(a,m)\neq 1,b\geq\varphi(m)\end{cases}\ (\mathrm{mod}\ m) \]

  证明十分显然，略。

---

• 若正整数 \(a,n\) 互质，则满足 \(a^x\equiv 1\ (\mathrm{mod}\ n)\) 的最小正整数 \(x_0\) 是 \(\varphi(n)\) 的约数。

反证法，假设满足 \(a^x\equiv 1\ (\mathrm{mod}\ n)\) 的最小正整数 \(x_0\) 不能整除 \(\varphi(n)\)。

设 \(\varphi(n)=qx_0+r\ (0<r<x_0)\)，因为 \(a^{x_0}\equiv 1\ (\mathrm{mod}\ n)\)，所以 \(a^{qx_0}\equiv 1\ (\mathrm{mod}\ n)\)。根据欧拉定理 \(a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)\)，所以 \(a^r\equiv 1\ (\mathrm{mod}\ n)\)。这与 \(x_0\) 最小矛盾。故假设不成立，原命题成立。

中国剩余定理

设 \(m_1,m_2,\dots,m_n\) 是两两互质的整数，\(m=\displaystyle\prod_{i=1}^n m_i,M_i=\frac{m}{m_i},t_i\) 是线性同余方程 \(M_it_i\equiv 1\ (\mathrm{mod}\ m_i)\) 的一个解。对于任意的 \(n\) 个整数，方程组

\[\begin{cases}x\equiv a_1\ (\mathrm{mod}\ m_1) \\ x\equiv a_2\ (\mathrm{mod}\ m_2)\\ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ x\equiv a_n\ (\mathrm{mod}\ m_n)\end{cases} \]

有整数解，解为 \(x=\displaystyle\sum_{i=1}^{n}a_iM_it_i\)，通解可以表示为 \(x+km(k\in\Z)\)，最小非负整数解为 \(x\ \mathrm{mod}\ m\)。

证明：因为 \(M_i=\frac{m}{m_i}\) 是除了 \(m_i\) 之外所有模数的倍数，所以 \(\forall k\neq i,a_iM_it_i\equiv 0\ (\mathrm{mod}\ m_i)\)，\(\\ \ \ \ \ \ \ \ \ \ \ \text{}\)所以代入 \(x=\displaystyle\sum_{i=1}^{n}a_iM_it_i\)，原方程组成立。

威尔逊定理

• \(p\) 为素数 \(\xLeftrightarrow{}(p-1)!\equiv -1\ (\mathrm{mod}\ p)\)

证明：

1. 充分性

   对于 \(p\) 不是素数的情况，有 \(\begin{cases} p=1 & (1-1)!\equiv 0\ (\mathrm{mod}\ 1) \\ p=4 & (4-1)!\equiv 2\ (\mathrm{mod}\ 4) \\ p>4 & 分类讨论得出\ (p-1)!\equiv 0\ (\mathrm{mod}\ p) \end{cases}\)

   (a) 当 \(p\) 为完全平方数。

   则 \(p=k^2\) 且 \(k>2\)，用相减法比较 \(2k\) 与 \(p\) 的大小得 \(2k<p\)，于是有

   \[\begin{aligned}(p-1)!&=1\times 2\times\dots\times k\times\dots\times 2k\times\dots\times (p-1)\\ &=2nk^2\\&=2np\end{aligned} \]

   所以 \((p-1)!\equiv 0\ (\mathrm{mod}\ p)\) 且 \(p\) 为完全平方数。

   (b) 当 \(p\) 不为完全平方数。

   则 \(p\) 可以表示为两个不相等的数 \(a\) 和 \(b\) 的乘积，设 \(a<b\)，则有 \(p=ab,1<a<b<p\)

   \[\begin{aligned}(p-1)!&=1\times 2\times\dots\times a\times\dots\times b\times\dots\times (p-1)\\&=a\times b\times n\\ &=np\end{aligned} \]

   所以 \((p-1)!\equiv 0\ (\mathrm{mod}\ p)\) 且 \(p\) 不为完全平方数。

2. 必要性

   当 \(p\) 为素数时，考虑二次剩余式 \(x^2\equiv 1\ (\mathrm{mod}\ p)\)，化简得 \((x-1)(x+1)\equiv 0\ (\mathrm{mod}\ p)\)

   于是 \(x\equiv 1\ (\mathrm{mod}\ p)\) 或 \(x\equiv p-1\ (\mathrm{mod}\ p)\)。现在先抛开 \(1\) 和 \(p-1\) 不管，

   \(\forall a\in [2,p-2]\)，必然存在一个和它不相等的逆元 \(a^{-1}\in[2,p-2]\)，满足 \(aa^{-1}\equiv 1\ (\mathrm{mod}\ p)\)

   所以必然有 \(\frac{p-3}{2}\) 对数相乘的乘积为 \(1\)，即 \((p-2)!\equiv 1\ (\mathrm{mod}\ p)\)

   等式两边同时乘 \(p-1\) 就得到威尔逊定理。

例题：\(n\in\N^*\) 且 \(n\leq 10^6\)，求 \(S_n\)。

\[S_n=\displaystyle\sum_{k=1}^{n}\lfloor\frac{(3k+6)!+1}{3k+7}-\lfloor\frac{(3k+6)!}{3k+7}\rfloor\rfloor \]

令 \(d=3k+7\)，原式化简为

\[S_n=\displaystyle\sum_{k=1}^{n}\lfloor\frac{(d-1)!+1}{d}-\lfloor\frac{(d-1)!}{d}\rfloor\rfloor \]

由威尔逊定理，当 \(d\) 为素数时，\(\frac{(d-1)!+1}{d}\) 必然是整数，而 \(\lfloor\frac{(d-1)!}{d}\rfloor\) 必然比 \(\frac{(d-1)!+1}{d}\) 小 \(1\)，于是有：

\[\begin{cases}p\ 为素数 & \lfloor\frac{(d-1)!+1}{d}-\lfloor\frac{(d-1)!}{d}\rfloor\rfloor=1 \\ p\ 为合数 & \lfloor\frac{(d-1)!+1}{d}-\lfloor\frac{(d-1)!}{d}\rfloor\rfloor=0\end{cases} \]

所以只需统计 \([1,3\times 10^6+7]\) 中的素数即可得出答案。

牛顿迭代

对于在 \([a,b]\) 上连续且单调的函数 \(f(x)\)，牛顿迭代法可用于求解方程 \(f(x)=0\) 的近似解。

初始时先从给定的 \(f(x)\) 和近似解 \(x_0\) 开始，\(x_0\) 可以是随机数。然后我们可以得到 \(f(x_0)\)。

接着，画出与 \(f(x)\) 切于点 \((x_0,f(x_0))\) 的直线 \(l_0\)，将 \(l_0\) 与 \(x\) 轴的交点横坐标记为 \(x_1\)，\(x_1\) 就是更优的近似解。

重复这个迭代过程，可以得到：

\[f'(x_i)=\frac{f(x_i)}{x_i-x_{i+1}} \implies x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)} \]

优点：收敛率是平方级别的，这意味着每次迭代后近似解的精确数位会翻倍。

缺点：不能处理重复的根；解可能在拐点附近发散；解可能在局部极小值或最大值附近振荡；当斜率接近于零时，解可能发散或到达不同的根。

拉格朗日插值法

由 \(n\) 个点可以唯一确定一个多项式 \(y=f(x)\)（不含 \(\log, a^x\)）, 当已知这 \(n\) 个点的坐标要求 \(f(k)\) 有：

\[f(k)=\displaystyle\sum_{i=1}^{n}y_i(\displaystyle\prod_{i\neq j}^{1\leq j\leq n}\frac{k-x_j}{x_i-x_j}) \]

如果已知 \(f(1),f(2),\dots,f(n),f(n+1)\)，要求 \(f(x)\) 有：

\[f(x)=\displaystyle\sum_{i=1}^{n+1}(-1)^{n+1-i}\cdot y_i\cdot\frac{\displaystyle\prod_{j=1}^{n+1}(x-j)}{(i-1)!(n+1-i)!(x-i)} \]

组合计数

• 加法原理（ 分类 ），乘法原理（ 分步 ）。

• 排列：从 \(n\) 个不同元素中取 \(m\) 个排成一列，考虑顺序，产生不同排列的数量为 \(\\ A_n^m\) ( 也可记作 \(P_n^m\) ) \(=\frac{n!}{(n-m)!}=n\times(n-1)\times(n-2)\times\dots\times(n-m+1)\)

• 组合：从 \(n\) 个不同元素中取 \(m\) 个排成一列，不考虑顺序，产生不同组合的数量为 \(\\ \begin{pmatrix}m \\ n\end{pmatrix}=C_n^m=\frac{n!}{m!(n-m)!}=\frac{n\times(n-1)\times\dots\times(n-m+1)}{m\times(m-1)\times\dots\times 2\times 1}\)

  性质：

  1. \(C_n^m=C_n^{n-m}\)
  2. \(C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\)
  3. \(\displaystyle\sum_{i=0}^{n}C_n^i=C_n^0+C_n^1+C_n^2+\dots+C_n^n=2^n\)

• 组合数的应用

1. 有 \(n\) 个完全相同的元素，要求将其分为 \(k\) 组，保证每组至少有一个元素，一共有多少种分法？\(\\\)
   考虑拿 \(k-1\) 块板子插入到 \(n\) 个元素两两形成的 \(n-1\) 个空里面。\(\\\)
   答案为 \(\begin{pmatrix}n-1 \\ k-1\end{pmatrix}\) \(\\\)
   本质是求 \(x_1+x_2+\dots+x_k=n\) 的正整数解的组数。\(\\\)

2. 若问题变换一下，每组允许为空？\(\\\)
   考虑创造条件转化成有限制的问题一，先借 \(k\) 个元素过来，在这 \(n+k\) 个元素形成的 \(n+k-1\) 个空里面插板。\(\\\)
   答案为 \(\begin{pmatrix}n+k-1 \\ k-1\end{pmatrix}=\begin{pmatrix}n+k-1 \\ n\end{pmatrix}\) \(\\\)
   本质是求 \(x_1+x_2+\dots+x_k=n\) 的非负整数解的组数。

3. 再扩展一步，要求对于第 \(i\) 组，至少要分到 \(a_i\) 个元素呢？（ \(\sum a_i\leq n\) ）\(\\\)
   本质是求 \(x_1+x_2+\dots+x_k=n\) 的解的数目。\(\\\)
   类比无限制的情况，我们借 \(\sum a_i\) 个元素过来，保证第 \(i\) 组能至少分到 \(a_i\) 个，也就是令 \(x_i'=x_i-a_i\) 且 \(x_i'\geq 0\) \(\\\)
   得到新方程

   \[(x_1'+a_1)+(x_2'+a_2)+\dots+(x_k'+a_k)=n \]

   转化为

   \[\displaystyle\sum_{i=1}^{k}x_i'=n-\sum a_i \]

   答案为

   \[\begin{pmatrix}n-\sum a_i+k-1\\k-1 \end{pmatrix}=\begin{pmatrix}n-\sum a_i+k-1 \\ n-\sum a_i\end{pmatrix} \]

4. \(1\) ~ \(n\) 这 \(n\) 个自然数选 \(k\) 个，这 \(k\) 个数中两两都不相邻的组合有 \(\begin{pmatrix}n-k+1 \\ k\end{pmatrix}\) 种。

• 二项式定理：

\[(a+b)^n=\displaystyle\sum_{k=0}^{n}C_n^ka^kb^{n-k}\ \ \ \ \ \ \ (ax+by)^n=\displaystyle\sum_{k=0}^{n}C_n^ka^kb^{n-k}x^ky^{n-k} \]

证明可利用数学归纳法，利用 \(\begin{pmatrix}n \\ k\end{pmatrix}+\begin{pmatrix}n \\ k-1\end{pmatrix}=\begin{pmatrix}n+1 \\ k\end{pmatrix}\)

若将二项式定理扩展成多项式的形式，有：

\[(x_1+x_2+\dots+x_t)^n=\displaystyle\sum_{满足\ n_1+n_2+\dots+n_t=n\ 的非负整数解}\begin{pmatrix}n \\ n_1,n_2,\dots,n_t\end{pmatrix}x_1^{n_1}x_2^{n_2}\dots x_t^{n_t} \]

其中 \(\begin{pmatrix}n \\ n_1,n_2,\dots,n_t\end{pmatrix}\) 是多项式系数，满足 \(\displaystyle\sum \begin{pmatrix}n \\ n_1,n_2,\dots,n_t\end{pmatrix}=t^n\)。

• 范德蒙德卷积

\[\displaystyle\sum_{i=0}^{k}\begin{pmatrix}n \\ i\end{pmatrix}\begin{pmatrix}m \\ k-i\end{pmatrix}=\begin{pmatrix}n+m \\ k\end{pmatrix} \]

• \(\text{Lucas}\) 定理：（ \(p\) 是质数，\(1\leq m\leq n\) ）

\[C_n^m\equiv C_{n\ \text{mod}\ p}^{m\ \text{mod}\ p}\times C_{n/p}^{m/p}\ (\text{mod}\ p) \]

• \(\text{Catalan}\) 数列：给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，它们按照某种顺序排成长度为 \(2n\) 的序列，满足任意前缀中 \(0\) 的个数都不少于 \(1\) 的个数的序列的数量为：

\[Cat_n=\frac{C_{2n}^n}{n+1} \]

\(n\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
\(Cat_n\)	\(1\)	\(2\)	\(5\)	\(14\)	\(42\)	\(132\)	\(429\)	\(1430\)	\(4862\)	\(16796\)

以下问题都与 \(\text{Catalan}\) 数有关：

1. \(n\) 个左括号和 \(n\) 个右括号组成的合法括号序列的数量为 \(Cat_n\)
2. \(1,2,\dots,n\) 经过一个栈，形成的合法出栈序列的数量为 \(Cat_n\)
3. \(n\) 个节点构成的不同二叉树的数量为 \(Cat_n\)，\(n\) 个节点的 \(m\) 叉树有 \(\frac{\begin{pmatrix}nm \\ n-1\end{pmatrix}}{n}\)
4. 在平面直角坐标系上，每一步只能向上或向右走，从 \((0,0)\) 走到 \((n,n)\) 并且两个端点外不接触直线 \(y=x\) 的路线数量为 \(2Cat_{n-1}\)
5. 对于一个凸多边形的顶点数为 \(n\)，\(Cat_{n-2}\) 代表所有可能的三角剖分的数量。

• 容斥原理：设 \(S_1,S_2,\dots,S_n\) 为有限集合，\(|S|\) 表示集合 \(S\) 的大小，则：

\[|\displaystyle\bigcup_{i=1}^{n}S_i|=\displaystyle\sum_{i=1}^{n}|S_i|-\displaystyle\sum_{1\leq i<j\leq n}|S_i\bigcap S_j|+\displaystyle\sum_{1\leq i<j<k\leq n}|S_i\bigcap S_j\bigcap S_k|+\dots+(-1)^{n+1}|S_1\bigcap\dots\bigcap S_n| \]

• 第 1 类 \(\mathrm{Stirling}\) 数：\(1\) ~ \(n\) 的排列有 \(m\) 个环：

\[S_1(n,m)=S_1(n-1,m-1)+S_1(n-1,m)\times(n-1) \]

• 第 2 类 \(\mathrm{Stirling}\) 数：\(n\) 个不同的球放入 \(m\) 个相同盒子且盒子非空：

\[S_2(n,m)=S_2(n-1,m-1)+S_2(n-1,m)\times m \]

• 错排数：\(1\) ~ \(n\) 的排列，第 \(i\) 个位置上均不为 \(i\)：

\[D(n)=(n-1)(D(n-1)+D(n-2))=n\times D(n-1)+(-1)^n \]

常用三角函数值

\(\alpha\)	\(\sin\alpha\)	\(\cos\alpha\)	\(\tan\alpha\)	\(\cot\alpha\)
$0\degree $	\(0\)	\(1\)	\(0\)	\(/\)
$15\degree $	\(\frac{\sqrt{6}-\sqrt{2}}{4}\)	\(\frac{\sqrt{6}+\sqrt{2}}{4}\)	\(2-\sqrt{3}\)	\(2+\sqrt{3}\)
$22.5\degree $	\(\frac{\sqrt{2-\sqrt{2}}}{2}\)	\(\frac{\sqrt{2+\sqrt{2}}}{2}\)	\(\sqrt{2}-1\)	\(\sqrt{2}+1\)
$30\degree $	\(\frac{1}{2}\)	\(\frac{\sqrt{3}}{2}\)	\(\frac{\sqrt{3}}{3}\)	\(\sqrt{3}\)
$36.87\degree $	\(\frac{3}{5}\)	\(\frac{4}{5}\)	\(\frac{3}{4}\)	\(\frac{4}{3}\)
$45\degree $	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(1\)	\(1\)
$53.13\degree $	\(\frac{4}{5}\)	\(\frac{3}{5}\)	\(\frac{4}{3}\)	\(\frac{3}{4}\)
$60\degree $	\(\frac{\sqrt{3}}{2}\)	\(\frac{1}{2}\)	\(\sqrt{3}\)	\(\frac{\sqrt{3}}{3}\)
$63.43\degree $	\(\frac{2\sqrt{5}}{5}\)	\(\frac{\sqrt{5}}{5}\)	\(2\)	\(\frac{1}{2}\)
$71.57\degree $	\(\frac{3\sqrt{10}}{10}\)	\(\frac{\sqrt{10}}{10}\)	\(3\)	\(\frac{1}{3}\)
$75\degree $	\(\frac{\sqrt{6}+\sqrt{2}}{4}\)	\(\frac{\sqrt{6}-\sqrt{2}}{4}\)	\(2+\sqrt{3}\)	\(2-\sqrt{3}\)
$75.96\degree $	\(\frac{4\sqrt{17}}{17}\)	\(\frac{\sqrt{17}}{17}\)	\(4\)	\(\frac{1}{4}\)
$90\degree $	\(1\)	\(0\)	\(/\)	\(0\)

• 当 \(\tan x=t\ (x \in \set{x|-\frac{\pi}{2}+2k\pi\leq x\leq\frac{\pi}{2}+2k\pi,k\in\Z})\) 时，\(\sin x=\frac{t\sqrt{t^2+1}}{t^2+1},\cos x=\frac{\sqrt{t^2+1}}{t^2+1}\)

• 当 \(\tan x=t\ (x \in \set{x|\frac{\pi}{2}+2k\pi\leq x\leq\frac{3\pi}{2}+2k\pi,k\in\Z})\) 时，\(\sin x=-\frac{t\sqrt{t^2+1}}{t^2+1},\cos x=-\frac{\sqrt{t^2+1}}{t^2+1}\)

常用数表

\(x\)	\(\ln{x}\)	\(\lg{x}\)	\(\sqrt{x}\)	\(2^x\)	\(3^x\)	\(x^2\)	\(x^3\)	\(x!\)
\(\frac{1}{3}\)	\(-1.0986\)	\(-0.4771\)	\(0.5773\)	\(1.2599\)	\(1.4422\)	\(0.1111\)	\(0.0370\)	\(/\)
\(\frac{1}{2}\)	\(-0.6931\)	\(-0.3010\)	\(0.7071\)	\(1.4142\)	\(1.7321\)	\(0.25\)	\(0.125\)	\(/\)
\(1\)	\(0\)	\(0\)	\(1\)	\(2\)	\(3\)	\(1\)	\(1\)	\(1\)
\(2\)	\(0.6931\)	\(0.3010\)	\(1.4142\)	\(4\)	\(9\)	\(4\)	\(8\)	\(2\)
\(3\)	\(1.0986\)	\(0.4771\)	\(1.7321\)	\(8\)	\(27\)	\(9\)	\(27\)	\(6\)
\(4\)	\(1.3862\)	\(0.6021\)	\(2\)	\(16\)	\(81\)	\(16\)	\(64\)	\(24\)
\(5\)	\(1.6094\)	\(0.6989\)	\(2.2361\)	\(32\)	\(243\)	\(25\)	\(625\)	\(120\)
\(6\)	\(1.7917\)	\(0.7781\)	\(2.4495\)	\(64\)	\(729\)	\(36\)	\(216\)	\(720\)
\(7\)	\(1.9459\)	\(0.8451\)	\(2.6458\)	\(128\)	\(2187\)	\(49\)	\(343\)	\(5040\)
\(8\)	\(2.0794\)	\(0.9031\)	\(2.8284\)	\(256\)	\(6561\)	\(64\)	\(512\)	\(40320\)
\(9\)	\(2.1972\)	\(0.9542\)	\(3\)	\(512\)	\(19683\)	\(81\)	\(729\)	\(362880\)
\(10\)	\(2.3025\)	\(1\)	\(3.1623\)	\(1024\)	\(59049\)	\(100\)	\(1000\)	\(3628800\)

常用常数值

• \(\pi=\arccos(-1)=\sqrt{6\displaystyle\sum^{+\infty}_{i=1}\frac{1}{i^2}}\approx 3.1415926535 \ 8979323846 \ 2643383279 \ 5028841971 \ 6939937510\)

• $e=\displaystyle\lim_{x\to +\infty}(1+\frac{1}{x})^{x=\displaystyle\sum}_{i=0}\frac{1}{i!}\approx 2.7182818284 \ 5904523536 \ 0287471352 \ 6624977572 \ 4709369995 $

• 黄金数 \(\varphi=\frac{\sqrt{5}-1}{2}\approx 0.6180339887 \ 4989484820 \ 4586834365 \ 63811\)

• 真空光速 \(c\approx 299792458 \ \text{m}/\text{s}\)

• 重力加速度 \(g\approx 9.8\ \text{m}/\text{s}^2\) （纬度越高 \(g\) 值越大）

• 阿伏伽德罗常数 \(N_A \approx 6.02214076 \times 10^{23}\text{mol}^{-1}\)

• 引力常量 \(G\approx 6.67\times 10^{-11}\text{m}^3 \text{kg}^{-1} \text{s}^{-2}\)

• 标准状况 STP（\(0\degree \text{C},101.325\text{kPa}\)）下 \(1\text{mol}\) 气体所占的体积约为 \(22.414\text{L}\)

• \(25\degree \text{C},101.325\text{kPa}\)下 \(1\text{mol}\) 气体所占的体积约为 \(24.466\text{L}\)

• 静电力常量 \(k\approx 8.987551\times 10^9 \text{N}\cdot\text{m}^2 \text{/C}^2\)

• 元电荷 \(e=1.60217646283\times 10^{-19}\text{C}\)

• 电子质量 \(m_e=9.11\times 10^{-31}\text{kg}\)

• 电子比荷 \(\frac{e}{m_e}=1.76\times 10^{-11}\text{C / kg}\)

• \(\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots\)

• \(\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots\)

• \(n\log n = \displaystyle\sum_{i=1}^{+\infty}\frac{n}{i}\)

• \(100\) 以内的质数

\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)	\(13\)
\(2\)	\(3\)	\(5\)	\(7\)	\(11\)	\(13\)	\(17\)	\(19\)	\(23\)	\(29\)	\(31\)	\(37\)	\(41\)
\(14\)	\(15\)	\(16\)	\(17\)	\(18\)	\(19\)	\(20\)	\(21\)	\(22\)	\(23\)	\(24\)	\(25\)
\(43\)	\(47\)	\(53\)	\(59\)	\(61\)	\(67\)	\(71\)	\(73\)	\(79\)	\(83\)	\(89\)	\(97\)

精妙的解题方法

常见抽象函数及其模型

• \(f(x\pm y)=f(x)\pm f(y) \implies f(x)=kx\ (k\neq 0)\)

  • \(f(x+y)=f(x)+f(y)\) 证单调性/奇偶性：

    \(\forall x_1,x_2 \in \R,\ x_1<x_2,\ f(x_1)-f(x_2)=f(x_1-x_2+x_2)-f(x_2)=f(x_1-x_2)\)

• \(f(xy)=f(x)+f(y)\ 或 \ f(\frac{x}{y})=f(x)-f(y) \implies f(x)=\log_a x\ (a>0\ 且 \ a\neq 1)\)

  • \(f(xy)=f(x)+f(y)\) 证单调性/奇偶性：

    \(f(1)=f(1)+f(1)=0\ 且\ f(-1)=f(-1)+(1)=0\)

    \(f(1)=f(x)+f(\frac{1}{x})=0\ 且\ f(-1)=f(-x)+f(\frac{1}{x})=0\)

    \(\therefore f(x)=f(-x)\)

• \(f(xy)=f(x)f(y)\ 或 \ f(\frac{x}{y})=\frac{f(x)}{f(y)} \implies f(x)=x^a\)

• \(f(x+y)=f(x)f(y)\ 或 \ f(x-y)=\frac{f(x)}{f(y)} \implies f(x)=a^x\ (a>0\ 且 \ a\neq 1)\)

• \(f(x\pm y)=\frac{f(x)\pm f(y)}{1\mp f(x)f(y)} \implies f(x)=\tan x\ (x\neq k\pi+\frac{\pi}{2},k\in\Z)\)

求值域

• 分离常数 \(\frac{ax+b}{cx+d}=\frac{a}{c}+\frac{ac-bd}{c^2(x+\frac{d}{c})}\)

  例：求 \(f(x)=\frac{x^2-x-1}{x^2+x+1}\) 值域，先求出定义域 \(\R\)。

  \(\frac{x^2-x-1}{x^2+x+1}=1-\frac{2x+2}{x^2+x+1},\text{ }\) 令 \(g(x)=\frac{x^2+x+1}{2x+2}, f(x)=1-\frac{1}{g(x)}\)

  \(g(x)=\frac{x^2+x+1}{2x+2}=\frac{x}{2}+\frac{1}{2x+2}=\frac{x+1}{2}+\frac{1}{2(x+1)}-\frac{1}{2}\)

  对 \(x\) 分类讨论后使用基本不等式。

  \(\begin{cases} x+1\ge 0, x\ge -1, g(x)\geq 2\sqrt{\frac{1}{4}}-\frac{1}{2}=\frac{1}{2} \\ x+1=0, x=-1, g(x) 无意义，f(x)=1 \\ x+1\le 0, x\le -1, g(x)\leq -\frac{3}{2} \end{cases}\)

  综上所述， \(g(x)\in (-\infty,-\frac{3}{2}]\bigcup[\frac{1}{2},\infty)\), \(\frac{1}{g(x)}\in[-\frac{2}{3},0)\bigcup(0,2]\)

  $f(x)\in[-1,\frac{5}{3}], $ 取最值时 \(x=-2 \ \text{or } x=0\)。

• 三角换元（ 形如 \(y=\sqrt{ax+b}+\sqrt{cx-d}\) 求最值 ）

  例：求 \(y=\sqrt{x-4}+\sqrt{18-3x}\) 的值域，先求出定义域 \([4,6]\)。

  令 \(x=4+\sin^2\theta\) 且其中 \(\theta\in[0,\frac{\pi}{2}]\)，除去根号可得值域 \([\sqrt{2},2\sqrt{2}]\)。

• 数形结合（ 将军饮马，圆，斜率... ）

  例 1：求 \(f(x)=\sqrt{(x-1)^2+4}+\sqrt{(x-2)^2+9}\) 最小值？

  转化为求 \((x,0)(1,2)(2,3)\) 之间的距离 答案 \(\sqrt{26}\)。

  例 2：\(f(x)=\frac{\sin x-1}{\sqrt{3-2\cos x-2\sin x}}\ (x\in[0,2\pi])\) 的最小值 ？

  \(\because\ \sin^2x+\cos^2x=1\\\)

  \(\therefore \begin{aligned}f(x)&=\frac{\sin x-1}{\sqrt{\sin^2x-2\sin x+1+\cos^2x-2\cos x+1}}=\frac{\sin x-1}{\sqrt{(\sin x-1)^2+(\cos x-1)^2}}\\&=-\frac{1-\sin x}{\sqrt{(1-\sin x)^2+(1-\cos x)^2}}=-\frac{1}{\sqrt{1+(\frac{1-\cos x}{1-\sin x})^2}}\end{aligned}\)

  当 \(\sin x\neq 1\) 时，令 \(g(x)=(\frac{1-\cos x}{1-\sin x})^2,f(x)=-\frac{1}{\sqrt{1+g(x)}}\)，\(\\\) 显然，\(g(x)\) 的含义是点 \((1,1)\) 与单位圆上的点 \((\sin x,\cos x)\) 的连线的斜率的平方。

  注意到，\(g(x)\geq 0\)，所以 \(f(x)\in [-1,0]\)。

拉格朗日乘数法

偏导数 - 多元函数的导数

当一个函数有多个自变量时，他们共同影响因变量，我们称之为多元函数。比如 \(z=f(x,y)=\sin^2x+\cos^2y\)。

根据导数的定义 \(\displaystyle\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\) 可以类推出偏导数的定义，即

\[\displaystyle\lim_{\Delta x\to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\ \ \ \ \ (1) \\ \displaystyle\lim_{\Delta y\to 0}\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}\ \ \ \ \ (2) \]

其中 \((1)\) 式表示函数 \(z=f(x,y)\) 在点 \((x,y)\) 处对 \(x\) 的偏导数，\((2)\) 式表示函数 \(z=f(x,y)\) 在点 \((x,y)\) 处对 \(y\) 的偏导数。

我们想求 \(f\) 对 \(x\) 的偏导数。如果 \(f\) 是一个一元函数，这个导数可以记作 \(\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}\)。

类似地，当 \(f\) 是多元函数时，这个偏导数就记作 \(\displaystyle\frac{\partial f}{\partial x}\)。

求偏导时，把一个变量当作 \(x\)，其他的变量当作常数，再求导数。

\(\displaystyle E.g.1\ \ \ \ f(x,y)=x+y\ \ \ \ \frac{\partial f}{\partial x}=1+0=1\ \ \ \ \frac{\partial f}{\partial y}=0+1=1\)

\(\displaystyle E.g.2\ \ \ \ f(x,y)=\sin^2x+\cos^2y\ \ \ \ \frac{\partial f}{\partial x}=(\sin^2x)'+0=2\cos x\sin x=\sin 2x\)

拉格朗日乘数法

对于一个函数 \(f(x,y)\) 在附加条件 \(\varphi(x,y)=0\) 下的极值，可以构造三元函数

\[L(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y) \]

求解下面这个方程组，代回原方程就是他的极值点

\[\displaystyle\frac{\partial L}{\partial x}=0 \ \ \ \ \ \ \displaystyle\frac{\partial L}{\partial y}=0 \ \ \ \ \ \ \displaystyle\varphi(x,y)=0 \]

例题 1. 已知 \(x+y=1\)，求 \(x^2+y^2\) 的最值。

常规方法：\(x^2+y^2=x^2+(1-x)^2=2x^2-2x+1\geq\frac{1}{2}\)

拉格朗日乘数法：构造 \(\varphi(x,y)=x+y-1\ \ \ \ \ f(x,y)=x^2+y^2\)

\[L(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)=x^2+y^2+\lambda(x+y) \]

解方程

\[\displaystyle\frac{\partial L}{\partial x}=2x+\lambda=0 \ \ \ \ \ \ \displaystyle\frac{\partial L}{\partial y}=2y+\lambda=0 \ \ \ \ \ \ \displaystyle\varphi(x,y)=x+y-1=0 \]

得到

\[x=\frac{1}{2}\ \ \ \ \ y=\frac{1}{2}\ \ \ \ \ \lambda=-1 \]

最小值即 \(\displaystyle f(\frac{1}{2},\frac{1}{2})=\frac{1}{2}\)。

例题 2. 已知 \(a,b,c\) 均为正实数，\(a^2+b^2+4c^2=1\)，则 \(ab+2ac+3\sqrt{2}bc\) 的最大值为 ？

\[\varphi(a,b,c)=a^2+b^2+4c^2-1\ \ \ \ \ f(a,b,c)=ab+2ac+3\sqrt{2}bc \]

\[L(a,b,c,\lambda)=ab+2ac+3\sqrt{2}bc+\lambda(a^2+b^2+4c^2-1) \]

\[\frac{\partial L}{\partial a}=b+2c+2a\lambda=0 \]

\[\frac{\partial L}{\partial b}=a+3\sqrt{2}c+2b\lambda=0 \]

\[\frac{\partial L}{\partial c}=2a+3\sqrt{2}b+8c\lambda=0 \]

\[\varphi(a,b,c)=a^2+b^2+4c^2-1=0 \]

解得

\[a=\frac{\sqrt{2}}{\sqrt{10}}\ \ \ \ b=\frac{2}{\sqrt{10}}\ \ \ \ c=\frac{1}{\sqrt{10}}\ \ \ \lambda=-\sqrt{2} \]

代回得到

\[f_{\max}=\sqrt{2} \]

练习 1. 将 \(12\) 分为三个正整数 \(x,y,z\) 之和，使得 \(x^3y^2z\) 最大。（ 答案：\(x=6,y=4,z=2\) 时取最大值 \(6912\) ）

练习 2. 已知过定点 \((8,1)\) 的直线 \(l\) 分别交 \(x\) 轴正半轴于点 \(A\)，\(y\) 轴负半轴于点 \(B\)，求 \(|AB|\) 的最小值。

提示：设 \(A(a,0),B(0,b)\) 代入得到 \(\frac{8}{a}+\frac{1}{b}=1,|AB|^2=a^2+b^2\ \ \ \ \ \text{}\) 答案：\(a=10,b=5,|AB|_{\min}=5\sqrt{5}\)

练习 3. 已知 \(x^2+y^2+xy=1\)，求 \(x+y+xy\) 的最小值。

注意此处取等条件并非 \(x=y\)，答案是 \(-\frac{5}{4}\)，取等条件为 \(\begin{cases} x+y=-\frac{1}{2} \\ xy=-\frac{3}{4} \end{cases}\)

泰勒展开在比较大小中的应用

常见的几个式子：

\[e^x\geq 1+x+\frac{x^2}{2}\ \ \ (x\geq 0) \]

\[e^x\leq 1+x+\frac{x^2}{2}\ \ \ (x\leq 0) \]

\[e^x\geq 1+x+\frac{x^2}{2}+\frac{x^3}{6} \]

\[\ln(x+1)\geq x-\frac{x^2}{2}\ \ \ (x\geq 0) \]

\[\sin x\geq x-\frac{x^3}{6}\ \ \ (x\geq 0) \]

\[\sin x\leq x-\frac{x^3}{6}\ \ \ (x\leq 0) \]

\[\cos x\geq 1-\frac{x^2}{2} \]

例题：（ 2022 全国甲卷选择压轴 ）已知 \(\displaystyle a=\frac{31}{32},b=\cos\frac{1}{4},c=4\sin\frac{1}{4}\)，比较 \(a,b,c\) 的大小。

由 \(\cos x\geq 1-\frac{x^2}{2}\) 得 \(b>1-\frac{(\frac{1}{4})^2}{2}=\frac{31}{32}=a\)

由 \(\sin x\geq x-\frac{x^3}{6}\ \ \ (x\geq 0)\) 得 \(c>\frac{95}{96}>a\)

构造函数：取 \(x=\frac{1}{4}\)，则 \(b=\cos x,c=\frac{\sin x}{x}\)，设 \(x=\frac{1}{4}\) 时 \(\cos x<\frac{\sin x}{x}\)，构造 \(f(x)=\sin x-x\cos x\ \ (x>0)\)

\(f'(x)=x\sin x>0\ \ (x\in(0,\frac{1}{4}])\) 故 \(c>b\) 成立，答案为 \(c>b>a\)。

---

• 强制开根号：\(\sqrt{a\pm\sqrt{b}}=\sqrt{\frac{a+\sqrt{a^2-b}}{2}}\pm\sqrt{\frac{a-\sqrt{a^2-b}}{2}}\)。

• 手算根号：首先有一个恒等式

\[\lim_{n\to +\infty}\frac{\sum_{k=0}^{n}\begin{pmatrix}2n\\ 2k\end{pmatrix}x^k([\sqrt{x}])^{2n-2k}}{\sum_{k=0}^{n-1}\begin{pmatrix}2n\\ 2k+1\end{pmatrix}x^k([\sqrt{x}])^{2n-2k-1}}=\sqrt{x} \]

可以变形为

\[\lim_{n\to +\infty}(\sqrt{x}-[\sqrt{x}])^{2n}=0 \]

可以令 \((\sqrt{x}-[\sqrt{x}])^{2n}=\epsilon\)，则 \(\sqrt{x}=\frac{A-\epsilon}{B}\)，\(A,B\) 为二项式展开后有理项正系数和无理项正系数。

注意到 \(\frac{\epsilon}{B}\) 很小，可忽略，因此我们就得到了 \(\sqrt{x}\) 的分数近似。

实际操作：以 \(\sqrt{5}\approx 2.236067977\) 举例，令 \(t=\sqrt{5}-2\)

\(n\)	\(1\)	\(2\)	\(3\)	\(4\)	\(6\)	\(8\)
\(t^n\)	\(-2+\sqrt{5}\)	\(9-4\sqrt{5}\)	\(-38+17\sqrt{5}\)	\(161-72\sqrt{5}\)	\(2889-1292\sqrt{5}\)	\(51841-23184\sqrt{5}\)
	\(\frac{2}{1}=2\)	\(\frac{9}{4}=2.25\)	\(\frac{38}{17}\approx 2.235\)	\(\frac{161}{72}\approx 2.2361\)	\(\frac{2889}{1292}\approx 2.2360681\)	\(\frac{51841}{23184}\approx 2.236067978\)

• 二维空间中欧几里得距离：\(|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)

• 三维空间中欧几里得距离：\(|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\)

• 二维空间中曼哈顿距离：\(|AB|=|x_1-x_2|+|y_1-y_2|\)

• 二维空间中切比雪夫距离：\(d(A,B)=\mathrm{max}(|x_1-x_2|,|y_1-y_2|)\)

• 欧拉公式： \(e^{ix}=\cos x+i\sin x\), 当 \(x=\pi\) 时满足 \(e^{i\pi}+1=0\)

  推导：\(e^{-ix}=\cos (-x)+i\sin (-x)=\cos x - i\sin x\)，两式相加移项得 \(\cos x=\frac{e^{ix}+e^{-ix}}{2}\)

• 二项式定理：\((a+b)^n=\displaystyle\sum_{i=0}^{n}C^{i}_{n}a^{n-i}b^i\)，各二项式系数之和 \(=2^n\)，且奇数项 \(=\) 偶数项。

• \(\text{Fibonacci}\) 通项公式：\(f(x)=\frac{\sqrt{5}}{5}[(\frac{1+\sqrt{5}}{2})^x-(\frac{1-\sqrt{5}}{2})^x]\)

• \(\frac{a}{b}=\frac{c}{d}\implies\) （ 合比定理 ）\(\frac{a+b}{b}=\frac{c+d}{d}\)（ 分比定理 ）\(\frac{a-b}{b}=\frac{c-d}{d}\implies\)（ 合分比定理 ）\(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)

• \(\sin10\degree\sin30\degree\sin50\degree\sin70\degree=\frac{1}{2}\cos20\degree\cos40\degree\cos80\degree=\frac{2\sin20\degree\cos20\degree\cos40\degree\cos80\degree}{4\sin20\degree}=\frac{2\sin40\degree\cos40\degree\cos80\degree}{8\sin20\degree}=\frac{\sin160\degree}{16\sin20\degree}=\frac{1}{16}\)

• 求 \(y=A\sin(\omega x+\varphi)\) 或 \(y=A\cos(\omega x+\varphi)\) 的单调区间：类似 \(\set{x|-\frac{\pi}{2}+2k\pi\leq x\leq\frac{\pi}{2}+2k\pi,k\in\Z}\) 求解可得。

• \(\text{Fibonacci}\) 二平方恒等式：\((a_1^2+a_2^2)(b_1^2+b_2^2)=(a_1b_1-a_2b_2)^2+(a_1b_2+a_2b_1)^2\)，同理还有 \(\text{Euler}\) 四平方恒等式。

• \((ac+bd)^2\leq(a^2+b^2)(c^2+d^2),a,b,c,d\in\R\)

• 已知直线 \(AB,AC\) 的解析式，要求它们的角平分线 \(AT\) 的解析式有：

\[\frac{k_{AT}-k_{AB}}{1+k_{AT}\cdot k_{AB}}=\frac{k_{AC}-k_{AT}}{1+k_{AC}\cdot k_{AT}} \]

化简得：

\[k_{AT}=\frac{k_{AB}\cdot k_{AC}-1\pm \sqrt{k_{AB}^2\cdot k_{AC}^2+k_{AB}^2+k_{AC}^2+1}}{k_{AB}+k_{AC}} \]

• 已知 \(\Delta ABC\) 和点 \(M\) 满足 \(\overrightarrow{MB}+\frac{3}{2}\overrightarrow{MA}+\frac{3}{2}\overrightarrow{MC}=\mathbf{0}\)，\(D\) 为 \(AB\) 中点，则 \(\frac{|\overrightarrow{MD}|}{|\overrightarrow{BM}|}=\ ?\)

  可以将所有点放到一条直线上，让 \(A,C\) 两点重合，得出 \(MB=3MA\)，显然 \(\frac{MD}{BM}=\frac{1}{3}\)。

• 已知 \(\mathbf{a}\neq\mathbf{b},|\mathbf{b}|\neq 0,\forall t\in\R\) 有 \(|\mathbf{a}-t\mathbf{b}|\geq|\mathbf{a}-\mathbf{b}|\) 恒成立

  则 \(\sqrt{(\mathbf{a}-t\mathbf{b})^2}\geq\sqrt{(\mathbf{a}-\mathbf{b})^2}\implies\mathbf{b}^2 t^2-2\mathbf{a}\cdot\mathbf{b}t+2\mathbf{a}\cdot\mathbf{b}-\mathbf{b}^2\geq 0\)

  \(\Delta=4(\mathbf{a}\cdot\mathbf{b})^2-4\mathbf{b}^2(2\mathbf{a}\cdot\mathbf{b}-\mathbf{b}^2)\leq 0\implies\mathbf{b}\cdot(\mathbf{a}-\mathbf{b})=0,\mathbf{b}\perp(\mathbf{a}-\mathbf{b})\)

  也可使用几何法，转化为垂线段最短。

• 如果 \(k,u,v,w>0\) 并且 \(\frac{1}{u^2+k}+\frac{1}{v^2+k}+\frac{1}{w^2+k}=\frac{2}{k}\)，那么

  \[u\sin A+v\sin B+w\sin C\leq \frac{1}{k}\sqrt{(u^2+k)(v^2+k)(w^2+k)} \]

  当且仅当 \(\frac{u^2+k}{u}\sin A=\frac{v^2+k}{v}\sin B=\frac{w^2+k}{w}\sin C\) 或者 \(u\cos A=v\cos B=w\cos C\)

• 小球称重问题

  1. 有 \(N\) 个小球，已知有 \(1\) 个小球比其他小球偏重，使用天平，最少要多少次才能确保找到那个小球 ？（题干改成「偏轻」也可以）
  2. 有 \(N\) 个小球，已知有 \(1\) 个小球和其他小球质量不同，使用天平，最少要多少次才能确保找到那个质量不同的小球（并知道它比其他小球轻还是重）？
  3. 有 \(N\) 个小球，已知有 \(1\) 个小球和其他小球质量不同，使用天平，最少要多少次才能确保找到那个质量不同的小球（无需知道它的轻重）？

  答案分别为 \(\lceil\log_3 N\rceil,\lceil\log_3(2N+3)\rceil,\lceil\log_3(2N+1)\rceil\)

应试要求

• 方程两边同除一个数要写明这个数 \(\neq 0\)，求 \(f(x)\neq 0\) 的解集用 "且" 连接，如求 \(x^2-2x-3\neq 0\) 的解集 \(\implies x\neq 3\) 且 \(x\neq -1\)。

• 保留 \(n\) 位有效数字：从左到右读到第一个不为 \(0\) 的数位后向后继续读 \((n-1)\) 位并四舍五入。

  如对 \(0.0168\) 保留 \(2\) 位有效数字：\(0.017\)

• 集合：考虑空集，条件注意是否有写 “不充分” “不必要” 等字眼

• 不等式：求 \((ax+by)_{min}\) 且已知 \(\frac{n}{x}+\frac{m}{y}=k,x>0,y>0\)，则 \(ax+by=\frac{(ax+by)(\frac{n}{x}+\frac{m}{y})}{k}\)，再用基本不等式化简。

  写明取等条件，例如 \((x=\dots,y=\dots)\)。

• 函数：通过奇偶性求函数解析式需 检验；写出单调区间时用 \(,\) 不用 \(\bigcup\)。

  比如 "\(y=\sin x\) 在第二象限为减函数 " 是错误的，因为第二象限相当于很多个区间取并，即 \((\ \ )\bigcup(\ \ )\bigcup...\bigcup(\ \ )\)，而表示单调性不能用 \(\bigcup\)。

  求出函数表达式需写定义域，并且必须化至最简。

• 二分法精确度：\(f(a)f(b)<0\) 且 \(b-a\le \epsilon\)

• 第 一/二/三/四 象限均不包括 坐标轴。

• 使用 \(A\sin\alpha+B\cos\alpha=\sqrt{A^2+B^2}\sin(\alpha+\arctan{\frac{B}{A}})\) 需写详细过程，不可跳步。

  \(\frac{B}{A}<0\) 时，需检验 \(\varphi\) 位于第二象限还是第四象限。

• 作图题：列表描点，曲线自然，直尺。

• 应用题：求出函数表达式需写定义域，分类讨论取最大值或最小值时需写明 \(\because A>B \ \therefore 选A\)。

  如 \(f(\sqrt{x}+1)=x-2\)，求 \(f(x)=x^2-2x-1\ 且\ x\in [1,+\infty)\)

• 向量：\(|\mathbf{t}|=\sqrt{\mathbf{t}^2}\)；注意向量共线（ 正向 or 反向 ）的情况；回答时写明 大小+方向；几何法不行 \(\to\) 建系；注意与三角函数结合（ 三角换元，出现动点注意坐标用三角函数表示... ）；利用初中技巧（ 倍长中线 ）。

  若已知 \(\mathbf{a}=(1,2)\)，则任意平移 \(\mathbf{a}\) 得到 \(\mathbf{b}\)，因为模长不变，所以 \(\mathbf{b}=(1,2)\)。

• 解三角形：写明 "在...三角形中""由正 / 余弦定理得"；已知 \(\Delta ABC\) 先写 \(A\in(0,\pi)\)，再写 \(A=...\degree\)

  注意：已知 \(\sin x=\sin y\)，则有两种情况：\(x=y\) 或 \(x=\pi -y\)。

• 立体几何：在棱柱（ 包括长方体，正方体等 ）中证明时，只能使用直棱柱的侧棱互相平行且相等这一性质，其余均需证明。

  在空间中，不能用两组对边分别相等证明平行四边形。

• 概率：要写明 \(A,B,\dots\) 是互斥事件 / 对立事件等。枚举时要写明有序 / 无序，有序用 \((A,B)\)，无序用 \(AB\)。记 \(\dots\) 为 \(x_1,x_2\)，则样本点为 \((x_1,x_2)\)。

• 解析几何：讨论斜率存在/不存在，联立之后算 \(\Delta>0\)。

---

暂时写到这里吧，最后更新时间 2024.12.21 17:28。

希望大家都能在 OI / 数学等科目上有所成就 ！