忆点点数论-组合与二项式定理

二项式

二项式定理

\[(a+b)^n = \binom{n}{0}a^0b^n + \binom{n}{1}a^1b^{n-1} + \binom{n}{2} a^2b^{n-2} + \dots + \binom{n}{n-1}a^{n-1}b^1 + \binom{n}{n}a^nb^0 = \sum\limits_{i=0}^n \binom{n}{i}a^ib^{n-i} \]

几何意义：把原式展开，对于 \(a^ib^{n-i}\) 相当于选出 \(i\) 个多项式拿出 \(a\)。

二项式系数的单峰性

我们把 \(\binom{n}{0},\binom{n}{1},\binom{n}{2},\cdots,\binom{n}{n}\) 排成一个序列。那么存在一个 \(t\)，使得 \(1\sim t\) 不降，\(t\sim n\) 不升。

进一步地，若 \(n\) 为奇数，则 \(t=\lceil\dfrac{n}{2} \rceil\)，否则 \(t=\dfrac{n}{2}\) 或 \(\dfrac{n}{2}+1\)。

多项式系数

我们把二项式系数扩展到多项式系数：\(\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}\) 表示把 \(n\) 个物品划分为 \(k\) 个集合，使得第 \(i\) 个集合大小为 \(c_i\) 的方案数。

我们有：

\[\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}=\binom{n}{c_1}\binom{n-c_1}{c_2}\binom{n-c_1-c_2}{c_3}\cdots \binom{n-\sum_{i=1}^{k-1}c_i}{c_k}=\dfrac{n!}{c_1!c_2!c_3!\cdots c_k!} \]

帕斯卡公式

\[\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}=\binom{n-1}{c_1-1 \ c_2\ c_3 \cdots \ c_k}+\binom{n-1}{c_1 \ c_2-1\ c_3 \cdots \ c_k}+\cdots + \binom{n-1}{c_1 \ c_2\ c_3 \cdots \ c_k-1} \]

组合意义：考虑第 \(n\) 个物品被分入了哪一个集合，加法原理即可。

多项式定理

\[(x_1+x_2+\cdots + x_k)^n=\sum_{c_1+c_2+\cdots+c_k=n,c_i\in\mathbb{N}}\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k} x_1^{c_1}x_2^{c_2}\cdots x_k^{c_k} \]

我们把 \((x_1+x_2+\cdots+x_k)^n\) 展开。对于 \(x_1^{c_1}x_2^{c_2}\cdots x_k^{c_k}\) 这一项，会在展开的式子中出现 \(\binom{n}{c_1 \ c_2 \ c_3\ \cdots \ c_k}\) 次。

对展开后的式子合并同类项，最终不同的项会有 \(\binom{n+k-1}{k-1}\) 个（考虑转化为不定方程整数解问题）。

阶乘的素数幂次

设 \(p \in \mathbb{Prime}\)，则有：

\[v_p(n!)=\sum_{i>0} \lfloor\dfrac{n}{p^i} \rfloor \]

其中 \(v_p(x)\) 表示 \(x\) 中可分解出几个 \(p\)。

证明见 P10495 阶乘分解。

我们从另一个角度来计算。用 \(p\) 进制表示 \(n\)，则有 \(n=\sum a_ip^i(0\leq a_i<p)\)。

\[v_p(n!)=\sum_{j\geq1} \lfloor\dfrac{\sum_{i\geq 0}a_ip^i}{p^j}\rfloor = \sum_{i \geq 0}\sum_{j\geq 1} a_i \lfloor p^{i-j}\rfloor =\sum_{i\geq 0}a_i\sum_{j=0}^{i-1}p^{j}=\sum_{i\geq 0}a_i \dfrac{p^i-1}{p-1}=\sum_{i\geq 0} \dfrac{a_ip^i-a_i}{p-1}=\dfrac{n-s_p(n)}{p-1} \]

其中 \(s_p(n)\) 表示 \(n\) 在 \(p\) 进制下各数位的数字之和。

Kummer 定理

\[v_p\left( \binom{n}{m} \right)=v_p\left(\dfrac{n!}{(n-m)!m!}\right)=v_p(n!)-v_p((n-m)!)-v_p(m!)=\dfrac{s_p(m)+s_p(n-m)-s_p(n)}{p-1} \]

假设在 \(p\) 进制下 \(n-m\) 与 \(m\) 相加进了 \(c\) 次位，每进位一次，数位和就会少 \(p-1\)，因此：

\[s_p(n-m)+s_p(m)-c(p-1)=s_p(n) \Rightarrow c=\dfrac{s_p(m)+s_p(n-m)-s_p(n)}{p-1}=v_p\left( \binom{n}{m} \right) \]

于是得到 \(\binom{n}{m}\) 中 \(p\) 的次数，就是 \(n-m\) 与 \(m\) 在 \(p\) 进制下相加进位次数。

同理可得，\(\binom{n}{m}\) 中 \(p\) 的次数就是 \(n\) 与 \(m\) 在 \(p\) 进制下相减的借位次数。

若 \(v_p\left( \binom{n}{m} \right)\not=0\)，那么 \(n,m\) 在 \(p\) 进制下相减时至少产生了一次借位。

换句话说，如果在 \(p\) 进制下存在一位，使得 \(n\) 在这一位的值小于 \(m\) 在这一位的值，那么 \(\binom{n}{m} \bmod p=0\)。

由此可以快速判断 \(\binom{n}{m}\) 的奇偶性：让 \(p\) 为 \(2\)，设 \(n,m\) 在二进制下表示的集合为 \(S_n,S_m\)，
\(\binom{n}{m}\) 为奇数当且仅当 \(S_m \subseteq S_n\)，也就是 \(n \operatorname{and} m = m\)。

组合数

常见计数技巧

捆绑法： 也成整体法，即若要求若干物品相邻，可以将他们视作一个整体来计数。

插空法： 如果要求若干物品两两不相邻，可以先将其他物品放好，然后将这些物品插入空挡当中进行计数。

隔板法： 将不可区分物品分配问题、不定方程整数解问题转化为插板组合问题。

改变计数目标：
如果直接按照题意来计数比较困难，可以尝试通过减法、容斥原理等方法转换成容易求的目标。

改变枚举顺序：
很多时候，计数题要做的基本上是:在某个范围内枚举元素，计算它们的和。直接按照题意来做显然只能拿到暴力分, 我们往往需要安排一个合适的顺序来计算。

等价替代（映射）：
构造一个映射，将每一种原问题的方案映射为新问题的一种方案，并使答案更容易计算。例如捆绑法，插空法，隔板法等。

1. 帕斯卡公式（杨辉三角）

\[\dbinom{n}{m}=\dbinom{n-1}{m-1}+\dbinom{n-1}{m} \]

意义：从 \(n\) 个中选出 \(m\) 个元素，若第 \(n\) 元素选，则前面的选择方案为 \(\binom{n-1}{m-1}\) ，若不选，则前面的选择方案为 \(\binom{n-1}{m}\)。

2.组合数求法

· 使用帕斯卡定理可 \(O(N^2)\) 的时间内预处理组合数。

· 当模数较小时，可用卢卡斯定理在 \(O(log_{mod}{N})\) 的时间复杂度内求出组合数。

· 若模数为质数，可求 \((n-m)!m!\) 的逆元来求解。

· 若是高精，考虑将三个阶乘 \(O(N)\) 分解质因数，随后合并，然后乘出来。

3.组合恒等式

吸收恒等式

\[\dbinom{n}{m}=\frac{n}{m}\dbinom{n-1}{m-1} \]

证明：

\[\begin{aligned} \dbinom{n}{m}&=\frac{n!}{(n-m)!m!}\\ &=\frac{n}{m}\frac{(n-1)!}{[(n-1)-(m-1)](m-1)!}\\ &=\frac{n}{m}\dbinom{n-1}{m-1} \end{aligned} \]

同理可得：

\[\binom{n}{m}=\dfrac{n}{n-m} \times \binom{n-1}{m} \]

\[\binom{n}{m}=\dfrac{n-m+1}{m} \times \binom{n}{m-1} \]

对称恒等式

\[\binom{n}{m}=\binom{n}{n-m} \]

上指标求和

1.

\[\sum_{i=0}^n \binom{m+i}{m}=\binom{n+m+1}{m+1} \]

证明：

\[\begin{aligned}\sum_{i=0}^n \binom{m+i}{m} &= \binom{m}{m} +\binom{m+1}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+1}{m+1} + \binom{m+1}{m} + \binom{m+2}{m} + \dots + \binom{m+n}{m}\\ &= \binom{m+2}{m+1} + \binom{m+2}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+3}{m+1} + \binom{m+3}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+n+1}{m+1}\end{aligned} \]

2.

\[\sum_{i=k}^{n} \binom{i}{k}=\binom{n+1}{k+1} \]

证明：

\[\begin{aligned} \sum_{i=k}^{n} \dbinom{i}{k} &= \sum_{i=0}^{n-k} \dbinom{k+i}{k}\\ &=\dbinom{(n-k)+k+1}{k+1}\\ &=\dbinom{n+1}{k+1} \end{aligned} \]

组合意义：考虑 \(k+1\) 个物品放到 \(n+1\) 个位置中，若最后一个物品在第 \(i\) 个位置，则此时方案数为 \(\binom{i-1}{k}\)。

对角线求和

\[\sum_{i=0}^{m}\binom{n+i}{i} =\sum_{i=0}^{m}\binom{n+i}{n}=\binom{n+m+1}{n+1} \]

易证。

下指标求和

1.

\[\sum_{i=0}^n\binom{n}{i}=2^n \]

代数意义：\((1+1)^n\)。

证明显然。

2.

\[\sum_{i=1}^n \binom{n}{i}i=n \times 2^{n-1} \]

证明：

\[\begin{aligned} \sum_{i=1}^n \binom{n}{i}i &= \sum_{i=1}^n \binom{n-1}{i-1}\dfrac{n}{i} \times i \\ &=n\sum_{i=1}^n \binom{n-1}{i-1} \\ &= n \sum_{i=0}^{n-1} \binom{n-1}{i}\\ &= n \times 2^{n-1} \end{aligned} \]

下指标交错和

\[\sum_{i=0}^n(-1)^i\binom{n}{i}=0 \]

代数意义：\((1-1)^n\)

组合意义：在 \(n\) 个物品中选奇数个物品和选偶数个物品的方案数相同。以选偶数个物品为例，最后一个若选，则要从前面 \(n-1\) 个物品中选出奇数个。最后一个若不选，则要在前面 \(n-1\) 个里选偶数个。合起来方案数为 \(2^{n-1}\) 。奇数个同理，因此方案数相同。

组合数前缀和

设 \(S_{n,m}=\sum_{i=0}^{m} \binom{n}{i}\)。则有

\[S_{n,m}=S_{n-1,m}+S_{n-1,m-1} \]

\[S_{n,m}=S_{n,m-1}+\binom{n}{m}=S_{n,m+1}-\binom{n}{m+1} \]

证明：

\[\begin{aligned} S_{n,m}&=\sum_{i=0}^m\binom{n}{i}\\ &=\sum_{i=1}^m\left[\binom{n-1}{i}+\binom{n-1}{i-1} \right]+\binom{n}{0}\\ &=\sum_{i=0}^m\binom{n-1}{i}+\sum_{i=1}^m\binom{n-1}{i-1}\\ &=\sum_{i=0}^m\binom{n-1}{i}+\sum_{i=0}^{m-1}\binom{n-1}{i}\\ &=S_{n-1,m}+S_{n-1,m-1} \end{aligned} \]

第二个显然。

范德蒙德卷积

\[\sum_i \binom{n}{i}\binom{m}{k-i}=\binom{n+m}{k} \]

从集合 \(A\) 中选 \(x\) 个，集合 \(B\) 中选 \(y\) 个，当 \(x+y\) 为定值直接用。

若 \(x-y\) 为定值，转化成在 \(B\) 集合中不选 \(m-y\) 个，则从 \(n+m\) 个中选出 \(m+x-y\) 个，可直接使用。

搭路计数

从 \((0,0)\) 只向下或向右走到 \((n,m)\) 的方案数为 \(\binom{n+m}{n}\)。

从 \(n+m\) 次操作中选出 \(n\) 次向下操作。

不定方程整数解个数

Problem A.

现有 \(k\) 个未知数 \(x_1,x_2,x_3,...x_k\)，求不定方程 正整数解 的个数：\(\sum x_i=n\)。

隔板法可得方案 \(\binom{n-1}{k-1}\)。

Problem B.

现有 \(k\) 个未知数 \(x_1,x_2,x_3,...x_k\)，求不定方程 非负整数 解 的个数：\(\sum x_i=n\)。

变成了可以为空的隔板法，方案个数为 \(\binom{n+k-1}{k-1}\)。

多重集概念

概念：确定的、无序的、可重的集合。

Problem A.

现有一个多重集合 \(S=\{c_1\cdot x_1,c_2\cdot x_2,...c_k\cdot x_k\}\)，\(\sum c_i=n\)。

\(S\) 的排列数为：

\[\frac{n!}{c_1!c_2!\cdots c_k!} \]

Problem B.

现有一个多重集合 \(S=\{\infty\cdot x_1,\infty\cdot x_2,...\infty\cdot x_k\}\)
。

我们任意地取出 \(S\) 的 \(m\) 个元素生成一个集合，问会形成多少种不同的集合？

问题转化为不定方程非负整数解问题：\(\sum x_i=m\) 的解个数。

答案就是 \(\binom{k+m-1}{k-1}\)。

卢卡斯定理（Lucas）

\[\binom{n}{m} \equiv \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} \times \binom{n \bmod p}{m \bmod p} \pmod{p} \]

\(p \in \mathbb{Prime}\)

就是把 \(n,m\) 表示为 \(p\) 进制数，对每一位分别求解再相乘。

证明：

引理：\((1+x)^p\equiv 1+x^p \pmod{p}\)

\[\begin{aligned} (1+x)^p&\equiv\sum_{i=0}^{p}\dbinom{p}{i}x^i \pmod{p}\\ &\equiv \sum_{i=1}^{p-1}\frac{p}{i}\dbinom{p-1}{i-1}x^i+\dbinom{p}{0}x^0+\dbinom{p}{p}x^p \pmod{p}\\ \end{aligned} \]

因 \(\frac{p}{i}\binom{p-1}{i-1}x^i\) 定为整数，且因 \(p\) 为质数，\(i\!\not|p\)，所以 \(\frac{p}{i}\binom{p-1}{i-1}x^i\equiv 0\pmod{p}\)。

原式便与 \(1+x^p\) 同余。

设 \(n\) 为 \(sp+q\)，\(m\) 为 \(tp+r\)。问题变为证明 $\binom{n}{m}\equiv \binom{s}{t}\times\binom{q}{r} $。

\[\begin{aligned} (1+x)^p&\equiv (1+x)^{sp+q} \pmod{p}\\ &\equiv (1+x)^{sp}\times (1+x)^{q} \pmod{p}\\ &\equiv [(1+x)^p]^s\times (1+x)^q \pmod{p}\\ &\equiv (1+x^p)^s\times (1+x)^q \pmod{p}\\ &\equiv (\sum_{i=0}^{s}\binom{s}{i}x^{ip})(\sum_{i=0}^{q}\binom{q}{i}x^{i}) \pmod{p}\\ \end{aligned} \]

$\binom{n}{m} $ 即为 \(x^m\) 的系数。而 $x^m=x=x^{tp}\times x^r \(，\)x^m$ 的系数也可表示为 \(\binom{s}{t} \times \binom{q}{r}\) 且对于任意 \(x\) 都满足。
所以 \(\binom{n}{m} \equiv \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} \times \binom{n \bmod p}{m \bmod p} \pmod{p}\)。

证毕。

卡特兰数

对于一个长度为 \(2n\) 的 01 序列 \(A\)，含有 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，满足对于任意的 \(i \in [1,2n]\)，\(A[1\sim i]\) 中 \(1\) 的个数不超过 \(0\) 的个数。

这样的 \(A\) 的个数，我们记为 \(Cat_n\)，也就是卡特兰数的第 \(n\) 项。

\(Cat_n\) 式子：

\[Cat_i=\binom{2n}{n}-\binom{2n}{n+1}=\dfrac{\binom{2n}{n}}{n+1} \]

\[Cat_n=\frac{Cat_{n-1}\ \times(4n-2)}{n+1} \]

\[Cat_i=\sum_{j=1}^i (Cat_{i-1}\times Cat_{i-j}) \]

求法：

考虑容斥。

总的方案数为 \(\binom{2n}{n}\) 个。

对于不合法的序列集合 \(B\) 中的每个元素 \(x\)，\(x\) 序列中存在一个位置 \(2p+1\)，前面有 \(p\) 个 \(0\)，\(p+1\) 个 \(1\)。将后面的 \(0\) 和 \(1\) 翻转，便得到一个有 \(n+1\) 个 \(1\)，\(n-1\) 个 \(0\) 的序列。将此种序列组成的集合称为 \(C\)，则 \(B \subseteq C\)。

对 \(C\) 集合中的每个元素也可做同样转换对应到 \(B\) 的一个元素，则又有 \(C \subseteq B\)，即 \(C=B\)，构成双射。

则不合法的方案数也是 \(C\) 集合的元素个数，即 \(\binom{2n}{n+1}\)，合法方案数便为 $\binom{2n}{n}-\binom{2n}{n+1} $。

证毕。

第二种求法：

\(Cat_n\) 也可以表述为：在平面直角坐标系中，每次允许向 \(x\) 或 \(y\) 的正方向移动一格，从 \((0,0)\) 不超过 \(y=x\) 这条直线走到 \((n,n)\) 的方案数。

那么如果我们移动过程中触碰到了 \(y=x+1\) 这条直线，必定不合法。

考虑将所有碰到 \(y=x+1\) 这条直线的路径方案在碰到直线后的路径进行翻转，便会得到一条从 \((0,0)\) 走到 \((n-1,n+1)\) 的路径，如图：

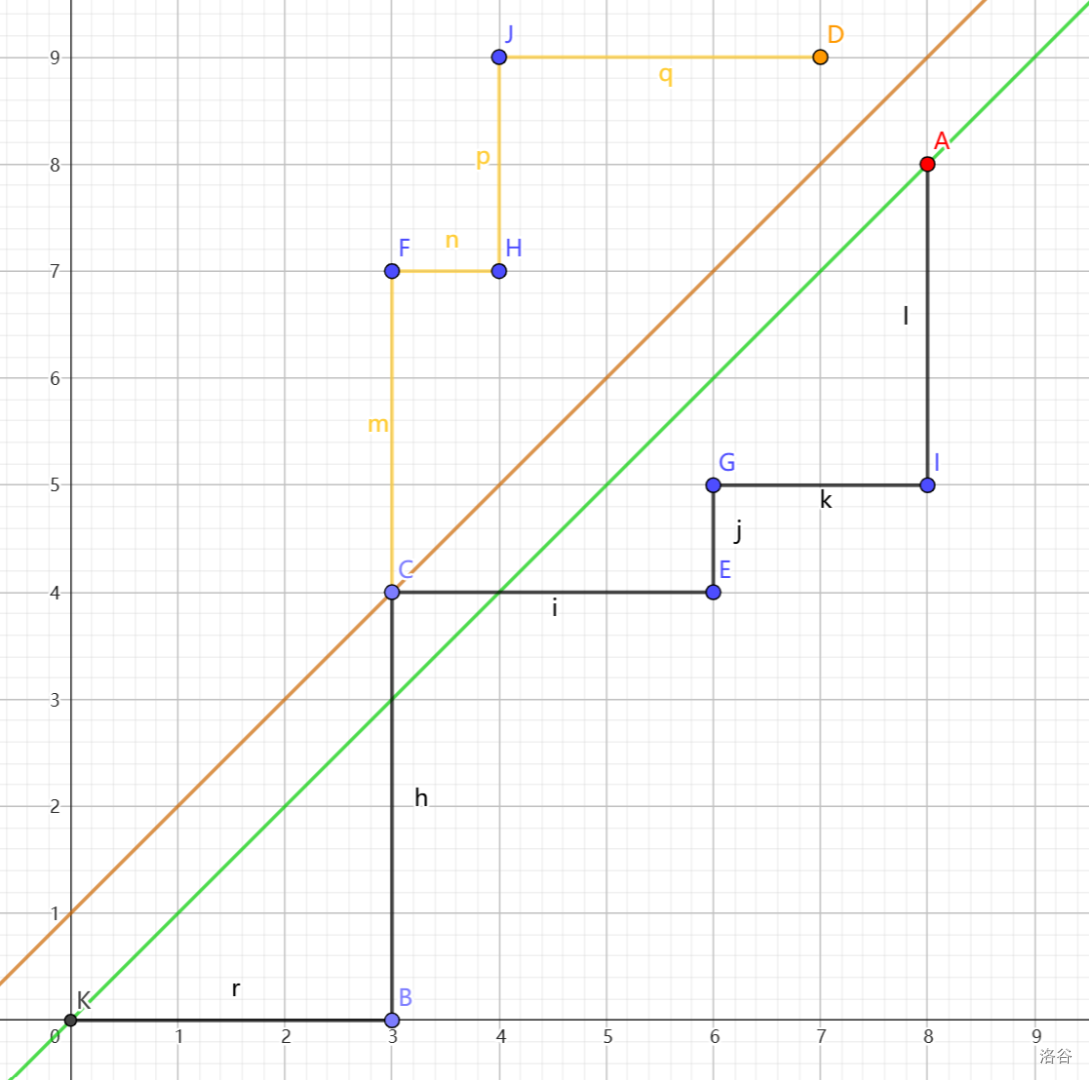
图中黑色折线为原路径，黄色折线为 “反射” 得到的直线。

那么不合法的走法有 \(\binom{2n}{n+1}\) 种，也可以得到与求法 1 相同的表达式。

卡特兰数的应用

长度为 \(2n\) 的括号序列个数为 \(Cat_n\)；

\(n\) 个元素按顺序进栈，出栈序列的个数为 \(Cat_n\)；

\(n\) 个节点能够构造出 \(Cat_n\) 种不同的二叉树。

设 \(f(n)\) 为 \(n\) 个节点构成的不同二叉树的数量。该问题答案为 不同情况下左子树的方案数 \(\times\) 对应右子树的方案数 的和。即 \(f(n)=f(0)\times f(n-1)+f(1)\times f(n-2)+\cdots+f(n-1)\times f(0)=\sum_{i=1}^nf(i-1)\times f(n-i)\)，发现与卡特兰数的递推式相同，故答案为 \(Cat_n\)。

卡特兰数的前十项（从 \(0\) 开始）：

\[1,1,2,5,14,42,132,429,1430,4862,... \]

第二类斯特林数（简称 \(S2\) ）

定义：为将n个物体划分成k个非空的没有区别的集合的方法数，大致就是把 n 个不同的小球放入m个相同的盒子中（且盒子不能为空）的方案数。设 $s[i][j] $ 表示前 \(i\) 个小球放入前 \(j\) 个盒子里的方案数，则递推公式为：

\[s[i][j]=s[i-1][j]*j+s[i-1][j-1] \]

可以看成把第 \(i\) 个球放到前 \(j-1\) 个盒子中和放入第 \(j\) 个盒子中的方案和。

通式：

\[S2(n,m)=\sum_{i=0}^{m}{(-1)^{m-i}\cdot \dbinom{m}{i}\cdot i^n} \]

end。。。