Control of Mobile Robots 学习笔记(二、三)Mobile robot, Linear system
《Control of mobile robot》是Gatech的Dr. Magnus Egerstedt在Coursera上发布的一个公开课(现在好像没在Coursera了,这位老师也不在Gatech了)。之前没有自主移动机器人方面的基础,学习的同时记录一下。
课件是从github上下载的。
Module 2 (Mobile robot) 介绍了移动机器人的基础知识,Module 3 (Linear system) 介绍了线性系统;
Module 2 (Mobile robot)
- Differential drive robot kinematic model (略)
- Unicycle model
Module 3 (Linear system)
- What is linear system ?
- Car model, pendulum, unicycle model are linear system ?
- Linearization
- How Linear system behave ?
- Stability
- Rendezvous problem
Unicycle model
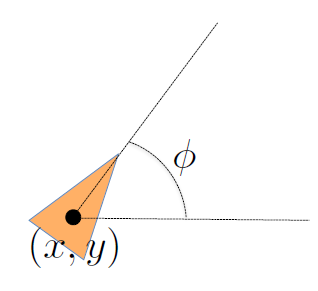
如图所示为unicycle model。
- 控制量u: v, w (赋给机器人的线速度和角速度)
- 状态x: x,y,theta (or phai in figure),(状态是全局坐标系下机器人的坐标)
Unicycle model的动力学描述,给机器人的线速度和角速度控制命令与机器人在全局坐标系中的位姿变化关系。具体关系如下:
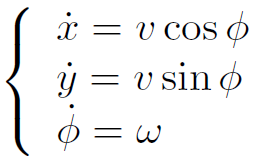
x 与线速度和转向角有关
y 也与线速度和转向角有关
phai 与角速度有关(转向角的变化率就是角速度)
What is linear system ?
我们需要一个更一般的模型去描述现实中的系统。线性系统(linear model)是一种可以描述一部分系统的模型。
设想一个系统,它是一维运动的质点,且加速度直接被控制,也就是加速度a = u。
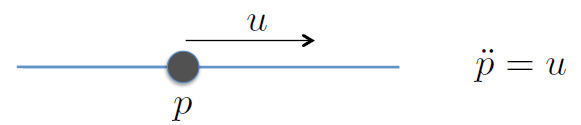
状态是二维状态(位置,速度)。 用预测模型描述动力学的话如图所示:
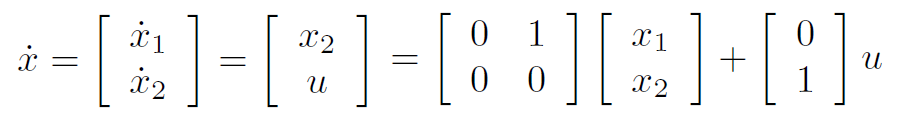
系统的输出 y = (1 0) x
可以把它总结为如图所示的通用形式:
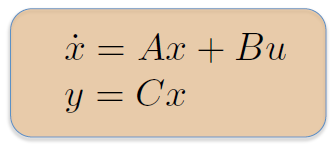
把可以用这种形式表述的系统称为线性时不变系统(Linear Time-Invarient system, LTI)。
Car model, pendulum, unicycle model are linear system ?
从Car model的动力学得知,
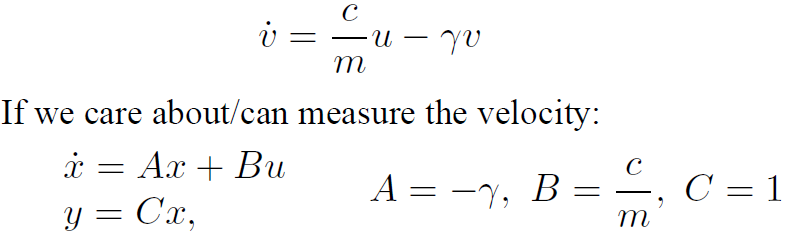
可以确定A,B,C三个矩阵(标量也是1x1的矩阵),因此,Car model是线性时不变系统。
Pendulum的物理学原理得知:
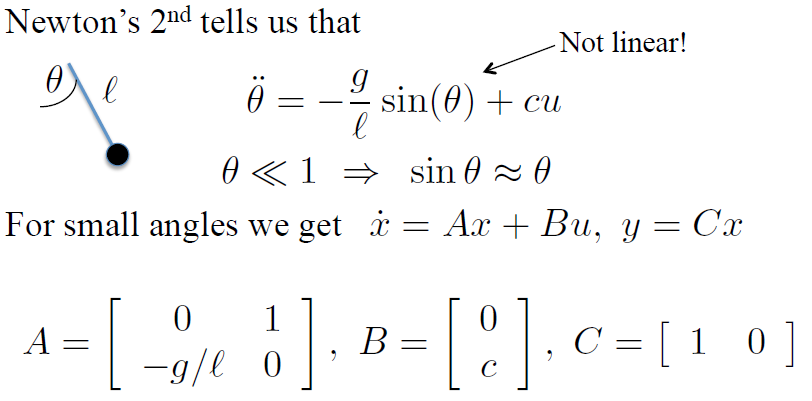
状态theta是在sin里面,不是线性的。但是theta很小的时候,sin(theta) 约等于 theta,这时是LTI。
Unicycle model的动力学在上面分析过,状态phai在sin或者cos里面,同样不是LTI。即使是phai很小改变公式到如图所示,也同样不是LTI

控制量v和phai相乘在一起了,依旧不是LTI。
结论:
- Car model √, 是LTI
- Pendulum ×,theta很小的时候是LTI
- unicycle model ×
Linearization
现实世界中几乎很少的系统是LTI,大部分是非线性系统。但是我们把一个非线性系统在它一个操作点线性化,即在它的操作点附近近似线性系统。
(推导过程忽略,直接放结果)
假设通用非线性系统为: x = f(x, u), y = h(x); x, u, y, f, h 都可以是矩阵。
那么A,B,C是 f关于x,f关于u,h关于x的Jaccobian matrix (雅克比矩阵)。
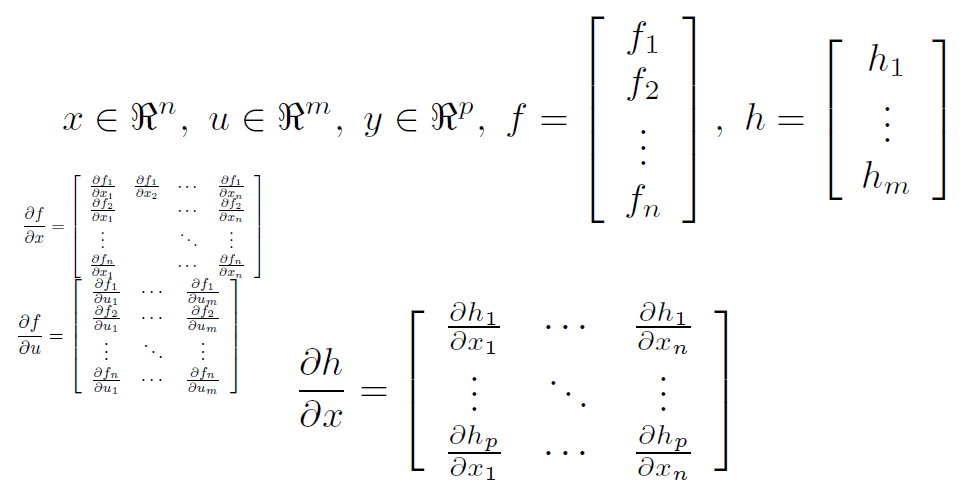
根据这个,可以求出一些(不全是)非线性系统在某一点的系统特性。
- Pendulum √, 在(0,0)点处的系统特性可以通过线性化得到
- Unicycle ×,非线性化之后x2 dot =0, 即关于y方向的变化为0。不符合事实。所以unicycle model不能线性化
How Linear system behave ?
phai(t,t0) is state transmission matrix (状态转移矩阵), is a exponential matrix.

系统的状态和初始状态,状态转移矩阵,控制量的累积有关。
Stability
线性系统的状态是标量的时候,系统稳定的条件是:

换到向量的时候,一个系统稳定的条件如下:
渐进稳定 当且仅当 状态转移矩阵的所有特征值的实部<0;
严格稳定 仅当 状态转移矩阵的所有特征值的实部<=0; (这里包括:一个特征值为0,其余的特征值实部小于0; 或者一部分特征值是仅有虚部的,其余特征值的实部都<0)
Rendezvous problem
对于swarm robotics (群体机器人)的Rendezvous(聚集)问题中,系统是否稳定的判断:
判断依据是状态转换矩阵的特征值是否满足稳定(渐进稳定或者严格稳定)的条件。
对于多机器人来说,状态转换矩阵是根据图论得知,是图的laplacian matrix: L, 它的特点是一个特征值是0,其余的都是大于零。
因此,对于系统 xdot = -Lx
来说是严格稳定的;

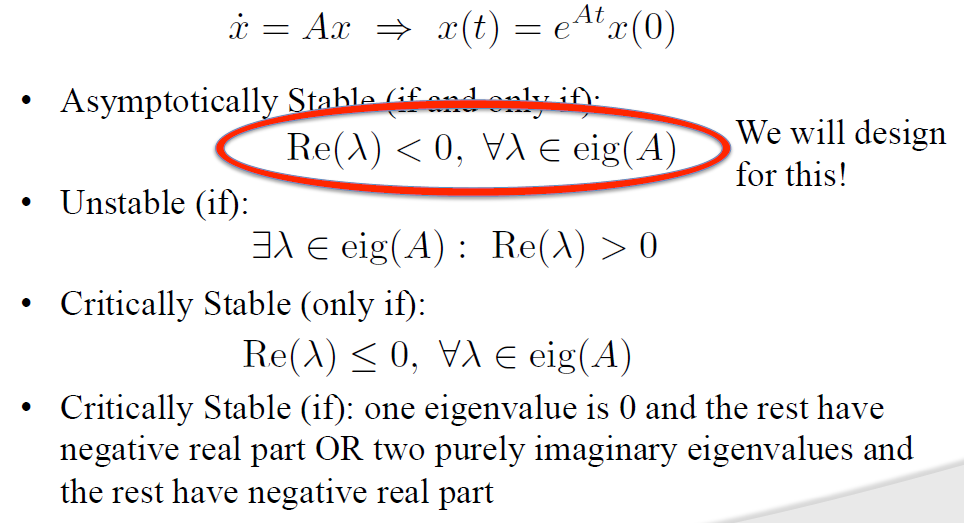

 浙公网安备 33010602011771号
浙公网安备 33010602011771号