树状数组
树状数组(至少在我眼里)是一种简洁而优雅的数据结构。
它可以以 O ( log n ) 的速度实现单点修改和区间查询。(当然也可以在修改后实现区间修改和单点查询、区间修改和区间查询等操作)
树状数组能解决的问题都能被线段树解决,但树状数组常数更优,代码更简洁。
一、树状数组的概念和lowbit
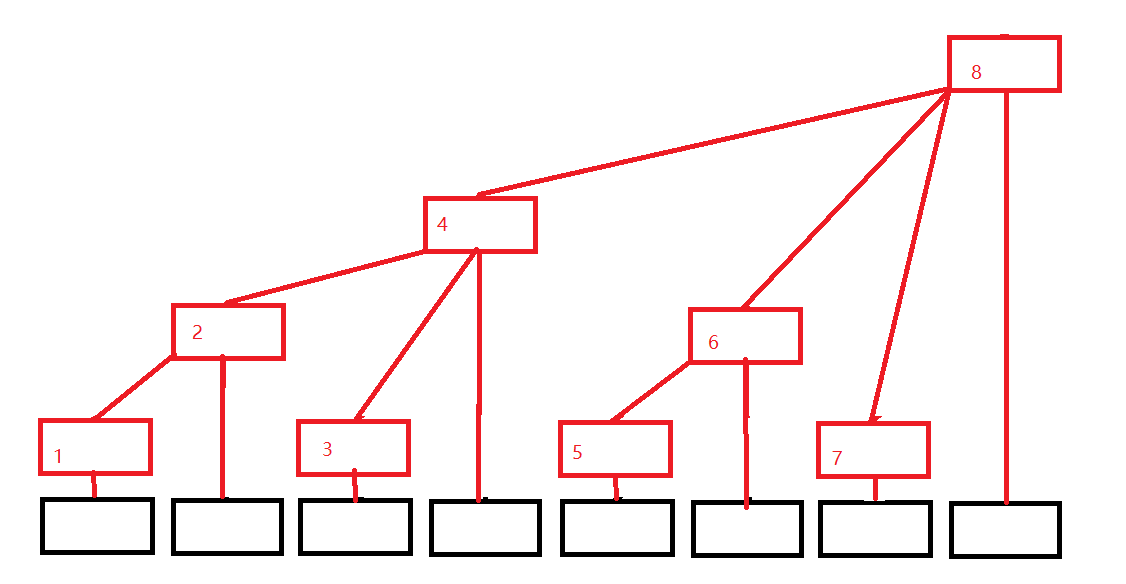
如图,设树状数组为 c [ ] ,则
c [ i ] = c [ i ] + c [ i - 1 ] + ... + c [ i - 2k + 1 ]
根据网上的说法,k 为 i 的二进制位中最低位开始连续 0 的长度。
我把 k 理解为 i 的最大 2 整数次幂因子(反正结果一样,能理解就行吧)
那如何求得 2k 呢?
lowbit
令 lowbit ( i ) = 2k ,则 lowbit ( i ) = i & ( - i ) 。
负数的存储方式是,将负数绝对值二进制取反然后加一(这种存储方式使正负数能直接运算(溢出))。
(证明懒得写了)
二、单点修改&区间求值:更新与查询操作
1.树状数组的更新
在更新 c [ i ] 时,我们需要更新 c [ i ] 的所有父节点。而 f ( c [ i ] ) = c [ i + lowbit ( i ) ]
不写证明了,我的理解是,树状数组的每个部分都可以看作 1 ... 2n 部分树的平移。
void add(int i,int k){ while(i<=n) c[i]+=k,i+=lowbit(i); return; }
2.区间查询
sum [ l,r ] = sum [ 1,r ] - sum [ 1,l - 1 ]
关于 sum [ 1,i ],c [ i ] 包含的最后一个点是 a [ i - lowbit ( i ) + 1 ] (原数组)。
则 sum [ 1,i ] = c [ i ] + sum [ 1,i - lowbit ( i ) ] 。
inline int sumup(int x){ int res=0; while(x>0) res+=c[x],x-=lowbit(x); return res; }
求值时
int l=read(),r=read(); printf("%d\n",sumup(r)-sumup(l-1));
3.线性初始化
在建立树状数组时,自然可以对每个 a [ i ] 进行一次更新操作,时间复杂度为 O ( n log n ) 。
不过在运用前缀和的情况下,可以实现线性复杂度的树状数组初始化。
for(int i=1;i<=n;i++) pre[i]=pre[i-1]+read(),c[i]=pre[i]-pre[i-lowbit(i)];
因为不需要存储 a [ i ] ,空间复杂度不变。
4.模板
洛谷P3374:
#include<bits/stdc++.h> #define N 500001 using namespace std; int n,m,c[N],pre[N]={0}; inline int lowbit(int x){ return x&(-x); } void add(int i,int k){ while(i<=n) c[i]+=k,i+=lowbit(i); return; } inline int sumup(int x){ int res=0; while(x>0) res+=c[x],x-=lowbit(x); return res; } inline int read(){ int res=0; bool t=true; char ch=getchar(); while(ch<'0'||ch>'9'){ if(ch=='-') t=false; //警钟长鸣,快读记得写负数 ch=getchar(); } while(ch>='0'&&ch<='9') res=(res<<1)+(res<<3)+ch-48,ch=getchar(); if(!t) return(0-res); return res; } int main(){ n=read(),m=read(); for(int i=1;i<=n;i++) pre[i]=pre[i-1]+read(),c[i]=pre[i]-pre[i-lowbit(i)]; for(int i=1;i<=m;i++){ int num=read(); if(num==1){ int x=read(),k=read(); add(x,k); } else{ int l=read(),r=read(); printf("%d\n",sumup(r)-sumup(l-1)); } } }
三、区间更新&单点查询
引入差分数组 d [ i ] = a [ i ] - a [ i -1 ]。
若更新区间 [ l,r ] ,则只需要更新 d [ l ] 和 d [ r + 1 ] 。
#include<bits/stdc++.h> #define N 500001 using namespace std; int n,m,d[N],a[N]; inline int lowbit(int x){ return x&(-x); } void add(int x,int k){ while(x<=n) d[x]+=k,x+=lowbit(x); return; } inline int sumup(int x){ int res=0; while(x>0) res+=d[x],x-=lowbit(x); return res; } inline int read(){ int res=0,flag=1; char ch=getchar(); while((ch<'0'||ch>'9')&&ch!='-') ch=getchar(); if(ch=='-') flag=-1,ch=getchar(); while(ch>='0'&&ch<='9') res=(res<<1)+(res<<3)+ch-48,ch=getchar(); return flag*res; } int main(){ n=read(),m=read(); for(int i=1;i<=n;i++) a[i]=read(),d[i]=a[i]-a[i-lowbit(i)]; for(int i=1;i<=m;i++){ int t=read(); if(t==1){ int x=read(),y=read(),k=read(); add(x,k); add(y+1,-k); } else{ int x=read(); printf("%d\n",sumup(x)); } } }
四、区间更新&区间查询
sum [ i ] = a [ 1 ] + a [ 2 ] + ... + a [ i ]
= ( d [ 1 ] ) + ( d [ 1 ] + d [ 2 ] ) + ... + ( d [ 1 ] + d [ 2 ] + ... + d [ i ] )
= n d [ 1 ] + ( n - 1 ) d [ 2 ] + ... + d [ i ]
= n a [ i ] - d [ 2 ] - 2 d [ 3 ] - ( i - 1 ) d [ i - 1 ]
= n ( d [ 1 ] + d [ 2 ] + ... d [ i ] ) - ( 1 * d [ 2 ] + 2 * d [ 3 ] + ( i - 1 ) * d [ i ] )
令 d1 = d,需要维护两个树状数组,d2 [ i ] = d1 [ i ] * ( i - 1 ) 。
未测试模板:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号