求二叉树中节点间的宽度

标题：求二叉树中节点间的宽度

题目链接：https://www.luogu.com.cn/problem/T236448?contestId=67903

题目描述

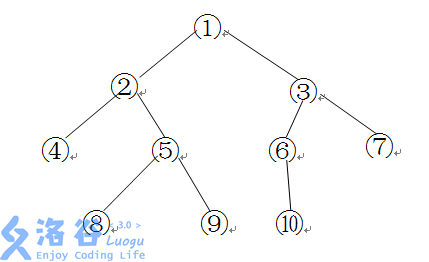
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：4 宽度：4（同一层最多结点个数）

结点间距离： ⑧→⑥为8 (3×2+2=8)

⑥→⑦为3 （1×2+1=3）

注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，

与由根向叶结点方向（下行方向）时的边数之和。

输入格式

输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。

输出格式

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。

输入输出样例

输入 #1复制

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

输出 #1复制

4
4
8

解题思路：
1.首先，要明确这道题要求的是三个问题：深度，宽度，两结点距离
2.深度比较好理解，因为题目的输入格式已经把各个结点的根结点和父亲结点告诉了我们，因此只需要用数组记录一下根结点和子结点，子结点的深度是根结点加一，最后找最大的输出就好了。
3.宽度是在深度的基础上，每当有深度相同的结点，都把宽度加一，最后一样的方法找最大。
4.两结点间的距离需要用到lca，这是一个专门用于二叉树的dfs，要点是把两结点递归到同一深度之后，比较它们的根节点是否相同，相同则返回上一级。

参考代码：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int fa[101],root[101],son[101];
int depth[101],width[101];
int dfs(int n,int m){
if(n==m){
return n;//父亲结点相同时，结束递归
}
else if(depth[n] == depth[m]){
return dfs(fa[n],fa[m]);//深度相同，返回上一级
}
else if(depth[n] < depth[m]){
return dfs(n,fa[m]);//深度不同，只有一边递归
}
else{
return dfs(fa[n],m);//同上
}
}
int main(){
cin >> n;
depth[1] = 1;
for(int i = 1;i < n;i++){
cin >> root[i] >> son[i];//记录根节点和子结点
depth[son[i]] = depth[root[i]] + 1;//子结点的深度是根节点加一
fa[son[i]] = root[i];//记录父亲结点，为lca做准备
}
int a,b;
cin >> a >> b;
int max_depth = 1;
for(int i = 1;i <= n;i++){
max_depth = max(max_depth,depth[i]);//找出最大的深度
width[depth[i]]++;//一旦有深度相同的结点，宽度加一
}
cout << max_depth << endl;
int max_width = 1;
for(int i = 1;i <= n;i++){
max_width = max(max_width,width[i]);//找出最大宽度
}
cout << max_width << endl;
int k = dfs(a,b);
cout << (depth[a] - depth[k]) * 2 + depth[b] - depth[k];
return 0;
}