大津法实现图像二值化

算法步骤

 

　　1、生成灰度直方图，并进行归一化，得到比例直方图。

　　2、根据比例直方图计算整幅图像的平均灰度$\mu_0$。

　　3、从灰度0迭代到灰度255，每次迭代计算背景（这里将小于当前迭代灰度的部分视为背景）占整幅图像的比例$\omega_1$；计算背景的平均灰度$\mu_1$；计算前景和背景的类间方差$\sigma^2 = \frac{\omega_1} { (1 - \omega_1)} · (\mu_1 - \mu_0)^2 $。

　　4、将最大类间方差对应的灰度设置为阈值，并进行二值化。

　　

 

 算法原理

 　　

　　为了表述的方便，这里先定义一些符号：

	像素数占总图像的比例	平均灰度	类间方差
背景	$\omega_1$	$\mu_1$
前景	$\omega_2$	$\mu_2$
图像	$\omega_0$	$\mu_0$	$\sigma^2 $

 

　　类间方差指的是前景和背景之间的差异，显然该差异越大，说明分离度越好。数学上，类间方差的计算方法是：

$\sigma^2 = \omega_1 · (\mu_1 - \mu_0)^2 + \omega_2 · (\mu_2 - \mu_0)^2$（式2-1）

　　但直接采用该公式进行编程，不免有些繁杂，因此需要先进行一定的化简。将（式2-1）展开得：

$\sigma^2 = \omega_1 · \mu_1^2 + \omega_2 · \mu_2^2 - 2( \omega_1 · \mu_1 + \omega_2 · \mu_2)· \mu_0 + \mu_0^2 $（式2-2）

　　根据期望的数学定义式$E(X)=\sum_{k=1 }^{\infty}x_k·p_k$我们可以推知：

$\mu_0 = \omega_1 · \mu_1 + \omega_2 · \mu_2 $（式2-3）

　　将（式2-3）代入到（式2-2）中，则$\sigma^2 = \omega_1 · \mu_1^2 + \omega_2 · \mu_2^2 - \mu_0^2 $。然后我们希望可以把前景的成分消除掉，因此再次利用（式2-3）和$\omega_2 = 1 - \omega_1$的关系进行替换：

　　　　　　　　$\sigma^2 = \omega_1 · \mu_1^2 + \frac{\omega_2^2 · \mu_2^2}{1 - \omega_1} - \mu_0^2  = \omega_1 · \mu_1^2 + \frac{(\mu_0 -  \omega_1 · \mu_1)^2}{1 - \omega_1} - \mu_0^2  = \frac{\omega_1} { (1 - \omega_1)} · (\mu_1 - \mu_0)^2$（式2-4）

 　　使用（式2-4），我们就只需要统计当前迭代灰度以前的像素即可，这大大提升了程序的效率。此外，类间方差的最大点往往处于直方图的低谷处（如下图所示，红色点代表方差值），因此可以比较好地自动进行前景和背景分离。

　　

 

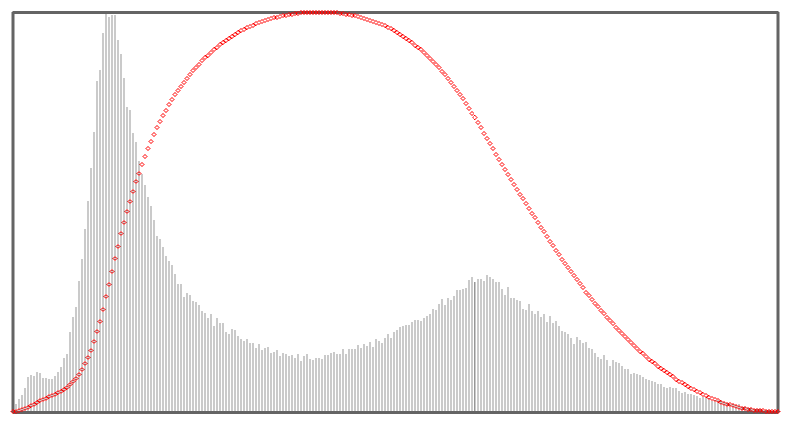
 算法复现

　复现需要注意的一点是背景平均灰度的计算，用公式可以表示为：

　　$\mu_1 = \frac{ \sum_{i=0}^{T} i · p_i}{ \sum_{i=0}^{T} p_i}$

　其中$i$表示迭代灰度，$p_i$表示$i$灰度级的比例，$T$为当前迭代灰度值。

unsigned char Ostu(int size,unsigned char *image)
{
    int i;
    unsigned char threshold=0;                        //阈值
    float variance=0;                                 //类间方差
    float maxvariance=0;                              //最大方差
    float k=0;                                    
    float w1=0;                                       //背景像素比例
    float u1=0;                                       //背景平均灰度
    float u0=0;                                       //图像的平均灰度
    float histogram[256]={0};                         //直方图

    for (i=0;i<size;i++){
        histogram[*(image+i)]++;                      //像素直方图
    }

    for (i=0;i<256;i++){
        histogram[i]/=size;                           //比例直方图
        u0+=histogram[i]*i;                           //计算图像平均灰度
    }

    for (i=0;i<256;i++){
        w1+=histogram[i];                             //背景比例
        k+=i*histogram[i];                        
        u1=k/w1;                                    　//背景平均灰度
        variance=w1/(1-w1)*(u1-u0)*(u1-u0);           //求方差
        if (variance>maxvariance){
            maxvariance=variance; 
            threshold=i;                              //将最大g相应的i值作为图像的全局阈值
        }        
    }

    return threshold;
}