AI 学习笔记

合集 - DL(1)

1.AI 学习笔记2023-05-05

AI 学习笔记

机器学习简介

Different types of Functions

Regression : The function outputs a scalar(标量）.

predict the PM2.5

Classification ： Given options (classes), the function outputs the correct one.

Spam filtering

Structured Learning ： create something with structure(image, document)

Example : YouTube Channel

1.Function with Unknown Parameters.

y = b + w x_{1}

$y=b+wx_1$

2.Define Loss from Training Data

Loss is a function of parameters

L (b, w)

$L(b,w)$

Loss : how good a set of values is.
L is mean absolute error (MAE)

e = | y - \hat{y} |

$e=\left | y-\hat{y} \right |$

L is mean square error (MSE)

e = (y - \hat{y})^{2}

$e=(y-\hat{y})^2$

L = \frac{1}{N} \sum_{n}^{} e_{n}

$L=\frac{1}{N} \sum_{n}^{}e_n$

3.Optimization

w^{*}, b^{*} = a r g min_{w, b} L

$w^*,b^*=arg\,\min_{w,b} \,L$

Gradient Descent

(Randomly) Pick an initial value ：

w^{0}

$w^0$

Compute :

\frac{\partial L}{\partial w} |_{w = w_{0}}

$\frac {\partial L} {\partial w} |_{w=w_0}$

Negative : Increase w

Positive : Decrease w

η \frac{\partial L}{\partial w} |_{w = w_{0}}

$\eta\frac {\partial L} {\partial w} |_{w=w_0}$

η：learning rate (hyperparameters)

Update w iteratively
- Local minima
- global minima

类似一个参数，推广到多个参数。

Linear Models

Linear models have severe limitation. Model Bias.

We need a more flexible model!

curve = constant + sum of a set of Hard Sigmoid Function

y = c \frac{1}{1 + e x p (- (b + w x_{1}))} = c s i g m o i d (b + w x_{1})

$y=c\frac {1} {1+exp(-(b+wx_1))} \\ =csigmoid(b+wx_1)$

y = b + \sum_{i} s i g m o i d (b_{i} + w_{i} x_{i})

$y=b+\sum_{i}sigmoid(b_i+w_ix_i)$

y = b + \sum_{i} s i g m o i d (b_{i} + \sum_{j} w_{i j} x_{j})

$y=b+\sum_{i}sigmoid(b_i+\sum_{j}w_{ij}x_j)$

线性代数角度：

r = b + W x

$r=b+Wx$

a = σ (r)

$a=\sigma(r)$

y = b + c^{T} a

$y=b+c^Ta$

Loss

Loss is a function of parameters L(θ)
Loss means how good a set of values is.

Optimization of New Model

θ = [\begin{matrix} θ_{1} \\ θ_{2} \\ θ_{3} \\ \dots \end{matrix}]

$\theta= \begin{bmatrix} \theta_1 \\ \theta_2 \\ \theta_3 \\ \dots \end{bmatrix}$

θ = a r g min_{θ} L

$\theta=arg \min_\theta L$

(Randomly) Pick initial values θ^0

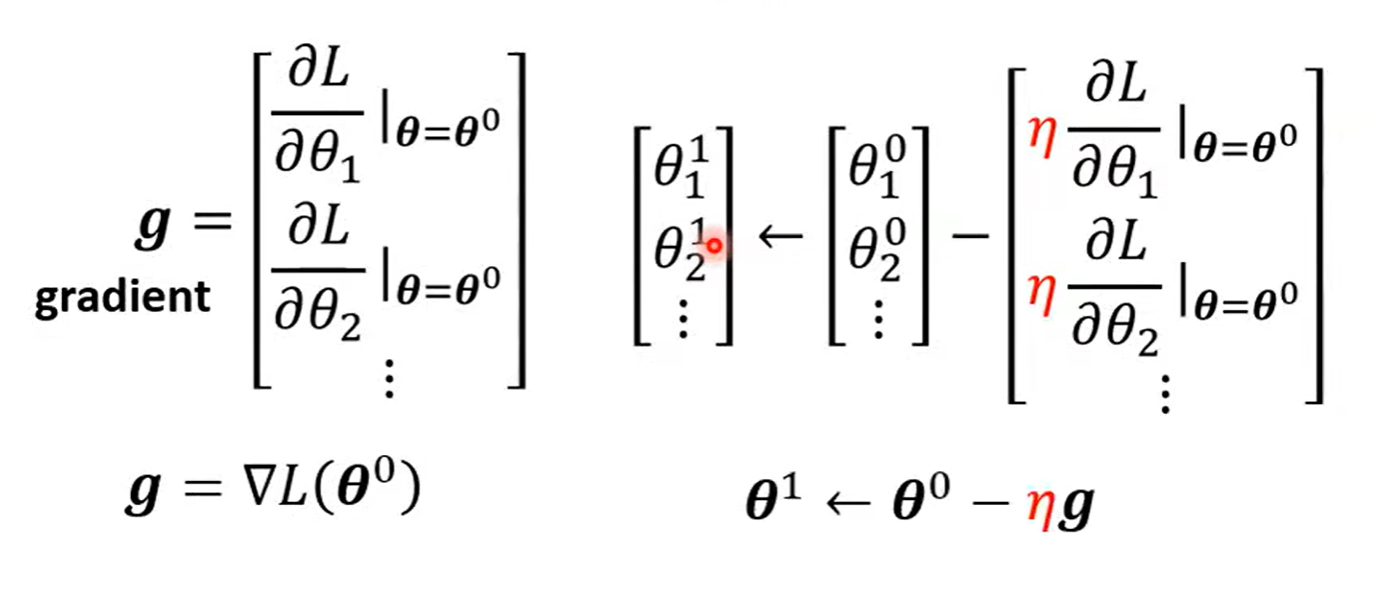
1 epoch = see all the batched once

update : update θ for each batch

Sigmoid -> ReLU (Rectified Linear Unit)

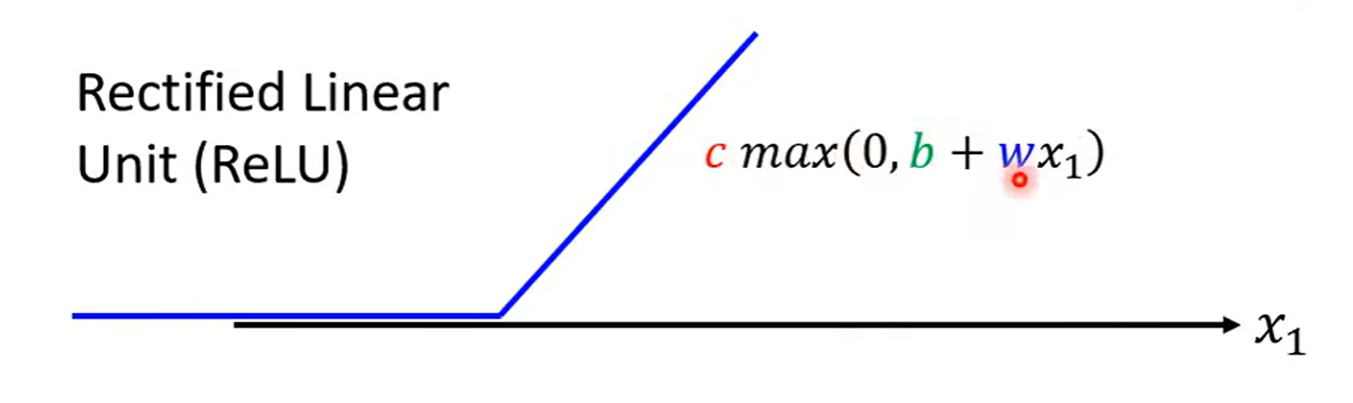
统称为 Activation function

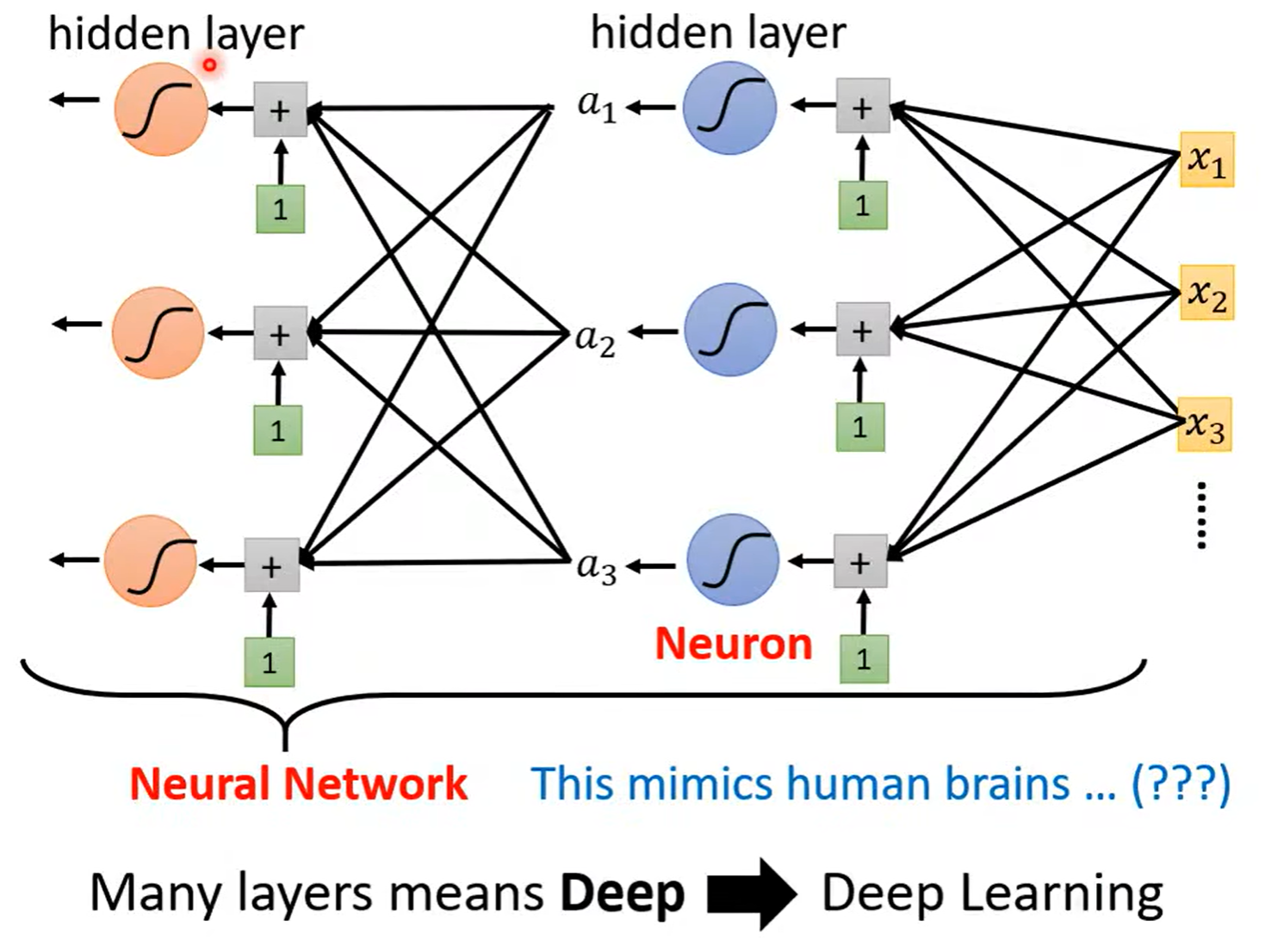
Neural Network

PyTorch

Python3中机器学习框架

 dataset = MyDataset(file)
dataloader = DataLoader(dataset, batch_size = size , shuffle = True)
Training : True
Testing : False

 from torch.utils.data import Dataset, DateLoader
class MyDataset(Dataset):
	def __init__(self, file): # read data & preprocess
		self.data = ...
	def __getitem__(self,index): #return one sample at a time
		return self.data[index]
	def __len__(self): #return the size of the dataset
		return len(self.data)

Tersors

High-dimensional matrices(arrays)

 .shape() # show the dimension
#Directly from data (list or numpy.ndarray)
x = torch.tensor([1, -1], [-1, 1])
x = torch.from_numpy(np.array([[1, -1], [-1, 1]]))
#Tensor of constant zeros & ones 
x = torch.zeros([2, 2])
x = torch.ones([1, 2, 5])
x+y x-y y=x.pow(2) y=x.sum() y=x.mean()
#Transpose : transpose two specified dimensions
x = x.transpose(dim0,dim1) # change the dimension dim0 and dim1
#Squeeze : remove the specified dimension with length 1 
x = x.squeeze(1)
#unsqueeze expand a new dimension
x = x.unsqueeze(1)

PyTorch

 dataset = MyDataset(file)
dataloader = Dataloader(dataset, batch_size, shuffle = True)
shuffle : Training -> true
		  Testing -> false

Tersors

High-dimensional matrices(matrix used in mathematics, arrays)

dim in PyTorch == axis in NumPy

dimensional

 Check with.shape()

Creating Tensors

Directly from data (list or numpy.ndarray)

 x = torch.tensor([1, -1], [-1, 1])
x = torch.from_numpy(np.array([[1, -1], [-1, 1]]))

Tensor of constant zeros & ones

 x = torch.zeros([2,2])
x = torch.ones([1, 2, 5])

Common Operations

addition subtraction power summation mean

transpose

 x.shape
x.transpose(0,1)

Unsqueeze : expand a new dimension

 x = x.unsqueeze(1)

**Cat **: conncatenate multiple tensors 合并多个矩阵

 torch.cat([x, y, z], dim = 1)

Data Type: Using different data types for model and data will case errors.

32-bit -torch.float

64-bit -torch.long

Device

Tensors & modules will be computed with CPU by default
Use .to() to move tensors to appropriate devices
- CPU
  - x = x.to('cpu') - ```py x = x.to('cuda')
GPU
- check if your computer has NVIDIA GPU
  - torch.cuda.is_available() - Multiple GPUs : specify- ``` 'cuda:0', 'cuda:1', 'cuda:2',...

Cradient Calculation

 import torch
# 定义一个需要求导的张量 x，并将 requires_grad 参数设置为 True 
x = torch.tensor([[1., 0.], [-1., 1.]], requires_grad=True)
# 计算 x 的平方并对其进行求和，得到张量 z
z = x.pow(2).sum()
# 对张量 z 进行反向传播，自动计算出 x 的梯度
z.backward()
# 输出 x 的梯度
print(x.grad)

torch.nn

Network Layers

Linear Layer (Fully-connected Layer)
- nn.linear(in_features, out_features) #### Non-linear Activation Functions```pynn.Sigmoid()nn.ReLU()

Build your own neural network

 import torch.nn as nn
class MyModel(nn.Module):
    #initialize your model & define layers
	def __init__(self):
		super(MyModel, self).__init__()
		self.net = nn.Sequential(
			nn.Linear(10, 32),
			nn.Sigmoid(),
			nn.Linear(32,1)
		)
	#compute output of your nn
	def forward(self, x):
		return self.next()

Loss Functions

Mean squared Error (for regression tasks)

 criterion = nn.MSELoss()

Cross Entropy (for classification tasks) 交叉熵

 criterion = nn.CrossEntropyLoss()

loss = criterion(model_output, expected_value) ### torch.optim- Stochastic Gradient Descent (SGD) - ```py torch.optim.SGD(model.parameters(), lr, momentum = 0)
For every batch of data
- Call optimizer.zero_grad() to reset gradients of model parameters.
- Call loss.backward() to backpropagate gradients of prediction loss
- Call optimizer.step() to adjust model parameters

Neural Network Training Setup

 dataset = MyDataSet(file)
tr_set = DataLoader(dataset, 16, shuffle = True)
model = MyModel().to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), 0.1)

Training Loop

 for epoch in range(n_epochs):  # Iterate over n_epochs
    model.train()  # Set the model to training mode
    for x, y in tr_set:  # Iterate over the training set
        optimizer.zero_grad()  # Clear the gradients
        x, y = x.to(device), y.to(device)  # Move data to the device (e.g., GPU)
        pred = model(x)  # Forward pass, compute predictions
        loss = criterion(pred, y)  # Compute the loss
        loss.backward()  # Backward pass, compute gradients
        optimizer.step()  # Update the model's parameters using the gradients

Validation Loop

 model.eval()  # Set the model to evaluation mode
total_loss = 0
 
for x, y in dv_set:  # Iterate over the validation set
    x, y = x.to(device), y.to(device)  # Move data to the device
    with torch.no_grad():  # Disable gradient computation
        pred = model(x)  # Forward pass, compute predictions
        loss = criterion(pred, y)  # Compute the loss
    total_loss += loss.cpu().item() * len(x)  # Accumulate the loss
avg_loss = total_loss / len(dv_set)  # Calculate the average loss per sample

Testing Loop

 model.eval()  # Set the model to evaluation mode
preds = []
 
for x in tt_set:  # Iterate over the test set
    x = x.to(device)  # Move data to the device
    with torch.no_grad():  # Disable gradient computation
        pred = model(x)  # Forward pass, compute predictions
        preds.append(pred.cpu())  # Append the predictions to the list

Data, demo1

Load data :

use pandas to load a csv file

 train_data = pd.read_cav('./name.csv').drop(columns=['date']).values
x_train, y_train = train_data[:,:-1], train_data[:,:-1]

Dataset

init : Read data and preproces

getitem : Return one sample at a time, In this case, one sample includes a 117 dimensional feature and a label

len : Return the size of the dataset. In this case, it is 2699

 class COVID19Dataset(Dataset):
    '''
    x: np.ndarray  特征矩阵.
    y: np.ndarray  目标标签, 如果为None,则是预测的数据集
    '''
    def __init__(self, x, y=None):
        if y is None:
            self.y = y
        else:
            self.y = torch.FloatTensor(y)
        self.x = torch.FloatTensor(x)
 
    def __getitem__(self, idx):
        if self.y is None:
            return self.x[idx]
        return self.x[idx], self.y[idx]
 
    def __len__(self):
        return len(self.x)

Dataloader

 train_loader = DataLoader(train_dataset, batch_size = 32, shuffle = True, pin_memory = True)

Model

 class My_Model(nn.Module):
    def __init__(self, input_dim):
        super(My_Model, self).__init__()
        # TODO: 修改模型结构, 注意矩阵的维度（dimensions） 
        self.layers = nn.Sequential(
            nn.Linear(input_dim, 16),
            nn.ReLU(),
            nn.Linear(16, 8),
            nn.ReLU(),
            nn.Linear(8, 1)
        )
 
    def forward(self, x):
        x = self.layers(x)
        x = x.squeeze(1) # (B, 1) -> (B)
        return x

Criterion

 criterion = torch.nn.MSELoss(reduction = 'mean')

Optimizer

 optimizer = torch.optim.SGD(model.parameters(), lr = 1e-5, momentum = 0.9)

Training Loop

Documentation and Common Errors

read pytorch tutorial

Colab（highly recommended）

Officially begin

Deep = Many hidden layers

Neurall Network

Find a function in function set.

Goodness of function

Pick the best function

Backpropagation - Backward Pass(反向传播)

反向的neural network

Regression

Stock Market Forecast
Self-driving Car
Recommendation

Step 1 : Model

A set of function

Step 2 : Goodness of Function

{\hat{y}}^{1} 代 表 x^{1} 对 应 的 确 切 值

$\hat{y}^1代表x^1对应的确切值$

Loss function L：

L (f) = L (w, b) E s t i m a t e d y b a s e d o n i n p u t f u n c t i o n

$L(f)=L(w,b) ~ Estimated ~ y ~ based~~oninput~~function$

L (w, b) = \sum_{n = 1}^{10} ({\hat{y}}^{n} - (b + w \cdot x_{c p}^{n}))^{2}

$L(w,b)=\sum_{n=1}^{10}(\hat{y}^n-(b+w\cdot x_{cp}^n))^2$

Step 3 ：Best Function

In linear regression, the loss function L is convex.

Overfitting

Regularization

L (w, b) = \sum_{n = 1}^{10} ({\hat{y}}^{n} - (b + w \cdot x_{c p}^{n}))^{2} + λ \cdot \sum (w_{i})^{2}

$L(w,b)=\sum_{n=1}^{10}(\hat{y}^n-(b+w\cdot x_{cp}^n))^2+\lambda\cdot \sum(w_i)^2$

不需要考虑bias，调整平滑程度，smooth

Gradient descent
Overfitting and Regularization

Classification

Training data for Classification

pair

Ideal Alternatives

Function(Model):

f (x) x - > g (x) > 0 O u t p u t = c l a s s 1 e l s e O u t p u t = c l a s s 2

$f(x)\\ x -> g(x)>0~Output=class1 else Output=class2$

lossfunction:

The number of times of get incotrrect results on training data.

L (f) = \sum_{n} δ (f (x^{n}) \neq {\hat{y}}^{n})

$L(f) = \sum_{n}\delta(f(x^n)\neq\hat{y}^n)$

Find the best function;

Example : Perceptron, SVM

Prior

P (C_{1} | x) = \frac{P (x | C_{1}) P (C_{1})}{P (x | C_{1}) P (C_{1}) + P (x | C_{2}) P (C_{2})}

$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$

Gaussian

Maximum Likelihood

2D array or 3D array mean the array with 2 or 3 axes respectively, but the n-dimensional vector mean the vector of length n.

Learn something that can really differ you from others.

posted @ 2023-05-05 11:59 Kennems 阅读(66) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· AcWing

· 数据库学习笔记

· 李宏毅机器学习笔记:从0到写AI

· AI入门之深度学习：基本概念篇

· 深度学习（十三）——损失函数与反向传播

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

阅读目录(Content)

AI 学习笔记

机器学习简介

Linear Models
Optimization of New Model
Sigmoid -> ReLU (Rectified Linear Unit)

Classification

Training data for Classification
Ideal Alternatives

Prior
Gaussian

	dataset = MyDataset(file)
	dataloader = DataLoader(dataset, batch_size = size , shuffle = True)
	Training : True
	Testing : False

	from torch.utils.data import Dataset, DateLoader
	class MyDataset(Dataset):
	def __init__(self, file): # read data & preprocess
	self.data = ...
	def __getitem__(self,index): #return one sample at a time
	return self.data[index]
	def __len__(self): #return the size of the dataset
	return len(self.data)

	.shape() # show the dimension
	#Directly from data (list or numpy.ndarray)
	x = torch.tensor([1, -1], [-1, 1])
	x = torch.from_numpy(np.array([[1, -1], [-1, 1]]))
	#Tensor of constant zeros & ones
	x = torch.zeros([2, 2])
	x = torch.ones([1, 2, 5])
	x+y x-y y=x.pow(2) y=x.sum() y=x.mean()
	#Transpose : transpose two specified dimensions
	x = x.transpose(dim0,dim1) # change the dimension dim0 and dim1
	#Squeeze : remove the specified dimension with length 1
	x = x.squeeze(1)
	#unsqueeze expand a new dimension
	x = x.unsqueeze(1)

	dataset = MyDataset(file)
	dataloader = Dataloader(dataset, batch_size, shuffle = True)
	shuffle : Training -> true
	Testing -> false

	import torch
	# 定义一个需要求导的张量 x，并将 requires_grad 参数设置为 True
	x = torch.tensor([[1., 0.], [-1., 1.]], requires_grad=True)
	# 计算 x 的平方并对其进行求和，得到张量 z
	z = x.pow(2).sum()
	# 对张量 z 进行反向传播，自动计算出 x 的梯度
	z.backward()
	# 输出 x 的梯度
	print(x.grad)

	import torch.nn as nn
	class MyModel(nn.Module):
	#initialize your model & define layers
	def __init__(self):
	super(MyModel, self).__init__()
	self.net = nn.Sequential(
	nn.Linear(10, 32),
	nn.Sigmoid(),
	nn.Linear(32,1)
	)
	#compute output of your nn
	def forward(self, x):
	return self.next()

	dataset = MyDataSet(file)
	tr_set = DataLoader(dataset, 16, shuffle = True)
	model = MyModel().to(device)
	criterion = nn.MSELoss()
	optimizer = torch.optim.SGD(model.parameters(), 0.1)

	for epoch in range(n_epochs): # Iterate over n_epochs
	model.train() # Set the model to training mode
	for x, y in tr_set: # Iterate over the training set
	optimizer.zero_grad() # Clear the gradients
	x, y = x.to(device), y.to(device) # Move data to the device (e.g., GPU)
	pred = model(x) # Forward pass, compute predictions
	loss = criterion(pred, y) # Compute the loss
	loss.backward() # Backward pass, compute gradients
	optimizer.step() # Update the model's parameters using the gradients

	model.eval() # Set the model to evaluation mode
	total_loss = 0

	for x, y in dv_set: # Iterate over the validation set
	x, y = x.to(device), y.to(device) # Move data to the device
	with torch.no_grad(): # Disable gradient computation
	pred = model(x) # Forward pass, compute predictions
	loss = criterion(pred, y) # Compute the loss
	total_loss += loss.cpu().item() * len(x) # Accumulate the loss
	avg_loss = total_loss / len(dv_set) # Calculate the average loss per sample

	model.eval() # Set the model to evaluation mode
	preds = []

	for x in tt_set: # Iterate over the test set
	x = x.to(device) # Move data to the device
	with torch.no_grad(): # Disable gradient computation
	pred = model(x) # Forward pass, compute predictions
	preds.append(pred.cpu()) # Append the predictions to the list

	train_data = pd.read_cav('./name.csv').drop(columns=['date']).values
	x_train, y_train = train_data[:,:-1], train_data[:,:-1]

	class COVID19Dataset(Dataset):
	'''
	x: np.ndarray 特征矩阵.
	y: np.ndarray 目标标签, 如果为None,则是预测的数据集
	'''
	def __init__(self, x, y=None):
	if y is None:
	self.y = y
	else:
	self.y = torch.FloatTensor(y)
	self.x = torch.FloatTensor(x)

	def __getitem__(self, idx):
	if self.y is None:
	return self.x[idx]
	return self.x[idx], self.y[idx]

	def __len__(self):
	return len(self.x)

	class My_Model(nn.Module):
	def __init__(self, input_dim):
	super(My_Model, self).__init__()
	# TODO: 修改模型结构, 注意矩阵的维度（dimensions）
	self.layers = nn.Sequential(
	nn.Linear(input_dim, 16),
	nn.ReLU(),
	nn.Linear(16, 8),
	nn.ReLU(),
	nn.Linear(8, 1)
	)

	def forward(self, x):
	x = self.layers(x)
	x = x.squeeze(1) # (B, 1) -> (B)
	return x

🌞

有朝一日，太阳降临。

念两句诗

AI 学习笔记

AI 学习笔记

机器学习简介

1.Function with Unknown Parameters.

2.Define Loss from Training Data

3.Optimization

Linear Models

Optimization of New Model

Sigmoid -> ReLU (Rectified Linear Unit)

PyTorch

Tersors

PyTorch

Tersors

Creating Tensors

Cradient Calculation

torch.nn

Network Layers

Build your own neural network

Loss Functions

Neural Network Training Setup

Training Loop

Validation Loop

Testing Loop

Data, demo1

Load data :

Dataset

Dataloader

Model

Criterion

Optimizer

Training Loop

Documentation and Common Errors

Colab（highly recommended）

Officially begin

Neurall Network

Goodness of function

Backpropagation - Backward Pass(反向传播)

Regression

Step 1 : Model

Step 2 : Goodness of Function

Step 3 ：Best Function

Regularization

Classification

Training data for Classification

Ideal Alternatives

Function(Model):

lossfunction:

Find the best function;

Prior

Gaussian

公告

个人信息

日历

搜索

常用链接

最新随笔

我的标签

积分与排名

合集 (1)

随笔档案 (12)

相册 (1)

阅读排行榜

评论排行榜

最新评论