5.1二维图形变化
一、向量
是具有长度和方向的实体
二、特殊的线性组合
（1）仿射组合
（2）凸组合（对仿射组合加以更多的限制）
三、向量的点积和叉积
（1）点积
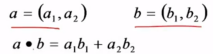
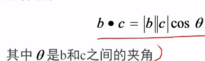两个向量夹角的余弦值等于两个单位向量的点积
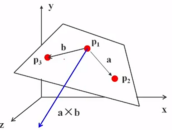
（2）叉积
两个向量的叉积是另一个三维向量，且与两个向量均正交
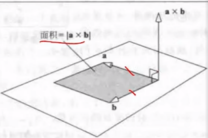
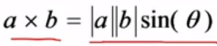
利用叉积求平面的法向量，三点可确定一个平面
5.2 图形坐标系
1、世界坐标系
是一个公共坐标系，是现实中物体或场景的统一参考系
2、建模坐标系
又称局部坐标系，每个物体有自己的局部中心和坐标系
3、观察坐标系
从观察者的角度对世界坐标系内的对象进行重新定位
4、设备坐标系
适合特定输出设备输出对象的坐标系，例如：屏幕坐标系。注意：设备坐标是整数。
5、规范化坐标系
为使图形软件能在不同的设备之间移植，是一个中间坐标系，坐标轴取值范围是0-1。
5.3 二维图形变换原理及齐次坐标
1、图形变换的用途：一个简单的图形，通过各种变换（比例、旋转、镜像、错切、平移等）可以形成一个丰富多彩的图形。
2、图形变换的基本原理：
（1）图形变换了，但原图形的连边规则没有改变
（2）图形的变换，是因为顶点位置的改变决定的
3、仿射变换：是一种二维坐标到二维坐标的线性变换
（1）平直性。直线变换后仍然是直线
（2）平行性。平行线变换后仍然是平行线
4、齐次坐标
M为变换矩阵
这种用n+1维的向量表示n维向量的方法称为齐次坐标表示法
在笛卡尔坐标系内，向量（x,y）是位于z=0的平面上的点；而向量(x,y,1)是位于z=1的等高平面上的点
5.4 二维图形几何变换
图形的几何变换是指对图形的几何信息进行平移、比例、旋转等变换后产生新的图形。
一、平移变换
平移是指将P点沿直线路径从一个坐标位置移到另一个坐标位置的重定位过程。
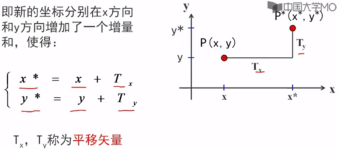
矩阵形式为：
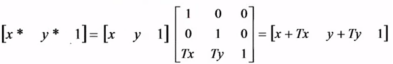
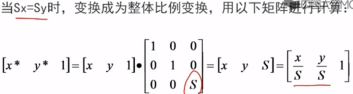
二、比例变换
是指对P点相对于坐标原点沿x方向放缩Sx倍，沿y方向放缩Sy倍。其中Sx和Sy称为比例系数。
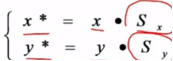
Sx和Sy可相等可不相等
齐次坐标计算形式如下：
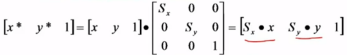
若s<0,发生关于原点的对称等比变换
三、对称变换
也称为反射变换或镜像变换，变换后的图形是原图形关于某一轴线或原点的镜像。
1>关于x轴对称
2>关于y轴对称
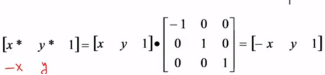
四、旋转变换
指将P点绕坐标原点转动某个角度θ（逆时针为正，顺时针为负）得到新的点
顺时针旋转吧θ变成-θ，再化简即可
五、错切变换
符合刚性变换（仿射变换）：直线/平行线变换以后仍然是直线/平行线
1>沿x方向错切，y不变，所以b=0
2>沿y方向错切，x不变，所以c=0
为什么要用齐次坐标？
比例、对称、旋转均可用二维变换矩阵表示，但是对于平移来说，用二维表示不出来，只能用三维，所以为了统一形式，都用齐次坐标表示
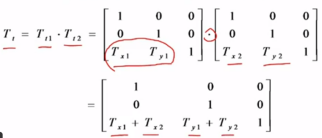
六、复合变换
是指图形作一次以上的几何变换，变换结果是每次的变换矩阵相乘
1>二维复合平移（平移量相加）
2>二维复合比例平移（比例量相乘）
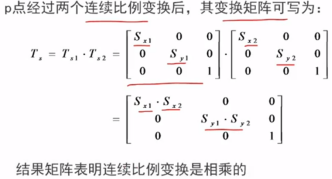
3>二维复合旋转（旋转角度相加）
复合变换时，注意矩阵相乘的顺序！！！
七、坐标系之间的变换
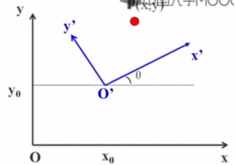
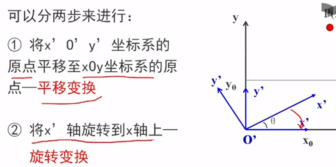
上述步骤可用变换矩阵表示：
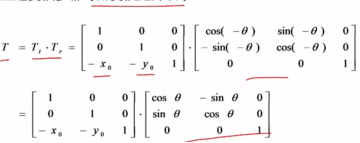注意负号！！！
八、相对任意参考点的二维几何变换
若对某个参考点(x,y)做变换，其变换过程如下：
1>将固定点移至坐标原点，此时进行平移变换
2>针对原点进行二维几何变换
3>进行反平移，将固定点又移到原来的位置
九、二维变换矩阵
1、
投影变换在三维图形中重要
2、直线的变换
可以通过对直线两端点进行变换，然后连线，从而改变直线的位置和方向
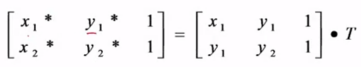
3、多边形的变换
将多边形的顶点进行变换，然后连线
5.5 窗口视区变换
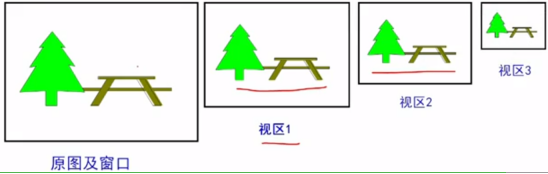
一、窗口和视区
世界坐标系中要显示的区域，称为窗口
窗口映射到显示器上（设备）上的区域称为视区
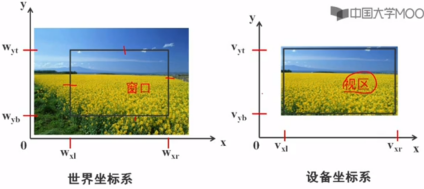
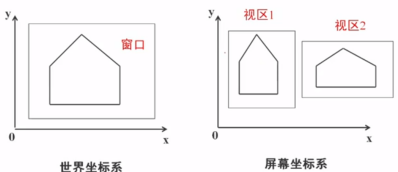
世界坐标系中的一个窗口可以对应多个视区
二、观察变换
1、变焦距效果
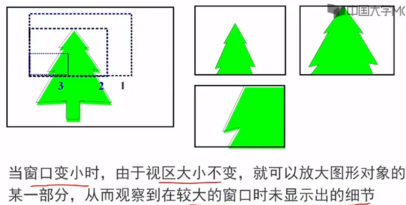
当窗口变大，视区不变时，图像会变小，这类似于照相机的变焦原理
2、整体缩放效果
当窗口大小不变而视区大小发生变化时，得到整体的缩放效果，这种放缩不改变观察对象的内容。
三、窗口到视区的映射
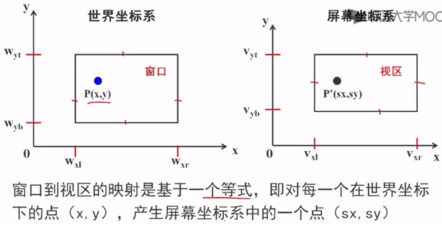
这个映射是保持比例的映射，这个性质使得这个映射有线性性质：
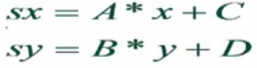，其中a,b,c,d是常数
推导过程：
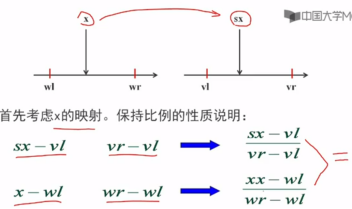
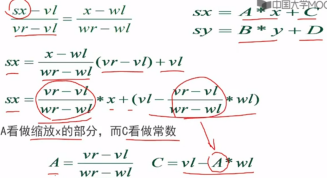
这个映射可用于任意点(x,y),不管它是否在窗口内。在窗口中的点映射到视区中的点，窗口外的点映射到视区外的点。
5.6 二维几何变换小结
主要讲述向量的基本知识、坐标系的分类、齐次坐标、二维变换等、窗口与视区
