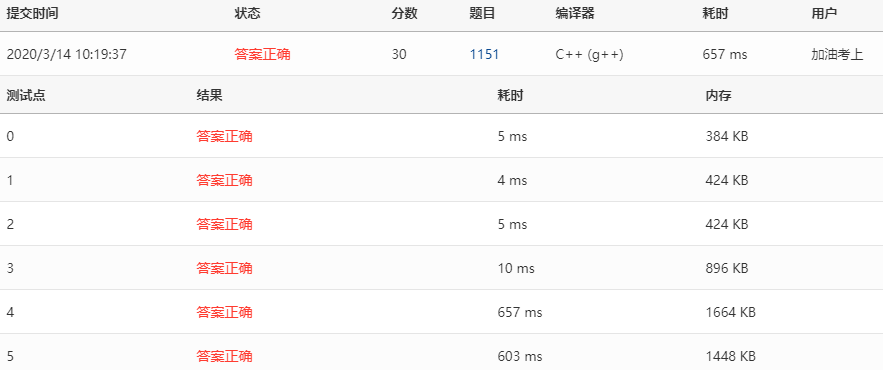
1151 LCA in a Binary Tree(两结点的最近公共祖先)
好难啊!!!自己做是一个错误,加两个超时,呜呜呜。。。
大致题意就是给出一棵树的先序、中序遍历序列,可以构造一棵树。然后给两个顶点,找出这两个结点的最近公共祖先。
思路分析:
1,什么是最近公共祖先?就是说给定 树中两个结点u,v,一定能找到一个且只能找到一个结点root,使得
情况一,root的左子树是u(或者v),右子树是v(或者u)。
情况二,root本身是u(或者v),root的左子树或者右子树包含v(或者u)。
情况三,root既是u也是v。(测试点2)
2,因为题中给出了树的中序、先序遍历序列,所以本可以 以此构造一棵树,但实际上不用建树(如果充分理解建树过程),因为在建树过程中是可以实现(先序、中序、后序)遍历操作的,所以我们可以借助 (先序、中序、后序)遍历获得每层的根结点和上面的思路分析 1 来查找最近公共祖先。
最开始代码,其中遍历左、右子树操作,以及查找结点是否在二叉树中 这三个顺序遍历操作,导致测试点4,5超时;一个u==v的情况未考虑导致测试点2答案错误。
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 const int maxn = 10010; 5 int m,n,pre[maxn],in[maxn],u,v,flag1,flag2; 6 7 //先序+中序 = 二叉树 8 void create(int preL,int preR,int inL,int inR) {//可以在建树过程中(实际并没有建树),根据后序遍历来查找最近公共祖先 9 if(inL > inR) return ; 10 int k,leftNum; 11 for(k = inL; k < inR; ++k) 12 if(in[k] == pre[preL]) break; 13 leftNum = k-inL; 14 create(preL+1,preL+leftNum,inL,k-1); 15 create(preL+leftNum+1,preR,k+1,inR); 16 int L = -1 ,R = -1; 17 for(int i = inL; i <= k-1; ++i) //遍历左子树,两个遍历操作导致超时 18 if(in[i] == u || in[i] == v) L = i; 19 for(int i = k+1; i <= inR; ++i)//遍历右子树 20 if(in[i] == u || in[i] == v) R = i; 21 if(L != -1 && R != -1)//情况一 22 printf("LCA of %d and %d is %d.\n",u,v,in[k]); 23 if((L != -1||R != -1)&&(in[k] == u||in[k] == v)) //情况二 24 printf("%d is an ancestor of %d.\n",in[k],in[L!=-1?L:R]); 25 } 26 27 int main() { 28 cin>>m>>n; 29 for(int i = 0; i < n; ++i) scanf("%d",&in[i]); 30 for(int i = 0; i < n; ++i) scanf("%d",&pre[i]); 31 for(int i = 0; i < m; ++i) { 32 scanf("%d%d",&u,&v); 33 flag1 = flag2 = 1; 34 for(int j = 0; j < n && (flag1 || flag2); ++j) { //顺序遍历,超找结点是否在树中 35 if(u == in[j]) flag1 = 0; 36 if(v == in[j]) flag2 = 0; 37 } 38 if(flag1 && flag2) printf("ERROR: %d and %d are not found.\n",u,v); 39 else if(flag1) printf("ERROR: %d is not found.\n",u); 40 else if(flag2) printf("ERROR: %d is not found.\n",v); 41 else { 42 if(u == v) printf("%d is an ancestor of %d.\n",u,v);//,必须特判。不然测试点2过不去 43 else create(0,n-1,0,n-1); 44 } 45 } 46 return 0; 47 }

改用map记录中序遍历序列各个结点的位置下标,解决顺序遍历导致超时的问题。
1 #include<iostream> 2 #include<unordered_map> 3 #include<algorithm> 4 using namespace std; 5 const int maxn = 10010; 6 int m,n,pre[maxn],in[maxn],u,v,flag; 7 unordered_map<int,int> pos; //记录结点在中序遍历序列的下标 8 9 void LCA(int preL,int preR,int inL,int inR) { 10 if(inL > inR) return ; 11 int k = pos[pre[preL]],inU = pos[u],inV = pos[v]; 12 int leftNum = k-inL; 13 LCA(preL+1,preL+leftNum,inL,k-1); 14 LCA(preL+leftNum+1,preR,k+1,inR); 15 if(((inL <= inU&&inU < k)&&(k < inV&&inV<=inR))||(inL <= inV&&inV < k)&&(k < inU&&inU<=inR)) //情况一 16 printf("LCA of %d and %d is %d.\n",u,v,in[k]); 17 else if(inU == k&&((inL<=inV&&inV < k)||(k < inV&&inV<=inR)))//情况二 18 printf("%d is an ancestor of %d.\n",u,v); 19 else if(inV == k&&((inL<=inU&&inU < k)||(k < inU&&inU<=inR)))//情况二 20 printf("%d is an ancestor of %d.\n",v,u); 21 } 22 23 int main() { 24 cin>>m>>n; 25 for(int i = 1; i <= n; ++i) scanf("%d",&in[i]),pos[in[i]] = i; 26 for(int i = 1; i <= n; ++i) scanf("%d",&pre[i]); 27 for(int i = 0; i < m; ++i) { 28 scanf("%d%d",&u,&v); 29 if(pos[u] == 0 && pos[v] == 0) printf("ERROR: %d and %d are not found.\n",u,v); 30 else if(pos[u] == 0||pos[v] == 0) printf("ERROR: %d is not found.\n",pos[u] == 0?u:v); 31 else { 32 if(u == v) printf("%d is an ancestor of %d.\n",u,v);//,必须特判。不然测试点2过不去 33 else LCA(1,n,1,n); 34 } 35 } 36 return 0; 37 }
参考刘婼的代码,思路如下:
不用建树~已知某个树的根结点,若a和b在根结点的左边,则a和b的近公共祖先在当前⼦子树 根结点的左⼦子树寻找,如果a和b在当前⼦子树根结点的两边,在当前⼦子树的根结点就是a和b的近公共 祖先,如果a和b在当前⼦子树根结点的右边,则a和b的近公共祖先就在当前⼦子树的右⼦子树寻找。中序 加先序可以唯⼀一确定⼀一棵树,在不不构建树的情况下,在每⼀一层的递归中,可以得到树的根结点,在此 时并⼊入lca算法可以确定两个结点的公共祖先~
1 #include<iostream> 2 #include<unordered_map> 3 #include<algorithm> 4 using namespace std; 5 const int maxn = 10010; 6 int m,n,pre[maxn],in[maxn],u,v,flag; 7 unordered_map<int,int> pos; 8 9 void LCA(int inL,int inR,int preRoot,int u,int v) { 10 if(inL > inR) return ; 11 int inRoot = pos[pre[preRoot]],inU = pos[u],inV = pos[v]; 12 if((inU < inRoot && inRoot < inV)||(inU > inRoot && inRoot > inV)) //情况一 13 printf("LCA of %d and %d is %d.\n",u,v,in[inRoot]); 14 else if(inU == inRoot)//情况二 15 printf("%d is an ancestor of %d.\n",u,v); 16 else if(inV == inRoot)//情况二 17 printf("%d is an ancestor of %d.\n",v,u); 18 else if(inU < inRoot && inV < inRoot) //遍历左子树 19 LCA(inL,inRoot-1,preRoot+1,u,v); 20 else if(inU > inRoot && inV > inRoot) //遍历右子树 21 LCA(inRoot+1,inR,preRoot+1+(inRoot-inL),u,v); 22 } 23 24 int main() { 25 cin>>m>>n; 26 for(int i = 1; i <= n; ++i) scanf("%d",&in[i]),pos[in[i]] = i; 27 for(int i = 1; i <= n; ++i) scanf("%d",&pre[i]); 28 for(int i = 0; i < m; ++i) { 29 scanf("%d%d",&u,&v); 30 if(pos[u] == 0 && pos[v] == 0) printf("ERROR: %d and %d are not found.\n",u,v); 31 else if(pos[u] == 0||pos[v] == 0) printf("ERROR: %d is not found.\n",pos[u] == 0?u:v); 32 else LCA(1,n,1,u,v); 33 } 34 return 0; 35 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号