层序+中序 = 二叉树

先序+中序 = 二叉树。

pre[n]存放先序序列，in[n]存放中序序列。

一，递归边界：中序序列的左边界必须小于等于右边界。

二，递归：

1，取当前先序序列[preL,preR]的第一个元素pre[preL]作为根节点root，

2，在当前中序序列中找出根节点root的下标k，把当前中序序列划分为[inL,k-1]，[k+1,inR]，分别是当前根节点root的左子树的中序序列，和右子树的中序序列。

3，根据左子树的结点个数，可以把当前先序序列划分成当前根节点root的左子树的先序序列，和右子树的先序序列。

结合步骤，直接看代码。

 1 //当前二叉树的 先序区间[preL,preR], 中序区间[inL,inR]
 2 Node* create(int preL,int preR,int inL,int inR) {
 3     //第一步，确定递归边界
 4     if(inL > inR)     return NULL;
 5     //第二步，保存当前根结点
 6     Node* root = new Node;
 7     root->data = pre[preL];
 8     //第三步，用根结点划分中序,求出根节点左子树结点的个数
 9     int k,leftNum;
10     for(k = inL; k <= inR; ++k)
11         if(in[k] == pre[preL]) break;
12     leftNum = k - inL;
13     //第四步，确定左子树的后序、中序， 右子树的后序，中序
14     root->lchild = create(preL+1,preL+leftNum,inL,k-1);//红色部分是先序序列，绿色部分是中序序列
15     root->rchild = create(preL+leftNum+1,preR,k+1,inR);
16     return root;
17 }

后序+中序 = 二叉树。

post[n]存放后序序列，in[n]存放中序序列。

一，递归边界：中序序列的左边界必须小于等于右边界。

二，递归：

1，取当前后序序列[postL,postR]的最后一个元素post[postR]作为根节点root，

3，根据左子树的结点个数，可以把当前后序序列划分成当前根节点root的左子树的后序序列，和右子树的后序序列。

结合步骤，直接看代码。

 1 //当前二叉树的 后序区间[postL,postR], 中序区间[inL,inR]
 2 Node* create(int postL,int postR,int inL,int inR) {
 3     //第一步，确定递归边界
 4     if(inL > inR) return NULL;
 5     //第二步，保存当前根结点
 6     Node* root = new Node;
 7     root->data = post[postR];
 8     //第三步，用根结点划分中序,求出根节点左子树结点的个数
 9     int k,leftNum;
10     for(k = inL; k <= inR; ++k)
11         if(in[k] == post[postR]) break;
12     leftNum = k - inL;
13     //第四步，确定左子树的后序、中序， 右子树的后序，中序
14     root->lchild = create(postL,postL+leftNum-1,inL,k-1);
15     root->rchild = create(postL+leftNum,postR-1,k+1,inR);
16     return root;
17 }

层序+中序 = 二叉树。

level[n]存放先序序列，in[n]存放中序序列。

一，递归边界：中序序列的左边界必须小于等于右边界。

二，递归：

1，找到当前层序序列中第一个出现在当前中序序列的元素作为根节点root，

结合步骤，直接看代码。

 1 //当前二叉树的 层序区间[levelL,levelR], 中序区间[inL,inR]
 2 Node* create(int levelL,int levelR,int inL,int inR) {
 3     //第一步，确定递归边界
 4     if(inL > inR) return NULL;
 5     //第二步，找到当前层序序列中 第一个 出现在当前中序序列的元素 作为根节点root
 6     Node* root = new Node;
 7     int k,flag = 0;
 8     for(  ; levelL <= levelR; ++levelL) {//当前层序序列[levelL,levelR]
 9         for(k = inL; k <= inR; ++k) {//当前中序序列 [inL,inR]
10             if(in[k] == level[levelL]) {
11                 flag = 1; //找到！ 
12                 break;
13             }
14         }
15         if(flag == 1) break;
16     }
17     root->data = level[levelL];
18     //第三步，确定当前根节点的左子树的层序序列 和中序序列，右子树的层序序列 和中序序列
19     root->lchild = create(levelL+1,levelR,inL,k-1);
20     root->rchild = create(levelL+1,levelR,k+1,inR);
21     return root; //总是忘记这个小可爱~~
22 }

输入样例：

7
4 1 6 3 5 7 2
1 2 3 4 5 6 7

输出样例：

4 1 3 2 6 5 7 //先序序列

直接上代码。。。

#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 100;

struct Node {
    int data;
    Node* lchild;
    Node* rchild;
};
int level[maxn],in[maxn];//层序、中序序列
int n;//结点个数

int num = 0;//已经访问的结点个数
void preorder(Node* root) { //先序遍历
    if(root == NULL) return ;
    if(num > 0) printf(" ");
    cout<<root->data;
    num++;
    preorder(root->lchild);//访问左子树，两个选择分支
    preorder(root->rchild);//访问右子树
}
//当前二叉树的 层序区间[levelL,levelR], 中序区间[inL,inR]
Node* create(int levelL,int levelR,int inL,int inR) {
    //第一步，确定递归边界
    if(inL > inR) return NULL;
     //第二步，找到当前层序序列中 第一个 出现在当前中序序列的元素 作为根节点root
    Node* root = new Node;
    int k,flag = 0;
    for(  ; levelL <= levelR; ++levelL) {//当前层序序列[levelL,levelR]
        for(k = inL; k <= inR; ++k) {//当前中序序列 [inL,inR]
            if(in[k] == level[levelL]) {
                flag = 1; //找到！ 
                break;
            }
        }
        if(flag == 1) break;
    }
    root->data = level[levelL];
    //第三步，确定当前根节点的左子树的层序序列 和中序序列，右子树的层序序列 和中序序列
    root->lchild = create(levelL+1,levelR,inL,k-1);
    root->rchild = create(levelL+1,levelR,k+1,inR);
    return root; //总是忘记这个小可爱~~
}

int main() {
    cin>>n;
    for(int i = 0; i < n; ++i)
        cin>>level[i];
    for(int i = 0; i < n; ++i)
        cin>>in[i];
    Node* root = create(0,n-1,0,n-1);
    preorder(root);
    return 0;
}

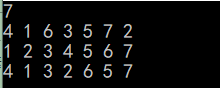
运行结果：

posted @ 2020-02-29 14:04 tangq123 阅读(1120) 评论(0) 收藏举报

刷新页面返回顶部

碎觉(¦3[▓▓]

层序+中序 = 二叉树

公告