广度优先搜索BFS---求出矩阵中“块”的个数
题目：
给出一个 m x n 的矩阵，矩阵中的元素为0或1。如果矩阵中有若干个 1是相邻的，那么称这些1构成了一个“块”。求给定的矩阵中“块”的个数。
0 1 1 1 0 0 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 1 1 1 0
1 1 1 0 1 0 0
1 1 1 1 0 0 0
例如上面的 6 x 7的矩阵中，“块”的个数为4。
输入格式：
第一行给出 m，n（1<=m，n<= 20）分别表示矩阵的行，列。
每一行给出 n个数（0或者1），共m行。
输出格式：
输出矩阵中“块”的个数。
输入样例：
6 7
0 1 1 1 0 0 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 1 1 1 0
1 1 1 0 1 0 0
1 1 1 1 0 0 0
输出样例：
4
直接上代码。。。
1 #include<iostream> 2 #include<queue> 3 #include<unordered_map> 4 using namespace std; 5 6 const int maxn = 100; 7 struct Node { 8 int x,y; 9 } node;//全局的临时变量 10 int matrix[maxn][maxn]; 11 int m,n,CNT = 0; 12 int X[] = {0,0,1,-1};//控制访问的四个方向,新技能 get !!! 13 int Y[] = {1,-1,0,0}; 14 bool inque[maxn][maxn] = {false};//标记元素是否已经入队---这样不会改变矩阵原本的状态，新技能get !!! 15 bool judge(int i,int j) { 16 if(i < 0 || j < 0 || i>= m||j>= n || matrix[i][j] == 0 || inque[i][j] == true) 17 return false; 18 return true; 19 } 20 void BFS(int i, int j) { 21 queue<Node> que; //定义队列 22 node.x = i,node.y = j; 23 que.push(node); //入队 24 inque[i][j] = true; //标记已经入队 25 while(!que.empty()) { //队列非空 26 Node top = que.front(); //取出队首元素 27 que.pop(); //队首元素出队 28 for(int i = 0; i < 4; ++i) { //访问相邻的四个元素 29 int nowI = top.x + X[i]; 30 int nowJ = top.y + Y[i]; 31 if(judge(nowI,nowJ)) { 32 node.x = nowI,node.y = nowJ; 33 que.push(node); //入队 34 inque[nowI][nowJ] = true;//标记已经入队 35 } 36 } 37 } 38 } 39 40 int main() { 41 cin>>m>>n; 42 for(int i = 0; i < m; ++i) { //初始化矩阵 43 for(int j = 0; j < n; ++j) 44 cin>>matrix[i][j]; 45 } 46 for(int i = 0; i < m; ++i) {//暴力DFS，哈哈哈 47 for(int j = 0; j < n; ++j) { 48 if(matrix[i][j] == 1 && inque[i][j] == false) { //元素为1，并且元素未入过队 49 BFS(i,j); 50 CNT++; 51 } 52 } 53 } 54 cout<<CNT;//输出矩阵中”块“ 的个数 55 return 0; 56 }
运行结果：
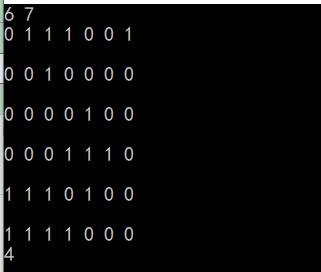
get了两个新技能：
一，设置两个方向数组X,Y来控制4个或者8个方向
二，设置一个全局二维数组，标记元素是否已经入队（而不是访问，因为已经入队的元素，可能还未访问，这是两者的区别），这样可以不改变初始矩阵的状态
总的来说，因为BFS需要队列支持，所以目前我感觉比较难，不过！还好BFS有模版！！！
先要记住大体流程，然后反复练习！！！
