函数4

函数学习4

内容概要

---

• 多层语法糖内部结构
• 有参装饰器
• 递归函数
• 算法之二分法

内容详情

---

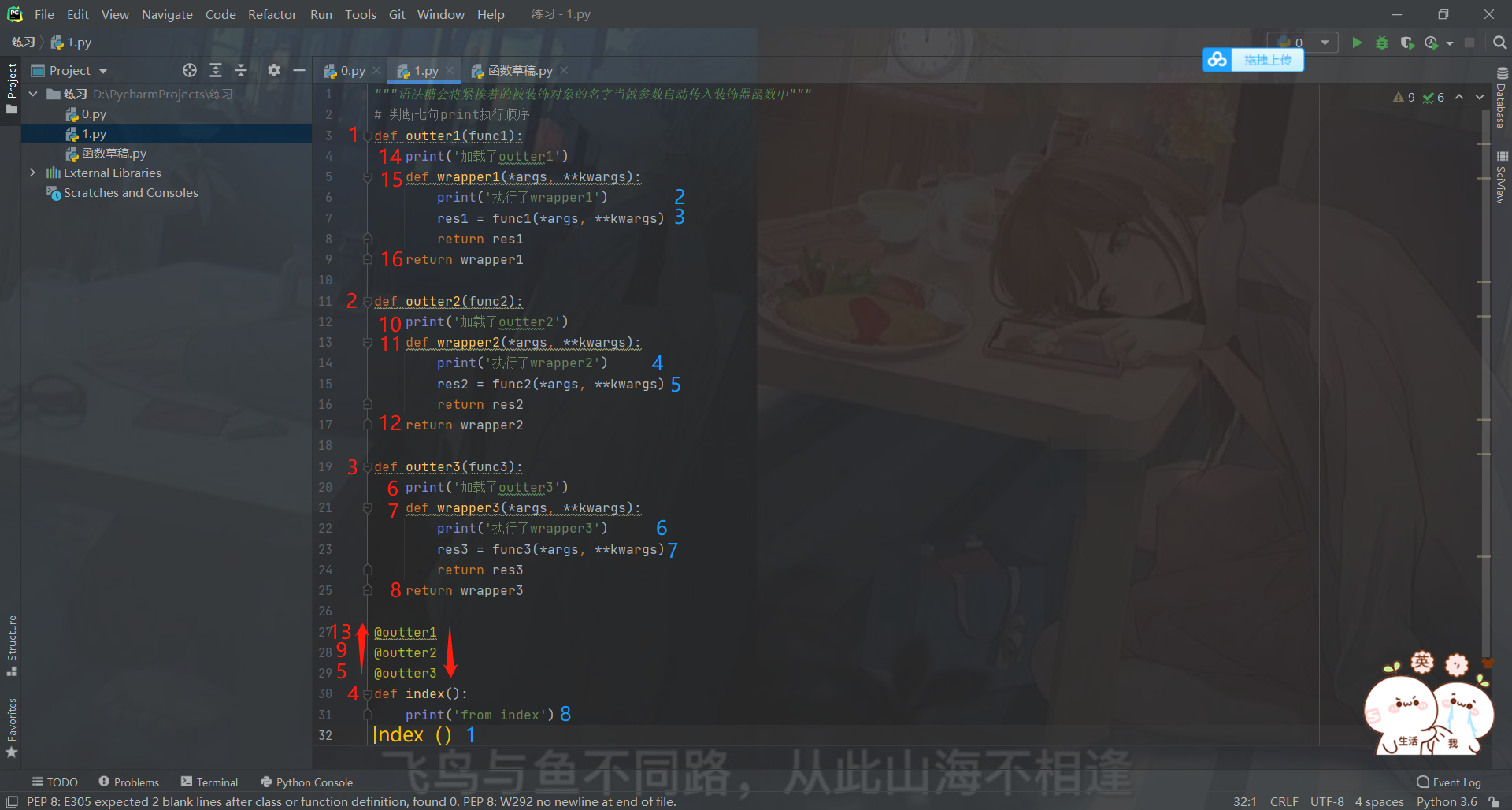
多层装饰器

"""语法糖会将紧挨着的被装饰对象的名字当做参数自动传入装饰器函数中"""
@outter1
@outter2
@outter3
def index():
装饰多个功能由下向上 调用执行由上到下

 

 

有参装饰器

  装饰器外层函数传参只能接收被装饰对象
  装饰器内层函数传参用于被装饰对象传参
  装饰器含参数需要在包一层  记得返回

'''
  函数名加括号 执行优先级最高

  @最外层函数(参数)
    左侧是语法糖结构 右侧是函数名加括号结构   
        先执行函数调用  最外层函数(参数)  返回值是原本装饰器外层函数
        在执行语法糖结构  @内层函数
'''
  有参装饰器目的仅仅是给装饰器传递额外的参数  
  装饰器最多就三层嵌套

递归函数

# 本质:递归函数也称为函数的递归
       函数在运行过程中直接或者间接的调用了自身
# 基本演示
  直接调用自己
  def index():
      print('from index')
      index()
  index()
  间接调用自己
  def index():
      print('from index')
      func()
  def func():
      print('from func')
      index()
  func()
"""
maximum recursion depth exceeded while calling a Python object
最大递归深度超出限制了
python解释器自带的应急机制  在有些编程语言中没有应急机制 代码执行一直到计算机崩溃为止
python最大递归深度 官方给出的是1000 回答997 998 1000都可以
"""
# import sys
  print(sys.getrecursionlimit())  # 获取默认的最大递归深度  1000
  sys.setrecursionlimit(n)  # 还可以修改最大递归深度
  recursion 递归
"""
函数的递归不应该是无限循环的过程 真正的递归函数应该要满足两个要求
    1.每次递归 复杂度必须降低(下一次递归要比上一次递归解答)
        大白话 越往下递归应该离解决问题的答案越近
    2.必须要有明确的结束条件
"""

递归练习

l1 = [1,[2,[3,[4,[5,[6,[7,[8,[9,]]]]]]]]]
'''需求:循环打印出列表中每一个数字'''
def get_num(l):
    for i in l:  # 自带结束条件 并且每次传入的数据都比上一次简单
        if isinstance(i,int):  # 判断某个数据是否属于某个类型
            print(i)
        else:
            get_num(i)
get_num(l1)

算法之二分法

# 算法即解决问题的有效方法
  """
  算法比较偏向于学术研究 很枯燥 并且产出很少
  甚至只有非常大的互联网公司才会有算法部分
  	算法工程师薪资待遇很高 但是产出很少
  	有时候甚至几年都没有任何的成果 有点类似于研究所!!!
  """
二分法：算法里最入门的一个
'''二分法使用有前提: 数据集必须有先后顺序(升序 降序)'''
"""
二分法原理
    获取数据集中间的元素 比对大小
        如果中间的元素大于目标数据  那么保留数据集的左边一半
        如果中间的元素小于目标数据  那么保留数据集的右边一半
    然后针对剩下的数据集再二分
        如果中间的元素大于目标数据  那么保留数据集的左边一半
        如果中间的元素小于目标数据  那么保留数据集的右边一半
    ...
"""
"""
二分法的缺陷
    1.如果要找的元素就在数据集的开头 二分更加复杂
    2.数据集必须有顺序
目前没有最完美的算法 都有相应的限制条件
"""
"""
以后面试的时候  可能会让你手用python写一些算法
    二分法 快排 插入 冒泡 堆排序
"""