回归过程

⭐在任何回归模型求解前先进行方差F检验

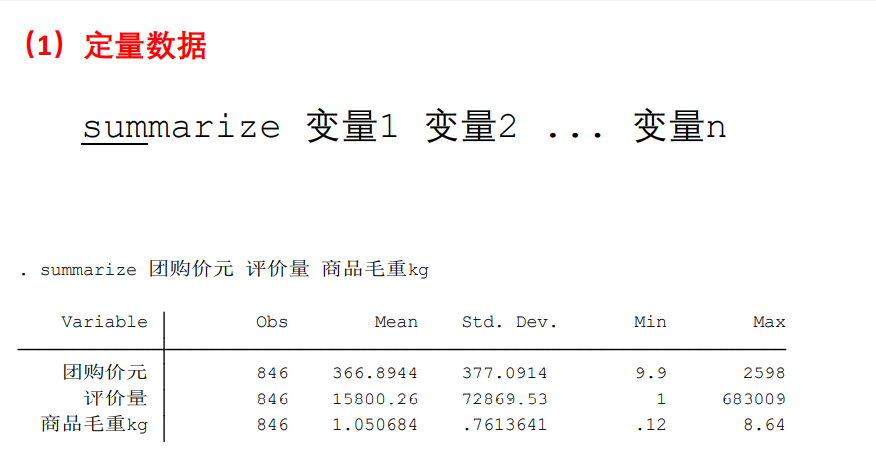
1、描述性统计。列万描述性统计一定要补充说明每个数据的特点

例子如下

 

 

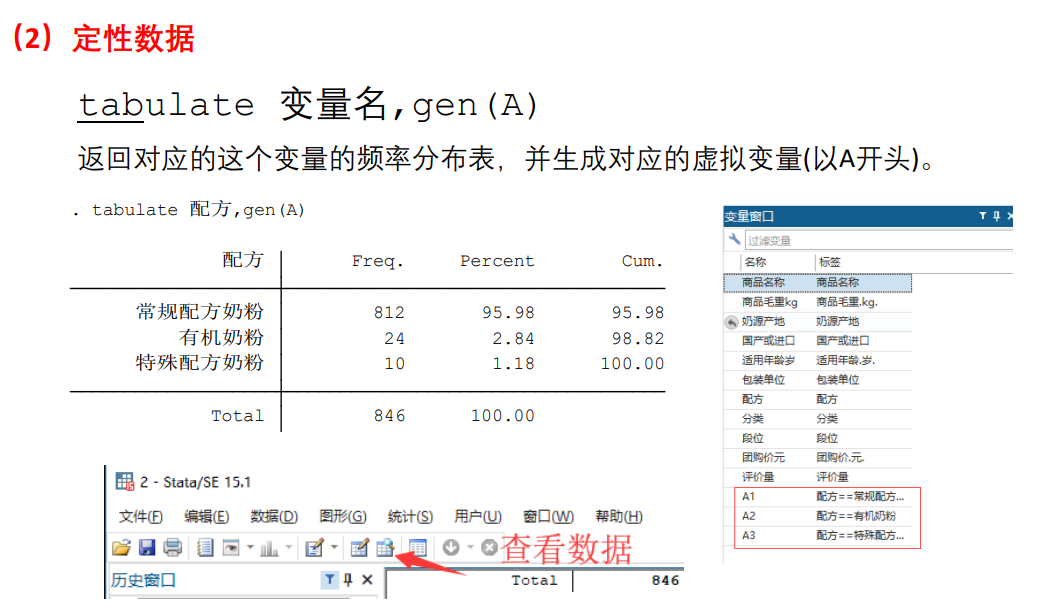
2、线性模型假设

2.1、列出指标总体情况介绍

 

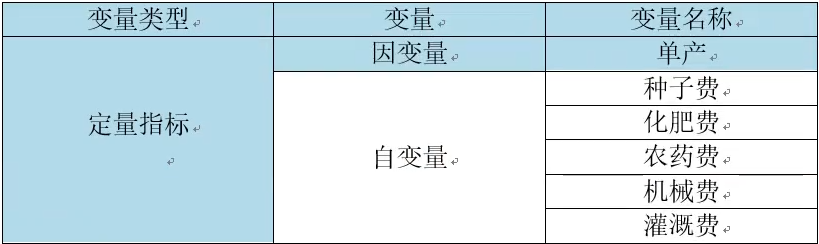
 假设自变量X={x1,x2,x3,x4,x5},因变量y=4,且满足如下线性关系：

 

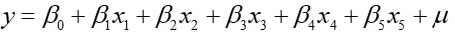
 其中μ为无法观测且完全随机的扰动项。

 

3、模型的求解

一、基于OLS回归分析

1、首先对自变量前的回归系数进行联合显著性检验得到p是否大于0.05，若不大于0.05，则因此在95%的置信区间下，拒绝原假设，认为βi不全为0.

2、列出回归结果：

3、对于所有得到的回归系数βi分布进行显著性t检验，有表中结果课件所有变量xi均不显著，且置信区间全部包含零点。所以该OLS模型显然不能满足我们的要求。鉴此，对数据进行异方差怀特检验及多重共线性VIF检验。

4、异方差怀特检验

第一种方法：绘制残差与拟合值的散点图，观察是否有异方差

 

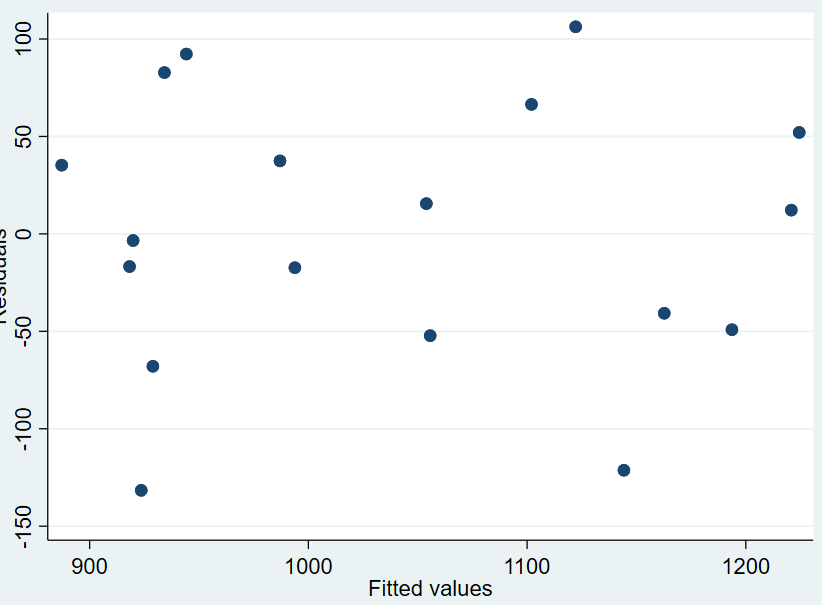
 第二种方法（更为严谨）对OLS模型进行White检验得到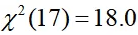，判断p值是否大于0.05，若大于，则我们不能拒绝原假设，可认为不存在异方差

 

 

 5、多种共线性检验

为了检验多重共线性的存在使用方差膨胀因子VIF。

观察VIF是否大于10，若有则认为具有多种共线性。拟对其进行向后逐步回归。

6、标准化向后逐步回归模型求解

原理：

先将所有变量均放入模型，之后尝试将其中一个自变量从模型中剔除，看整个模型解释因变量的变异是否有显著变化，之后将最没有解释力的那个自变量剔除；此过程不断迭代， 直到没有自变量符合剔除的条件。（可以自己先写一个流程图，不要抄）

首先对模型进行方差F检验，得到F（2，15）=20，p=0.0000001<0.05，因此在95%的置信区间下，拒绝原假设，认为βi不全为0

接着列出回归结果

7、模型分析

 判断模型的拟合优度（R2），若模型为解释性模型则可以接受R2不那么大的结果

结论