二叉树初探

二叉树初探

完美二叉树

• 理论基础

  • 完美二叉树，即层数为 \(h\)，而总结点数为 \(2^h - 1\)。

  • 对于每个结点 \(x\) ，左节点为 \(x\times2\)，右节点为 \(x\times2+1\)。

  • 显然可以用递归遍历。

• 存储方式

  • for (int i = 0; i < 1 << n; i++)
    {
    	cin >> tree[i + (1 << n)];
    }
    

• 递归遍历

  • void (int x)
    {
    	if (x >= 1 << n)//即到达叶子节点
            return;
        dfs(x * 2);
        dfs(x * 2 + 1);
    }
    

• 例题

  • P4715 深基16.例1 淘汰赛

二叉树深度

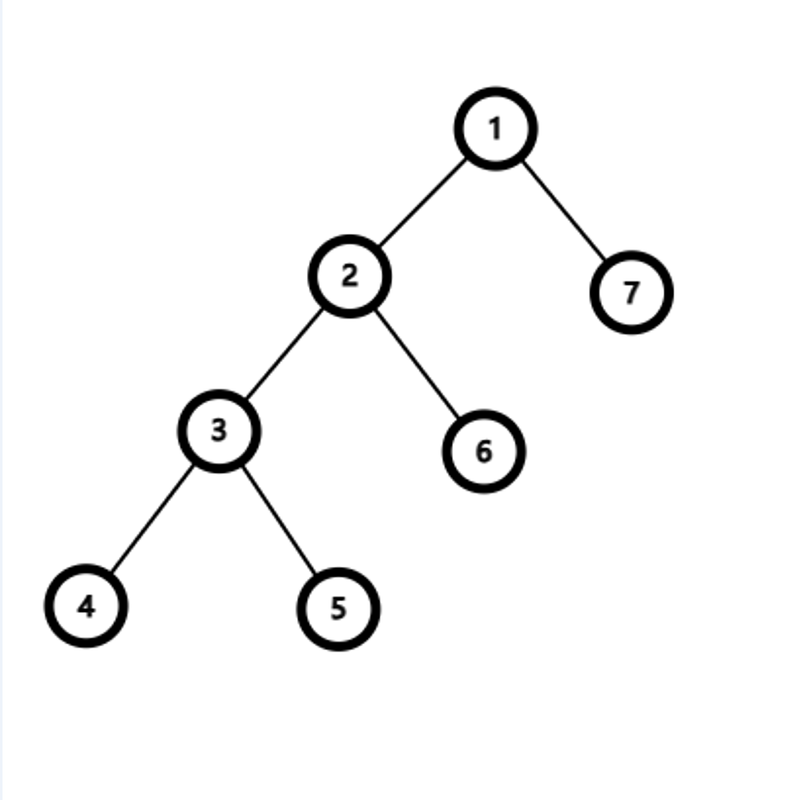
有一个 \(n(n \le 10^6)\) 个结点的二叉树。给出每个结点的两个子结点编号（均不超过 \(n\)），建立一棵二叉树（根节点的编号为 \(1\)），如果是叶子结点，则输入 0 0。

建好这棵二叉树之后，请求出它的深度。二叉树的深度是指从根节点到叶子结点时，最多经过了几层。

输入格式

第一行一个整数 \(n\)，表示结点数。

之后 \(n\) 行，第 \(i\) 行两个整数 \(l\)、\(r\)，分别表示结点 \(i\) 的左右子结点编号。若 \(l=0\) 则表示无左子结点，\(r=0\) 同理。

输出格式

一个整数，表示最大结点深度。

样例 #1

样例输入 #1

7
2 7
3 6
4 5
0 0
0 0
0 0
0 0

样例输出 #1

4

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2e5 + 7;

int l[N], r[N];
int n;

int dfs(int x)
{
	if (!x)
	{
		return 0;
	}
	return max(dfs(l[x]), dfs(r[x])) + 1;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}
	cout << dfs(1);
	return 0;
}

二叉树的遍历

层次遍历

即BFS。

1 2 7 3 6 4 5

深度优先遍历

• 前序遍历

  • 先访问根节点，再遍历左子树，最后遍历右子树。

  • void pre_order(int x)
    {
    	printf("%d ", x);
        if (t[x].left) pre_order(t[x].left);
        if (t[x].right) pre_order(t[x].right);
    }
    

  • 1 2 3 4 5 6 7

• 中序遍历

  • 先遍历左子树，再访问根节点，最后遍历右子树。

  • void pre_order(int x)
    {
        if (t[x].left) pre_order(t[x].left);
        printf("%d ", x);
        if (t[x].right) pre_order(t[x].right);
    }
    

  • 4 3 5 2 6 1 7

• 后续遍历

  • 先遍历左子树，再遍历右子树，最后访问根节点。

  • void pre_order(int x)
    {
        if (t[x].left) pre_order(t[x].left);
        if (t[x].right) pre_order(t[x].right);
        printf("%d ", x);
    }
    

  • 4 5 3 6 2 7 1

• 美国血统

  • 思路

    • 通过前序遍历找到当前二叉树的根（即前序遍历中第一个位置的值）。
    • 然后可以在中序遍历中找出当前二叉树根所在的位置，此时可以得到左子树和右子树的大小，从而递归。

  • 例子

    • 前序遍历
      • 1 2 3 4 5 6 7
    • 中序遍历
      • 4 3 5 2 6 1 7
    • 第一次，在前序遍历中找到 \(1\)，然后在中序遍历中找 \(1\) 的位置，显然 4 3 5 2 6 在以 \(1\) 为根的左子树内，而 7 在以 \(1\) 为根的右子树内，从而提取左右两个区间进行递归。

  • 代码

    • void build(int l1, int r1, int l2, int r2)
      {
      	for (int i = l2; i <= r2; i++)
          {
      		if (a[l1] == b[i])
              {
                  build(l1 + 1, l1 + i - l2, l2, i - 1);
                  build(l1 + i - l2 + 1, r1, i + 1, r2);
                  cout << a[l1];
              }
          }
      }