欧几里得

0. 在openEuler(推荐)或Ubuntu或Windows(不推荐)中完成下面任务，要用git记录实现过程，git commit不能低于5次

1. 严格按照《密码工程》p112伪代码实现ExtendedGCD（int a, int b, int *k, int *u, int *v）算法（10')

2.根据ExtendedGCD 实现计算模逆元的函数int modInverse(int a, int m) ，返回a相对于m的模逆元（3‘）

3. 在测试代码中计算74模167的模逆元。自己再设计至少两个类似测试代码。（2’）

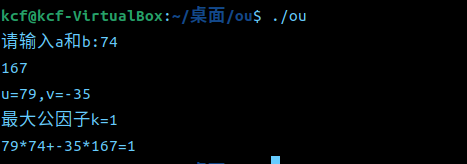
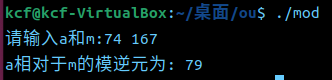
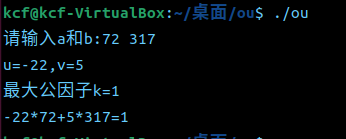
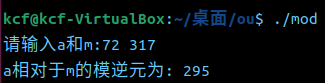
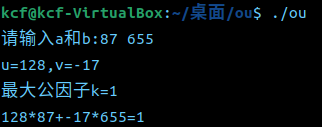
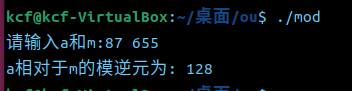
4. 提交代码和运行结果截图，git log截图

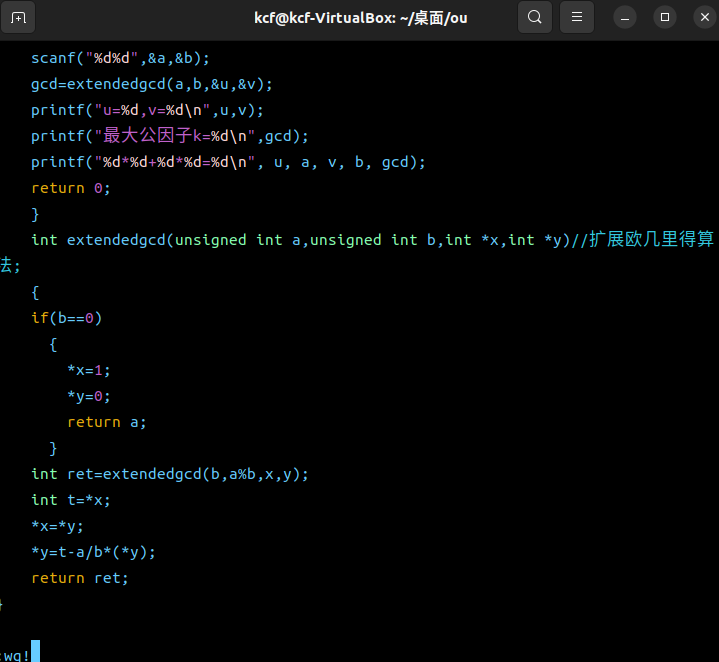
#include<stdio.h>
int main()
{
    unsigned int a,b;
    int u,v,gcd;
    int extendedgcd(unsigned int a,unsigned int b,int *x,int *y);
    printf("请输入a和b:");
    scanf("%d%d",&a,&b);
    gcd=extendedgcd(a,b,&u,&v);
    printf("u=%d,v=%d\n",u,v);
    printf("最大公因子k=%d\n",gcd);
    printf("%d*%d+%d*%d=%d\n", u, a, v, b, gcd);
    return 0;
    }
    int extendedgcd(unsigned int a,unsigned int b,int *x,int *y)//扩展欧几里得算法;
    {
    if(b==0)
      {
        *x=1;
        *y=0;
        return a;
      }
    int ret=extendedgcd(b,a%b,x,y);
    int t=*x;
    *x=*y;
    *y=t-a/b*(*y);
    return ret;
}

#include<stdio.h>  

  

// 扩展欧几里得算法，计算最大公因子以及对应的x和y  

int extendedgcd(unsigned int a, unsigned int m, int *x, int *y) {  
    if (m == 0) {  
        *x = 1;  
        *y = 0;  
        return a;  
    }  
    int x1, y1;  
    int gcd = extendedgcd(m, a % m, &x1, &y1);  
    *x = y1;  
    *y = x1 - (a / m) * y1;  
    return gcd;  
}  
// 计算模逆元  
int modInverse(int a, int m) {  
    int x, y;  
    int gcd = extendedgcd(a, m, &x, &y);  
    // 确保a和m互质  
    if (gcd != 1) {  
        printf("a和m不互质，无法计算模逆元\n");  
        return -1;  
    }  
    // 因为x可能是负数，所以需要调整它到非负范围内  
    x = (x % m + m) % m;  
    return x;  
}  
int main() {  
    unsigned int a, m;  
    printf("请输入a和m:");  
    scanf("%u%u", &a, &m); 
    int inv = modInverse(a, m);  
    if (inv != -1) {  
        printf("a相对于m的模逆元为: %d\n", inv);  
    }  

      

    return 0;  

}

5. 提交使用Markdown并转为pdf格式，或者使用doc、docx格式