通过平抛运动公式推导出第一宇宙速度

通过平抛运动公式推导出第一宇宙速度

本文中需要推导公式的地方使用了python的sympy包进行符号推导
日常生活中，我们向前平行地面扔出一个物体会发生什么？显然，物体会最终落回地面，并且落地时间t和物体初始高度y有如下关系：

\[y = \frac{1}{2}gt^2 \]

那我们扔出物体的初速度v更快呢，显然物体会飞得更远，不过根据上面的公式，物体在经过同样的t秒后还是会落地的，似乎初速度v不会对落地时间有什么影响。
等等，如果地面无限平，无限大，上面的结论看起来是正确的，可问题是，地面不是平的，地面是个球形。

所以在初速度足够大，以至于地面的曲率变得很明显的时候，物体需要下落的距离不再是最开始的y，而是会比y多了一点，因为物体在空中下降了初始高度y的同时，地面相比原先也“下降”了那么一点，这里记为\(y_0\)。
回到标题，如何推导出第一宇宙速度？我们知道，第一宇宙速度也就是物体在距离地球最近的轨道上绕着地球飞而不会坠落到地球上的速度。在忽视空气阻力，地表起伏的情况下，几乎可以将第一宇宙速度看成物体可以贴地飞行而不受地表向上支持力的速度。
第一宇宙速度和平抛运动有什么关系？当物体运动了t秒，重力使物体下降了\(\frac{1}{2}gt^2\)米，与此同时地面也“下降”了\(y_0\)米，如果可以在物体运动了任意时间t的情况下，都使

\[y_0 = \frac{1}{2}gt^2 \]

成立，岂不是说物体相对于它正下方的地面，永远保持在初始高度y的地方，当这个y无线趋近于0的时候，不就相当于物体在贴地飞行吗，物体此时的速度不正是第一宇宙速度吗。
那么根据这个思路，我们要做的就是求出\(y_0\)的大小，怎么求？首先我们以地心为原点建立平面直角坐标系，将地球抽象成一个圆进行分析，为了分析方便，只取第一象限的点进行分析。因为圆相对于x轴，y轴轴对称，所以圆在4个象限内的图像完全一致，我们在第一象限得出的结论可以推广到其余的3个象限。

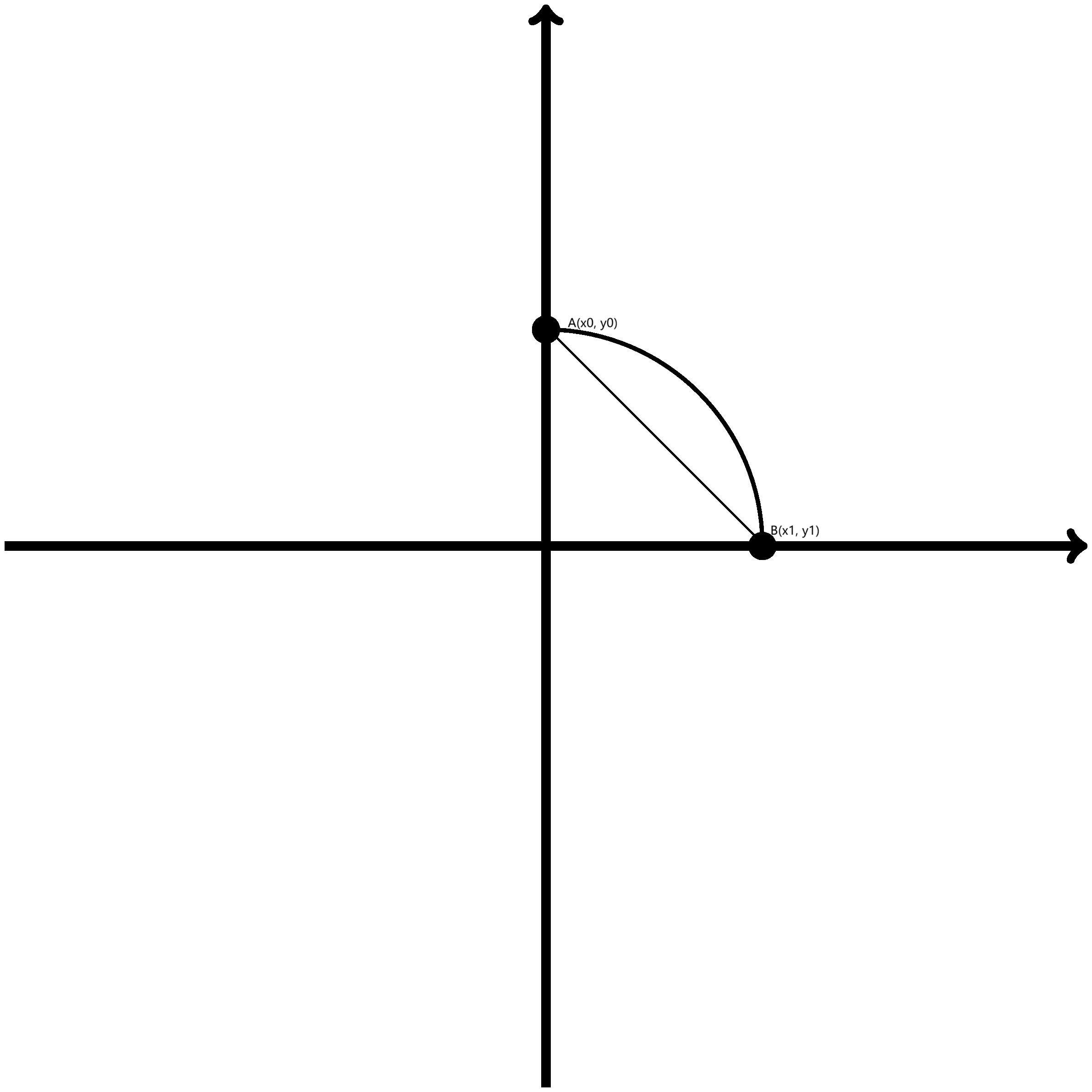
在圆上任取两点A和B，设从A点抛出物体，由于是平抛，所以物体沿着A点切线方向运动，在这里首先求出A点的切线方程。

圆在第一象限的函数可以表示为

\[y = \sqrt{r^2 - x^2} r \geq x \]

因此，A点的切线方程通过求导可得

\[y = -x_0(r^2 - {x_0}^2)^{-\frac{1}{2}}x + {x_0}^2(r^2-{x_0}^2)^{-\frac{1}{2}}+(r^2-{x_0}^2)^\frac{1}{2} \]

如果之后物体没有受到力，它将一直沿着切线运动下去，当运动到B点横坐标x1时，此时对应在切线上的点P的坐标纵应该是

\[{x_0}^2(r^2-{x_0}^2)^{-\frac{1}{2}}+(r^2-{x_0}^2)^\frac{1}{2}-x_0x_1(r^2 - {x_0}^2)^{-\frac{1}{2}} \]

而实际上物体会受到重力作用，从而落到B点
在此，我们做出一次简化，假设物体开始运动的A点在y轴上，这样的话\(x_0\)等于0。因为圆是旋转对称图形，所以在圆上A点的具体位置不影响最终结论。
此时，切线上P点和点B之间纵坐标的差，代表了物体受重力影响下在x轴方向上运动了\(x_1 - x_0\)米时，在y轴方向上运动的距离

\[y_0 = r - \sqrt{r^2 - {x_1}^2} r \geq x_1 \]

令\(y_0=\frac{1}{2}gt^2，x_1=vt\)，则可以得到

\[r - \sqrt{r^2-v^2t^2}-\frac{1}{2}gt^2 = 0 \]

\[v = \frac{\sqrt{gt^2(4r-gt^2)}}{2t} \]

当t无限趋近于0时，\(v = \sqrt{gr}\)
由此，我们从平抛运动推导出了第一宇宙速度的公式。