题目:
给出组合数C(n,m), 表示从n个元素中选出m个元素的方案数。例如C(5,2) = 10, C(4,2) = 6.可是当n,m比较大的时候,C(n,m)很大!于是xiaobo希望你输出 C(n,m) mod p的值!
input:
输入数据第一行是一个正整数T,表示数据组数 (T <= 100) 接下来是T组数据,每组数据有3个正整数 n, m, p (1 <= m <= n <= 10^9, m <= 10^4, m < p < 10^9, p是素数)
output:
对于每组数据,输出一个正整数,表示C(n,m) mod p的结果。
- 原理:
组合数公式:
![]()
lucas的转换:
代码:
# include <iostream>
# include <algorithm>
using namespace std;
typedef long long ll;
ll quickpow(ll a,ll b,ll c)//快速幂
{
ll ans=1;
while(b)
{
if(b&1)
ans=(ans*a)%c;
a=(a*a)%c;
b>>=1;
}
return ans;
}
ll cz(ll a,ll b,ll c)
{ if(b==0) return 1; //eg. c(5,0)=1
int i;
if(b>a-b) b=a-b; //减小运算次数 c(5,3)=c(5,2)
ll up=1,down=1;
for(i=1;i<=b;i++)
{
up=(up*(a-i+1))%c;
down=(down*i)%c;
}
return up*quickpow(down,c-2,c)%c;
}
ll lucas(ll a,ll b,ll c)
{
if(b==0) return 1;
return cz(a%c,b%c,c)*lucas(a/c,b/c,c);//公式的应用
}
int main()
{
ll re;
cin>>re;
int i,j;
for(i=0;i<re;i++)
{
ll a,b,c;
cin>>a>>b>>c;//输入的c只能为质数
cout<<lucas(a,b,c)<<endl;
}
return 0;
}




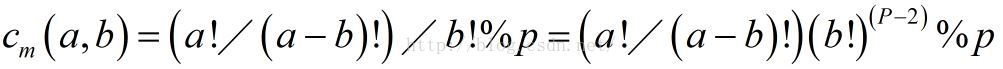

 浙公网安备 33010602011771号
浙公网安备 33010602011771号