书是老师推荐的刘鹏翻译的那本,名字叫《计算机图形学——基于3d图形开发技术》
1.1游戏制作流程
1.GPU,图形处理单元,专注于图形内容的处理器,是交互式图形学的核心内容。 可以分为可编程阶段和硬件阶段。
2.游戏制作流程:建模——动画——渲染
3.常见的游戏建模方案:多边形网格
1.2多边形网格
1.一般为三角形和正方形
2.多边形:应为凸多边形 (后补图),且具有共面性——三角形可视为最简单的多边形。
3.若要提高图形的分辨率,则可以对多边形网格进行进一步的细分操作。
1.2.1多边形网格的表示方式
1.n个三角形网格,有3n个顶点,将其输入到顶点缓冲区,形成三角形列表(相邻的三角形共用一个顶点,所以顶点缓冲区存在冗余)
2.索引三角形列表:将不重复的每个顶点输入缓冲区,并给于对应标号,在索引缓冲区给出组成一个三角形的顶点的3个标号。(后补图)
3.索引缓冲区的格式可定义为16或者32位无符号整数,即可以存2的16/32次方个顶点。
4.各个顶点通过GPU的顶点处理阶段进行独立转换,并存储于后转换缓冲区中,当缓冲区缺失时才需要对顶点实施处理,否则只要从缓冲区中获取
5.平均缓冲缺失率(ACMR):将每个三角形所处理的平均顶点数量称为平均缓冲缺失率。——该指标用于测量渲染的性能
6.最坏情况下ACMR=3,正常情况下ACMR=0.5~1.
7.封闭式网格中,三角形数量为顶点数量的2倍. 所以若后转换存储区够大,顶点无需重复处理,则ACMR=n/2n=0.5
8.ACMR取决于传递至GPU中的三角形的排列顺序,高局部特征(三角形间有尽量多的顶点重合)的处理顺序比低局部特征(三角形几乎没有顶点重合)的处理顺序来的高效。(后补图)
1.2.2 三角带表示方式
1.由一系列的邻接三角形构成,(后补图),相接在一起的三角形在处理的时候,第一个三角形需要处理3个顶点,接下来的每个三角形只需要处理一个顶点
2.若有n个三角形则需处理顶点:3+(n-1)=n+2——ACMR=n+2/n (当n趋近于无穷的时候,ACMR趋近于1)
1.2.3表面法线
1.在进行光照模拟的时候需要利用表面法线。
2.多边形网格的顶点可以视为平滑表面采样后的顶点数据。(近似)——> 法线可以直接赋予顶点,以使顶点发现约为采样点处的平滑表面的法线。
3.公共顶点的三角形需执行均值计算: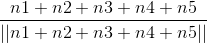
1.3 模型的导入和导出
1.为解决数据输出格式与运行期游戏程序的不匹配问题,可采取插件和脚本机制实现。
2.插件方式:可与主程序实现交互操作,进而提供主程序无法支持的功能集。
3.脚本:通过解释方式加以执行,且由主程序执行。——大多数图形软件包均提供了自身的脚本语言。(速度较慢,却易于编码,采用优化方式访问主程序)
4.图元可分为几何图元(点,线段,多边形,曲线和曲面,可作为独立实体进行渲染)和图像图元【光栅图元】
1.4坐标系统
1.笛卡尔提出的坐标系包含左手法则(LHS)和右手法则(RHS)(后补图)
2.若将基于RHS的工具包生成的多边形网格导入LHS软件包中,则往往需要重新建模(可分为2步)
3.第一步:调整顶点顺序 <p1,p2,p3>——> <p1,p3,p2> 【第一点不动,2和3点互换】
第二步:对象的z坐标和视见参数逆置 (后补图)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号