canny图像处理

 

title: Canny图像分割
date: 2021-11-27 13:40:36
description: Canny图像处理
id: 65010
tags: hexo
categories: 图像处理

基于Canny的图像分割

图像分割方法分类

​ 现有的图像分割方法主要分以下几类：基于阈值的分割方法、基于区域的分割方法、基于边缘的分割方法以及基于特定理论的分割方法等。

<!–more–>

image-20211127130443477

​ 图1(a)是一个理想的边缘所具备的特性。每个灰度级跃变到一个垂直的台阶上。而实际上，在图像采集系统的性能、采样率和获取图像的照明条件等因素的影响，得到的边缘往往是模糊的，边缘被模拟成具有“斜坡面”的剖面，如图1(b)所示，在这个模型中，模糊的边缘变得“宽”了，而清晰的边缘变得“窄”了。

​ 图像的边缘有方向和幅度两种属性。边缘通常可以通过一阶导数或二阶导数检测得到。一阶导数是以最大值作为对应的边缘的位置，而二阶导数则以过零点作为对应边缘的位置

​ 图像边缘是图像最基本的特征，所谓边缘(Edge) 是指图像局部特性的不连续性。灰度或结构等信息的突变处称之为边缘。例如，灰度级的突变、颜色的突变,、纹理结构的突变等。边缘是一个区域的结束，也是另一个区域的开始，利用该特征可以分割图像

canny算法简介

起源

​ Canny边缘检测算子是John F. Canny于 1986 年开发出来的一个多级边缘检测算法。更为重要的是 Canny 创立了边缘检测计算理论（Computational theory of edge detection）解释这项技术如何工作。

通常情况下边缘检测的目的是在保留原有图像属性的情况下，显著减少图像的数据规模。有多种算法可以进行边缘检测，虽然Canny算法年代久远，但可以说它是边缘检测的一种标准算法，而且仍在研究中广泛使用。

准则

​ Canny 的目标是找到一个最优的边缘检测算法，最优边缘检测的含义是：

(1)最优检测：算法能够尽可能多地标识出图像中的实际边缘，漏检真实边缘的概率和误检非边缘的概率都尽可能小；

(2)最优定位准则：检测到的边缘点的位置距离实际边缘点的位置最近，或者是由于噪声影响引起检测出的边缘偏离物体的真实边缘的程度最小；

(3)检测点与边缘点一一对应：算子检测的边缘点与实际边缘点应该是一一对应。

为了满足这些要求 Canny 使用了变分法（calculus of variations），这是一种寻找优化特定功能的函数的方法。最优检测使用四个指数函数项表示，但是它非常近似于高斯函数的一阶导数。

算法流程

Canny边缘检测算法可以分为以下5个步骤：

  1. 应用高斯滤波来平滑图像，目的是去除噪声

  2. 找寻图像的强度梯度（intensity gradients）

  3. 应用非最大抑制（non-maximum suppression）技术来消除边误检（本来不是但检测出来是）

  4. 应用双阈值的方法来决定可能的（潜在的）边界

高斯滤波平滑图片

https://blog.csdn.net/fangyan90617/article/details/100516889

​ 高斯滤波在图像处理概念下，将图像频域处理和时域处理相联系，作为低通滤波器使用，可以将低频能量（比如噪声）滤去，起到图像平滑作用。

​ 高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值用。高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。

image-20211127125413959

image-20211127125128196

找寻图像的强度梯度

梯度 的理解https://blog.csdn.net/qq_36622009/article/details/102900447
https://zhuanlan.zhihu.com/p/113397988#WsZtFtzL

原理介绍

一幅图像可以表示为函数 I = f(x, y)，其中(x, y)为坐标，I表示该像素点的灰度值，梯度gradient表示函数f(x, y)在点(x, y)处最大的变化率，计算的表达式为：

image-20211127125927883

对于图像，我们也可以计算梯度，由于数字图像是有离散的像素点的灰度值构成，所以微分运算就变成了差分，我们可以用相邻两个像素点之间的差分值表示该像素点在某个方向上灰度的变化情况。

​ 可选用的模板：soble算子、Prewitt算子、Roberts模板等等;

一般采用soble算子，OpenCV也是如此，利用soble水平和垂直算子与输入图像卷积计算dx、dy

image-20211127125645860

image-20211127125654044

image-20211127125714539

由此可以得到图像的梯度

image-20211127125738044

为了简化计算，幅值也可以作如下近似：image-20211127125812581

角度为

image-20211127125825243

非最大抑制（non-maximum suppression）技术来消除边误检

数学概念

​ 顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。

近似划分

由于由梯度计算出来的图像边缘是很模糊的，对于存在很多个边缘梯度响应的现象。我们力求在一个梯度方向上找到一个局部的最大值来表示该梯度方向上的梯度响应。在平面360范围内然后把它近似到四个方向，分别代表水平，垂直和两个对角线方向（0°,45°,90°,135°），每个区域的梯度角给一个特定值，代表四个方向之一，如下图所示
image-20211127131334741

优点

这样做的好处是便于计算，便于理解,把在每一个区域内的梯度方向全部近似为一个梯度方向，在这近似的一个梯度方向前后寻求最大值。

缺点

没有插值处理，计算的每一个点的梯度在它的8邻域的梯度方向并不是你所 划分的梯度方向，所处的像素点不是整像素，是小数。

image-20211127131508517

插值处理（2种方法）

现在我们可以在划分好的梯度方向上寻求局部梯度最大值，将当前像素的梯度强度与沿正负梯度方向上的两个像素进行比较。如果当前像素的梯度强度与另外两个像素相比最大，则该像素点保留为边缘点，否则该像素点将被抑制。但是当出现最大值梯度方向不在整像素，而是亚像素，通常为了更加精确的计算，在跨越梯度方向的两个相邻像素之间使用线性插值来得到要比较的像素梯度，如下图蓝线所示情况：
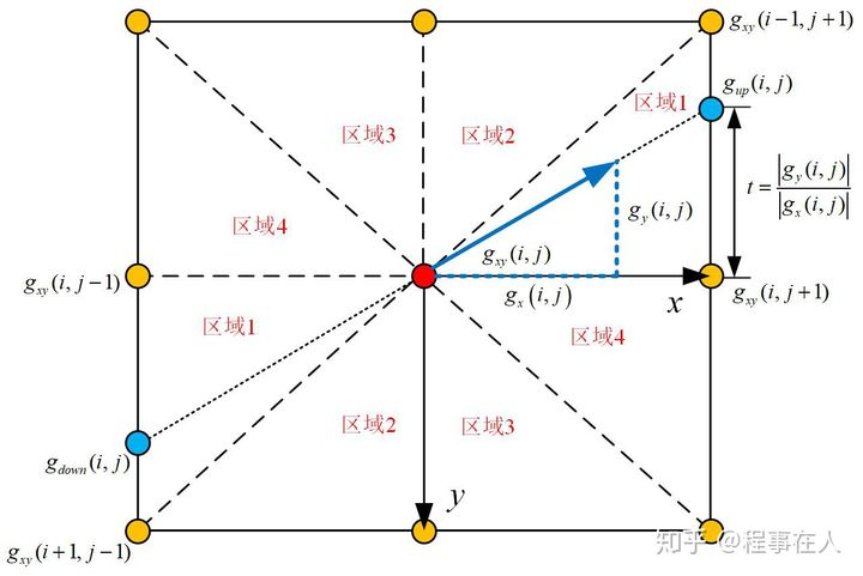
image-20211127124849966

image-20211127131427339

优点
这样做的好处计算更精确，避免了大量的近似估计。
缺点
运算速度慢，计算不太方便，不过插值处理效果比近似划分好多了

双阈值处理边界

具体方法

（1） 根据图像选取合适的高阈值和低阈值，通常高阈值是低阈值的2到3倍
（2） 如果某一像素的梯度值高于高阈值，则保留
（3） 如果某一像素的梯度值低于低阈值，则舍弃
（4） 如果某一像素的梯度值介于高低阈值之间，则从该像素的8邻域的寻找像素梯度值，如果存在像素梯度值高于高阈值，则保留，如果没有，则舍弃

两个阈值是有区别的：

高的那个阈值是将要提取轮廓的物体与背景区分开来，就像阈值分割的参数一样，是决定目标与背景对比度的；

低的阈值是用来平滑边缘的轮廓，有时高的阈值设置太大了，可能边缘轮廓不连续或者不够平滑，通过低阈值来平滑轮廓线，或者使不连续的部分连接起来。两个阈值：T1，T2。大于T1的称为强边界。T1和T2之间的为弱边界。

双阈值好处

如果只有强边界，那么边界可能断断续续。而且会少分割。所以弱边界的作用就是解决上面这个问题。如果强边界点的8连通区域内有弱边界点，那么认为该弱边界点为强边界

源代码实现

matlab 自带代码

Img = imread('cameraman.tif'); % 读取图像
M = size(Img);            % 计算图像大小
if numel(M)>2             %判断图像是否是彩色图像
    gray = rgb2gray(Img); % 图像灰度变换
else
    gray = Img;
end
Cimg = edge(gray,'canny');
figure(1);
subplot(121); imshow(gray,[]); title('原图');
subplot(122); imshow(Cimg,[]); title('Canny边缘检测');

自己实现的代码

https://zhuanlan.zhihu.com/p/99959996

https://www.cnblogs.com/tiandsp/archive/2012/12/13/2817240.html

效果图对比

image-20211127131022095

image-20211127131037701

image-20211127131045758

算法对比

相比Sobel、Prewitt等算子，Canny算法更为优异。Sobel、Prewitt等算子有如下缺点：

没有充分利用边缘的梯度方向。

最后得到的二值图，只是简单地利用单阈值进行处理。

而Canny算法基于这两点做了改进，提出了：

1、 基于边缘梯度方向的非极大值抑制。

2、 双阈值的滞后阈值处理。

最优边缘检测，它包括三个方面

1，好检测：尽可能多的标记处实际边缘（多）

2，好定位：标记出来的边缘应该尽可能多的接近实际边缘（准）

3，小响应：图像中的边缘只能标识一次，并且可能存在的图像噪声不应该标识为边缘

这三个方面，恰恰正是Canny算子的目标！Canny提出了判定边缘检测算子的3个准则：信噪比准则、定位精度准则和单边缘响应准则。

这三个方面的另一种说法

1.低失误率，既要少将真的边缘丢弃，也要少将非边缘判为边缘；

2.高位置精度，检测出的边缘应在真正的边界上；

3.单像素边缘，即对每个边缘有唯一的响应，得到的边界为单像素宽。

4.canny法能够尽可能多地标识出图像中的实际边缘；标识出的边缘要与实际图像中的实际边缘尽可能接近。

缺点 ：

Canny算子比较复杂，既要计算多个方向的梯度，又要记录方向和大小，然后又进行NMS非极大值抑制，大小阈值，很复杂。正是因为Canny算子的目标高，所以他实现起来更为困难，但是相比于索贝尔算子，罗伯茨算子，Canny算子效果更好。他实际上是通过寻找图像梯度的局部最大值实现的。这种算子是一个具有滤波、增强以及检测的多阶段的优化算子。

产生的边缘很细，可能就一个像素那么细，没有强弱之分。计算量大，但是准确。图像中的边缘只能标识一次，并且可能存在的图像噪声不应标识为边缘。

参考文章

原理+步骤：

  1. https://blog.csdn.net/saltriver/article/details/80545571
  2. https://baike.baidu.com/item/Canny算子/8821789?fr=aladdin#2
  3. https://blog.csdn.net/qq_41140138/article/details/105516289?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163792713716780271550581%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=163792713716780271550581&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_positive~default-2-105516289.first_rank_v2_pc_rank_v29&utm_term=canny%E8%BE%B9%E7%BC%98%E6%A3%80%E6%B5%8B%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187 （代码可以运行）
  4. https://blog.csdn.net/fengxianghui01/article/details/89475897?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163792625516780357229320%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=163792625516780357229320&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allfirst_rank_ecpm_v1~rank_v31_ecpm-14-89475897.first_rank_v2_pc_rank_v29&utm_term=canny%E8%BE%B9%E7%BC%98%E6%A3%80%E6%B5%8B%E7%AE%97%E6%B3%95matlab&spm=1018.2226.3001.4187 （代码可以运行）
  5. https://blog.csdn.net/u014485485/article/details/78396493?ops_request_misc=&request_id=&biz_id=102&utm_term=canny边缘检测算法matlab&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-7-78396493.first_rank_v2_pc_rank_v29&spm=1018.2226.3001.4187
    （文章里所含代码及例图是返回强度高于 threshold 的所有边缘的）（简短的步骤原理分析）
  6. https://zhuanlan.zhihu.com/p/99959996 （包含代码）
  7. https://www.jianshu.com/p/6023d0ff7bee
  8. https://www.cnblogs.com/tiandsp/archive/2012/12/13/2817240.html （主要是代码，代码可以实现）
    优缺点：
  9. Canny算子比较复杂，既要计算多个方向的梯度，又要记录方向和大小，然后又进行NMS非极大值抑制，大小阈值，很复杂。 产生的边缘很细，可能就一个像素那么细，没有强弱之分。计算量大，但是准确。
  10. https://blog.csdn.net/zhuwei0710/article/details/69222842 （实验结论部分可以参考一些canny算子的优缺点）
  11. https://blog.csdn.net/weixin_33713503/article/details/93408952
  12. https://blog.csdn.net/Lucky_yw/article/details/80079234
  13. https://blog.csdn.net/jacke121/article/details/95213552
  14. http://www.manongjc.com/article/71482.html
posted @ 2021-11-29 15:46  AGAYT  阅读(579)  评论(0)    收藏  举报