【智能优化算法应用】05蚁群算法应用

作者：康慎吾

• 基本蚁群算法的步骤
  
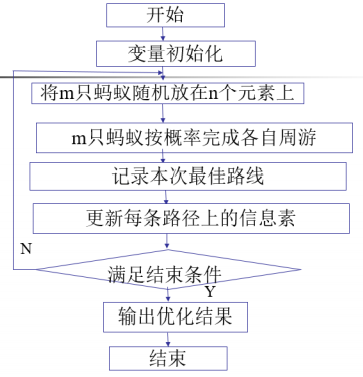
• 信息素的更新有2种：
  （1）挥发（所有路径上的信息素以一定的比率进行减少，模拟自然蚁群的信息素随时间挥发）；
  （2）增强（给评价值“好”(有蚂蚁走过)的边增加信息素）。
• TSP问题
         给定n个城市的集合C={c1,c2,..,cn}及各个城市的位置。TSP问题是找到一条只经过每个城市一次且回到起点的、最短路径的回路。
         初始，将m只蚂蚁随机地放到n座城市，同时，将每只蚂蚁的禁忌表tabu的第一个元素设置为它当前所在的城市。此时各路径上的信息素相等，设 （c为一较小常数），接下来，每只蚂蚁根据路径上残留的信息素和启发式信息（两城市间的距离）独立地选择下一座城市，在时刻t，蚂蚁从城市i转移到城市j的概率为：
  
  
  
• 信息素蒸发系数ρ（0≤ρ≤1）
         ρ反映个体之间相互影响的强弱。1-ρ表示信息素持久性系数。
         ρ过小，以前搜索过的路径被再次选择的可能性过大，会影响到随机性能和全局搜索能力；
         ρ过大，说明路径上的信息素挥发的较多，可以提高随机搜索和全局搜索能力，但过多无用搜索会降低收敛速度。
• 信息素启发式因子α
         信息量对是否选择当前路径的影响程度。值越大，蚂蚁选择以前走过的路径的可能性就越大，搜索的随机性就会减弱；值过小，则易使蚁群的搜索过早陷于局部最优。取值一般为[1,4] 。
• 期望启发因子β
         值越大，蚂蚁在某个局部点上选择局部最短路径的可能性越大，此时算法收敛速度较快，但搜索的随机性减弱，而此时易陷入局部最优解。取值一般为[3，5]。
• 基本蚁群算法的特点
    优点：
         （1)采用正反馈机制，使得搜索过程不断收敛，最终逼近最优解。
         （2）有较强的鲁棒性。对初始路线的要求不高，而且在搜索过程中
  不需要进行人工的调整。此外，参数较少，设置简单。
         （3）搜索过程采用分布式计算方式，多个个体同时进行并行计算，
  大大提高了算法的计算能力和运行效率。
         （4）启发式的概率搜索方式不容易陷入局部最优，易于寻找到全局最优解。
    缺点：
         开始，信息素的作用不明显。初始各路径上的信息素分配差异不明显，要经过很长时间，较好路径上的信息素优势才会凸显，从而最终收敛于较好的路径。
• 蚁群算法解决TSP问题
  （1）初始化随机放置蚂蚁，为每只蚂蚁建立禁忌表 tabu k，将初始节点置入禁忌表中;
  （2）迭代过程

iter=1
while iter=<MAXGEN do ( 执行迭代 )
  for i = 1 to m do ( 对 m 只蚂蚁循环 )
    for j = 1 to n - 1 do ( 对 n 个城市循环 )
      根据式 (1) ，采用轮盘赌方法在窗口外选择下一个城市 j;
      将 j 置入禁忌表 , 蚂蚁转移到 j;
    end for
  end for
  计算每只蚂蚁的路径长度,并找到最短路径 ;
  更新所有路径上的信息素 ;
  iter = iter+ 1;
end while

（3）输出结果, 结束算法。

• 算法应用：TSP问题
  给定n个城市的集合C={c1,c2,..,cn}及各个城市的位置。TSP问题是找到一条只经过每个城市一次且回到起点的、最短路径的回路。

下一节：【智能优化算法应用】06模拟退火算法应用...