10二叉树
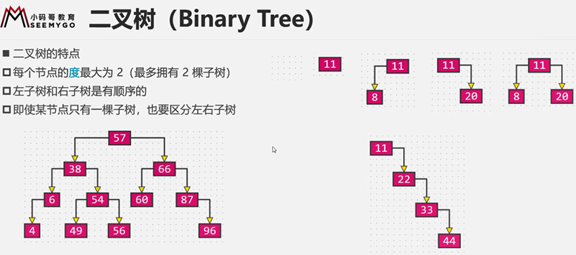
概念
二叉树的性质:
性质1:
性质2:
性质3:
真二叉树
满二叉树
概念
完全二叉树
概念
性质
真题加深
代码是否为完全二叉树
代码
二叉树的遍历
递归-前序遍历
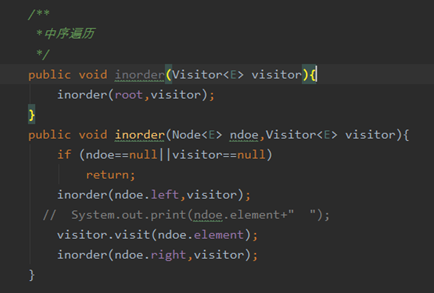
递归-中序遍历
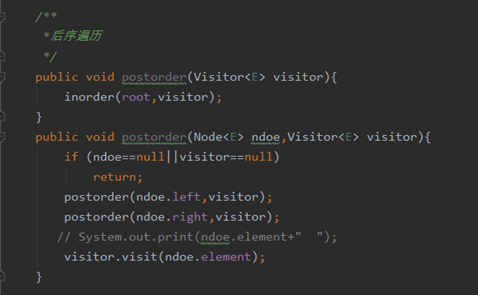
递归-后序遍历
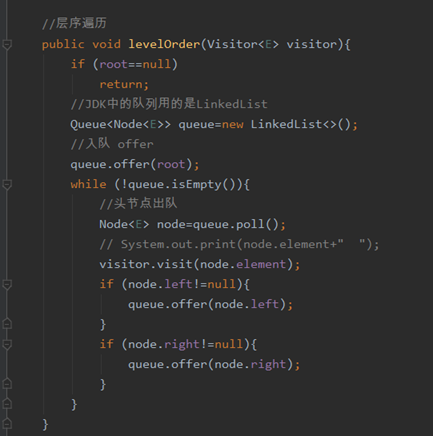
层序遍历
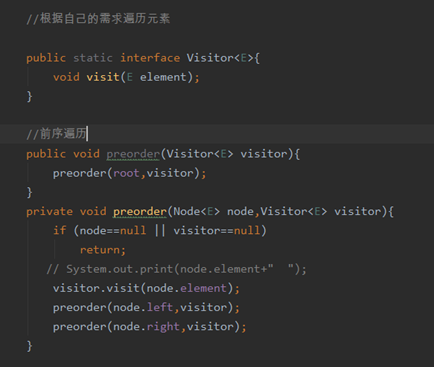
设计一个遍历接口
增强遍历接口
遍历的应用
概述
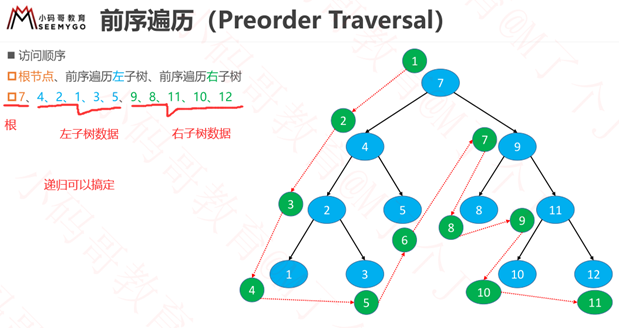
前序遍历
打印树状结构展示
二叉树的高度
递归搞定
非递归—迭代—层序遍历
根据遍历结果重构二叉树
前序+中序
中序+后序
前序+后序:结果可能不唯一
前,中,后 图片参考
前驱节点
概述
上代码
后继节点
概述
上代码
二叉搜索树
概述
比较器
遍历器
二叉搜索树节点
属性和常见方法
查看某个元素是否存在contains()
增加方法add()
删除remove()
概述思路
代码
遍历
最终代码
代码重构:
二叉树作业
二叉树应用练习
翻转二叉树
-------------------------------------------------------------------------------------------------------------------------------
概念
由于二叉树:添加元素没有一个确定的规则,如添加一个元素,但是不知道放在他父节点左边还是右边。只有当把添加规则确定了添加才有意义。如果非要写:可以自己根据需要定义一个规则。
所以一颗普通二叉树的添加没有意义。

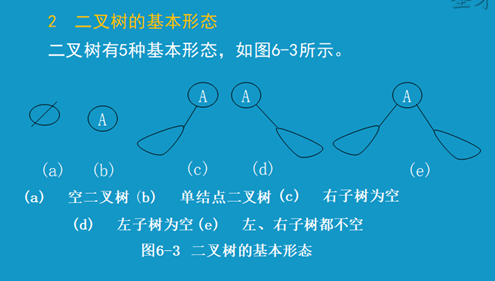
二叉树的性质:
性质1


性质2:
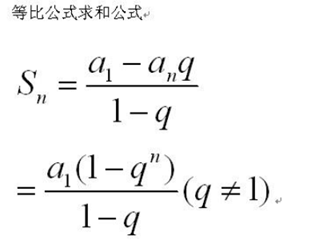

性质3:
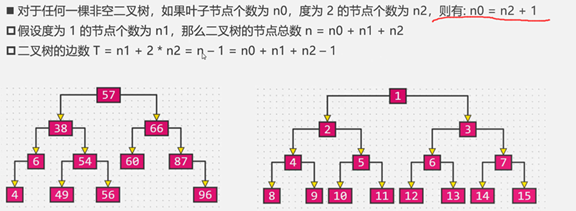
解释一下最后一个
n1+2*n2------节点下的边
n-1--节点上的边(除了根节点上没有线其他都有线)
又n=n0+n1+n2
真二叉树
概念

满二叉树
概念

或者





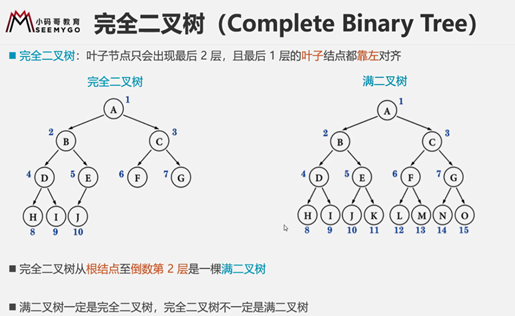
完全二叉树
概念
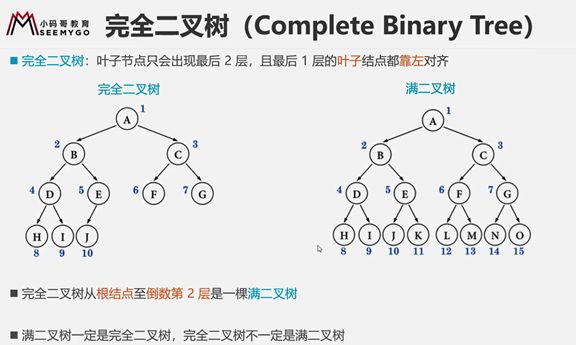
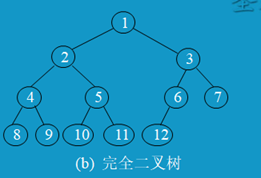
完全二叉树可以理解为:从上到下 从左到右排布




性质


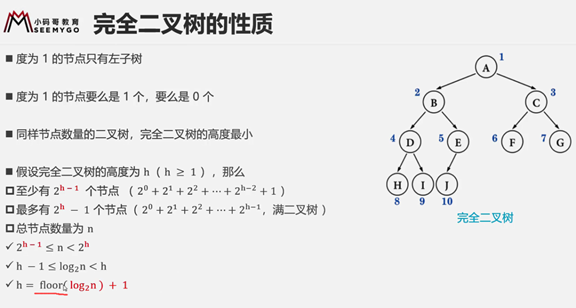
为啥向下取整:因为h肯定是整数。
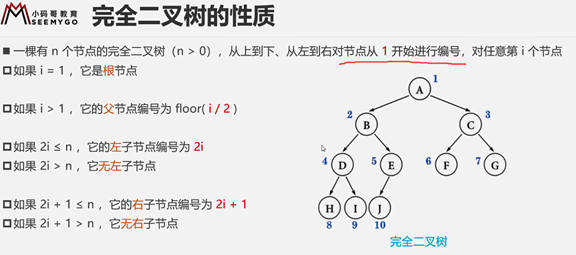

真题加深


把上面两种情况统一

代码是否为完全二叉树
概述
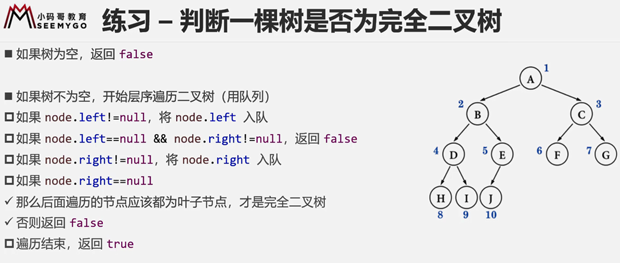
代码
/**
* 层序遍历应用:
*判断一颗树是否为完全二叉树
*/
public boolean isComplete(){
if (root==null) return false;
boolean leaf=false;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()) {
Node<E> node= queue.poll();
//从第一个叶子节点开始 后面都是叶子节点
if (leaf && !isLeaf(node))
return false;
if (node.left!=null)
queue.offer(node.left);
else if(node.right!=null){
//node.left==null && node.right!=null
return false;
}
if (node.right!=null)
queue.offer(node.right);
else {
//node.left==null && node.right==null
//node.left!=null && node.right==null
leaf=true;
}
}
return true;
}
public boolean isLeaf(Node<E> node){
return node.left==null && node.right==null;
}
二叉树的遍历

递归-前序遍历

自己调试一下前序遍历,完全符合这个结论
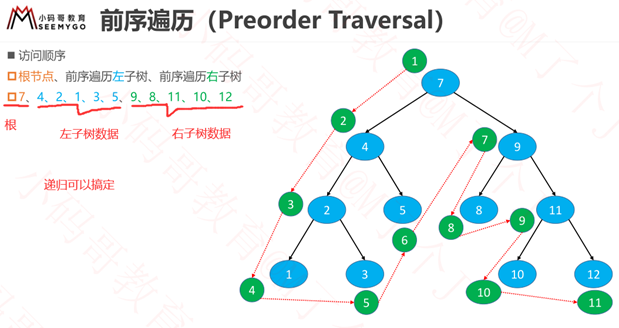
/**
*前序遍历
*/
public void preorderTraversal(){
preorderTraversal(root);//传参根节点
}
private void preorderTraversal(Node<E> node){
if (node==null)
return;
System.out.print(node.element+" ");
preorderTraversal(node.left);
preorderTraversal(node.right);
}
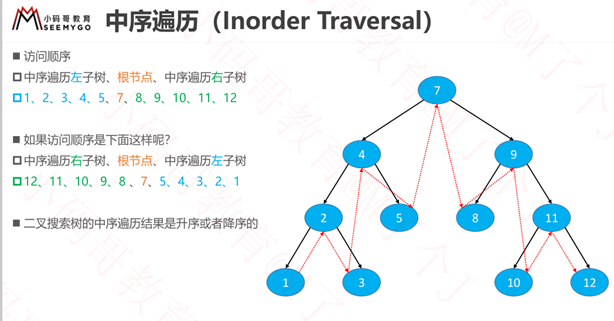
递归-中序遍历
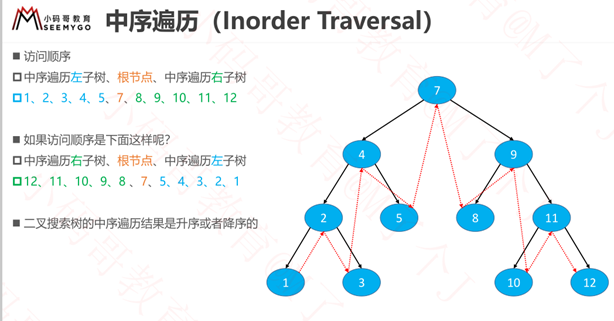
中序遍历根节点是放在中间的,至于先左子树还是先右子树都行。
所以:二叉搜索树的中序遍历结果是升序或者降序的。
/**
*中序遍历
*/
public void inorderTraversal(){
inorderTraversal(root);
}
public void inorderTraversal(Node<E> ndoe){
if (ndoe==null)
return;
inorderTraversal(ndoe.left);
System.out.print(ndoe.element+" ");
inorderTraversal(ndoe.right);
}
inorderTraversal(ndoe.left);
inorderTraversal(ndoe.right);
他们的位置可以互换
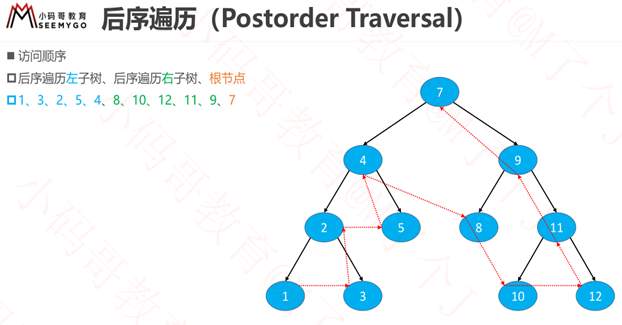
递归-后序遍历
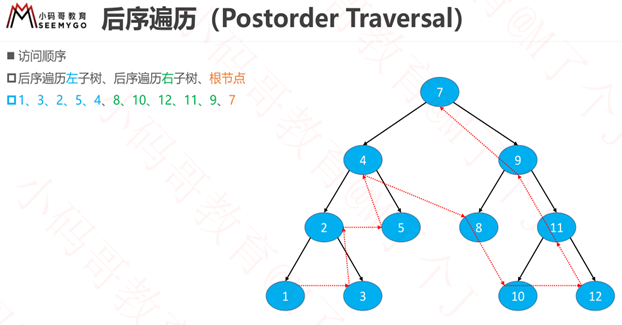
后序遍历-根节点放在最后,遍历左子树,遍历右子树顺序都可以交换的。
/**
*后序遍历
*/
public void postorderTraversal(){
postorderTraversal(root);
}
public void postorderTraversal(Node<E> ndoe){
if (ndoe==null)
return;
postorderTraversal(ndoe.left);
postorderTraversal(ndoe.right);
System.out.print(ndoe.element+" ");
}
层序遍历
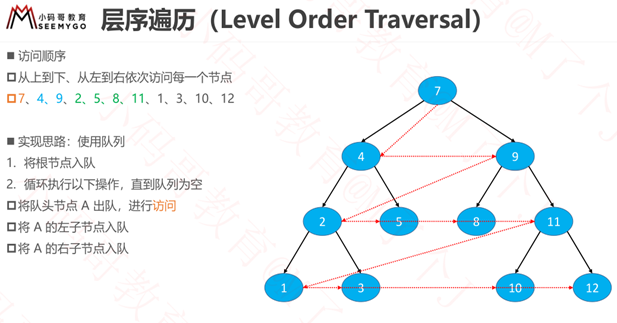
/**
*层序遍历
*/
public void levelOrderTraverlsal(){
if (root==null)
return;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
System.out.print(node.element+" ");
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
}
}
设计一个遍历接口

之前写的遍历逻辑是写死的,直接输出,
但是我现在遍历它,想要对遍历对应的元素做一些操作咋办了?
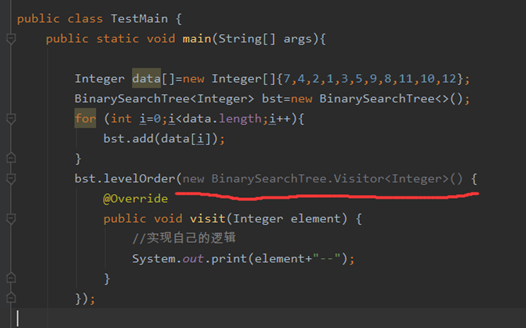

增强遍历接口
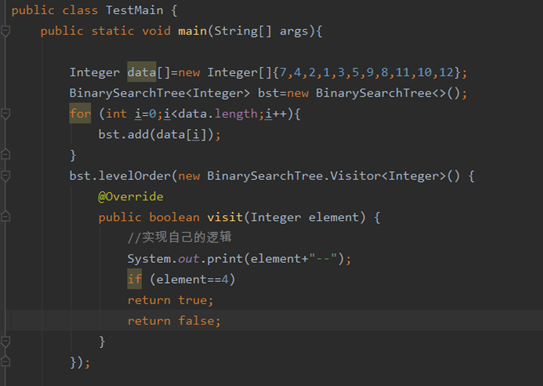
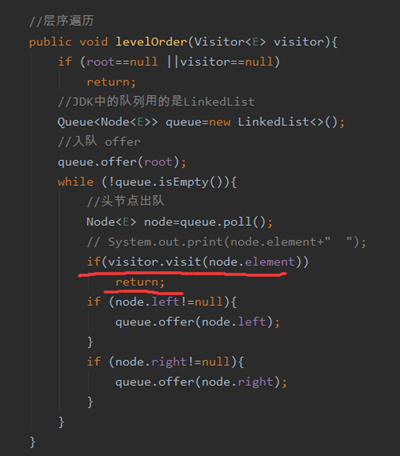
之前的遍历是需要把所有的都遍历完才能退出,但是现在我有一个需求,就是遍历到某个元素(count也可以),就退出遍历。
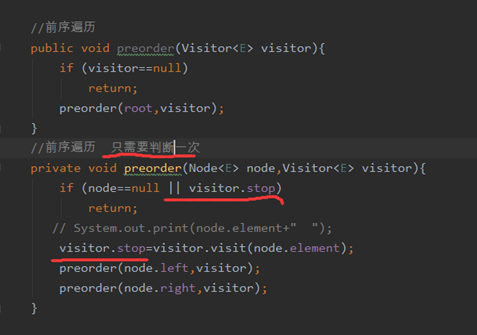
平常函数中停止遍历—直接return
而递归函数中停止遍历—可以在递归终止添加加上出递归条件 如果出递归条件在第一行 那么后面的自然就不会执行了。
一开始进来肯定是false
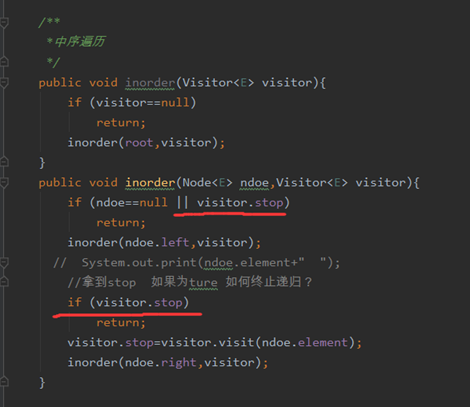
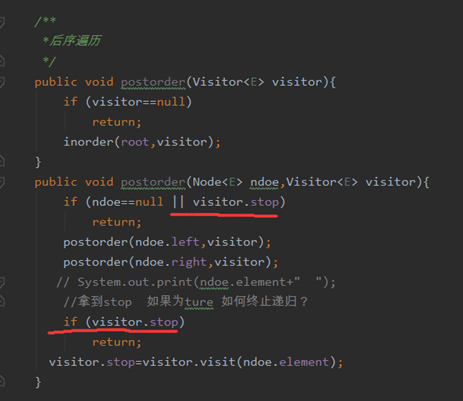
假设右子树返回值拿到一个true,那么visitor不应该调用,
所以还得加上一个判断。不让它打印。
所以第一个判断是终止递归,第二个判断是不让它打印。业务决定代码。


遍历的应用
概述

前序遍历
打印树状结构展示
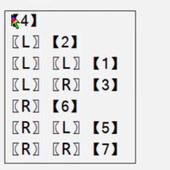
前奏--后面改进
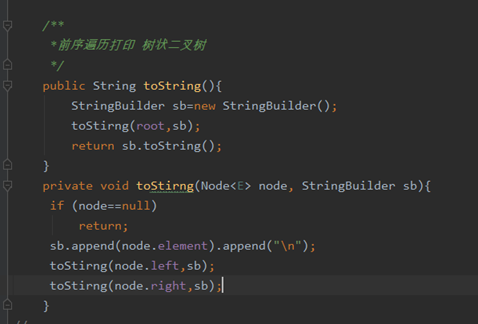
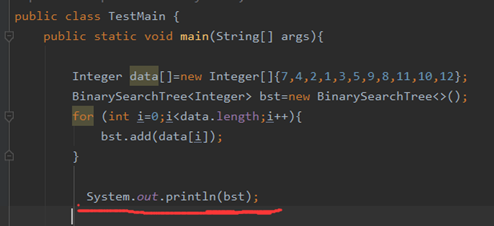
看不出层级关系---继续改进代码

/**
*前序遍历打印 树状二叉树
*/
public String toString(){
StringBuilder sb=new StringBuilder();
toStirng(root,sb,"");
return sb.toString();
}
private void toStirng(Node<E> node, StringBuilder sb,String prefix){
if (node==null)
return;
sb.append(prefix).append(node.element).append("\n");
toStirng(node.left,sb,prefix+"L---");
toStirng(node.right,sb,prefix+"R---");
}
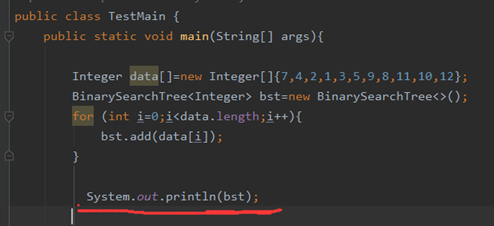
以前的print打印的效果
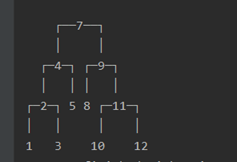
二叉树的高度
递归搞定
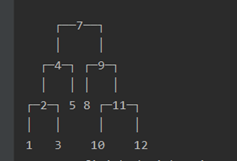
树的高度—根的高度
根节点高度---和它左右子节点有关:
往下类推--符合递归规律---OK

非递归—迭代—层序遍历
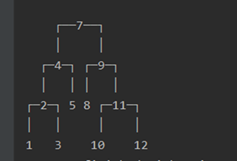
/**
*层序遍历求树的高度
*思路:
* 1:每访问完一层就执行++操作
* 2:关键点是 如何确定 这一层 访问完了
* 首先得确定 你这一层有多少个 有个规律
*
*每当一层中最后一个元素出队--那么队列长度就是下一层元素个数
* 当 levelSize为0时,意味着这一层访问完了 队列长度就是下一层元素个数
*/
public int height(){
if (root==null)
return 0;
int height=0;
//存储每一层元素数量
int levelSize=1;//根节点 默认一个
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
levelSize--;
//入队
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
//当 levelSize为0时,意味着这一层访问完了 队列长度就是下一层元素个数
if (levelSize==0){
levelSize=queue.size();
height++;
}
}
return height;
}
根据遍历结果重构二叉树
根据遍历结构重构二叉树:
对二叉树进行遍历(前,中,后),现在给我遍历的结果,能否利用遍历结果,推导出二叉树长什么样子。

前序+中序
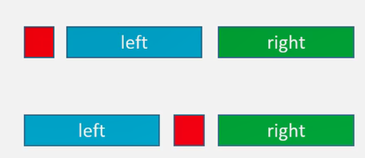
1:由前序遍历可知:第一个为根节点
2:结合中序遍历可知:哪些是左子树,哪些是右子树
3:再回到前序遍历:可知那些是左子树,那些是右子树了。那左子树的第一个必定是左子树的根节点,同理右子树的第一个为右子树的第一个根节点。
补全左子树
4:中序遍历第一个一定是左子树顺着线下面最后一个节点(它可能还含有右子树),结合前序遍历规律,直接就一条线写到,最后一个节点,然后结合中序遍历(节点挨着的分成左子树和右子树。
有些节点可能没有左子树与右子树但是结合输出顺序如果没有直接就弹到线的上一层,很好想,easy)把总的左子树补全完。
记住:
中序遍历:左右子树输出规则:符合 左节点右 但可能出现没有左右子树的情况。
前序遍历左子树先是左一条线输出 而右子树:符合节点左右 但可能出现没有左右节点的情况。
补全右子树
5:中序遍历最后一个一定是右子树一条线下去的最后一个节点(可能含有左子树)。
这个时候就需要一步一步写了。根据结论和前序中序规程看是否合理。
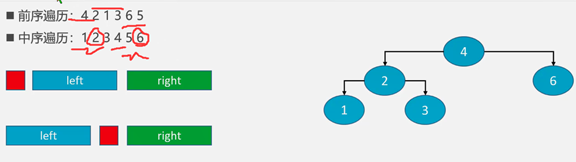


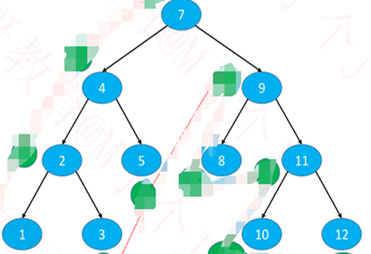
中序+后序
1:由后序遍历可知:最后一个为根节点。
2:结合中序遍历可知:哪些是左子树,哪些是右子树。
中序遍历结论:
中序遍历第一个一定是左子树顺着线下面最后一个节点(它可能还含有右子树).
中序遍历:左右子树输出规则:符合 左节点右 但可能出现没有左右子树的情况。
中序遍历最后一个一定是右子树一条线下去的最后一个节点(可能含有左子树)。
后序遍历结论:
最后一个为根节点,倒数第二个一定是根节点的右子树
后序遍历:左子树最后一个节点一点是根节点的左子树
后序遍历:左右子树输出规则:符合左右节点但可能出现没有左右子树的情况。
3:根据中序+后序规则和给出的各自序列可以写出。


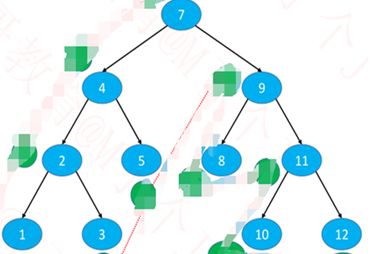
前序+后序:结果可能不唯一

如果左或者右子树中一个是空的情况,根本就不清楚,是左子树还是右子树。
他们只能找到根节点是谁。
如果是一颗真二叉树:那么结果是唯一的。
真二叉树:度为0或者2:
所以:上面的情况:要么左/右子树都为空,要么左/右子树都存在
如果根节点的左右子树都不为空。
前序遍历左子树第一个一定和后序遍历左子树最后一个相同。
那么就可以将整个左右子树的范围区分开来。
那么就可以根据他们各自的规则写出来。


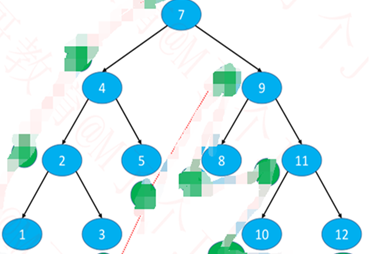
前,中,后 图片参考
前驱节点
概述
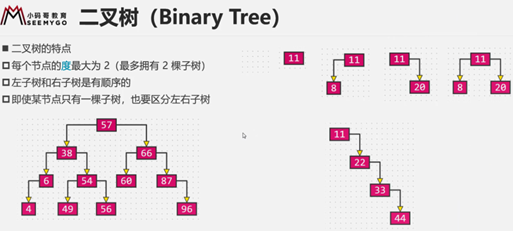
只要是一颗二叉树:就有前驱节点的概念。
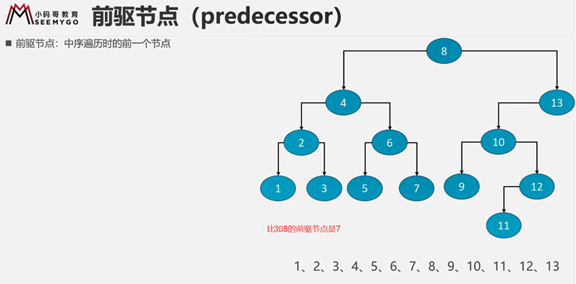
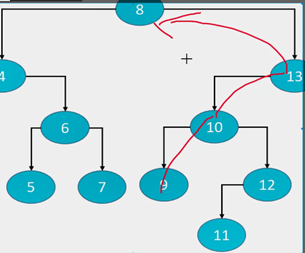
现在给出一颗任意二叉树:求出给定节点的前驱节点。
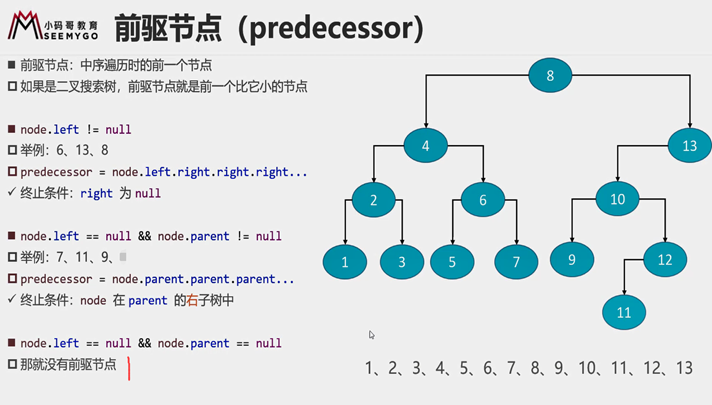
介绍一下第一个和第二个:
第一个:
这个规律任何一颗二叉树都符合:
二叉搜索树就肯定一下就能理解嘛(任何一个节点比它左子树的值都大,任何一个值都比它右子树小那么如果是二叉搜索树,那么该节点的前驱节点一定符合这个规律)
如果是二叉树,中序遍历,那么一定是把左子树最右边的那个遍历完,才会去遍历根节点。(中序遍历左 中 右)
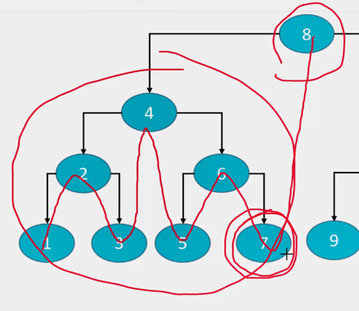
第二个:
二叉搜索树符合这个规律:
往上找的parent如果是左子树:说明比它大,如果是右子树那么比它小,那么就找到该节点的前驱了。
二叉树同样符合这个规律:遍历规律(左 中 后),递归有点难想,记住/理解一下(遍历完8(中节点),那么下一个遍历右子树,那么拆分开又先遍历它左边的,拆分开,这个又是中序遍历,那么又要遍历左边,递归,一定是到底了,然后出递归。所以一拐,一定是前驱。)
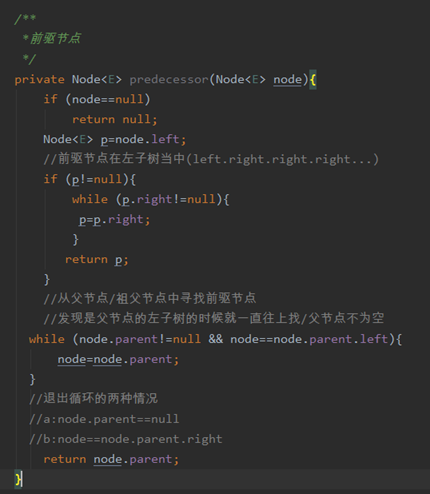
上代码
现在给出一颗任意二叉树:求出给定节点的前驱节点。
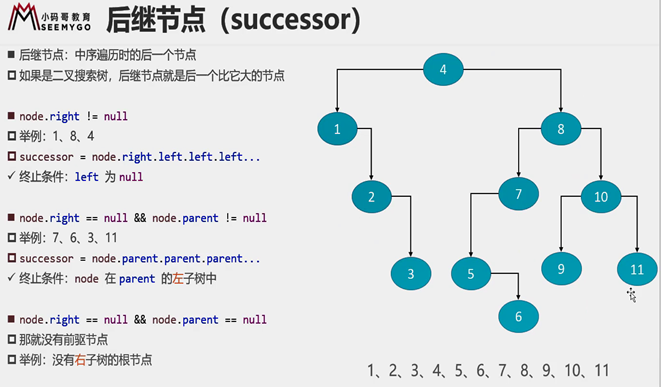
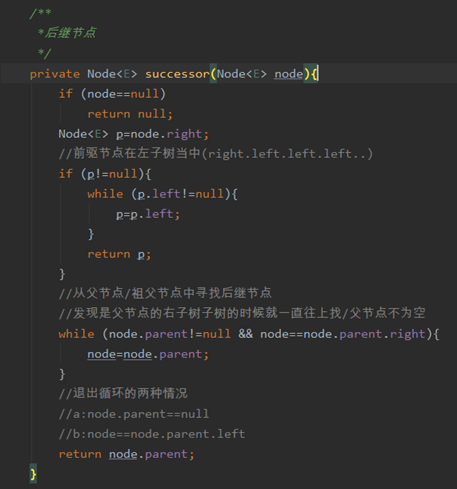
后继节点
概述
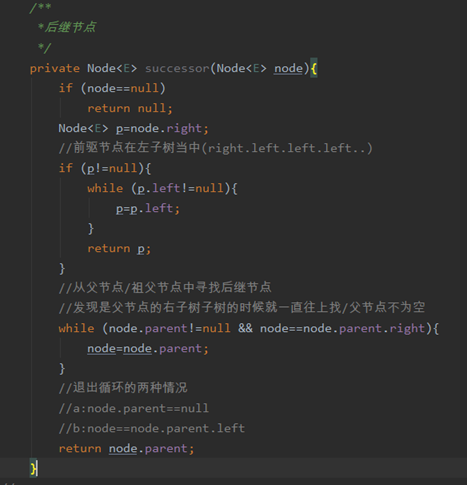
上代码
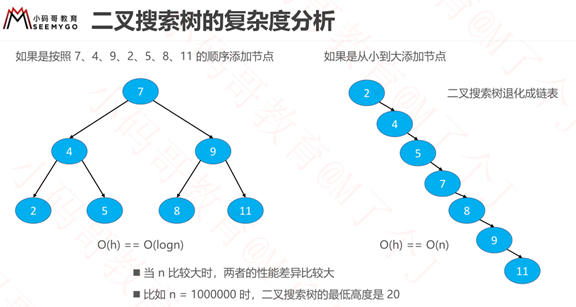
二叉搜索树
概述
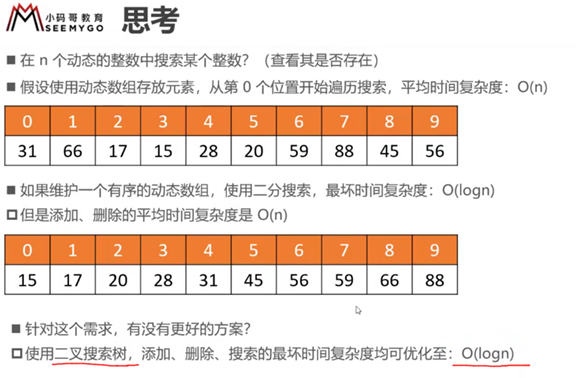
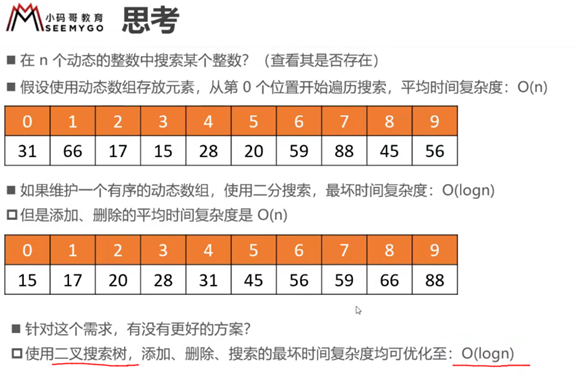
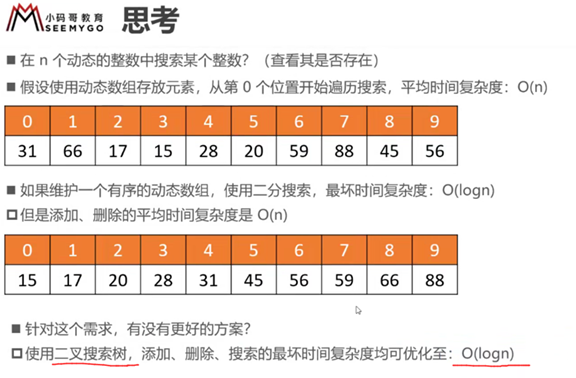



比较器
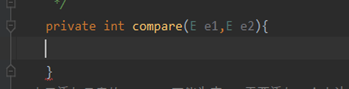
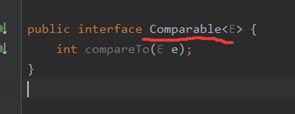
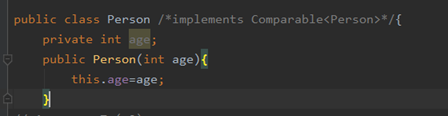
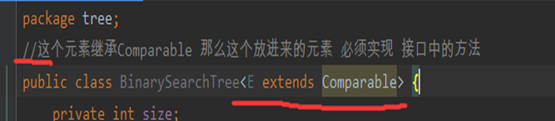
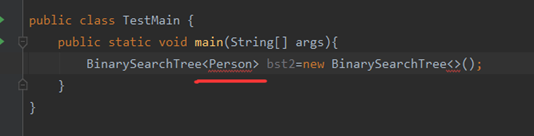
说明需要讲传入元素类型Person中实现接口中的方法
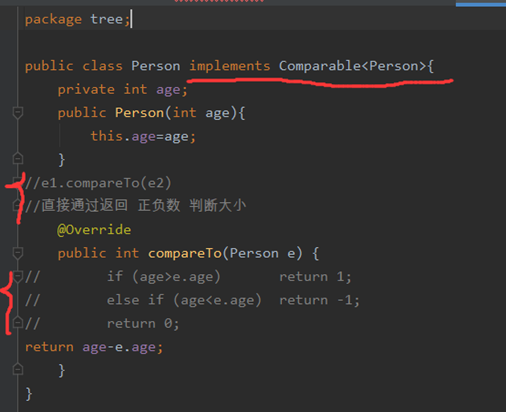
那么现在就可以传入Person了,因为已经实现了接口中的比较方法
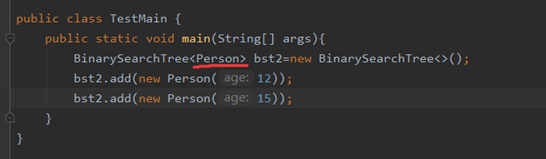
上面设计其实有问题。
按照上面的比较—那么这两棵二叉树的比较规则是一样的。
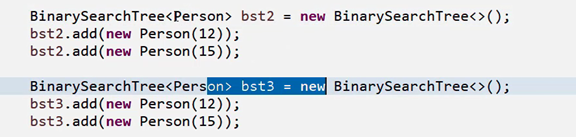
但现在我希望年龄小的节点作为大节点---就是本该存储到左节点但改变比较规则我把它存储到右节点了。
现在的存储数据就和之前的反了—只需要改变一下比较规则而已。看你咋认为他是大是小。
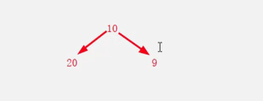
遍历器
验证自己的二叉搜索树是否正确,和它网上的对比一下就OK
http://520it.com/binarytrees/
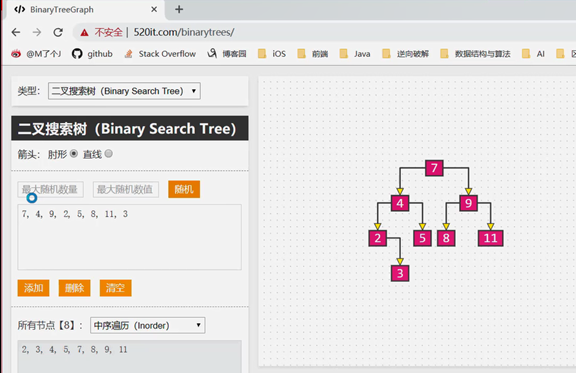

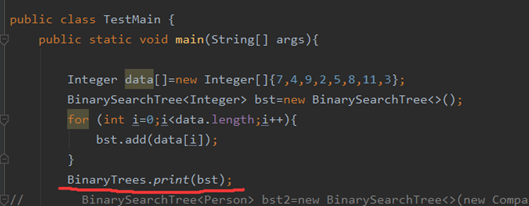
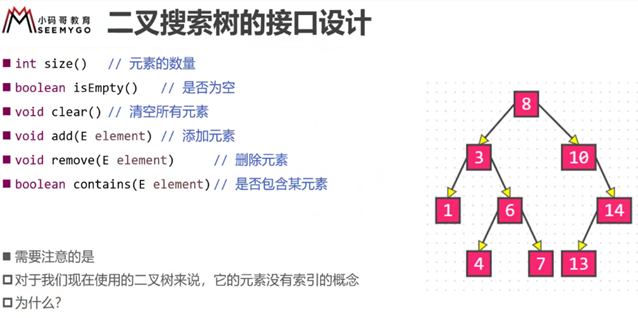
二叉搜索树节点
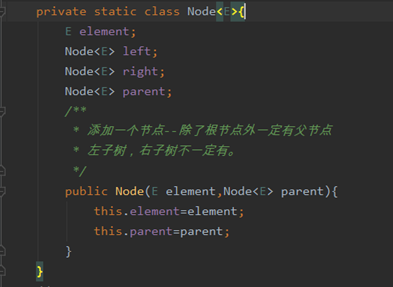
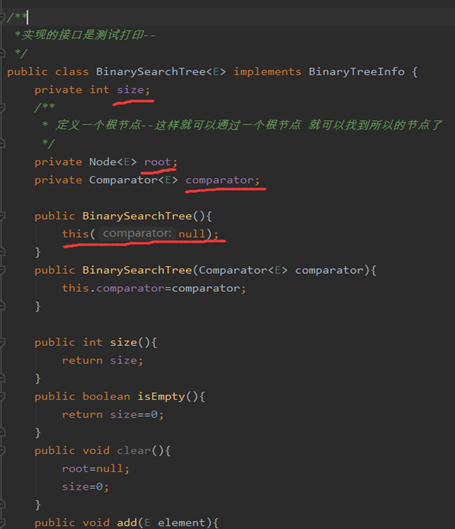
属性和常见方法
查看某个元素是否存在contains()
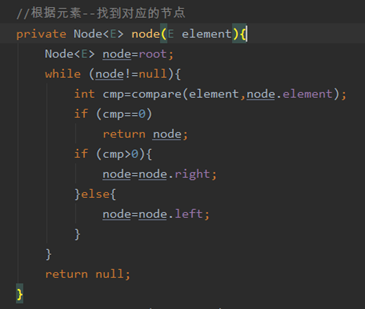
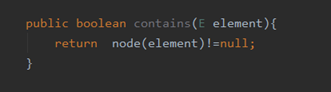
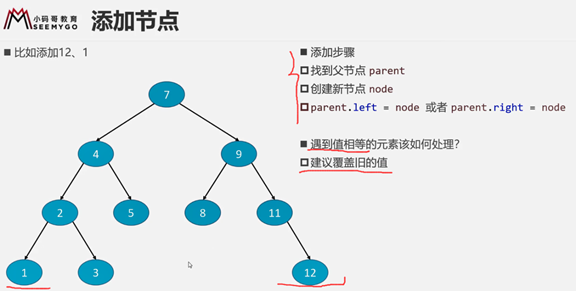
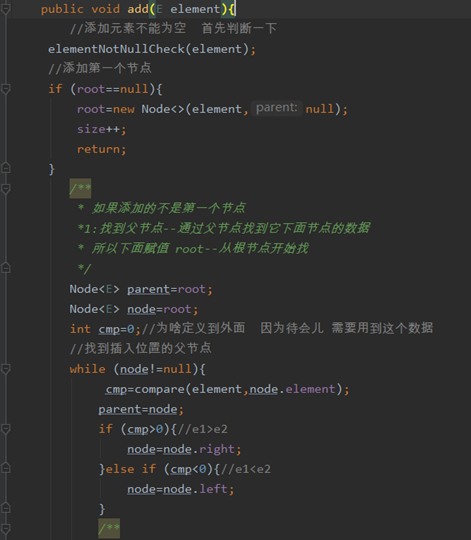
增加方法add()

比如添加 12 1
首先拿数据--和节点比较--
比节点小(和左子树比较)
比节点大(和右节点比较)
依次类推--直到某个合适位置为空(此时退出循环)--添加插入。
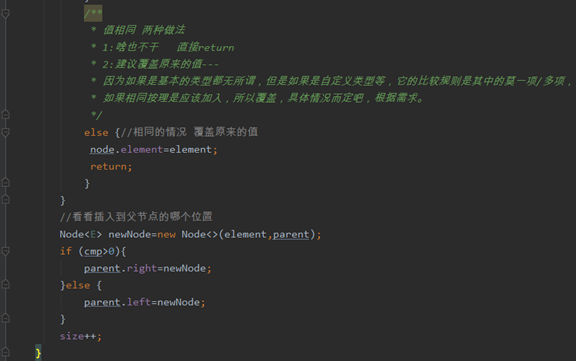
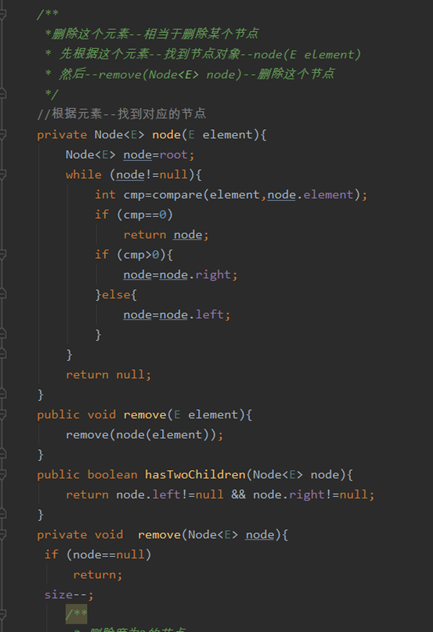
删除remove()
概述思路
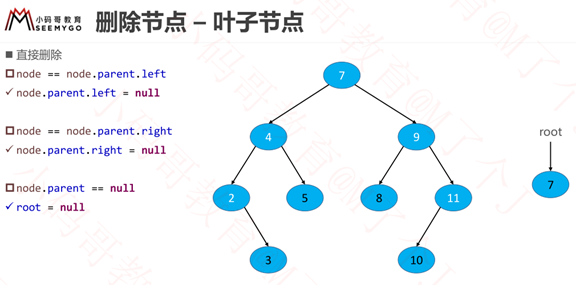
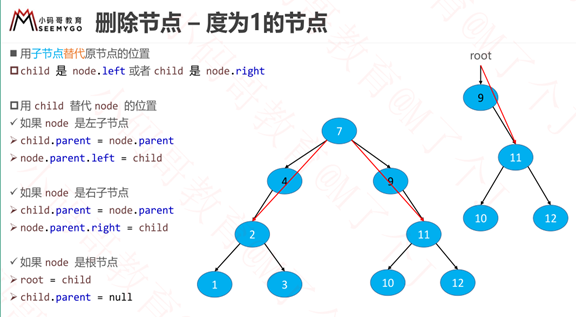
二叉搜索树:要求,
节点中的左子树中任何一个节点都要比它小,
节点中的右子树中任何一个节点都要比它大。
所以找谁取代:
如果是从左子树中就找它的前驱
如果是从右子树中就找它的后继
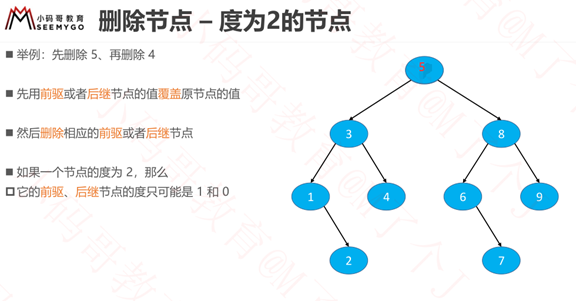
比如删除5后 (这里采用的是用前驱覆盖,当然用后继覆盖一样的)
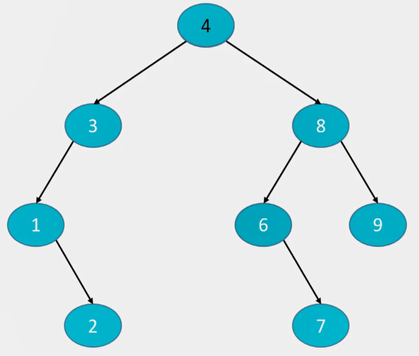
再删除4:
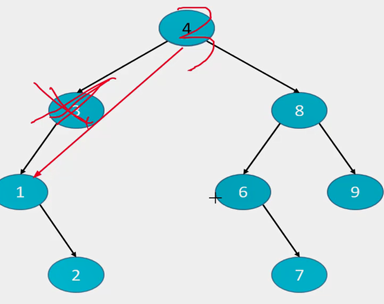
代码
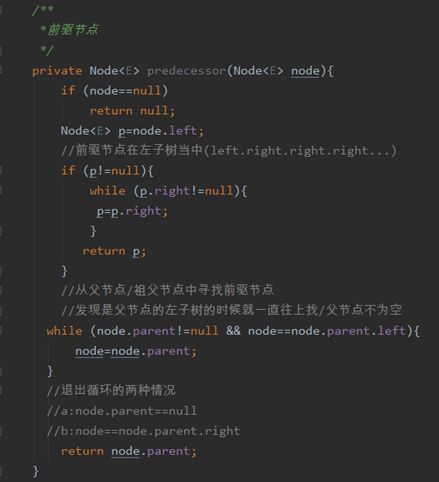

遍历
见二叉树的遍历
最终代码
没用的代码在文件中:比如打印代码。
package tree;
import tree.printer.BinaryTreeInfo;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.Queue;
/**
*实现的接口是测试打印--
*/
public class BinarySearchTree<E> implements BinaryTreeInfo {
private int size;
/**
* 定义一个根节点--这样就可以通过一个根节点 就可以找到所以的节点了
*/
private Node<E> root;
private Comparator<E> comparator;
public BinarySearchTree(){
this(null);
}
public BinarySearchTree(Comparator<E> comparator){
this.comparator=comparator;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size==0;
}
public void clear(){
root=null;
size=0;
}
public void add(E element){
//添加元素不能为空 首先判断一下
elementNotNullCheck(element);
//添加第一个节点
if (root==null){
root=new Node<>(element,null);
size++;
return;
}
/**
* 如果添加的不是第一个节点
*1:找到父节点--通过父节点找到它下面节点的数据
* 所以下面赋值 root--从根节点开始找
*/
Node<E> parent=root;
Node<E> node=root;
int cmp=0;//为啥定义到外面 因为待会儿 需要用到这个数据
//找到插入位置的父节点
while (node!=null){
cmp=compare(element,node.element);
parent=node;
if (cmp>0){//e1>e2
node=node.right;
}else if (cmp<0){//e1<e2
node=node.left;
}
/**
* 值相同 两种做法
* 1:啥也不干 直接return
* 2:建议覆盖原来的值---
* 因为如果是基本的类型都无所谓,但是如果是自定义类型等,它的比较规则是其中的莫一项/多项,
* 如果相同按理是应该加入,所以覆盖,具体情况而定吧,根据需求。
*/
else {//相同的情况 覆盖原来的值
node.element=element;
return;
}
}
//看看插入到父节点的哪个位置
Node<E> newNode=new Node<>(element,parent);
if (cmp>0){
parent.right=newNode;
}else {
parent.left=newNode;
}
size++;
}
/**
*删除这个元素--相当于删除某个节点
* 先根据这个元素--找到节点对象--node(E element)
* 然后--remove(Node<E> node)--删除这个节点
*/
//根据元素--找到对应的节点
private Node<E> node(E element){
Node<E> node=root;
while (node!=null){
int cmp=compare(element,node.element);
if (cmp==0)
return node;
if (cmp>0){
node=node.right;
}else{
node=node.left;
}
}
return null;
}
public void remove(E element){
remove(node(element));
}
public boolean hasTwoChildren(Node<E> node){
return node.left!=null && node.right!=null;
}
private void remove(Node<E> node){
if (node==null)
return;
size--;
/**
* 删除度为2的节点
* a:找到该节点的 前驱/后继节点
* b:用 前驱/后继节点的值 覆盖度为2节点的值
* c:删除后继/前驱节点
*/
if (hasTwoChildren(node)){
//找到后继节点(找前驱节点也可以)
Node<E> s=successor(node);
//用后继节点的值覆盖度为二的值
node.element=s.element;
//删除后继节点
//将度为2的节点指向后继节点,那么就只需要删除后继节点就可以了。
node=s;
}
//删除node节点(注意此时已经指向了s):s它的度必为0或1
//如果是度为1需要找到它的子节点
Node<E> replacement=node.left!=null?node.left:node.right;
if (replacement!=null){//node是度为1的节点
//更改parent
replacement.parent=node.parent;
//更改parent的left,right的指向
if (node.parent==null){//node是度为1的节点并且是根节点
root=replacement;
//这里不需要这一步 replacement.parent=null
//因为更改parent那一步已经完成了这一步。
}
else if (node==node.parent.left){
node.parent.left=replacement;
}else if (node==node.parent.right){
node.parent.right=replacement;
}
}else if(node.parent==null) {//node是叶子节点并且是根节点
root=null;
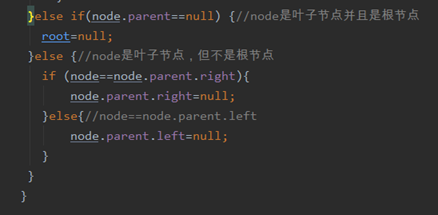
}else {//node是叶子节点,但不是根节点
if (node==node.parent.right){
node.parent.right=null;
}else{//node==node.parent.left
node.parent.left=null;
}
}
}
public boolean contains(E element){
return node(element)!=null;
}
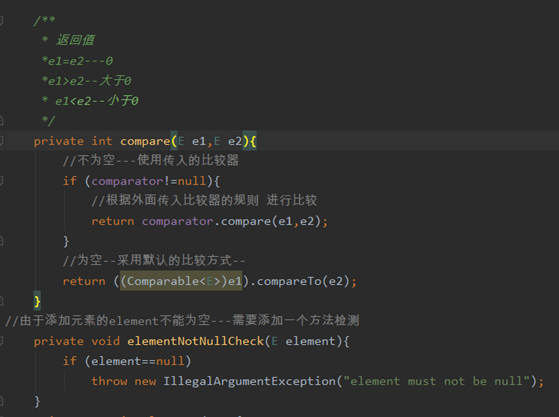
/**
* 返回值
*e1=e2---0
*e1>e2--大于0
* e1<e2--小于0
*/
private int compare(E e1,E e2){
//不为空---使用传入的比较器
if (comparator!=null){
//根据外面传入比较器的规则 进行比较
return comparator.compare(e1,e2);
}
//为空--采用默认的比较方式--
return ((Comparable<E>)e1).compareTo(e2);
}
//由于添加元素的element不能为空---需要添加一个方法检测
private void elementNotNullCheck(E element){
if (element==null)
throw new IllegalArgumentException("element must not be null");
}
private static class Node<E>{
E element;
Node<E> left;
Node<E> right;
Node<E> parent;
/**
* 添加一个节点--除了根节点外一定有父节点
* 左子树,右子树不一定有。
*/
public Node(E element,Node<E> parent){
this.element=element;
this.parent=parent;
}
}
//-------------------------------------------------------------------------------------------------------------------
/**
*前序遍历
*/
public void preorderTraversal(){
preorderTraversal(root);
}
private void preorderTraversal(Node<E> node){
if (node==null)
return;
System.out.print(node.element+" ");
preorderTraversal(node.left);
preorderTraversal(node.right);
}
/**
*中序遍历
*/
public void inorderTraversal(){
inorderTraversal(root);
}
public void inorderTraversal(Node<E> ndoe){
if (ndoe==null)
return;
inorderTraversal(ndoe.left);
System.out.print(ndoe.element+" ");
inorderTraversal(ndoe.right);
}
/**
*后序遍历
*/
public void postorderTraversal(){
postorderTraversal(root);
}
public void postorderTraversal(Node<E> ndoe){
if (ndoe==null)
return;
postorderTraversal(ndoe.left);
postorderTraversal(ndoe.right);
System.out.print(ndoe.element+" ");
}
/**
*层序遍历
*/
public void levelOrderTraverlsal(){
if (root==null)
return;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
System.out.print(node.element+" ");
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
}
}
//---------------------------------------
//根据自己的需求遍历元素
public static abstract class Visitor<E>{
/**
* 接口变为抽象类 是为了存储 stop
* 每一次调用都是唯一的 每次创建对象是唯一的
*/
boolean stop;
/**
*如果返回true 就代表停止遍历
* 如果返回 false 继续遍历
*/
abstract boolean visit(E element);
}
//前序遍历
public void preorder(Visitor<E> visitor){
if (visitor==null)
return;
preorder(root,visitor);
}
//前序遍历 只需要判断一次
private void preorder(Node<E> node,Visitor<E> visitor){
if (node==null || visitor.stop)
return;
// System.out.print(node.element+" ");
visitor.stop=visitor.visit(node.element);
preorder(node.left,visitor);
preorder(node.right,visitor);
}
/**
*中序遍历
*/
public void inorder(Visitor<E> visitor){
if (visitor==null)
return;
inorder(root,visitor);
}
public void inorder(Node<E> ndoe,Visitor<E> visitor){
if (ndoe==null || visitor.stop)
return;
inorder(ndoe.left,visitor);
// System.out.print(ndoe.element+" ");
//拿到stop 如果为ture 如何终止递归?
if (visitor.stop)
return;
visitor.stop=visitor.visit(ndoe.element);
inorder(ndoe.right,visitor);
}
/**
*后序遍历
*/
public void postorder(Visitor<E> visitor){
if (visitor==null)
return;
inorder(root,visitor);
}
public void postorder(Node<E> ndoe,Visitor<E> visitor){
if (ndoe==null || visitor.stop)
return;
postorder(ndoe.left,visitor);
postorder(ndoe.right,visitor);
// System.out.print(ndoe.element+" ");
//拿到stop 如果为ture 如何终止递归?
if (visitor.stop)
return;
visitor.stop=visitor.visit(ndoe.element);
}
//层序遍历
public void levelOrder(Visitor<E> visitor){
if (root==null ||visitor==null)
return;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
// System.out.print(node.element+" ");
if(visitor.visit(node.element))
return;
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
}
}
//------------------------------
/**
*前序遍历打印 树状二叉树
*/
public String toString(){
StringBuilder sb=new StringBuilder();
toStirng(root,sb,"");
return sb.toString();
}
private void toStirng(Node<E> node, StringBuilder sb,String prefix){
if (node==null)
return;
sb.append(prefix).append(node.element).append("\n");
toStirng(node.left,sb,prefix+"L---");
toStirng(node.right,sb,prefix+"R---");
}
//---------------------------------------------------
/**
*计算二叉树的高度(其实就是计算根节点的高度)
* 这个方法获取某一个节点的高度---传入根节点
*/
public int height1(){
return height1(root);
}
private int height1(Node<E> node){
if (node==null)
return 0;
return 1+Math.max(height1(node.left),height1(node.right));
}
//---------------------------------------------------------------------
/**
*层序遍历求树的高度
*思路:
* 1:每访问完一层就执行++操作
* 2:关键点是 如何确定 这一层 访问完了
* 首先得确定 你这一层有多少个 有个规律
*
*每当一层中最后一个元素出队--那么队列长度就是下一层元素个数
* 当 levelSize为0时,意味着这一层访问完了 队列长度就是下一层元素个数
*/
public int height(){
if (root==null)
return 0;
int height=0;
//存储每一层元素数量
int levelSize=1;//根节点 默认一个
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
levelSize--;
//入队
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
//当 levelSize为0时,意味着这一层访问完了 队列长度就是下一层元素个数
if (levelSize==0){
levelSize=queue.size();
height++;
}
}
return height;
}
//-----------------------------------------------------------
/**
* 层序遍历应用:
*判断一颗树是否为完全二叉树
*/
public boolean isComplete(){
if (root==null) return false;
boolean leaf=false;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()) {
Node<E> node= queue.poll();
//从第一个叶子节点开始 后面都是叶子节点
if (leaf && !isLeaf(node))
return false;
if (node.left!=null)
queue.offer(node.left);
else if(node.right!=null){
//node.left==null && node.right!=null
return false;
}
if (node.right!=null)
queue.offer(node.right);
else {
//node.left==null && node.right==null
//node.left!=null && node.right==null
leaf=true;
}
}
return true;
}
public boolean isLeaf(Node<E> node){
return node.left==null && node.right==null;
}
//----------------------------------------------
/**
*前驱节点
*/
private Node<E> predecessor(Node<E> node){
if (node==null)
return null;
Node<E> p=node.left;
//前驱节点在左子树当中(left.right.right.right...)
if (p!=null){
while (p.right!=null){
p=p.right;
}
return p;
}
//从父节点/祖父节点中寻找前驱节点
//发现是父节点的左子树的时候就一直往上找/父节点不为空
while (node.parent!=null && node==node.parent.left){
node=node.parent;
}
//退出循环的两种情况
//a:node.parent==null
//b:node==node.parent.right
return node.parent;
}
/**
*后继节点
*/
private Node<E> successor(Node<E> node){
if (node==null)
return null;
Node<E> p=node.right;
//前驱节点在左子树当中(right.left.left.left..)
if (p!=null){
while (p.left!=null){
p=p.left;
}
return p;
}
//从父节点/祖父节点中寻找后继节点
//发现是父节点的右子树子树的时候就一直往上找/父节点不为空
while (node.parent!=null && node==node.parent.right){
node=node.parent;
}
//退出循环的两种情况
//a:node.parent==null
//b:node==node.parent.left
return node.parent;
}
//--------------------------------------------------------------------
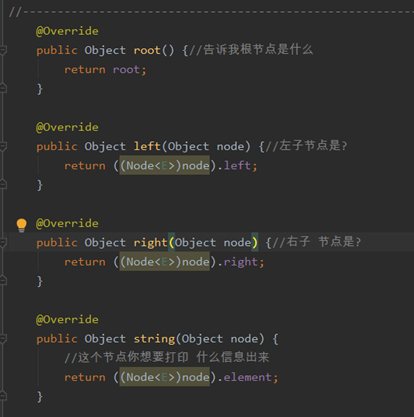
@Override
public Object root() {//告诉我根节点是什么
return root;
}
@Override
public Object left(Object node) {//左子节点是?
return ((Node<E>)node).left;
}
@Override
public Object right(Object node) {//右子 节点是?
return ((Node<E>)node).right;
}
@Override
public Object string(Object node) {
//这个节点你想要打印 什么信息出来
return ((Node<E>)node).element;
}
}
代码重构:
就是上面的最终代码里面,可以把共有的方法写到二叉树中,然后让二叉搜素树去继承。当然节点这些private就需要改成protected,否则外部子类访问不到。
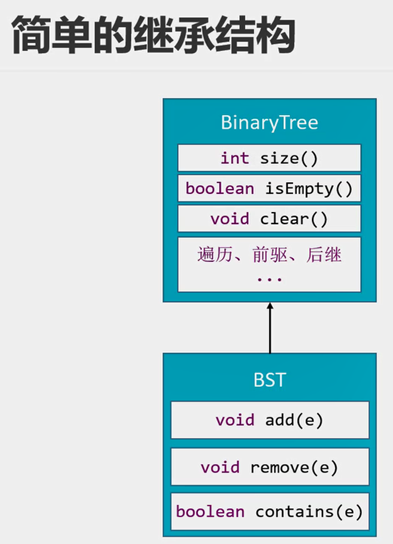
重构后二叉树代码
package tree;
import tree.printer.BinaryTreeInfo;
import java.util.LinkedList;
import java.util.Queue;
public class BinaryTree<E> implements BinaryTreeInfo {
protected int size;
/**
* 定义一个根节点--这样就可以通过一个根节点 就可以找到所以的节点了
*/
protected Node<E> root;
public int size(){
return size;
}
public boolean isEmpty(){
return size==0;
}
public void clear(){
root=null;
size=0;
}
//前驱,后继节点
//----------------------------------------------
/**
*前驱节点
*/
protected Node<E> predecessor(Node<E> node){
if (node==null)
return null;
Node<E> p=node.left;
//前驱节点在左子树当中(left.right.right.right...)
if (p!=null){
while (p.right!=null){
p=p.right;
}
return p;
}
//从父节点/祖父节点中寻找前驱节点
//发现是父节点的左子树的时候就一直往上找/父节点不为空
while (node.parent!=null && node==node.parent.left){
node=node.parent;
}
//退出循环的两种情况
//a:node.parent==null
//b:node==node.parent.right
return node.parent;
}
/**
*后继节点
*/
protected Node<E> successor(Node<E> node){
if (node==null)
return null;
Node<E> p=node.right;
//前驱节点在左子树当中(right.left.left.left..)
if (p!=null){
while (p.left!=null){
p=p.left;
}
return p;
}
//从父节点/祖父节点中寻找后继节点
//发现是父节点的右子树子树的时候就一直往上找/父节点不为空
while (node.parent!=null && node==node.parent.right){
node=node.parent;
}
//退出循环的两种情况
//a:node.parent==null
//b:node==node.parent.left
return node.parent;
}
//------------------------------------------
//---------遍历
/**
*前序遍历
*/
public void preorderTraversal(){
preorderTraversal(root);
}
private void preorderTraversal(Node<E> node){
if (node==null)
return;
System.out.print(node.element+" ");
preorderTraversal(node.left);
preorderTraversal(node.right);
}
/**
*中序遍历
*/
public void inorderTraversal(){
inorderTraversal(root);
}
public void inorderTraversal(Node<E> ndoe){
if (ndoe==null)
return;
inorderTraversal(ndoe.left);
System.out.print(ndoe.element+" ");
inorderTraversal(ndoe.right);
}
/**
*后序遍历
*/
public void postorderTraversal(){
postorderTraversal(root);
}
public void postorderTraversal(Node<E> ndoe){
if (ndoe==null)
return;
postorderTraversal(ndoe.left);
postorderTraversal(ndoe.right);
System.out.print(ndoe.element+" ");
}
/**
*层序遍历
*/
public void levelOrderTraverlsal(){
if (root==null)
return;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
System.out.print(node.element+" ");
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
}
}
//---------------------------------------
//根据自己的需求遍历元素
public static abstract class Visitor<E>{
/**
* 接口变为抽象类 是为了存储 stop
* 每一次调用都是唯一的 每次创建对象是唯一的
*/
boolean stop;
/**
*如果返回true 就代表停止遍历
* 如果返回 false 继续遍历
*/
abstract boolean visit(E element);
}
//前序遍历
public void preorder(BST.Visitor<E> visitor){
if (visitor==null)
return;
preorder(root,visitor);
}
//前序遍历 只需要判断一次
private void preorder(Node<E> node, BST.Visitor<E> visitor){
if (node==null || visitor.stop)
return;
// System.out.print(node.element+" ");
visitor.stop=visitor.visit(node.element);
preorder(node.left,visitor);
preorder(node.right,visitor);
}
/**
*中序遍历
*/
public void inorder(BST.Visitor<E> visitor){
if (visitor==null)
return;
inorder(root,visitor);
}
public void inorder(Node<E> ndoe, BST.Visitor<E> visitor){
if (ndoe==null || visitor.stop)
return;
inorder(ndoe.left,visitor);
// System.out.print(ndoe.element+" ");
//拿到stop 如果为ture 如何终止递归?
if (visitor.stop)
return;
visitor.stop=visitor.visit(ndoe.element);
inorder(ndoe.right,visitor);
}
/**
*后序遍历
*/
public void postorder(BST.Visitor<E> visitor){
if (visitor==null)
return;
inorder(root,visitor);
}
public void postorder(Node<E> ndoe, BST.Visitor<E> visitor){
if (ndoe==null || visitor.stop)
return;
postorder(ndoe.left,visitor);
postorder(ndoe.right,visitor);
// System.out.print(ndoe.element+" ");
//拿到stop 如果为ture 如何终止递归?
if (visitor.stop)
return;
visitor.stop=visitor.visit(ndoe.element);
}
//层序遍历
public void levelOrder(BST.Visitor<E> visitor){
if (root==null ||visitor==null)
return;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
// System.out.print(node.element+" ");
if(visitor.visit(node.element))
return;
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
}
}
//定义节点
//----------------------------------------------
protected static class Node<E>{
E element;
Node<E> left;
Node<E> right;
Node<E> parent;
/**
* 添加一个节点--除了根节点外一定有父节点
* 左子树,右子树不一定有。
*/
public Node(E element, Node<E> parent){
this.element=element;
this.parent=parent;
}
}
//---------------------------------------------------
/**
*计算二叉树的高度(其实就是计算根节点的高度)
* 这个方法获取某一个节点的高度---传入根节点
*/
public int height1(){
return height1(root);
}
private int height1(Node<E> node){
if (node==null)
return 0;
return 1+Math.max(height1(node.left),height1(node.right));
}
//---------------------------------------------------------------------
/**
*层序遍历求树的高度
*思路:
* 1:每访问完一层就执行++操作
* 2:关键点是 如何确定 这一层 访问完了
* 首先得确定 你这一层有多少个 有个规律
*
*每当一层中最后一个元素出队--那么队列长度就是下一层元素个数
* 当 levelSize为0时,意味着这一层访问完了 队列长度就是下一层元素个数
*/
public int height(){
if (root==null)
return 0;
int height=0;
//存储每一层元素数量
int levelSize=1;//根节点 默认一个
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()){
//头节点出队
Node<E> node=queue.poll();
levelSize--;
//入队
if (node.left!=null){
queue.offer(node.left);
}
if (node.right!=null){
queue.offer(node.right);
}
//当 levelSize为0时,意味着这一层访问完了 队列长度就是下一层元素个数
if (levelSize==0){
levelSize=queue.size();
height++;
}
}
return height;
}
//------------------------------------
/**
* 层序遍历应用:
*判断一颗树是否为完全二叉树
*/
public boolean isComplete(){
if (root==null) return false;
boolean leaf=false;
//JDK中的队列用的是LinkedList
Queue<Node<E>> queue=new LinkedList<>();
//入队 offer
queue.offer(root);
while (!queue.isEmpty()) {
Node<E> node= queue.poll();
//从第一个叶子节点开始 后面都是叶子节点
if (leaf && !isLeaf(node))
return false;
if (node.left!=null)
queue.offer(node.left);
else if(node.right!=null){
//node.left==null && node.right!=null
return false;
}
if (node.right!=null)
queue.offer(node.right);
else {
//node.left==null && node.right==null
//node.left!=null && node.right==null
leaf=true;
}
}
return true;
}
public boolean isLeaf(Node<E> node){
return node.left==null && node.right==null;
}
//----------------------------------------------------
/**
*前序遍历打印 树状二叉树
*/
public String toString(){
StringBuilder sb=new StringBuilder();
toStirng(root,sb,"");
return sb.toString();
}
private void toStirng(Node<E> node, StringBuilder sb,String prefix){
if (node==null)
return;
sb.append(prefix).append(node.element).append("\n");
toStirng(node.left,sb,prefix+"L---");
toStirng(node.right,sb,prefix+"R---");
}
//-------------------------------------------------------------------
//下面是打印二叉树图像的设置 不用管
//------------------------------------------
@Override
public Object root() {//告诉我根节点是什么
return root;
}
@Override
public Object left(Object node) {//左子节点是?
return ((Node<E>)node).left;
}
@Override
public Object right(Object node) {//右子 节点是?
return ((Node<E>)node).right;
}
@Override
public Object string(Object node) {
//这个节点你想要打印 什么信息出来
return ((Node<E>)node).element;
}
}
重构后二叉搜索树的代码
package tree;
import java.util.Comparator;
public class BST<E> extends BinaryTree {
private Comparator<E> comparator;
public BST(){
this(null);
}
public BST(Comparator<E> comparator){
this.comparator=comparator;
}
public void add(E element){
//添加元素不能为空 首先判断一下
elementNotNullCheck(element);
//添加第一个节点
if (root==null){
root=new Node<>(element,null);
size++;
return;
}
/**
* 如果添加的不是第一个节点
*1:找到父节点--通过父节点找到它下面节点的数据
* 所以下面赋值 root--从根节点开始找
*/
Node<E> parent=root;
Node<E> node=root;
int cmp=0;//为啥定义到外面 因为待会儿 需要用到这个数据
//找到插入位置的父节点
while (node!=null){
cmp=compare(element,node.element);
parent=node;
if (cmp>0){//e1>e2
node=node.right;
}else if (cmp<0){//e1<e2
node=node.left;
}
/**
* 值相同 两种做法
* 1:啥也不干 直接return
* 2:建议覆盖原来的值---
* 因为如果是基本的类型都无所谓,但是如果是自定义类型等,它的比较规则是其中的莫一项/多项,
* 如果相同按理是应该加入,所以覆盖,具体情况而定吧,根据需求。
*/
else {//相同的情况 覆盖原来的值
node.element=element;
return;
}
}
//看看插入到父节点的哪个位置
Node<E> newNode=new Node<>(element,parent);
if (cmp>0){
parent.right=newNode;
}else {
parent.left=newNode;
}
size++;
}
/**
*删除这个元素--相当于删除某个节点
* 先根据这个元素--找到节点对象--node(E element)
* 然后--remove(Node<E> node)--删除这个节点
*/
//根据元素--找到对应的节点
private Node<E> node(E element){
Node<E> node=root;
while (node!=null){
int cmp=compare(element,node.element);
if (cmp==0)
return node;
if (cmp>0){
node=node.right;
}else{
node=node.left;
}
}
return null;
}
public void remove(E element){
remove(node(element));
}
public boolean hasTwoChildren(Node<E> node){
return node.left!=null && node.right!=null;
}
private void remove(Node<E> node){
if (node==null)
return;
size--;
/**
* 删除度为2的节点
* a:找到该节点的 前驱/后继节点
* b:用 前驱/后继节点的值 覆盖度为2节点的值
* c:删除后继/前驱节点
*/
if (hasTwoChildren(node)){
//找到后继节点(找前驱节点也可以)
Node<E> s=successor(node);
//用后继节点的值覆盖度为二的值
node.element=s.element;
//删除后继节点
//将度为2的节点指向后继节点,那么就只需要删除后继节点就可以了。
node=s;
}
//删除node节点(注意此时已经指向了s):s它的度必为0或1
//如果是度为1需要找到它的子节点
Node<E> replacement=node.left!=null?node.left:node.right;
if (replacement!=null){//node是度为1的节点
//更改parent
replacement.parent=node.parent;
//更改parent的left,right的指向
if (node.parent==null){//node是度为1的节点并且是根节点
root=replacement;
//这里不需要这一步 replacement.parent=null
//因为更改parent那一步已经完成了这一步。
}
else if (node==node.parent.left){
node.parent.left=replacement;
}else if (node==node.parent.right){
node.parent.right=replacement;
}
}else if(node.parent==null) {//node是叶子节点并且是根节点
root=null;
}else {//node是叶子节点,但不是根节点
if (node==node.parent.right){
node.parent.right=null;
}else{//node==node.parent.left
node.parent.left=null;
}
}
}
public boolean contains(E element){
return node(element)!=null;
}
/**
* 返回值
*e1=e2---0
*e1>e2--大于0
* e1<e2--小于0
*/
private int compare(E e1,E e2){
//不为空---使用传入的比较器
if (comparator!=null){
//根据外面传入比较器的规则 进行比较
return comparator.compare(e1,e2);
}
//为空--采用默认的比较方式--
return ((Comparable<E>)e1).compareTo(e2);
}
//由于添加元素的element不能为空---需要添加一个方法检测
private void elementNotNullCheck(E element){
if (element==null)
throw new IllegalArgumentException("element must not be null");
}
}
二叉树作业
◼ 二叉树的前序遍历: https://leetcode-cn.com/problems/binary-tree-preorder-traversal/ (递归+迭代)
◼ 二叉树的中序遍历: https://leetcode-cn.com/problems/binary-tree-inorder-traversal/ (递归+迭代)
◼ 二叉树的后序遍历: https://leetcode-cn.com/problems/binary-tree-postorder-traversal/ (递归+迭代)
◼ 二叉树的层次遍历: https://leetcode-cn.com/problems/binary-tree-level-order-traversal/ (迭代)
◼ 二叉树的最大深度: https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/ (递归+迭代)
◼ 二叉树的层次遍历II: https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/
◼ 二叉树最大宽度:https://leetcode-cn.com/problems/maximum-width-of-binary-tree/
◼ N叉树的前序遍历: https://leetcode-cn.com/problems/n-ary-tree-preorder-traversal/
◼ N叉树的后序遍历: https://leetcode-cn.com/problems/n-ary-tree-postorder-traversal/
◼ N叉树的最大深度: https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
◼ 二叉树展开为链表
https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list/
◼ 从中序与后序遍历序列构造二叉树
https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
◼ 从前序与中序遍历序列构造二叉树
https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
◼ 根据前序和后序遍历构造二叉树
https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/
◼ 对称二叉树
https://leetcode-cn.com/problems/symmetric-tree/
二叉树应用练习
翻转二叉树

Letcode:2226
思路:遍历二叉树 将每一个节点的左右子树进行交换
前序遍历
先访问自己进行交换 然后访问左右子树
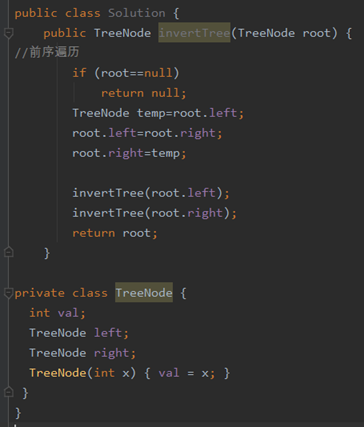
后序遍历
先访问它的左右 然后再访问自己 然后进行交换
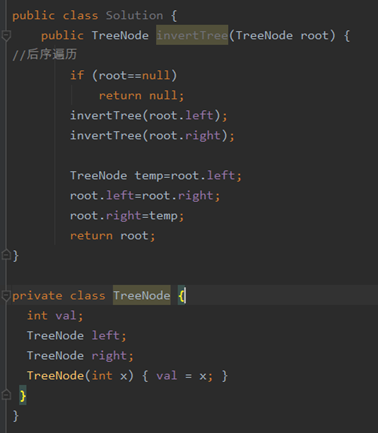
中序遍历
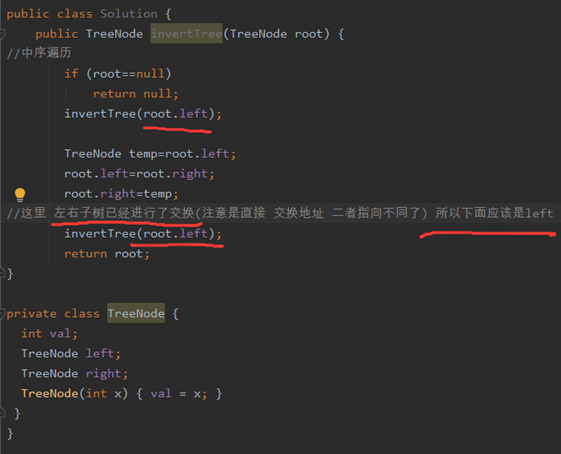
层序遍历
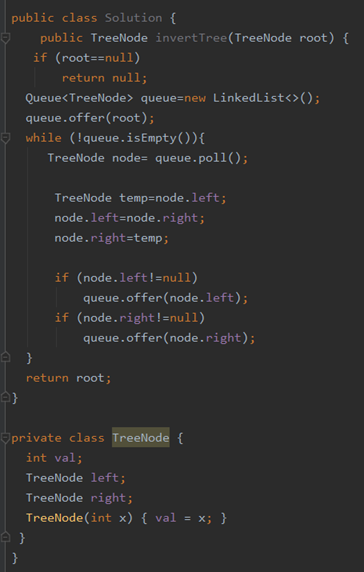
总结:就是遍历 将每个节点的左右子树进行交换


 浙公网安备 33010602011771号
浙公网安备 33010602011771号