实验3
task1
#include <stdio.h> char score_to_grade(int score); int main() { int score; char grade; while(scanf("%d", &score) != EOF) { grade = score_to_grade(score); printf("分数: %d, 等级: %c\n\n", score, grade); } return 0; } char score_to_grade(int score) { char ans; switch(score/10) { case 10: case 9: ans = 'A'; break; case 8: ans = 'B'; break; case 7: ans = 'C'; break; case 6: ans = 'D'; break; default: ans = 'E'; } return ans; }
result:

q1:对成绩除以10得到整数结果,并判断相应的等级,且输出等级
形参类型:int整型;返回值类型:char字符型、
q2:第一,赋值等级时使用了双引号,所以是字符串类型,那么不能赋给char这个变量,应修改为使用单引号;
第二,各个case后面没有添加break会导致一直往下执行,直到default,应修改为在每个case后面添加break
task2
#include <stdio.h> int sum_digits(int n); int main() { int n; int ans; while(printf("Enter n: "), scanf("%d", &n) != EOF) { ans = sum_digits(n); printf("n = %d, ans = %d\n\n", n, ans); } return 0; } int sum_digits(int n) { int ans = 0; while(n != 0) { ans += n % 10; n /= 10; } return ans; }
result:

换成第二种写法运行结果如下
q1:函数sum_digits的作用是不断取n这个数字上每一位的数字并求和
q2:可以实现同样输出,结果如task2.2图。
原定义方法是迭代,对原输入结果n进行不断地升位取数字并相加
第二种方法是递归,设置n<10时为出口,对原输入结果不断简化直至找到出口并得到结果
task3
#include <stdio.h> int power(int x, int n); int main() { int x, n; int ans; while(printf("Enter x and n: "), scanf("%d%d", &x, &n) != EOF) { ans = power(x, n); printf("n = %d, ans = %d\n\n", n, ans); } return 0; } int power(int x, int n) { int t; if(n == 0) return 1; else if(n % 2) return x * power(x, n-1); else { t = power(x, n/2); return t*t; } }
result:

q1:输入x和n并计算x的n次方,返回结果
q2:是递归函数
出口是n=0时返回结果为1,以此为基底;
若n为奇数时,则将n向前推一位,得到返回结果是向前推一位的幂运算结果×x;
若n为偶数时,则将n除以2推进并将结果平方得到返回结果;
以上流程均可在得到一次结果后继续选择分支进行流程,直至达到出口即n=0。
数学公式(如果是这么写的话)
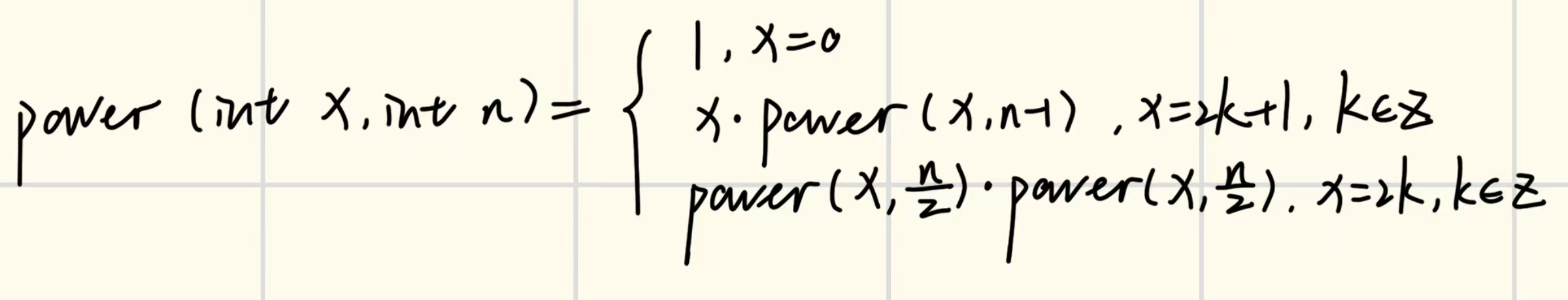
task4
#include <stdio.h> int is_prime(int n); int main() { printf("100以内的孪生素数:\n"); int i; int count = 0; for (i=2;i<=98;i++) { if (is_prime(i) && is_prime(i+2)) { printf("%d, %d\n",i,i+2); count++; } } printf("100以内的孪生素数共有%d个\n", count); return 0; } int is_prime(int n) { if (n <= 1) return 0; if (n == 2) return 1; if (n % 2 == 0) return 0; int i; for (i= 3; i * i <= n; i += 2) { if (n % i == 0) { return 0; } } return 1; }
result:

task5
Edit1:迭代
#include <stdio.h> int func(int n, int m); int main() { int n, m; int ans; while(scanf("%d%d", &n, &m) != EOF) { ans = func(n, m); printf("n = %d, m = %d, ans = %d\n\n", n, m, ans); } return 0; } int func(int n,int m){ int up=1, down_1 = 1,down_2 = 1; int ans = 1; int i,j,k; for(i=1;i<=n;i++) up*=i; for(j=1;j<= m;j++) down_1*=j; for(k=1;k<=(n-m);k++) down_2*=k; ans = up/(down_1*down_2); return ans; }
result:
Edit2:递归
#include <stdio.h> int func(int n, int m); int main() { int n, m; int ans; while(scanf("%d%d", &n, &m) != EOF) { ans = func(n, m); printf("n = %d, m = %d, ans = %d\n\n", n, m, ans); } return 0; } int func(int n,int m){ if (m>n) return 0; else if (m == n||m == 0) return 1; else return func(n-1,m)+func(n-1,m-1); }
result:
task6
#include <stdio.h> int gcd(int a,int b,int c); int main() { int a, b, c; int ans; while(scanf("%d%d%d", &a, &b, &c) != EOF) { ans = gcd(a, b, c); printf("最大公约数: %d\n\n", ans); } return 0; } int gcd(int a,int b,int c){ int min = a; int i; if(b < min) min = b; if(c < min) min = c; for(i = min;i>=i;i--){ if(a % i == 0 && b % i == 0 && c % i == 0) return i; } }
result:

task7
#include <stdio.h> #include <stdlib.h> void print_charman(int n); int main() { int n; printf("Enter n: "); scanf("%d", &n); print_charman(n); return 0; } void print_charman(int n){ int i,j,k; for (i=1;i<=n;++i) { for (j=0;j<=i-1;j++){ printf("\t"); } for (k =2*n-2*i+1;k>0;k--){ printf(" \t O ");} printf("\n"); for (j=0;j<=i-1;j++){ printf("\t"); } for (k=2*n-2*i+1;k>0;k--){ printf("\t<H>");} printf("\n"); for (j=0;j<=i-1;j++) { printf("\t"); } for (k=2*n-2*i+1;k>0;k--) { printf("\tI I");} printf("\n"); } }
result:
conclusions:
1.注意使用单引号或双引号来引用字符的时候,这些符号会决定它是字符还是字符串,进而引发赋值是否符合形式的问题,可能引发报错,需要注意(这点与python不同)
2.在写迭代和递归两种思路的代码时候,很明显可以看出迭代是直接抽象出一个普适规律然后用代码表现出来;但递归则是需要确定一个出口,再从出口往后推进其他情况的处理,向后推的时候严重依赖之前的成果,所以需要理清楚每一项与前一项之间的关系,不过这种的思路在写代码的时候会更简单
3.递归的出口真的很重要很重要,写递归思路的时候需要考虑清楚特殊情况以及出口
4.还是排版的问题,排版决定可读性,可读性决定报错的时候自查的速度()
that's all!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号