19-10-29-Z

%%%ZZYY

只是因为是Z才模一下的。

ZJ一下：

考试T1写了三张纸但是它死了。

T2T3暴力叕写跪了。

考试一定一定不能不严密，少推两个交点是要命的啊。

就因为叕叕少开龙龙见祖宗了。

如果考试能推出一个点就试试推两个，有两个就试试推三个，别一直觉得自己能A……

……话说我对拍半天愣是没卡掉。

TJTime:

T1

给大家讲讲简单高考数学。

首先上来就可以得出一句话题意。

给定$a,b,S$求当$ax+by=S$时$|x|+|y|$的最小值

求前式的特解还是很容易的辣，直接$exgcd$硬上即可。

问题出在如何将后式的最小值计算出。

记特解值为$x',y'$，当$a,b$互质时一定有$x=x'+kb,y=y'-kb(k \in \mathbb{Z})$

若不互质则左右同除$gcd$。

于是转化为求$$\min\{|x'+kb|+|y'-ka|\}$$

高考数学告诉我们，遇到绝对值要想办法去绝对值。

于是可以分$4$种情况:（等于可包含于下面任一种情况）

$$
\begin{array}{cc}
\begin{cases}
x'+kb<0\\
y'-ka<0
\end{cases}&
\begin{cases}
x'+kb<0\\
y'-ka>0
\end{cases}\\
\begin{cases}
x'+kb>0\\
y'-ka<0
\end{cases}&
\begin{cases}
x'+kb>0\\
y'-ka>0
\end{cases}\\
\end{array}
$$

那么这四种情况下的直线可以表示为：

$$
\begin{cases}
t=(a-b)k-x'-y'\\
t=(-a-b)k-x'+y'\\
t=(a+b)k+x'-y'\\
t=(-a+b)k+x'+y'
\end{cases}
$$
从高考数学的严密性出发，下面应该再判断$-\frac{x'}{b}$与$\frac{y'}{a}$的大小关系然后计算交点。

所以图像的可能形状如下：

 

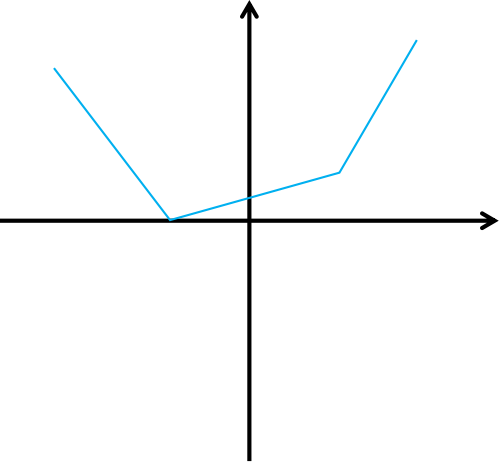
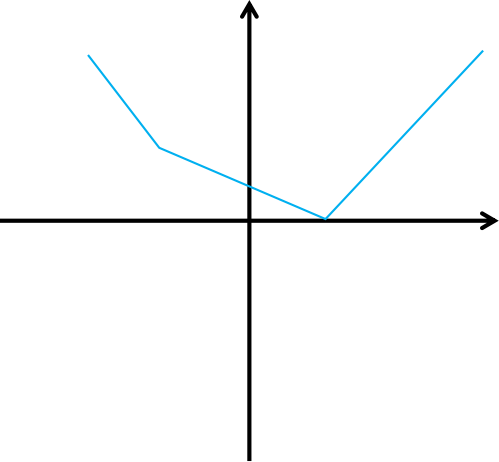
但是还有一种，考试时没有考虑到，因为我们不能保证图像连续（另外可能的情况暂不列出），于是，如下：

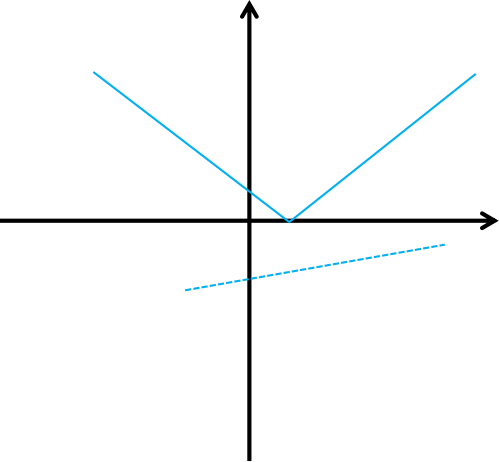
但是在本题中，并不需要此种做法，我们可以直接计算四条直线之间的交点，理论上可以有$C_4^2$种方案，但实际计算得出的结果并没有那么多。

即$t \in \{\frac{y}{a},-\frac{x}{b},\frac{x-y}{-a-b},\frac{x+y}{a-b}\}$

终于……

#include <iostream>
#include <cstring>
#include <cstdio>
#define N 111111
#define LL long long

using namespace std;

LL a,b,arr[N],nn;
LL ans;
inline LL Abs(LL x){
	return x<0?-x:x;
}
LL exgcd(LL &x,LL &y,LL _a,LL _b){
	if(_b==0){
		x=1;
		y=0;
		return _a;
	}
	LL ret=exgcd(x,y,_b,_a%_b);
	LL z=x;
	x=y;
	y=z-_a/_b*y;
	return ret;
}
LL getans(LL x,LL y,LL t){
	return min(Abs(x+t*b)+Abs(y-t*a),
		   min(Abs(x+(t-1)*b)+Abs(y-(t-1)*a),
			   Abs(x+(t+1)*b)+Abs(y-(t+1)*a)));
}
int main(){
	LL x,y,gcn;
	scanf("%lld%lld%lld",&nn,&a,&b);
	gcn=exgcd(x,y,a,b);
	for(int i=1;i<=nn;i++)
		scanf("%lld",arr+i);
	a/=gcn,b/=gcn;
	for(int i=1;i<=nn;i++){
		if(arr[i]%gcn!=0){
			puts("-1");
			return 0;
		}
		LL xd=x*arr[i]/gcn,yd=y*arr[i]/gcn,t;
		LL nans[10];
		t=-xd/b;
		nans[0]=getans(xd,yd,t);

		t=yd/a;
		nans[1]=getans(xd,yd,t);

		t=(xd+yd)/(a-b);
		nans[2]=getans(xd,yd,t);

		t=(xd-yd)/(-a-b);
		nans[3]=getans(xd,yd,t);
		
		ans+=min(min(nans[0],nans[1]),min(nans[2],nans[3]));
	}
	cout<<ans<<endl;
}

其实还可以三分直接过。

T2

我去做DZKP了。

T3

做了。

发现要求每两个特殊点之间的距离，

第一想法是$Floyd$（多源）

但是显然T

下面想如何将单源最短路搞成多源。

记录当下的点从哪些点转移过来，最后扫边更新答案就行了。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#define LL long long
#define N 222222
#define pre first
#define len second

using namespace std;

typedef pair<LL,LL> pll;
template <typename Tp>
class Myqueue{
	Tp A[N*10];
	int f,b;
	public:
	Myqueue(){f=b=0;}
	void clear(){f=b=0;}
	void push(const Tp k){A[b++]=k;}
	void pop(){f++;}
	bool empty(){return f==b;}
	Tp front(){return A[f];}
	void pour(){
		for(int i=f;i<b;i++){
			cout<<A[i]<<" ";
		}
		cout<<endl;
	}
};
struct Edge{
	int f,t,next;
	LL v;
}rs[2*N];
vector  <int>sp;
Myqueue <int> q;
pll dis[N];
int pn,edn,spn,
	fl[N],cnt=0;
LL ans[N];
bool inq[N];

void add(int f,int t,int v){
	rs[cnt].f=f;
	rs[cnt].t=t;
	rs[cnt].next=fl[f];
	rs[cnt].v=v;
	fl[f]=cnt++;
}
void SPFA(){
	for(int i=1;i<=pn;i++)
		dis[i]=make_pair(0,1e15);
	for(int i=0;i<sp.size();i++){
		dis[sp[i]].pre=sp[i];
		dis[sp[i]].len=0;
		q.push(sp[i]);
		inq[sp[i]]=1;
	}
	while(!q.empty()){
		int f=q.front();q.pop();
//		q.pour();
		for(int i=fl[f];i!=-1;i=rs[i].next){
			int t=rs[i].t;
			if(dis[t].len>dis[f].len+rs[i].v){
				dis[t]=make_pair(dis[f].pre,dis[f].len+rs[i].v);
				if(!inq[t]){
					q.push(t);
					inq[t]=1;
				}
			}
		}
		inq[f]=0;
	}
/*	for(int i=1;i<=pn;i++){
		cout<<i<<" "<<dis[i].len<<" "<<dis[i].pre<<endl;
	}*/
}
int main(){
	int a,b;
	LL v;
	cin.sync_with_stdio(false);
	memset(ans,0x7f,sizeof ans);
	memset(fl,-1,sizeof fl);
	cin>>pn>>edn>>spn;
	for(int i=1;i<=spn;i++){
		cin>>a;
		sp.push_back(a);
	}
	for(int i=1;i<=edn;i++){
		cin>>a>>b>>v;
		add(a,b,v);
		add(b,a,v);
	}
	SPFA();
	for(int i=0;i<cnt;i++){
		int af=dis[rs[i].f].pre,
			bf=dis[rs[i].t].pre;
//		cout<<af<<" "<<bf<<endl;
		if(af!=bf){
			LL val=dis[rs[i].t].len+dis[rs[i].f].len+rs[i].v;
			ans[af]=min(ans[af],val);
			ans[bf]=min(ans[bf],val);
		}
	}
	for(int i=0;i<spn;i++)
		printf("%lld ",ans[sp[i]]);
	puts("");
}